地球物理勘探中几种二维插值方法的误差分析

王兆国，程顺有，刘 财

1.西北大学大陆动力学教育部重点实验室，西安 710069

2.西北大学地质学系，西安 710069

3.吉林大学地球探测科学与技术学院，长春 130026

0 引言

在地球物理工作以及地质勘探中，为确保可实现性和可操作性，往往对研究区进行离散观测，然后对离散的数据经过一系列处理形成时间或空间上的离散数据体，在离散数据体的图像呈现上常采用二维插值方法进行处理。二维插值方法已经应用于许多领域，如：葛志广等[1]用不同的网格化方法对高精度磁法数据进行了分析；张美根等[2]和曾闽山等[3]分别就非规则地震数据和海量散点地震数据进行了网格化研究；陈晓军等[4]对油藏数据进行了Voronoi网格化研究等。对于各种二维插值方法，如反距离加权插值法、克里金插值法、最小曲率法、改进的谢别德法、自然邻点插值法、最近邻点插值法、多元回归法、径向基函数法、线性插值三角网法、移动平均法、局部多项式插值和反插值法，在前人的研究中就其基本原理和效果图的对比都有过论述[5-11]。研究图件要反映整个研究区异常特征，但它是离散采样的结果，因此就形成了图件与真实情况差异问题，即误差问题。成像误差的影响因素包含3个方面的内容：一是地质体本身大小的影响；二是采样密度的影响；三是网格化插值方法的影响。此前的研究主要考虑选取不同插值方法的影响，但没有研究各种插值方法具体的误差问题，而对于采样密度影响几乎没有论述。

笔者主要针对采样密度和二维插值方法对成像的误差大小进行研究。为了确定其影响情况，模拟了2个重力异常场，然后通过不同的采样间距和网格化方法对模拟数据进行不同插值方法的插值，对比插值数值与真实值之间的误差，从而确定插值方法本身的精度情况。

1 插值方法的基本思想

网格化方法实质上是一种利用已知点值进行二维空间插值的方法，各种不同方法的主要区别在于利用的采样点范围的不同和已知点权重的不同。采样点范围的不同表现为全局插值和局部插值，而已知点权重的不同在于权重函数（基函数）的不同。由于多元回归法是一种趋势面作图法，局部多项式插值法也可以看作是局部趋势面法，即用一个曲面去拟合已知数据，可以采用不同幂次，主要用来区分区域场与局域场，因此方法本身就对精细的构造起到一种去除作用，笔者不再讨论。移动平均法，通过“窗”进行搜索，拟合程度对“窗”的大小非常依赖，“窗”选择不合适往往造成图的畸变，当采用不同采样间距时，主要是“窗”的选取问题，因此笔者也不再讨论。笔者主要讨论反距离加权插值法、克里金插值法、最小曲率法、改进的谢别德法、自然邻点法、最近邻点法、径向基函数法和线性插值三角网法：反距离加权法容易受到数据点集群的影响，计算结果中常出现孤立点数据明显高于周围数据点的现象；克里金法利用变差函数描述函数值的区域变化，不仅考虑了已知点对待插点的影响，而且考虑了已知点之间的相互影响，网格化精度效果的好坏，依赖于理论变差函数拟合的好坏；最小曲率法主要考虑曲面的光滑性，容易超出最大值和最小值的范畴；改进的谢别德法是对反距离加权法的改进，利用节点函数的二次曲面拟合值代替离散点值，提高了内插值精度和曲面光滑度，权函数只在局部起作用，并使用最小二乘法克服了反距离加权的“牛眼”缺点；自然邻点法是基于Voronoi结构的一类插值方法；最近邻点法假设任意网格点的属性值都用距离它最近位置点的属性值，更适合于变化不大且测量点密度大的情况；径向基函数法是多个数据插值方法组合的一种多形式网格化方法，具有很强的拟合数据点、产生光滑曲面的能力；线性插值的三角网法计算速度快，网格化结果不光滑，精度和效果较差，计算可能会出现不稳定。

反距离加权插值是利用平面上已知的一系列离散点，把离散点与插值点之间距离的倒数作为权重，进行插值[5-7]，公式如下：

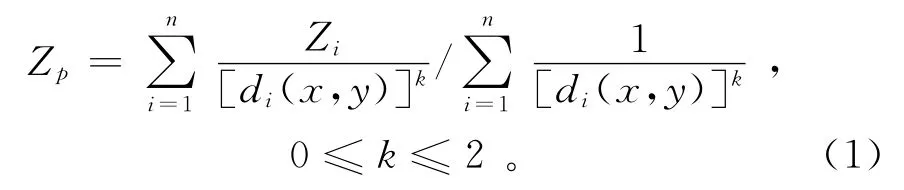
其中：di（x，y）＝，表示离散点（xi，yi）与插值点（xp，yp）间的距离；Zi是各离散点的属性值；Zp为插值点p的属性值。

改进的谢别德插值法是对反距离加权插值的改进，主要改进有2个方面：一是把权重函数由全局插值改为局部插值；二是引入节点函数代替离散点的属性值[5]，但权重依然采用距离的倒数。克里金插值法是一种对空间分布数据求最优、线性、无偏内插估计量的方法。它的优点在于不仅考虑了各已知数据点的空间相关性，而且在给出待估计点数值的同时，还能给出表示估计精度的方差。克里金方程组是在无偏性条件和估计方差最小条件下给出的[5-8]。最小曲率法构造具有最小曲率的曲面，使其穿过空间场的每一点，在尽量严格地尊重数据的同时，生成尽可能圆滑的曲面，最小曲率法主要考虑曲面的光滑性，因此插值容易超出最大和最小值的范畴[5]。自然邻点插值法是基于Voronoi结构的一类插值方法，其权重函数形式[5，12]为

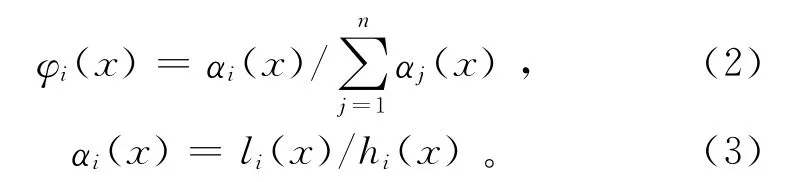
其中：li（x）是与节点关联的Voronoi边的长度；hi（x）是节点到插值点的垂直距离。

最近邻点插值法中隐含的假设是插值点的属性值使用距离它最近的节点属性值表示，区域变量平均属性形式[5]为

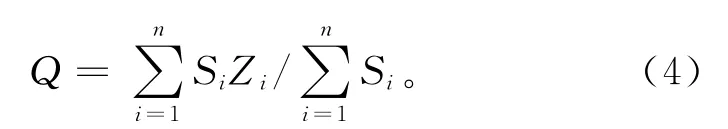
其中，Si是由所有网格点连线的垂直平分线切割成的多边形面积。

径向基函数法是多个数据插值方法的组合，其基函数由单变量函数构成，复二次基函数法被认为是其中最佳的。线性插值三角网法是基于delaunay三角网剖分的插值方法[13-14]，要保证2个前提：所有三角形的边不能相交；保证三角形最小内角和为最大。这2个条件保证尽可能避免生成小内角的长薄单元，使三角形能够接近等角或等边[15]。

2 模型选取与计算

为了研究不同采样间距和插值方法对成图误差的影响，首先确定一个简单的模型（模型一）：地质体为一长方体，上表面位于10km深度，下底面位于15km深度，水平2个方向长度相同，分别取0.5，2.0，4.0，6.0，8.0，10.0，15.0，20.0km 的长度，地质体在地表的投影中心为坐标原点。用如图1所示的模型，计算了不同地质体尺度（C）分别在0.5，1.0，2.5，4.0，5.0，8.0，10.0，20.0km 的 采样 间 距和不同插值方法下的绝对误差的均方根值（图2）。

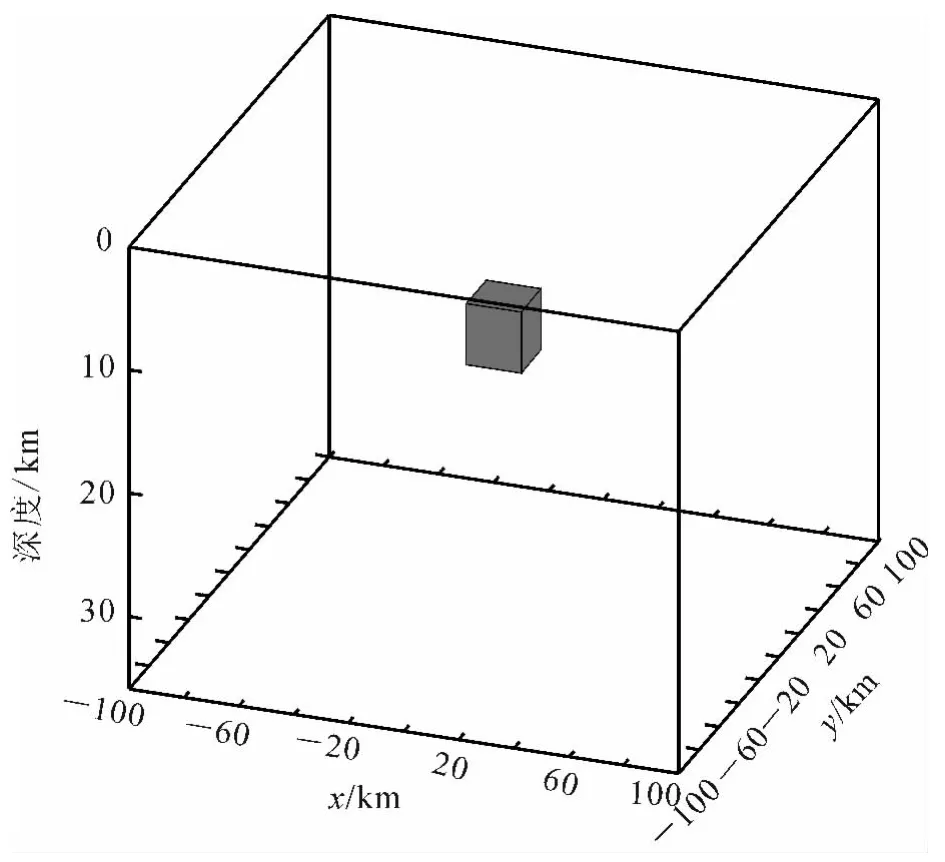
图1 模型一Fig.1 Model 1

从图2中可以看出：所有插值方法在相同地质体下，随着采样间距的增大，误差均方根值总体趋势是增大的，也就是采用小采样间距时地质体误差较小；所有方法在相同采样间距下，随着目标体的增大，误差均方根值总体是增大的，产生此现象的原因是大目标体产生的场的影响范围大，插值产生的误差的范围增大。

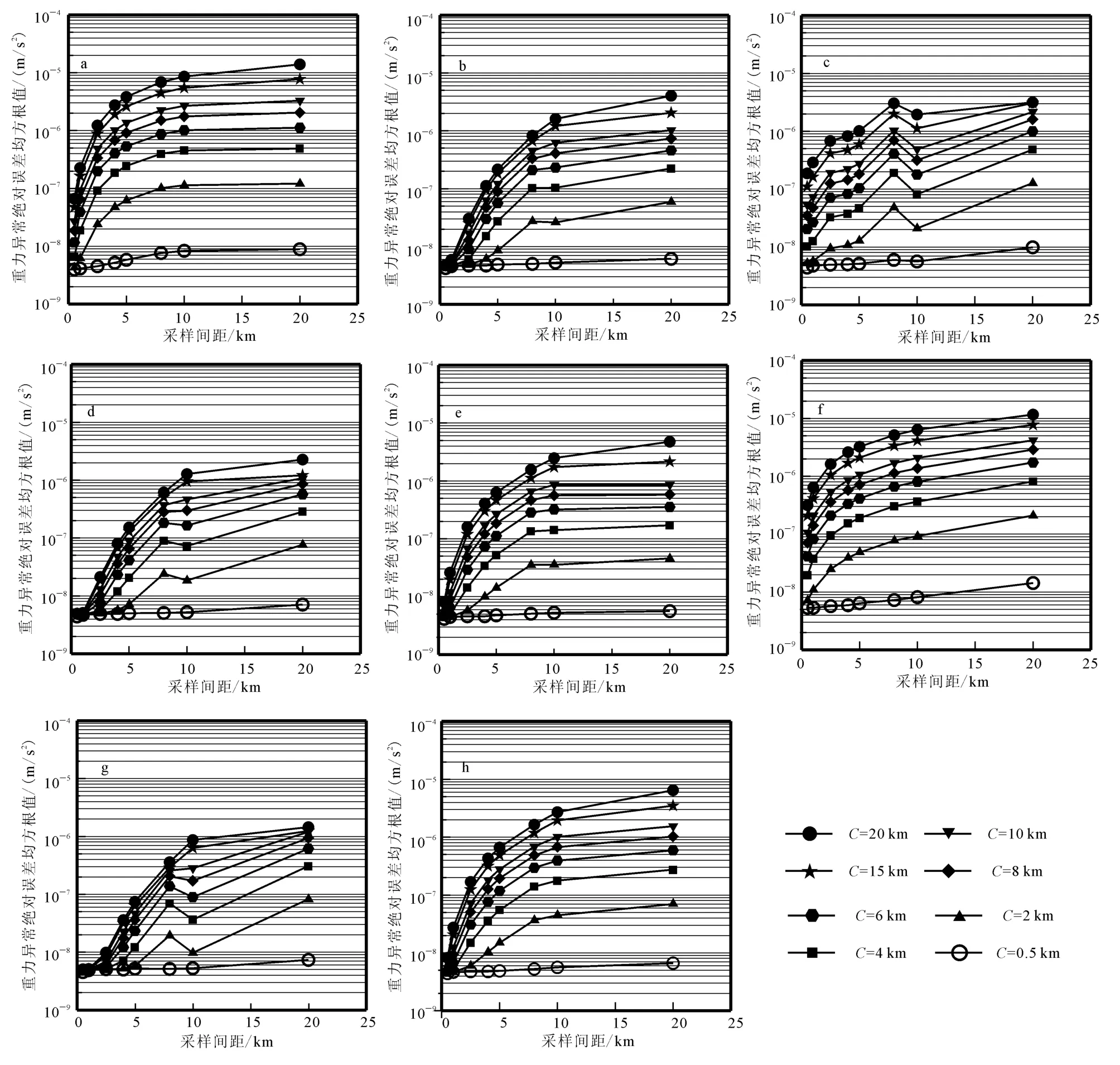
图2 模型一不同插值方法采样间距与地质体尺度关系的绝对误差均方根值曲线图Fig.2 Curve graph of absolute error mean square value of relationship of sampling spacing and geological body scale of different interpolation methods in model 1

为了进一步比较不同网格化方法误差的差异，选用一个更一般的重力模型（模型二，图3）：底部是2层正剩余密度层，被一正剩余密度和一负剩余密度的薄板状异常体所隔断；薄板状异常体的倾角为45°，两薄板异常体的宽度均为10km；左侧的2层地层厚度分别为5km和10km，上顶面位于10km深度，下底面位于25km深度；右侧2层地层厚度分别为5km和10km，上顶面位于15km深度，下底面位于30km深度。这些异常是作为整个区域的区域异常体，其在深度-x面上的投影如图3b所示。2层正剩余密度层上方在薄板状体两侧各有一长方体负剩余密度体，为了更好地研究局部异常的影响，在右侧的长方体负剩余密度体左侧，建立了3个正方体正剩余密度体。这些异常作为局部异常体，5个局部异常体的厚度均为5km，其在x-y面上的投影如图3c所示。模型二原始数据特征如图4所示，上部为立体图，下部为投影图。

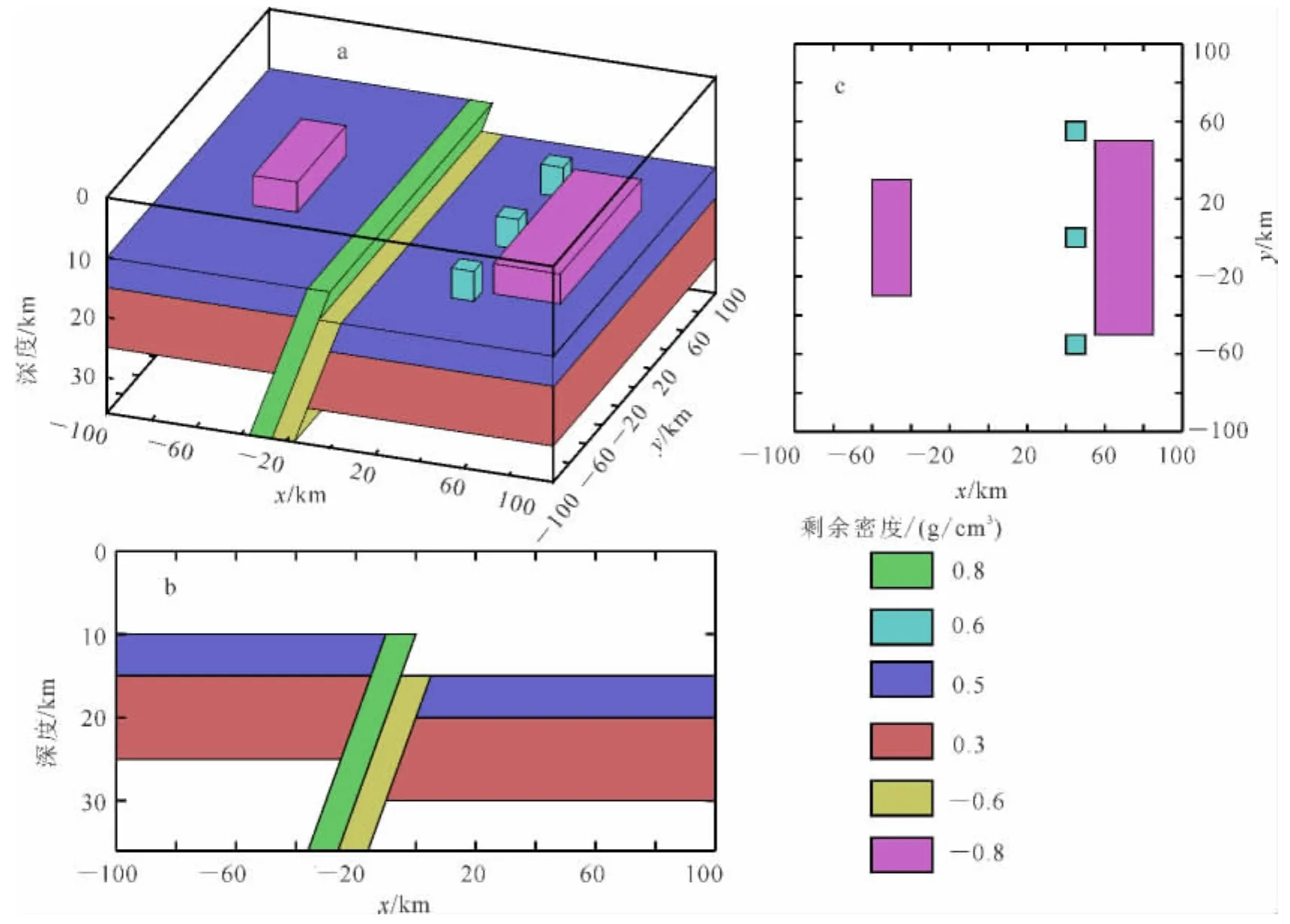
图3 模型二Fig.3 Model 2

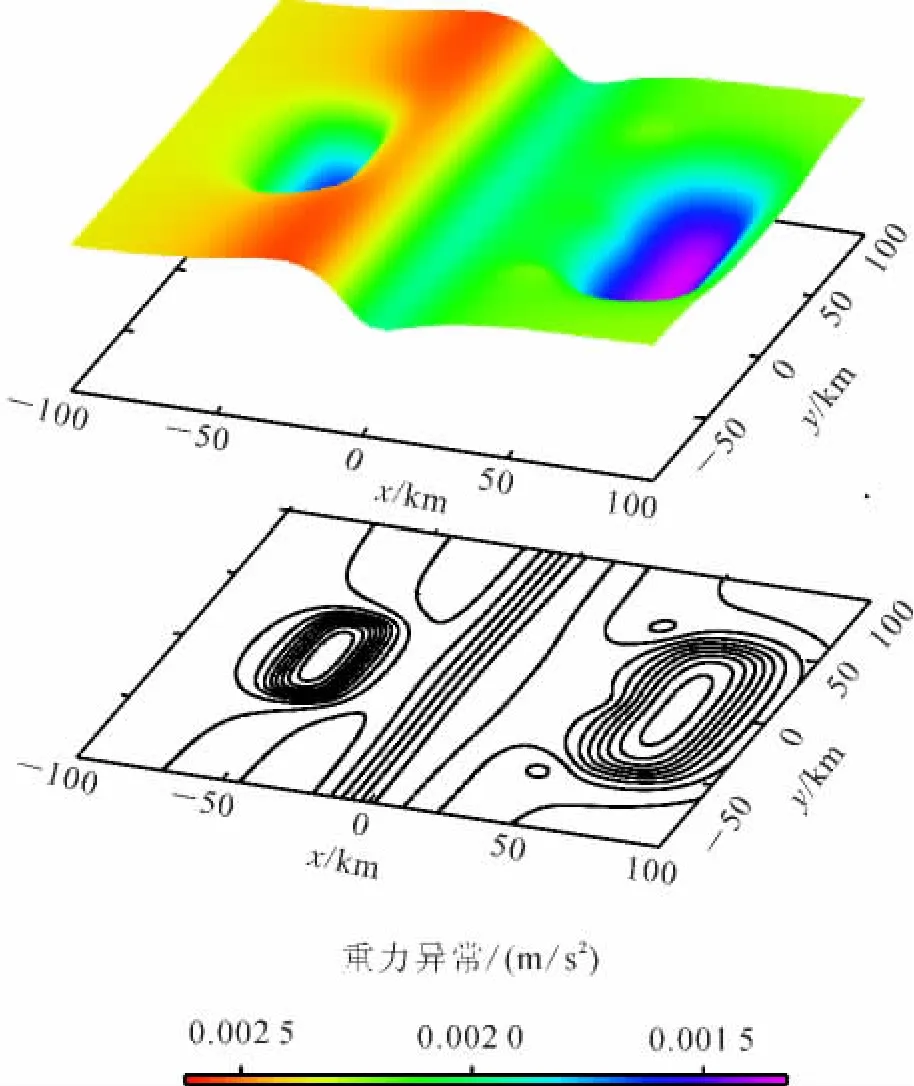
图4 模型二重力异常特征Fig.4 Characteristics of gravity anomaly of model 2

对于模型二，笔者采用不同的采样间距计算了不同网络化插值方法的误差大小，如表1所示。

对模型二，固定地质体尺度，采用不同的采样间距，计算不同插值方法的均方根值，来反映不同方法插值的好坏程度。由图5可以看出：径向基函数法在插值成图时误差最小，其次为改进的谢别德法和克里金插值法，自然邻点法和线性插值三角网法在图上的折线几乎重合，误差大小几乎相同，误差较大的为反距离加权插值法、最小曲率法和最近邻点法；当采样间距小于4km（最小异常地质体尺度）时，误差较大的后3种方法绝对误差均方根值由小到大的顺序是：反距离加权插值法、最近邻点法、最小曲率法；当采样间距大于4km时，这3种方法绝对误差均方根值由小到大的顺序是：最小曲率法、最近邻点法、反距离加权插值法。

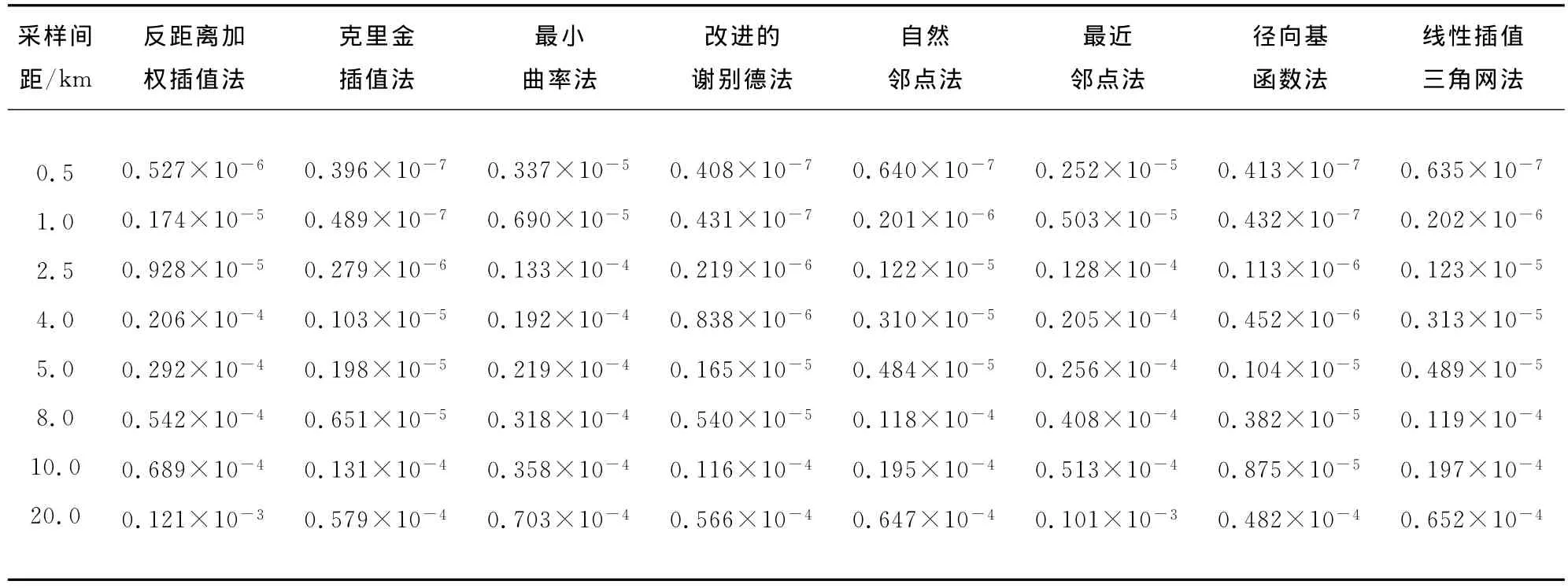
表1 模型二不同插值方法的绝对误差均方根值Table1 Absolute error root mean square values of different interpolation methods of model 2

图5 模型二不同插插方法的绝对误差均方根值曲线图Fig.5 Curve graph of absolute error mean square value of different interpolation methods of model 2

绝对误差均方根值反映了方法总体插值误差的大小，为了进一步观测插值时重力异常任何一个节点处的绝对误差，对模型二用采样间距为0.5km的插值节点的绝对误差来反映内部节点处的误差（图6）。从图6可以看出：径向基函数法（图6g）、改进的谢别德法（图6d）和克里金插值法（图6b），所有节点上误差几乎相同，绘图时对于地质体边界数据的影响最小；而自然邻点法（图6e）、线性插值三角网法（图6h）、反距离加权插值法（图6a）、最小曲率法（图6c），在局部地质体边上范围内绝对误差相对较大，对于绘图时地质体边界的影响大；而最近邻点法（图6f），出现局部异常体形态的明暗相间的灰度图，最暗（负）和最明（正）都意味着误差大，因此最近邻点法对绘图时误差影响大。

3 结论

1）对于同一插值方法而言，存在小间距绝对误差均方根值小于大间距绝对误差均方根值的关系。对不同的插值方法而言，当采样间距小于4.0km时，绝对误差均方根值由小到大的顺序是：径向基函数法、改进的谢别德法、克里金插值法、自然邻点法、反距离加权插值法、最近邻点法、最小曲率法，并且线性插值三角网法与自然邻点法具有几乎相同的数值；采样间距大于4.0km时，绝对误差均方根值由小到大的顺序是：径向基函数法、改进的谢别德法、克里金插值法、自然邻点法、最小曲率法、最近邻点法、反距离加权插值法，并且线性插值三角网法和自然邻点法具有几乎相同的数值。从绝对误差均方值看，径向基函数方法、改进的谢别德方法和克里金方法较小，其中径向基函数值绝对误差均方根值最小。

2）从节点处绝对误差值来看，径向基函数方法、克里金方法、改进的谢别德方法相对其他插值方法具有更小的误差，不存在局部误差较小或较大的情况，是相对较好的插值方法，并且径向基函数方法是最好的。

图6 模型二不同插值方法节点处绝对误差灰度图Fig.6 Grey-scale map of absolute error of nodes of different interpolation methods of model 2

（References）：

[1]葛志广，宋俊杰.高精度磁法数据网格化方法的选取[J].工程地球物理学报，2010，7（2）：169-172.Ge Zhiguang，Song Junjie.The Griding Methods of Selection About the Data of High-Precision Magnetic[J].Chinese Journal of Engineering Geophysic，2010，7（2）：169-172.

[2]张美根，乌达巴拉，王妙月.非规则网带断层地震数据的网格化[J].地球物理学进展，1999，14（1）：69-77.Zhang Meigen，Wudabala，Wang Miaoyue.Gridding of Inregular Seismic Data with Faults[J].Progress in Geophysics，1999，14（1）：69-77.

[3]曾闽山，侯岩松.海量地震数据网格化算法分析与研究[J].石油天然气学报：江汉石油学院学报，2006，28（2）：72-75.Zeng Minshan，Hou Yansong.The Analysis and Research on Gridding Algorithm for Massive Seismic Data[J].Jounral of Oil and Gas Technology：J JPI，2006，28（2）：72-75.

[4]陈晓军，陈伟，段永刚，等.油藏Voronoi网格化的研究[J].西南石油大学学报：自然科学版，2010，32（1）：121-124.Chen Xiaojun，Chen Wei，Duan Yonggang，et al.The Research on Reservoir Voronoi Grid[J].Journal of Southwest Petroleum University： Science ＆Technology Edition，2010，32（1）：121-124.

[5]陈欢欢，李星，丁文秀.Surfer 8.0等值线绘制中的十二种插值方法[J].工程地球物理学报，2007，4（1）：52-57.Chen Huanhuan，Li Xing，Ding Wenxiu.Twelve Kinds of Gridding Methods of Surfer 8.0in Isoline Drawing [J].Chinese Journal of Engineering Geophysics，2007，4（1）：52-57.

[6]蔡玉华.达里亚工区速度体建立中几种网格化方法的对比分析[J].石油物探，1995，34（4）：100-108.Cai Yuhua.Gridding Methods Used for Constructing Velocity Volume in Daliya：Comparative Analysis[J].Geophysical Prospecting for Petrol，1995，34（4）：100-108.

[7]刘兆平，杨进，武炜.地球物理数据网格化方法的选取[J].物探与化探，2010，34（1）：93-97.Liu Zhaoping，Yang Jin，Wu Wei.The Choice of Gridding Methods for Geophysical Data [J].Geophysical and Geochemical Exploration，2010，34（1）：93-97.

[8]郭良辉，孟小红，郭志宏，等.地球物理不规则分布数据的空间网格化法[J].物探与化探，2005，29（5）：438-442.Guo Lianghui，Meng Xiaohong，Guo Zhihong，et al.Gridding Methods of Geophysical Irregular Data in Space Domain [J].Geophysical and Geochemical Exploration，2005，29（5）：438-442.

[9]程红杰，胡祥云，田米玛，等.地震数据网格化方法研究[J].工程地球物理学报，2006，3（1）：28-32.Cheng Hongjie，Hu Xiangyun，Tian Mima，et al.The Study of Seismic Data Gridding Methods[J].Chinese Journal of Engineering Geophysics，2006，3（1）：28-32.

[10]郭良辉，孟小红，郭志宏，等.反插值法实现地球物理数据快速网格化[J].地球物理学进展，2005，20（3）：671-676.Guo Lianghui，Meng Xiaohong，Guo Zhihong，et al.Fast Gridding of Geophysical Data with Inverse Interpolation[J].Progress in Geophysics，2005，20（3）：671-676.

[11]马英莲，彭树宏，钱静.基于Surfer软件的两种数据插值方法研究[J].测绘通报，2010（8）：54-57.Ma Yinglian，Peng Shuhong，Qian Jing.A Study of Two Data Interpolation Methods Based on Surfer Software[J].Bulletin of Surveying and Mapping，2010（8）：54-57.

[12]王兆清，冯伟.高度不规则网格多边形单元的有理函数插值格式[J].固体力学学报，2005，26（2）：199-202.Wang Zhaoqing，Feng Wei.Rational Function Interpolation Scheme of Polygonal Elements Based on Highly Irregular Grids[J].Acta Mechanica Solida Sinica，2005，26（2）：199-202.

[13]Green P J，Sibson R.Computing Direchlet Tesselations in the Plane[J].Computer Journal，1978，21（2）：168-173.

[14]Watson D F.Computing the N-Dimensional Delaunay Tessellation with Application to Voronoi Polytopes[J].Computer Journal，1981，24（2）：167-172.

[15]张岭，郝天珧.基于Delaunay剖分的二维非规则重力建模及重力计算[J].地球物理学报，2006，49（3）：877-884.Zhang Ling，Hao Tianyao.2-D Irregular Gravity Modeling and Computation of Gravity Based on Delaunay Triangulation [J].Chinese Journal of Geophysics，2006，49（3）：877-884.