改进的蚁群算法及其在南岭地区花岗岩侵入体探测中的应用

刘 双，陈国雄，刘天佑

1.中国地质大学地球物理与空间信息学院，武汉 430074

2.中国地质大学地质过程与矿产国家重点实验室，武汉 430074

0 引言

南岭地区地质构造复杂，矿产资源丰富，是世界上研究燕山期大陆成矿体系和花岗岩成岩成矿理论最典型的地区之一。研究南岭地区花岗岩侵入体的侵位特征，对研究区深部控矿规律、深部成矿模式的认识以及深部成矿预测意义重大。而重磁勘探是研究该区区域深部构造、花岗岩侵位以及成矿预测的重要手段，前人做了很多相关工作。秦葆瑚［1－3］指出，湘南一些大型－特大型内生多金属矿田不但具有明显的特殊地质条件，而且在区域重、磁场上有明显的异常反映；并对水口山、东坡、瑶岗仙、黄沙坪4个大型多金属矿田的区域重磁异常特征进行了总结。李少莲［4］在研究湘南地区隐伏构造中指出了壳型和幔型花岗岩类的重磁场特征：壳型花岗岩类重力异常规模较大，航磁异常为正负伴生；而幔型花岗岩类通常处于重力梯度带或者重力梯度带交叉部位，航磁ΔT异常规模较小。段利华［5］利用湘桂粤赣区域重力垂向二次导数、重力区域场垂向二次导数以及航磁局部场分析浅部和深部的花岗岩带信息，推断出区内的隐伏花岗岩体信息，认为地幔凹区是成矿的有利地区，矿体的形成与隐伏岩体及其形态相关。朱自强等［6］利用神经网络反推算法，对千里山岩体及其邻区进行三维重磁反演，给出了岩体的空间形态及侵位，并预测找矿靶区。饶家荣等［7］根据南岭地区地质地球物理资料，研究了南岭中段主要深断裂和隐伏花岗岩带的分布特征，指出大义山－郴州－大宝山北西向隐伏构造带控制着大型－超大型矿床，并提出以地球物理和地球化学资料为基础，创建具有“重低磁高”或重磁变异特征的半隐伏－隐伏花岗岩带的构造岩浆系列矿床成矿模式，指导和开展南岭地区深部找矿。

蚁群智能优化算法（ant colony optimization，ACO）是继模拟退火算法、遗传算法、人工神经网络等启发式随机搜索算法以后的又一种启发式算法。该算法在控制与决策问题中取得了较好的效果，例如旅行商问题（TSP）［8－13］，背包问题（QAP）［14－20］，指派问题（JSP）［21］等经典组合优化问题。组合优化问题是在离散空间寻求最优解，然而，地球物理反问题是多维连续目标函数的优化，解空间比组合优化问题大很多，从而增加了蚁群算法在地球物理反演应用中的难度。近年来，有学者将蚁群算法应用于地震反演和地震解释，如陈双全等［22］用蚁群算法进行地震数据AVO反演，严哲等［23］用蚁群算法进行地震剖面断层识别和层速度反演；而将ACO应用于地球物理资料特别是重磁资料反演的实例还很少。Yuan等［24］在进行地球物理数据的群智能最优化反演时，采用连续参数离散化的策略，将ACO应用于地震记录及重力异常的参数化反演，在与拟牛顿法、Levenberg－Marquardt（L－M）、模拟退火算法（SA）及遗传算法（GA）反演结果的比较中，ACO显示出更好的并行性、鲁棒性及收敛性。笔者改进了传统组合优化问题中蚁群算法的映射模式，使得蚁群算法更适用于重磁资料的反演；然后根据两条1∶2 000高精度重力剖面数据，用蚁群算法探测千里山岩体和九嶷山岩体的延深、赋存形态，以期为研究南岭地区花岗岩侵入模式和多金属成矿规律提供参考。

1 重磁反演蚁群优化算法

1.1 蚁群行为

蚂蚁属于群居昆虫，个体行为极其简单，而群体行为却相当复杂。相互协作的一群蚂蚁很容易找到从蚁巢到食物源的最短路径，而单个蚂蚁则不能。人们通过大量的研究发现，蚂蚁个体之间是通过在其所经过的路上留下一种称之为“信息素”的物质来进行信息传递的［8－9］。随后的蚂蚁遇到信息素时，不仅能检测出该物质的存在及多少，而且可根据信息素的浓度来选择前进方向。同时，该物质随着时间的推移会逐渐挥发，于是路径的长短及该路径上通过蚂蚁的多少就对残留信息素的强度产生不同的影响，反过来信息素的强弱又指导着其他蚂蚁的行动方向。因此，某一路径上走过的蚂蚁越多，则后来者选择该路径的概率就越大。这就构成了蚂蚁群体行为表现出的一种信息正反馈现象，蚂蚁个体之间就是通过这种信息交流搜索最优路径的。

1.2 重磁最优化反演目标函数

重磁资料最优化反演的目标函数φ由数据约束φd和模型约束φm两部分组成［25－26］，即

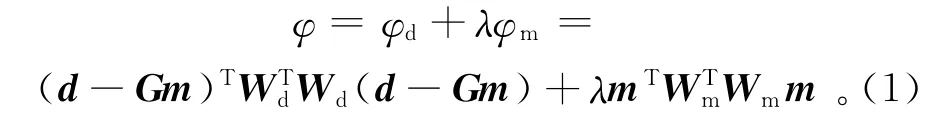
式中：λ为正则化参数；d＝（d1，d2，…，dm）为观测数据矢量；m＝（m1，m2，…，mn）为模型参数矢量，m和n分别为观测数据个数和模型参数个数；G为敏感度矩阵；为观测数据权重矩阵。对观测数据进行加权，若观测数据含均值为0的高斯白噪声，且相互独立［25－26］，则

式中：σ为观测数据噪声的标准差；I为单位矩阵。由于重磁异常幅值随测点到场源的距离增大而急剧衰减，若不对模型进行加权约束，磁性或密度的分布将集中分布于地表，出现“趋肤效应”。为抵消重磁异常急剧衰减的影响，需对模型进行深度加权［25－26］，即

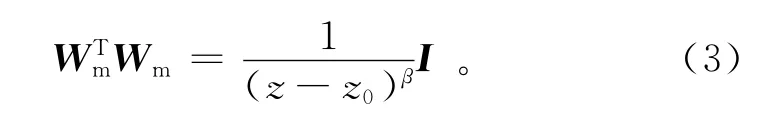
式中：z为单元体深度；z0是与深度有关的常数；β为与重磁异常随深度的衰减速率有关的常数。Li和 Oldenburg［25－26］进行3D重力数据反演时，设β＝2.0；进行3D磁力数据反演时，设β＝3.0。

1.3 重磁反演蚁群优化算法

蚁群最优化算法首先应用于求解组合优化问题（COPs），如旅行商问题（TSP）等。然而，对于重磁资料反演则是多维的连续的目标函数优化问题，解空间维数比COPs大得多，增加了最优化问题的难度。目标函数优化问题与TSP的相互对比如表1所示。

表1 重磁反演中目标函数优化问题与TSP优化问题的对比Table 1 Comparison of optimization to potential field data inversion and TSP

对式（1）目标函数进行蚁群算法最优化时，首先需将模型参数离散化［27－29］。在模型参数mi的取值范围内，将其划分为Ni个节点（i＝1，2，…，n），将每个模型参数看成1层，共计n层，个节点，代表TSP中的个“城市”（图1）。划分节点时，可以不必进行等分，且每一层的划分数量和参数范围也可以不一样。但是，为了使最优化问题简化，通常在每个模型参数的取值范围内进行N等分点，且每个模型参数的等分数量相同，因此共计n层n×N个节点。N的数量决定了最优化反演的精度：N越大，反演精度越高，但反演的计算量就越大；反之，N越小，反演的精度就越低，反演计算的计算量就越小。

初始时刻，将M只蚂蚁随机地放在m1的N个节点上。搜索开始后，蚂蚁按照转移概率

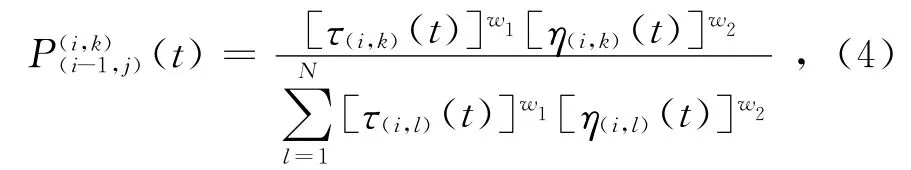
从（i－1，j）节点转移至（i，k）节点（2≤i≤n，1≤j≤N，1≤k≤N）。其中：τ（i，k）（t）为蚂蚁在t时刻节点（i，k）的信息素残留总量；η（i，k）（t）为蚂蚁在t时刻节点（i，k）的启发信息；w1、w2分别表示信息素和启发信息的权重。每只蚂蚁从第1层m1开始，层层转移，一直达到最后一层mn。则第s只蚂蚁经过的路径就对应一个解ms，可计算出对应的目标函数值φs。所有蚂蚁完成遍历后，更新节点（i，j）的信息素为

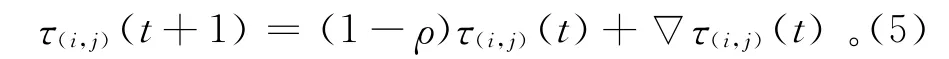
其中：ρ∈（0，1），称为挥发度；▽τ（i，j）（t）为所有蚂蚁在第t次遍历在节点（i，j）残留的信息素。挥发度避免了系统信息素的无节制积累，同时使得蚁群系统有机会弱化旧的信息，突出新的信息。单个节点的信息数残留量为所有蚂蚁在该节点残留的信息素之和，即

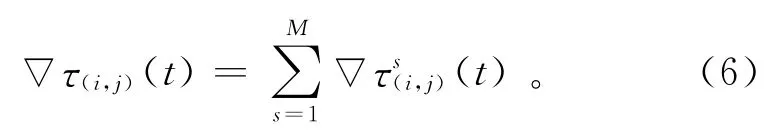
蚂蚁信息素残留量的取值极为重要，影响到反演的收敛速度和优化能力。在TSP最优化问题中，Dorigo等［8－9，30－31］提出 3 种模型，分别是 ant－cycle，ant－density和ant－quantity模型。其中，应用最广泛的ant－cycle模型定义为

其中：Q是一个常量，用来表示蚂蚁完成一次完整的路径搜索后释放的信息素总量，该值对搜索结果没有影响；Ls是第s只蚂蚁的总花费，它等于第s只蚂蚁经过各段路径上所需花费的总和，即Ls＝式中，li为第i段线路行走单位里程的费用为第s只蚂蚁经过的第i段线路的路程。antcycle说明，如果蚂蚁的路径总花费越高，那么其在单位路径上所释放的信息素浓度就越低，反之，残留的信息数浓度就越高。

蚁群系统的搜索机理说明，如果模型ms对应的目标函数φs越小，那么蚂蚁在经过路径上残留的信息素就越多，从而指导其他蚂蚁的搜索。当蚁群系统完成一次遍历后，更新节点信息素，开始下一次搜索，蚁群系统重新回到第一层，开始新的搜索，直到超过εs的蚂蚁遍历在同一条路径为止（0＜εs≤1，为收敛系数）。最终，蚁群系统将趋于同一条最短的路径，对应的最优解为m＊。

当蚁群系统收敛至同一路径以后，搜索基本停滞。若此时反演结果不能满足要求，则可以逐步缩小剖分范围，在解的临域

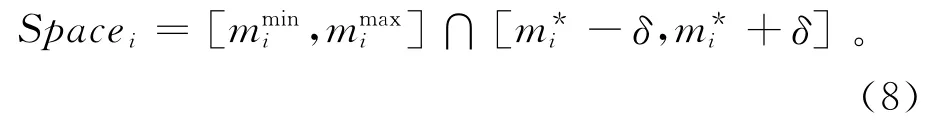
内进行重新剖分，重建解空间，并进行新一次的蚁群搜索，直到观测数据拟合误差小于ε为止（ε为收敛的拟合误差）。δ为临域半径，

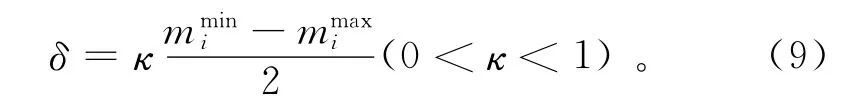
式中：为模型参数mi的最优解；，分别为模型参数mi的最小值和最大值；κ为与缩小剖分范围速度的系数。蚁群算法的流程图如图2所示。

2 重磁反演蚁群优化算法改进

本次对蚁群算法的改进在于目标函数与信息素之间的映射函数。尽管式（7）ant－cycle模型成功应用于 TSP、QAP和JSP等组合优化问题［8－9，30］，但是它在重磁资料反演中的应用效果还不好。重磁反演问题与TSP不同，重磁反演的解空间是通过连续域参数离散化得到的，而TSP本身就是由各个城市组成的离散化解空间；因此，TSP的解空间比重磁反演问题的解空间小得多，前者蚁群系统更容易搜索到最优解。在TSP中应用的ant－cycle模型寻优能力不强，没有实时更好地突出蚂蚁个体（即各个解）之间的差异，蚁群系统容易搜索到一个局部最优解，导致搜索过程过早停滞。由于蚁群系统搜索停滞，陷入局部极值，即使增加迭代次数或改变反演参数，也难从实质上提高收敛的速度和反演的精度。

图1 蚁群算法最优化目标函数示意图Fig.1 Diagram of ACO optimizing objective function

笔者认为，当蚁群系统完成一次遍历后，有必要对此次蚁群系统的搜索结果进行统计和评估。根据本次蚁群系统的搜索结果，合理计算信息素残留量，进而引导蚁群的下一步搜索；这样势必会增加算法的稳定性和收敛速度等。对蚁群系统搜素结果的统计，最主要是计算每只蚂蚁对应的目标函数值，所以对蚁群系统的统计就是对所有蚂蚁对应的目标函数值的统计。因此，笔者提出新的映射模型。新的映射模型为Gauss函数形式，称为Gauss模型，即

式中：μ（φ）和σ（φ）是整个蚁群系统目标函数的均值和方差；A为与信息素总量有关的常数，该常数对搜索结果没有影响。该式对每次搜索的结果进行数理统计，根据统计的目标函数分布，计算对应的信息素增量，突出了蚂蚁个体之间的差异，有利于加快收敛的速度，寻找全局最优解。

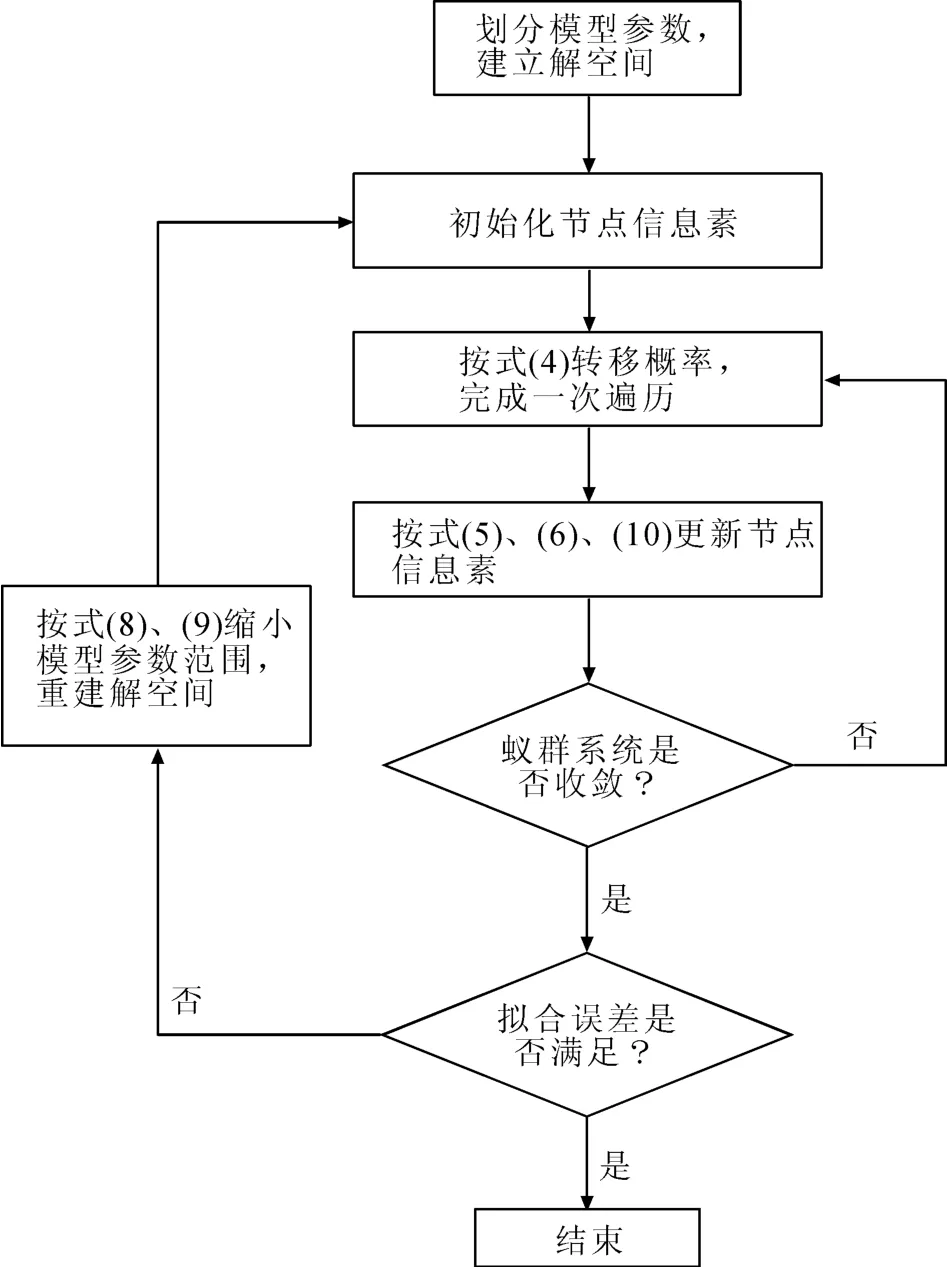
图2 蚁群算法最优化目标函数流程图Fig.2 Flowchart of ACO optimizing objective function

图3是二维矩形截面棱柱体模型磁异常的Gauss模型和ant－cycle模型蚁群算法反演结果。两者蚂蚁数量、节点层数、挥发系数等反演参数均是相同的。反演时，将1 000m×500m的介质范围划分为40×20＝800个网格单元，即模型参数的个数为800。将模型参数剖分为0和1两等分（0代表无磁性，1代表有磁性），因此共有2 800种可能的解。两者的蚂蚁数量为200，挥发系数为0.7；正则化参数（λ）也相同，均为103。由于Gauss模型和antcycle模型反演的初始模型是随机生成的，如果蚂蚁数量、等分数量相同，则随机生成的初始模型也是相同的。虽然两者控制信息素总量的常数不同（A＝1，Q＝107），但它们只控制蚁群系统的信息素总量，不会影响转移概率，所以对反演的结果不会产生影响。由图3可知，Gauss模型的反演结果比antcycle模型反演结果要好。前者磁性单元的聚集程度高，分辨率高，形状、边界与理论模型吻合很好；后者磁性单元分布较散，反演的磁性体分布和理论模型差别较大。

图4和表2是Gauss模型和ant－cycle模型反演的收敛过程对比。由图4、表2可知，Gauss模型的反演效率比ant－cycle模型高。Gauss模型目标函数下降快，收敛稳定；而ant－cycle模型目标函数下降缓慢，收敛速度慢。前者迭代97次收敛，耗时314s，拟合观测数据的相对误差达到2.0%；而后者迭代1 000次仍没收敛，耗时4 052s，拟合观测数据的相对误差为18.0%，反演的效率比Gauss模型低很多。这充分说明改进的Gauss模型比传统的antcycle模型效果好，这说明了算法改善的有效性。

3 理论试算

笔者设计两组磁性体模型来检验ACO算法的效果，分别是单个二度矩形截面棱柱体模型和组合二度板状体组成的向斜模型。两组磁性体单元的磁化强度M＝100A/m，磁化倾角I＝45°，测线方位角为0°。地面观测资料不含噪声，剖面长度为1 000 m，点距为20m，观测点数为51。矩形截面棱柱体模型ACO反演的正则化参数为103，向斜模型ACO反演的正则化参数为5×102。

3.1 单个模型

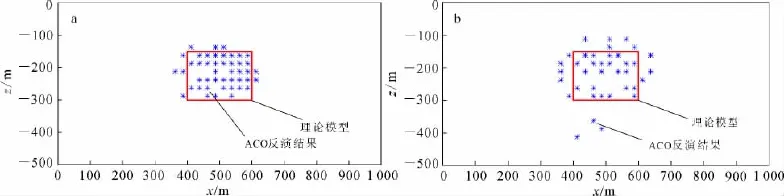
图3 Gauss模型和ant－cycle模型反演结果对比Fig.3 Comparisons of inversion results using Gauss system and ant－cycle system

图5是矩形截面棱柱体模型ACO反演的迭代收敛过程和反演结果。初始时刻，剖面的磁性分布是随机的、任意的（图5a）；随着蚁群系统的搜索，磁性单元的分布逐渐收拢，并与真实模型逐渐接近（图5b、c、d）；当经过97次搜索后，收敛停止，反演终止（图5e）。反演结果与真实模型非常接近，反演效果很好。

图4 Gauss模型和ant－cycl模型的收敛过程对比Fig.4 Comparisons of convergence processes using Gauss system and ant－cycle system

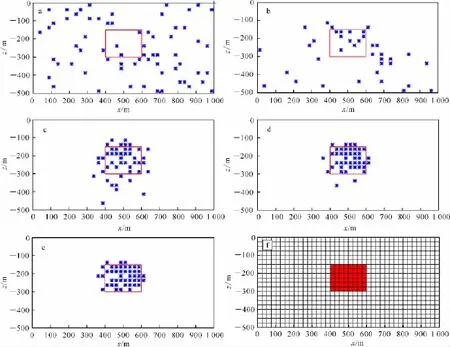
图5 二维矩形截面棱柱体模型蚁群算法反演结果Fig.5 ACO inversion results for synthetic two－dimensional rectangular prism model

表2 Gauss模型和ant－cycle模型反演结果对比Table 2 Comparison of inversion results of Gauss system and ant－cycle system

3.2 组合模型

图6是板状体组成的向斜模型ACO反演的迭代收敛过程和反演结果。同单个矩形截面棱柱体模型的反演类似，初始时刻，剖面的磁性分布是随机的、任意的（图6a）；随着蚁群系统的搜索，磁性单元的分布逐渐收拢，并与真实模型逐渐接近（图6b、c、d）；当经过191次搜索后，收敛停止，反演终止（图6e）。反演结果与真实模型非常接近，反演效果很好。

4 南岭花岗岩侵入体构造探测

4.1 地质与地球物理概况

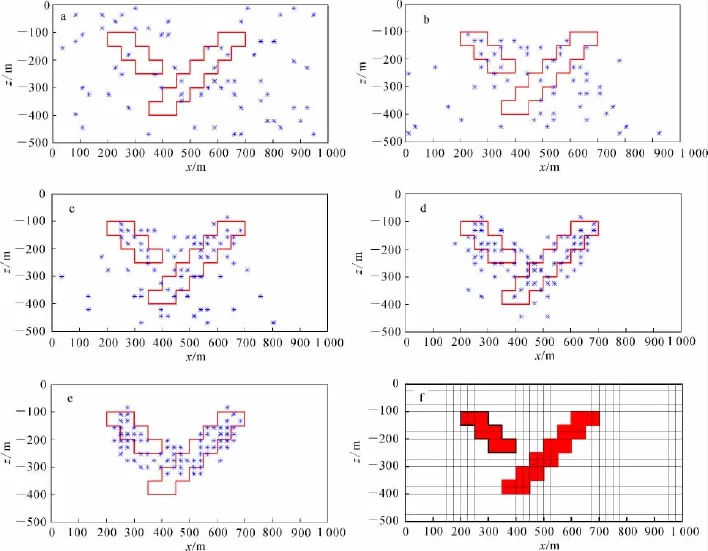
图6 二维向斜模型体模型蚁群算法反演结果Fig.6 ACO inversion results for synthetic two－dimensional syncline model

南岭地区在构造上横跨华夏板块与扬子板块，位于华南陆块构造岩浆活动带，历经多期次构造－岩浆－成矿作用，区内广泛发育着各种花岗岩和其他岩浆岩，是我国重要的金属矿成矿带之一，钨、锡、铜、铅、锌等许多内生金属矿床与花岗岩有密切关系。花岗岩密度较低，侵入到沉积地层中表现为负异常特征。根据前人所做的物性统计工作［7］得知，区内岩石密度分布有如下特征：1）碳酸盐岩密度大于砂页岩密度，灰岩平均密度为2.70g/cm3，页岩平均密度为2.53g/cm3；大理岩化灰岩、白云岩密度值为2.73～2.75g/cm3；矽卡岩平均值密度为3.27 g/cm3。2）浅源重熔型花岗岩密度常见值为2.6g/cm3，比一般围岩低，剩余密度为－0.05～－0.10g/cm3；而深源同熔型花岗岩其密度常见值为2.72g/cm3，与围岩无明显的密度差。根据岩石密度资料统计，研究区花岗岩的平均密度为2.64g/cm3，古生界到中生界平均密度为2.69～2.73g/cm3，因此取花岗岩剩余密度为－0.05～－0.09g/cm3。

4.2 千里山岩体

千里山岩体位于茶陵－郴州逆冲地壳断裂带和大义山－郴州－大宝山断裂带交汇地带，该岩体矿集区是南岭花岗岩有色金属成矿最为典型的区域之一，其周围形成的柿竹园、红旗岭、东坡以及金船塘等著名的大型－超大型多金属矿床［32］（图7），历来是地质工作者研究的重点。在1∶20万重力异常图上，千里山岩体呈显著负异常特征，并与香花岭、骑田岭及诸广山岩体负异常相连，平行茶陵－郴州梯级带形成北东向负异常带，可能与深部隐伏的岩浆迁移通道有关。采集了千里山1∶2 000高精度重力剖面数据，除去浅表干扰，异常曲线如图8a所示。剖面南北向，布格重力异常以出露岩体为中心呈明显负异常特征，幅值达－26×10－5m/s2，异常形态南陡北缓。

对千里山岩体重力剖面进行蚁群算法反演时，将剖面剖分为40×20个矩形截面棱柱体单元，蚁群系统的数量为200，信息素挥发系数为0.7，根据该区物性统计结果取该区花岗岩剩余密度为－0.09 g/cm3，蚁群系统搜索30次后收敛。图8b是经过千里山岩体重力剖面的蚁群算法探测结果。首先，蚁群算法反演快速、收敛稳定，较好地拟合了重力观测数据（图8a）。蚁群算法圈定的花岗岩岩体边界清晰，分布集中，揭示千里山花岗岩岩体深部规模较大，下底面延深达到16km。这说明出露岩体仅为该岩基的顶角，尤其在出露岩体的北部、毗邻茶陵－郴州断裂带附近有一定的隐伏规模，推测为深部岩浆迁移通道，并形成千里山－骑田岭－香花岭构造岩浆带。

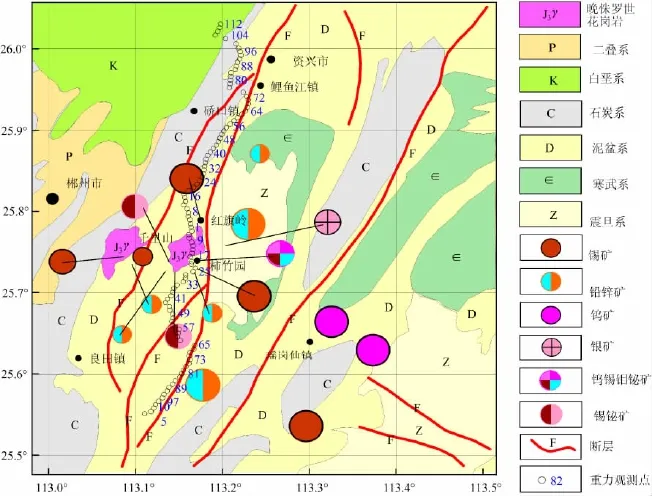
图7 千里山岩体区域地质图［32］及重力测点位置图Fig.7 Regional geological map of Qianlishan rocks and positions of gravity observation points

4.3 九嶷山岩体

九嶷山岩体位于我国著名的有色金属成矿区——湘南地区西南部、湘粤交界处，是南岭地区重要的锡成矿远景区之一。区内地质构造复杂，断裂构造发育，岩浆活动频繁，成矿地质条件优越［32］（图9）。在1∶20万重力异常图上，九嶷山岩体周围呈显著负异常，并且负异常在北部超出出露岩体。采集了九嶷山1∶2 000高精度重力剖面数据（图10a），剖面南北向，布格重力异常在出露岩体区域呈明显负异常特征，幅值达－24×10－5m/s2，且负异常在出露岩体北部有一定规模延伸。

对九嶷山岩体重力剖面进行蚁群算法反演时，将剖面剖分为40×20个矩形截面棱柱体单元，蚁群系统的数量为200，信息素挥发系数为0.7，根据该区物性统计结果取该区花岗岩剩余密度为－0.09 g/cm3，蚁群系统搜索31次后收敛。图10b是经过九嶷山岩体重力剖面的蚁群算法探测结果。首先，蚁群算法反演快速、收敛稳定，较好地拟合了重力观测数据（图10a）。蚁群算法圈定的岩体边界清晰，分布集中，且与区内出露岩体吻合。同时，大地电磁是揭示花岗岩体形态的重要手段，本次蚁群算法反演的结果与该剖面大地电磁测深反演结果（图11）相比，所得到的岩体侵入形态接近。蚁群算法和大地电磁测深揭示：该剖面上花岗岩侵入体为3个岩体的组合，从南往北，该剖面上花岗岩年代分别为侏罗纪、三叠纪及侏罗纪；最大延深达到22km，对应三叠纪岩体；而北部为隐伏岩体。反演结果揭示九嶷山复式岩体深部侵位形态较复杂。

图8 千里山岩体重力异常（Δg）蚁群算法反演结果Fig.8 ACO inversion results of Qianlishan rocks of gravity anomalies（Δg）

图9 九嶷山岩体区域地质图［32］及重力和MT测点位置图Fig.9 Regional geological map of Jiuyishan rocks and positions of gravity and MT observation points

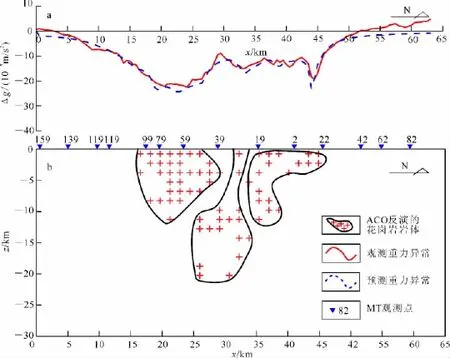
图10 九嶷山岩体重力异常蚁群算法反演结果Fig.10 ACO inversion results of Jiuyishan rocks of gravity anomalies

图11 九嶷山岩体2D大地电磁测深反演结果Fig.11 2DMT inversion results of Jiuyishan rocks

5 结论

蚁群智能算法在启发式随机搜索中展示出优异的性能，它是基于信息素的正反馈机制，具有较好的鲁棒性、并行性和可移植性。蚁群智能算法是继蒙特卡洛算法（Monte Carlo）、遗传算法（GA）、模拟退火（SA）和人工神经网络（ANN）之后的一种可以广泛应用于地球物理反演的完全非线性反演方法，在地球物理反演中有较好的应用前景。

改进的蚁群算法反演效果良好，其中九嶷山岩体的反演结果与大地电磁测深所揭示的岩体侵入形态吻合。蚁群系统探测千里山岩体延深达到16 km，北部具有一定隐伏规模，揭示了千里山－骑田岭－香花岭隐伏岩浆构造带的存在；九嶷山岩体延深达到22km，该剖面上分为3个岩体，北部为隐伏岩体。蚁群系统较好控制了千里山岩体和九嶷山岩体的延深、形态，为研究南岭地区花岗岩侵入模式和多金属成矿规律提供了参考。

（References）：

［1］秦葆瑚.湘南四个金属矿田的区域重磁异常特征［J］.物探与化探，1984，8（1）：34－40.Qin Baohu.Characteristics of Regional Gravity and Magnetic Anomalies of Four Major Polymetal Ore Fields in Southern Hunan，China［J］.Geophysical ＆Geochemical Exploration，1984，8（1）：34－40.

［2］秦葆瑚.湘南区域重磁异常的地质解释及其在成矿预测中的应用［J］.湖南地质，1984，3（2）：1－14.Qin Baohu.The Interpretations of Regional Gravity and Magnetic Anomalies and Their Applications of Minerogenetic Prognoses in Southern Hunan［J］.Hunan Geology，1984，3（2）：1－14.

［3］秦葆瑚.南岭区域重磁异常的地质解释［J］.湖南地质，1987，1（1）：1－15.Qin Baohu.A Geological Interpretation on the Regional Gravity and Magnetic Anomalies in Nanling Area［J］.Hunan Geology，1987，1（1）：1－15.

［4］李少莲.湘南地区隐伏地质构造与矿产预测［J］.矿产与地质，1990，4（3）：11－17.Li Shaolian.Concealed Geological Structure and Prediction for Mineral Resource in South Hunan［J］.Mineral Resources and Geology，1990，4（3）：11－17.

［5］段利华.湘桂粤赣区域性位场资料的数据处理及其应用［J］.矿产与地质，1991，5（4）：318－324.Duan Lihua.Regional Potential Field Data Processing and Their Application in the Area of Hunan，Guangxi，Guangdong and Jiangxi Province［J］.Mineral Resources and Geology，1991，5（4）：318－324.

［6］朱自强，黄国祥.柿竹园矿田重磁资料的三维反演及成矿预测［J］.矿产与地质，1996，10（1）：66－72.Zhu Ziqiang，Huang Guoxiang.3DInversion for Potential Field Data and Metallogenic Prognosis in Shizhuyuan Deposits［J］.Mineral Resources and Geology，1996，10（1）：66－72.

［7］饶家荣，金小燕，曾春芳.南岭中段北段深部构造：岩浆岩控矿规律及找矿方向［J］.国土资源导刊，2006，3（3）：31－36.Rao Jiarong，Jin Xiaoyan，Zeng Chunfang.Deep Structure of Middle and Northern Section：Magmatic Rocks Ore－Controlling Regularity and Prospecting Direction［J］.Land ＆Resources Herald，2006，3（3）：31－36.

［8］Dorigo M，Maniezzo V，Colorni A.The Ant System：An Autocatalytic Optimizing Process［R］.Milano：Politecnico di Milano，1991.

［9］Dorigo M，Maniezzo V，Colorni A.Ant System：Optimization by a Colony of Cooperating Agents［J］.IEEE Trans on Systems，Man，and Cybernetics：Part B：Cybernetics，1996，26（1）：29－41.

［10］Gambardella L M，Dorigo M.Solving Symmetric and Asymmetric TSPs by Ant Colonies［C］//Proceedings of the 3rd IEEE International Conference on Evolutionary Computation.Nagoya：IEEE Neural Network Council（NNC）and Society of Instrument and Control Engineers（SICE），1996：622－627.

［11］Dorigo M，Gambardella L M.Ant Colony System：A Cooperative Learning Approach to the Traveling Salesman Problem［J］.IEEE Transactions on Evolutionary Computation，1997，1（1）：53－66.

［12］Dorigo M，Gambardella L M.Ant Colonies for the Travelling Salesman Problem［J］.BioSystems，1997，43（2）：73－82.

［13］Gambardella L M，Dorigo M.Ant－Q：A Reinforcement Learning Approach to the Traveling Salesman Problem［C］//Proceedings of the 12th International Conference on Machine Learning.Tahoe：The International Machine Learning Society，1995：252－260.

［14］Stutzle T，Hoos H.Improvements on the Ant System：MAX－MIN Ant System［C］//Proceedings of the International Conference on Artificial Neural Networks and Genetic Algorithms.Wien：Springer Verlag，1997：245－249.

［15］Stutzle T，Hoos H.MAX－MIN Ant System and Local Search for the Traveling Salesman Problem［C］//Proceedings of the 4th International Conference on Evolutionary Computation.Indianapolis：IEEE Neural Network Council（NNC）and Evolutionary Programming Society（EPS），1997：308－313.

［16］Maniezzo V，Colorni A.The Ant System Applied to the Quadratic Assignment Problem［J］.IEEE Transactions on Knowledge and Data Engineering，1999，11（5）：769－778.

［17］Gambardella L M，Taillard E，Dorigo M.Ant Colonies for the QAP［R］.Lugano：Istituto Dalle Molle di Studi Sull’Intelligenza Artificiale（IDSIA），1997.

［18］Gambardella L M，Taillard E，Dorigo M.Ant Colonies for the Quadratic Assignment Problem［J］.Journal of the Operational Research Society，1999，50（2）：167－176.

［19］Stützle T，Hoos H.MAX－MIN Ant System and Local Search for Combinatorial Optimization Problems［C］//Stefan V，Ibrahim H O，Catherine R.Meta－Heuristics：Advances and Trends in Local Search Paradigms for Optimization.Norwell：Kluwer Academic Publishers，1997：137－154.

［20］Maniezzo V.Exact and Approximate Nondeterministic Tree－Search Procedures for the Quadratic Assignment Problem［J］.Informs Journal on Computing，1999，11（4）：358－369.

［21］Colorni A，Dorigo M，Maniezzo V，et al.Ant System for Job－Shop Scheduling［J］.Belgian Journal of Operations Research，Statistics and Computer Science，1994，34（1）：39－53.

［22］陈双全，王尚旭，季敏，等.地震波阻抗反演的蚁群算法实现［J］.石油物探，2005，44（6）：551－553.Chen Shuangquan，Wang Shangxu，Ji Min，et al，The Ant Colony Algorithm for the Seismic Impedance Inversion［J］.Geophysical Prospecting for Petroleum，2005，44（6）：551－553.

［23］严哲，顾汉明，赵小鹏.基于蚁群算法的非线性AVO反演［J］.石油地球物理勘探，2009，44（6）：700－702.Yan Zhe，Gu Hanming，Zhao Xiaopeng.Non－Linear AVO Inversion Based on Ant Colony Algorithm［J］.Oil Geophysical Prospecting，2009，44（6）：700－702.

［24］Yuan S Y，Wang S X，Tian N.Swarm Intelligence Optimization and Its Application in Geophysical Data Inversion［J］.Applied Geophysics，2009，6（2）：166－174.

［25］Li Y G，Oldenburg D W.3－D Inversion of Magnetic Data［J］.Geophysics，1996，61（2）：394－408.

［26］Li Y G，Oldenburg D W.3－D Inversion of Gravity Data［J］.Geophysics，1998，63（1）：109－119.

［27］Dréo J，Siarry P.A New Ant Colony Algorithm Using the Heterarchical Concept Aimed at Optimization of Multiminima Continuous Functions［C］//Dorigo M，Caro G D，Sampels M.Ant Algorithms.Berlin：Springer Berlin Heidelberg，2002：216－221.

［28］Dréo J，Siarry P.Continuous Interacting Ant Colony Algorithm Based on Dense Heterarchy［J］.Future Generation Computer Systems，2004，20（5）：841－856.

［29］Socha K，Dorigo M.Ant Colony Optimization for Continuous Domains［J］.European Journal of Operational Research，2008，185（3）：1155－1173.

［30］Dorigo M.Optimization，Learning and Natural Algorithms［D］.Milano：Politecnico di Milano，1992.

［31］Dorigo M，Stützle T.The Ant Colony Optimization Metaheuristic： Algorithms， Applications， and Advances［C］//Glover F， Kochenberger G A.Handbook of Metaheuristics.Norwell： Kluwer Academic Publishers，2003：250－285.

［32］於崇文，彭年.南岭地区区域成矿分带性：复杂成矿系统中的时－空同步化［M］.北京：地质出版社，2009.Yu Chongwen，Peng Nian.Regional Ore Zonality of the Nanling Region：Spatio－Temporal Synchronization in Complex Ore－Forming Systems［M］.Beijing：Geological Publishing House，2009.