一种基于单调多边形的三角剖分算法

徐 敏， 朱二喜, ， 何援军

（1. 江苏信息职业技术学院，江苏 无锡 214153；2. 上海交通大学计算机工程系，上海 200240）

三角剖分是计算机辅助几何设计、几何造型及计算机图形学中研究的重要内容之一，在有限元分析、几何重构、数字地形分析、计算机图形学及机器人等领域有重大应用。

Chazelle[1]证明了多边形的三角剖分可以在O(n)时间复杂度内完成，但算法实现非常困难。肖忠晖等[2]以切耳算法[3]为基础，实现简单多边形的三角化。马小虎[4]等人提出的一种基于凹凸顶点判定的简单多边形Delaunay三角剖分算法，思路清晰，程序实现简单，剖分质量高，且计算效率相对较高。李学军等人[5]提出的快速算法，先将多边形分割成多个单调多边形，然后对单调多边形进行三角化，不过该算法只是在单调多边形三角化时的时间复杂度为O(n)，而在多边形单调化时复杂度比O(n)要高。毕林等提出的快速三角化算法[6]，在不考虑前期处理的情况下时间复杂度近似O(n)的多边形三角化算法，适用于带内孔的任意简单多边形，实现较为简单，计算量较少。

对于含有内孔的多边形（多连通多边形），可以通过引入桥边将其外轮廓线与内孔连接起来转化为退化的多边形。这种加入桥边运算复杂，程序结构也复杂，同时需要处理挂边现象。如陈向平等人[7]提出的桥边算法，邓先礼等人[8]对陈向平等人的算法进行改进。徐春蕾等人[9]提出的 GTP算法，将数据形成内外环两个链表，不适应于内环中还有环的情况。

本文提出的算法适用于含有任意个内孔的多边形，先根据边界y向局部极值顶点作出水平分割线，将多边形划分成单连通y单调多边形，然后再对单调多边形进行三角剖分，最终完成对初始多边形的三角剖分。

1 几何理论

定义1[10]边界顶点排序 多边形每一边界（外边界及内孔）的顶点按下列原则排序：当人顺着多边形边界行走时，他的左手指向多边形的内部。

按照定义1，对于凸多边形，这个原则意味着：多边形的外边界为逆时针走向，内边界为顺时针走向。而多边形的每一条边界均为一个向量，这个要求并不苛刻。

定义2[10]两向量交点的特征值 两向量交点的特征值由其矢量积的方向定义，特征值的绝对值取为 1。因此，两个向量交点的特征值有 2个，分别对应于求交的两个向量，且这2个特征值的符号相反，其代数和为0。如图1所示，两向量各种交点特征值的情况（其中的“＋”“－”符号是相对于中间水平直线的）。特别考虑了两向量间各种特殊位置的情况，这些特殊位置造成了几何奇异。

根据定义1和定义2，如果有任一向量与多边形的边界向量相交，则相对于该向量，若交点的特征值为-1，就意味从此交点开始，该向量进入多边形内部，称为“入点”，反之，该向量从此点离开多边形，称为“出点”。

图1 两向量交点特征值的各种情况

定义3单调多边形 一个简单多边形关于某条直线L单调，如果对任何一条垂直于L的直线L'，L'与多边形交都是连通的，即它们的交可能是一条线段，或者是一个点，或者是空集。

例如，一个多边形基于y坐标轴单调则称它是y单调多边形，它的一个鲜明几何意义是：从最高顶点沿着多边形的（左/右）边界走向最低顶点的过程中，始终是向下（或水平）的，即y坐标值最大和最小两个顶点可以将它的边分成两个单调边序列，如图2所示。

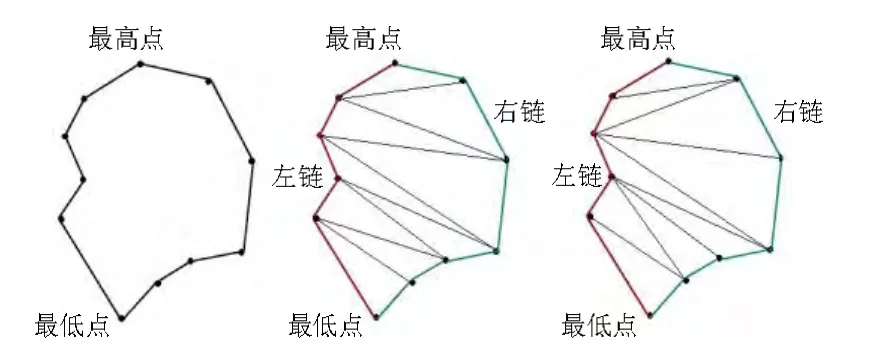
图2 y单调多边形及其三角化

一个单调多边形的“最高点”与“最低点”将单调多边形分成2个链，可以从上至下根据高度相邻原则连接两链间的顶点实现可三角化。图2给出y单调多边形的三角化的例子。

一般多边形不是y单调的原因是因为存在一些局部y极值点，如果排除这些y极值点，多边形就成为y单调的了。既然，最终的目的是将多边形三角化，因此，如果能在y极值点处将多边形分割，使形成y极值点的2条边分属于两个多边形，那么，在新的两个多边形中，该y极值点处y坐标就是单调的了。

2 算法描述

2.1 算法基本原理

本文算法先将一般多边形分割为y单调多边形，再将y单调多边形划分成三角形。所处理的图形可以有任意个外边界，每个外边界可以含有0到多个内孔。

一个y极值点（Ymax和Ymin点）与左右相邻边界顶点不是单调的，因此，一个简单的思想是在y极值点处分割图形就能达到极值点两边的边界成为y向单调。本算法的基本原理就是依据这个原理。先通过一个简单的例子阐述算法的基本思想。

如图3所示，图形含有1个外边界和2个内孔。找出所有边界中的局部y极值点（Ymax和Ymin点），此图中外边界为凸多边形，只需考虑内边界的y极值点，有2+2个。通过这些y极值点作水平线，一个极值点形成一条水平分割线。一般情况下水平分割线与图形的边界有很多交点，用于划分图形成y单调多边形的分割线的端点由这些交点中离极值点最近的左右2个交点构成，这样分割线就能有效地将图形划分的区域即为y单调多边形，如图3中4条分割线将原多边形分成7个y单调多边形。

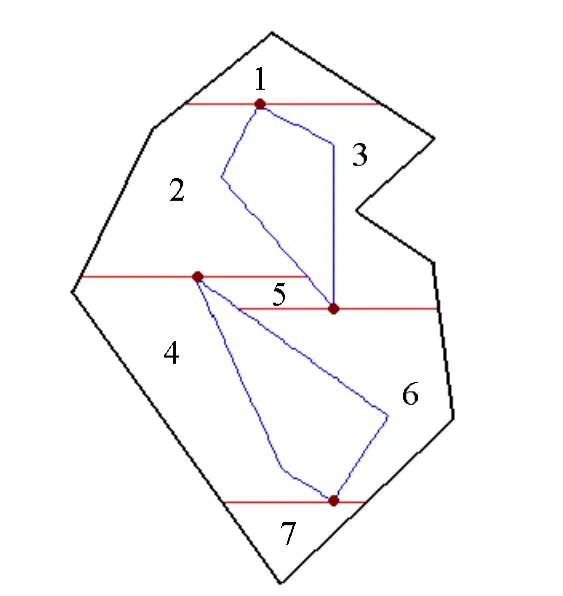
图3 多边形的y单调划分

2.2 y极值点分割线的算法

衡量一个算法的稳定性就是看它处理奇异情况的能力，本算法充分利用边界的方向性及交点特征值可以方便快捷解决这个问题。基本原则是：如果水平分割线与图形边界的交点是一个重交点，则利用定义2，把交点特征值代数和的符号作为重交点特征值的符号，当2个重交点的特征值代数和不为零时，保留其中一个交点，特征值绝对值仍取为 1，符号不变；2个重交点的特征值代数和为零时，取消重交点，如图 4、图 5所示。

y极值点分割线的算法课简述如下：

1） 对图形中每一局部极值点作自左至右的水平向量（该向量的左端点和右端点均需超越整个图形以保证与所有边界均能求交）；

2） 求取该分割线向量与图形各边界的边向量的交点及交点相对于该分割线向量的特征值（图4中标有“○-”、“○+”的交点）；

3） 对所有交点（及其附带的特征值）自左至右（即按水平方向的x值从小到大）排序；

4） 处理重交点，如果水平分割线通过图形边界的顶点（此时2个交点的x值相同，图4中7、8），就形成重交点。当重交点特征值代数和不为零时，保留其中一个交点，特征值绝对值仍取为1，符号不变；重交点的特征值代数和为零时，取消重交点；

5） 处理重边交点，如果水平分割线与图形某边界重合（此时2个交点的x值不相同）就形成重边交点。此时如果重交点的2个特征值均为“+”，取消后一个重交点（图4中1、2取1），如果 2个特征值均为“-”，取消前一个重交点（图4中3、4取4）；

6） 如果有交点，则取y极值点左面最近的“-”特征交点与右面最近的“+”特征交点作为该y极值点分割线的端点。否则，该y极值点分割线不计（图4中①、②）。

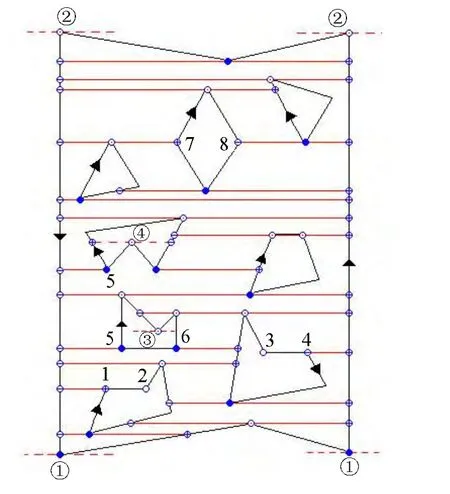
图4 带有几何奇异的图形

2.3 y单调多边形划分算法

一般多边形转化成y单调多边形的基本原理很简单，实施却很复杂，因为算法将处理含有内孔的多边形，且包含复杂的奇异状况。下面的算法将任意的多边形区域划分成若干个y单调多边形。算法可分成两部分：（1）求取分割线；（2）对y单调多边形（参阅图4）。

2.3.1 边界顶点排序

对多边形的每一边界顶点按照定义2排序，边界前进方向的左侧为内部。

2.3.2 求局部极值点

求取所有边界顶点铅垂方向的局部极值点（Ymax和Ymin点）（图4中局部最低顶点以“●”表示，局部最高顶点以“⊙”表示）。

2.3.3 作水平分割线

对每一局部极值点，执行“y极值点分割线的算法”。

2.3.4 建立“标记点”

建立下列点作为“标记点”：

1） “节点点”：将所有负交点（“○-”点）及局部最低顶点（“●”）作“节点点”标记。从每个节点点出发就可搜索到一个 y单调多边形，即“节点点”数就是划分的总y单调多边形个数。其中，如果负交点不在任何边界的顶点上，则需将其插入到所在边界的顶点队列中。

2）“上变向点”：将所有正交点（“○+”点）作“上变向点”标记。如果正交点不在任何边界的顶点上，则需将其插入到所在边界的顶点队列。

3） “下变向点”：对所有在分割线上的局部极大点（“⊙”）作标记，记为“下变向点”。即每条分割线段的左端点为“节点点”，右端点为“上变向点”，位于分割线段上的局部极大点为“下变向点”。

2.3.5 标记点连接关系

对每一非退化成一个点的分割线段执行下列操作：

1） 对每一分割线段，从左至右，对“节点点”和“上变向点”排序，建立后序关系。

2） 对每一分割线段，从右至左，对“上变向点”、“下变向点”和“节点点”排序，建立前序关系。

2.3.6 执行“单调多边形构建算法”

按照下面流程完成单调多边形。

N1【开始一个新节点】：依次取一“节点点”，Flag←1，记录该点为“首点”，并开始一个新节点。

N2【取下一点】：如果Flag＝1，取下一个“标记点”，否则取下一个“边界顶点”。

N3【回到首点？】：如果是“首点”，则已找到一个封闭单调多边形。对该单调多边形做三角化。记录三角化数据，“首点”作已用标记，转N5。

N4【到标记点？】：如果是“标记点”，Flag←1-Flag，转 N2。

N5【结束？】：如果“节点点”完，则算法结束，否则转N1。

这样整个多边形被分割线分为多个y单调多边形。

图5是水平分割线划分图4的结果。

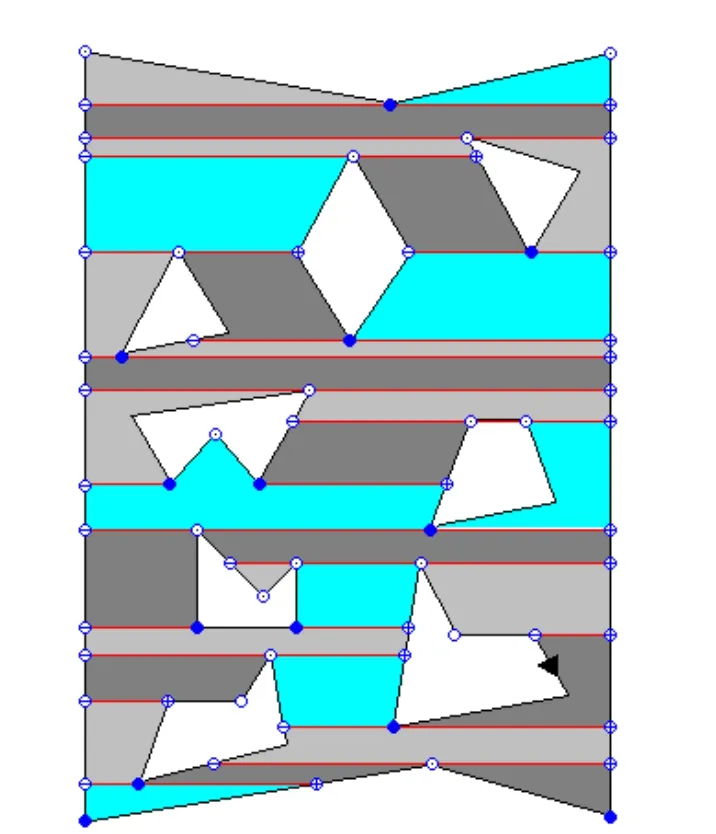
图5 通过水平分割线分割以后形成的节点区域

3 数据结构

算法的数据结构包括：多边形的数据结构、划分节点水平分割线的数据结构、y单调多边形的数据结构。这里沿用何援军教授在文献[10]中定义的3种数据结构。

4 算法实例

通过VC6.0开发工具实现该算法，并运行在XP系统上，对多个任意形状的多边形进行测试，如图6所示，选取具有代表性的4个例子，分别列出水平分割线将原图形分割之后的结构，以及分割之后对分割出来的y单调多边形进行三角化的结果。

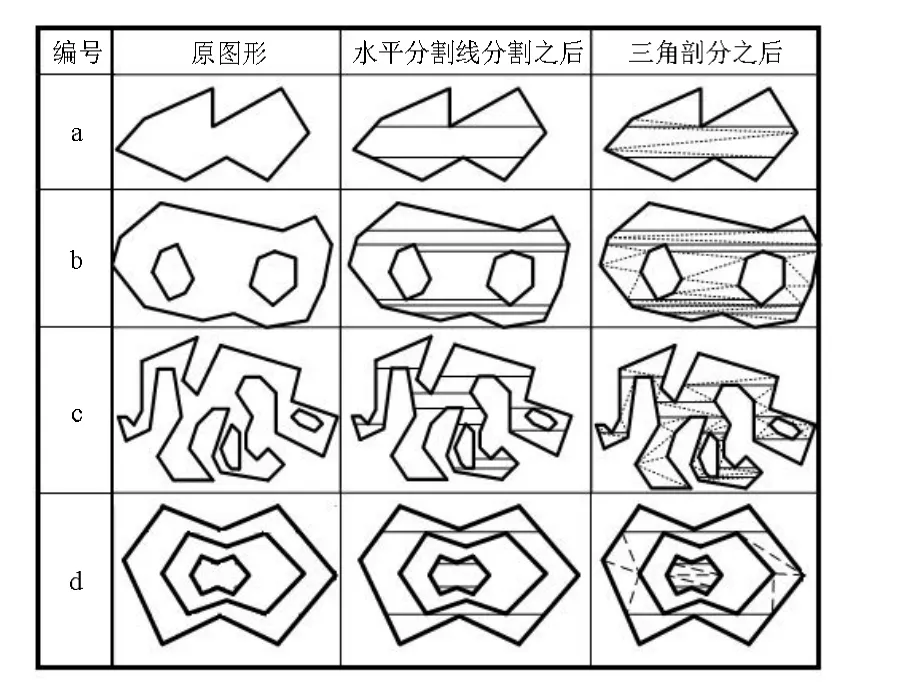
图 6 三角化例子

由图6的案例可以看出，该算法采用分割线很好的将任意的多边形划分为多个单调多边形，从而快速实现三角化，同时对含有岛的多边形也有较好的处理。算法实现的过程稍微复杂，是因为考虑到在用分割线分割图形时，水平向量与多边形相交时的一些奇异情况，但运用交点的特征值，很好的处理了这些奇异情况，并取得较好的效果，因此，具有更广泛的应用价值。另外对原有图形中重点重边问题也有一定解决。如图7所示，图7(b)中的A点是内孔与外边界的重点，也可以是原图形的自交点，并且又是局部极值点，对A点处理应该有一条水平分割线。图7(a)中A点同图7(b)一样，但该点的性质如图4中的②情况一样，对此点应没有分割线；但AB又是内孔与外边界的重边，在进行水平分割线分割之后，形成3个单调多边形和AB线段。图7(c)中的A、B两点与图7(a)图的A点一样，处理时应没有分割线。

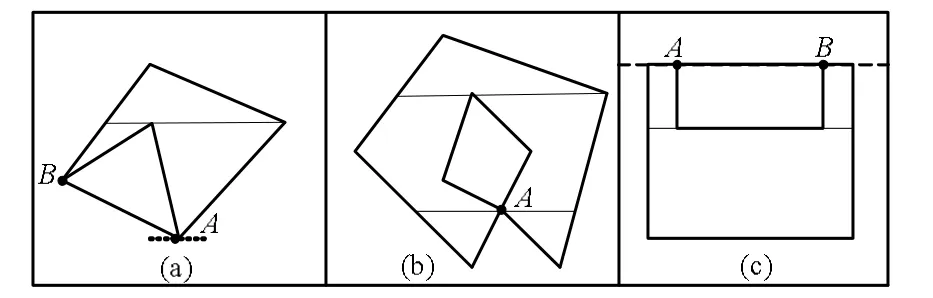
图 7 对奇异情况的处理

5 总 结

本文提出的算法可用于带0个或多个的内环任意平面多边形区域的三角化，也可以扩展到含有岛的任意多边形三角化，因此,是一个通用的三角化算法。本算法先对边界走向进行定义，通过边界y轴（或x轴）方向的局部极值点的分割线将多边形从上向下（或是从左到右）进行分割，采用交点的特征值比较彻底地解决了分割时的重点问题，将多边形区域准确地划分成若干个y单调多边形（或x单调多边形）。本算法原理简单易实施，适合于任意复杂的多边形，因而具有很好的鲁棒性。

[1]Chazelle B. Triangulating a simple polygon in linear time [J]. Discrete Comp Geom, 1991, 6(5): 485-524.

[2]肖忠晖, 卢振荣, 张 谦. 简单多边形凸单元剖分的编码算法[J]. 计算机辅助设计与图形学学报,1996, 8(增刊): 120-127.

[3 ]Kong X S, Everett H, Toussaint G T. The grahams can triangulates simple polygons [J]. Pattern Recognition Letters, 1990, 11(11): 713-716.

[4]马小虎, 潘志庚, 石教英. 基于凹凸顶点判定的简单多边形Delaunay三角剖分[J]. 计算机辅助设计与图形学学报, 1996, 7(4): 1-3.

[5]李学军, 黄文清. 平面区域三角化的快速算法[J].计算机辅助设计与图形学学报, 2003, 15(2):233-238.

[6]毕 林, 王李管, 陈建宏, 冯兴隆. 快速多边形区域三角化算法与实现[J]. 计算机应用研究, 2008, (10):3030-3033.

[7]陈向平, 应道宁. 统一于NIP的多边形三角剖分算法[J]. 计算机学报, 1989, 12(3): 194-199.

[8]邓先礼, 胡 达, 杜小平. 多连通多边形三角化找桥算法的研究及实现[J]. 计算机与现代化, 2004, (5): 4.

[9]徐春蕾, 李思昆. 一种适用任意平面多边形的三角剖分算法[J]. 国防科技大学学报, 2000, 22(2):82-85.

[10]何援军, 孙承山, 曹金勇. 绣花缝针轨迹问题[J].计算机学报, 2003, 26(9): 1211-1216.