图学计算基础

于海燕， 蔡鸿明， 何援军

（1. 东华大学机械工程学院，上海 201620；2. 上海交通大学计算机系，上海 200240）

当今计算机体系无法有效解决未来应用对功能性提出的越来越高的要求，“人脑计算机时代”将挑战统治计算机结构50余年的冯·诺依曼体系[1]。同样，图学计算，作为图学学科的基础，对其计算精度要求越来越高，原有体系的稳定性日益受到挑战，一些原以为已成熟的算法逐渐暴露出问题。因此，有必要对图学计算的内涵、关键问题、研究方法进行梳理与研究，探索稳定、快速的图形计算新理论与方法。

本文首先揭示图形、图像和视频的本质，探索图学计算的内涵，构造图学的公共基础。从表现的视角理解图形/图像只是基本图元不同组合的显示方式，揭示图形/图像的几何特性；从对图形/图像产生机理的梳理入手，分析图形计算的矛盾，明确图学计算的根本任务；从几何奇异是造成几何计算不稳定性的本源入手，把握图形计算的关键。

结合最新研究进展，总结提炼图学计算的研究动向，并基于计算与几何两个最核心的要素，进一步阐述一种有别于代数化的几何化计算理论。

1 图学计算内涵

回顾计算历史，从石块、贝壳到结绳计数，到算盘的出现，再到计算机的诞生，随着科学技术的发展，人类社会进入了一个崭新的计算时代。从计数到推理、由实践到理论，从自然科学到哲学命题，人类对于计算的认识在不断深入。

人类的思维是基于图形的。人类的计算历史与人从孩童到成年对数学的认知历程一样，也始于图形，由具体的形，到抽象的形，再到更抽象的图。至今我们仍习惯于通过在纸上涂涂画画的方式把复杂的问题分解提炼，抽象出其本质，说明人类的计算是源于图形、基于图形的。

尽管图形与图像的处理方式存在差异，但是他们的计算基础是相同的——从表现的视角理解，图形与图像都只是具有线形、宽度、颜色等属性信息的基本图元（点、线等几何）的不同组合。例如，计算机图形学中的隐藏线消除算法与真实感图形绘制算法是分别由三维场景生成图形和图像的典型算法。两者在三维空间的主要计算都是直线（向量）与空间物体的求交计算，计算的目标都是为了求得空间点，前者是2个点，后者是1个点，只是在最后的显示阶段，他们的工作才各走自己的路，一个取2个点得到线段及线的宽度、线型、颜色等属性，组成图形；另一个则只需计算1个点的色调、色饱和度和亮度等属性，得到像素，组成图像。

因此，组成图形与图像的基元是几何，图学计算的本质是几何计算。

1.1 图、形、几何与几何计算

世界由形构造，形由图在画面上显示，形是图之源。计算机背景下，图学的主要工作是由图显示形，由图构造形，以及由一张图变成另一张图。

在计算机中，形与图均由几何描述，这里的几何是点、线、面，常被称为“几何元”，这些不同的几何元依照一定的拓扑关系构造成不同的场景，在空间构造形；通过投影在平面显示图，此时，点、线常被称为“图元”，不同属性图元的组合构造了所有的图形或图像。

用两个典型的例子说明图、形、几何与几何计算的关系。隐藏线消除是由形显示为图形的典型算法。消隐过程是一条一条线的输出，每条线需与场景中所有物体（面）进行比较，线的各可见部分的交集即为此线的最终可见部分。因此，整个场景的输出（显示）过程就是一条一条地去确定场景中所有线条的哪些部分该显示，哪些部分不该显示。这涉及大量的几何运算和代数运算。真实感图形绘制是由形显示为图像的典型算法。这是一个光强与色彩的量化、纹理映射、图像合成、帧缓存等基于物理、光学、色彩理论和技术的复杂计算过程。这里，贯穿整个算法的关键计算是从光源发出的每一条光线与景物表面的空间线面的求交，包括反射和折射计算，都是几何求交、比较等的几何计算。

基于以上分析，本质上，图、形、几何与几何计算的关系可以简单的表述为：形是表示，是输入，图是展现、是输出；形与图的基本元素是几何，形的构造与图的形成的本质是几何的定义、构造、度量和显示。

1.2 图形的本质

人工生命理论的创立者兰顿(Chris Langton)认为[2]，生命的本质不在于具体的物质，而在物质的组织形式；这种组织原完全可以用算法或程序表达出来，所以，只要能将物质按着正确的形式构建起来，这个新的系统就可以表现出生命。”而这种所谓的“正确的形式”就是生命的算法或程序。所以，算法和程序是把非生命和生命连接起来的桥梁，是生命的灵魂。这在图上也体现出来，下面以两个简单例子说明这个论点。

图1(a)表示平面上由4个点构造的矩形，它们的拓扑关系为1-2-3-4-1。图1(b)是保持拓扑关系而改变其中一个点(3)的几何参数，它仍能揭示原图的基本构图形状。而图1(c)则仅改变了4个点之间的连接关系，几何参数完全相同的点因拓扑关系的不同而构成了完全不同的图形。

对图 2左上角所显示的三维空间框架施以不同的裁剪，就得到不同的图，这些图反映在人们大脑中是不同的形，或是实心的、或是空心的、或是盒子，等等。这里，空间线的几何参数并没有改变，只是线的部分被用于构成图形，本质上也是几何元的拓扑关系改变导致展现了不同的形。

图1 图元关系的改变导致图的大变形

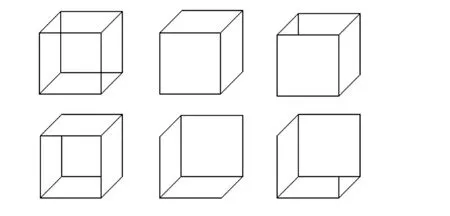
图2 几何元的不同部分展现了不同的形

因此，图形的本质不是构成图形的图元本身，而在于图元的组织形式，决定于图元之间的相互关系。

1.3 图形计算的矛盾

还有一个问题存在于图形计算的过程中：“形是二维或三维的，图是二维的，计算是一维的。”其实，长期以来人们习惯的基于代数的数计算一直蕴涵着“一维计算处理二维问题”这样一个矛盾，遗憾的是，这个矛盾并没有引起人们足够的重视。正如吴文俊先生总结数学机械化的实质是“把质的困难转化为量的复杂”一样，人们习惯于这样的复杂。

计算不应该仅仅局限于数的一维计算机制，也要考虑形的二维形计算机制。有必要厘清形、数、人在图形计算中的特点与关系，尽可能充分的发挥各自的作用，探索形、数、人相结合的图形计算理论，探索求解图形问题的新方向、新方法。应该以人的三维思维，从形的角度，依赖于几何计算、数字计算以及计算机的算法等去构建图学的计算基础。

1.4 图形计算的关键

一种计算方法的提出，一个算法的设计首先要考虑的因素就是较高的稳定性，较低的复杂性，再考虑易读性、可交流性等伴随要求。计算的复杂度与稳定性是计算的两个关键问题，也是图学计算中的关键问题。

计算复杂度包括空间复杂性和时间复杂性。空间复杂性一般指存储量的问题，时间复杂性则是指计算的工作量问题。一般从量与质两个方面去降低计算的复杂度，或者减少计算对象的数目，或者降低参与计算对象的复杂度。

计算稳定性问题是一个长期的难题，本质是计算正（准）确性问题。即使在一些已被广泛使用的大型应用系统中，也存在几何引擎的稳定性问题。这里有理论问题，也有实施问题。导致几何计算不稳定主要有两个原因，一是由数字计算误差引起，通常与数制及计算方法有关；二是由几何本身原因引起，因几何间的重叠（共点、共线、共面等）引起的几何奇异而造成判断的不确定性。

2 研究动态

图形计算基于传统的数学理论、几何与代数。由于计算机的介入，代数计算发挥了更多的作用，但是，对图形来说，它的基本元素是点与线，因此在图学中应更多的发挥几何本身的特性。国外在这方面做了很多的工作。

文献[3]提出了一个隐式曲面（例如仿射度量、共线法线向量和法线向量、仿射高斯、平均曲率）的局部仿射结构的估计量，给出了一个更加简单和稳定的几何简化，避免了直接求导而导致的巨大的计算量和数据的不稳定。文献[4]通过空间有理立方 Bezier曲线研究了拉格朗日几何插值。此论文展示了在某些自然条件下，插值问题的解是存在并唯一的。论文中多个例子说明了非线性几何细分算法的应用前景。文献[5]通过单调螺旋五次曲线研究了包含终点、切线、曲率的几何Hermite数据插值。基于对空间Pythagorean速度曲线的Hopf映射方程，论文展现了通过解决某一单一变量 12维的多项式方程可以决定几何Hermite插值。文献[6]通过开发一套系统的运动轨迹描述机制来实现有效的运动轨迹描述。论文作者提出了一个灵活的运动轨迹信号描述工具，采用移动框架技术实现公式化运动轨迹再生。该研究在机器人学习等方面将有较广阔应用前景。

文献[7]采用光线投射法(ray casting)表示圆球，避免了采用多边形化(polygonization)方法表示带来的缺陷，并提出了一种基于 GPU的快速光线投射方法来渲染圆球，很好地解决了因此带来的大量计算。文献[8]提出了一个渲染大型复杂场景下图像的全局光照效果的软件系统，通过采用GPU，大幅提高了整体的渲染速度。

文献[9]提出了基于二维空间的光线传播模型，建立了用来简化复杂的全局光照理论的理论框架。这种概念上“降维”的方式带来了不少切实的好处：各种全局光照概念在2D中的可视化变得更加容易；处理2D光线传输及其派生物所需的计算时间大幅减少，这使建模和实验更加简单；由于2D中光线传输的表达式比较简单，复杂的全局光照概念的导出变得相对容易；文中描述的2D全局光照框架也有在教育方面的潜在应用。文献[10]提出了一种从3D图像中识别并提取出重复出现的结构的计算架构，通过一种对相似变换(similarity transformations)的恰当表示将该问题规约到2D的网格中，采用了一种优化算法来探测这些网格。该算法在有异常值和缺失信息的情况下也有很好的稳健性，因此在复杂且紊乱的图中也可以有效地发现重复结构。文献[11]介绍了一种分层发型合成架构，它把发型同时看作一个3D向量场和一个发束在头皮上的2D分布图，只需提供一种真实的发型，就可以合成一个从空间的发束到几何细节都满足统计上相似的模型。

从以上文献可以看出，近年，在代数化的基础上，几何问题已经倾向于采用更简洁直观的几何方法。这种方法的推进，还需要理论层面的支撑。

3 几何化的图学计算理论与方法

围绕图学计算的矛盾与关键问题的研究，我们已经建立了“几何问题几何化”的几何计算的全新理论框架及整套实用算法，处理几何表示、几何创建和几何计算中的各种问题。根据几何问题几何化的理论，国内学者提出了以“形计算”补充“数计算”的论点，构建了基于“几何基”和“几何数”的“形计算”机制，对数计算的非可读性、几何奇异引起的计算不稳定性等方面有了较大的改善。

1） 以形学统一几何与画法几何理论

现在似乎没有人将画法几何列入几何的范畴。其实，画法几何研究的基本对象也是几何，也是研究形的科学。国内学者已经从形的角度去揭示画法几何与几何的共性问题，将其应用于几何计算中[12-14]。探索以形为核心，综合地、巧妙地融合几何、画法几何、代数与计算机的多学科理论与方法，将各学科的长处融合在一起。反过来，这又为画法几何计算化提供了一条新途径，这是多学科理论与方法的融合与相辅相成。

2） 以图统一图形与图像

传统意义上的图形与图像是有区别的。计算机科学与技术的发展使图形与图像的区别逐渐被模糊化，例如在计算机屏幕上，展现在人们面前的，不管是图形还是图像，都是由离散的像素组成的画面（图）。因此，在计算机语境下用“图”来统称图形与图像是合适的，这种统一对图学科学的发展是十分有益的，它统一了图学计算的源头。

3） 数计算与形计算构成完整的算学

上世纪 80年代起，国内外就利用现代计算工具对画法几何等传统形计算进行改造，但大都采取代数化思路，掩盖了其本身的光芒。其实，形一般是二维以上的，它的关键是几何间的拓扑关系，代数是一维的，它是线性的有序的运算，两者的矛盾十分明显。在Leibniz“形式化整个数学，使之变成一个庞大的代数机器”的学术目标影响下，图形本身的直观、简洁优势似乎荡然无存，更减弱了人类直觉这个最有力的武器。图学计算的关键字是图，计算也应基于图，因此，用包含形计算与数计算的算学来统一图学的计算基础更为合理。

4） 几何计算理论

文献[12]首次以“几何计算”的方式阐述几何算法，认为几何的定义、构造、度量、显示以及相关处理（几何相交、几何碰撞、几何分析等）就是几何计算。与数字计算是以“数字”作为计算对象不同，几何计算以各种“几何”作为计算对象，研究基于几何（元）计算的理论与方法。通过引入几何基与几何数，构建了一个几“几何问题几何化的几何计算的理论体系和实施框架。将求解几何问题变成为如何寻找这些几何基的某一个序列，使计算的每一个步骤带有几何意义，形成一种形计算机制。 主要包括以下理论：

· 几何问题几何化：几何代数化并非是解决几何问题的必由之路，顺其自然是处理问题的最好方式，回归几何，淡化几何问题的代数（方程）方法，强调从几何的角度，用几何的方法去处理几何问题。

· 解表述的多样化：在计算机科学高度发达的今天，有必要重新审视计算结果的表述形式，不能一味追求所谓显式解，应该考虑几何、代数、画法几何、计算机科学等综合的理论、计算方法、方式与计算结果表述。

· 形计算机制：提出了一种基于几何的形计算机制，它是对传统数计算的一种补充。这个形计算机制基于以下两点认识基础。引入“几何基”，用几何基的序列构造几何解。在数计算层面，充分利用笛卡儿创立的坐标几何思想，用几何代数化方法构建一些基本几何基，作为常用的作图工具。在形计算层面，则是从几何的角度，去寻求几何问题的几何基求解序列。

· 几何计算的稳定性：计算的复杂度与稳定性是计算的两个关键问题。一种计算方法的提出，一个算法的设计首先要考虑的因素就是较高的稳定性，较低的复杂性，再考虑其他易读性、可交流性等伴随要求。引入“几何数”，用几何数更好的表示问题的几何结构和几何性质，使几何奇异的判定与解决转化成几何数的简单数字运算，从理论上构建了一个解决几何奇异问题的完整解决方案。简化几何计算的复杂性，使几何计算的稳定性和计算效率大大提高。

文献[15]对这种几何化的图学计算理论的应用作了探索，提出了一种基于投影降维的空间两三角形求交检测算法。引入“计算坐标系”，如图3所示，使“几何奇异”状态最后归结为平面上线段被三角形裁剪时的共点、共线问题，如图4所示，简单而明晰，从理论上保证了算法的鲁棒性。

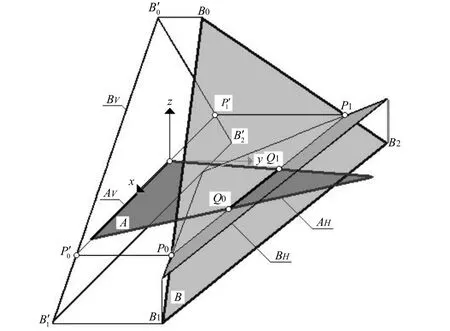
图3 计算坐标系下两三角形交线的计算

图 4 水平线段与三角形位置分布的奇异情况

4 总 结

图学计算的基础面临新的挑战，为此需要更优秀的图学计算理论、算法和系统架构，从而满足精确性、鲁棒性和可扩展性的需要。图学计算将向着多元化、多学科相融合的方向发展，稳定性将成为图学计算的研究热点与难点。

本文从图形计算的内涵与本质分析出发，指出几何代数化方法存在的用一维的代数方法决定二维几何关系的矛盾；结合图形计算的最新动态与应用需求，指出图学计算基础革新的趋势：探索一种发挥几何直观简洁特点的几何化求解方法，追求形、数结合的新突破。

几何问题几何化理论是具有革新意义的基础理论，它与形计算机制将挑战数百年来的几何代数之路。具体而言：淡化几何问题的代数化方法，“回归几何”，扩大几何的自然属性在几何问题求解中的作用，解决“用一维的代数方法去决定二维几何关系”的矛盾；探索一种“从定性、直观的角度去思考，以定量、有序的方式去求解”的图学计算理论和方法，达到形思考、数计算或定性思考、定量求解的境界；寻求建立一种“三维思维，二维图解，一维计算”的多维空间融合，追求形、数结合突破的形计算机制。此外，今后的研究会更关注于计算稳定性问题。完善基于“几何基”和“几何数”的“形计算”机制，将对数计算的非可读性、几何奇异引起的计算不稳定性等方面有较大的改善。

[1]何 屹, 毛 黎. 开启计算机“高智商”新时代[N].科技日报, 2011-08-20 (002).

[2]Piccinini G. Computationalism in the philosophy of mind [J]. Philosophy Compass, 2009, 4(3): 515-532.

[3]Andrade M, Lewiner T. Affine-invariant curvature estimators for implicit surfaces [J]. Computer Aided Geometric Design, 2012, 29(2): 162-173.

[4]Jaklic G, Kozak J, Krajnc M, Vitrih V, Zagar E.Geometric lagrange interpolation by planar cubic Pythagorean-hodograph curves [J]. Computer Aided Geometric Design, 2008, 25(9): 720-728.

[5]Han C Y. Geometric Hermite interpolation by monotone helical quintics [J]. Computer Aided Geometric Design, 2010, 27(9): 713-719.

[6]Wu S, Li Y. Motion trajectory reproduction from generalized signature description [J]. Pattern Recognition, 2010, 43(1): 204-221.

[7]Kanamori Y, Szego Z, Nishita T. GPU-based fast ray casting for a large number of metaballs [C]//EUROGRAPHICS, 2008, 27.

[8]Budge B, Bernardin T, Stuart J A, Sengupta S, Joy K I,Owens J D. Out-of-core data management for path tracing on hybrid resources [C]//Eurographics, 2009, 28.

[9]Jarosz W, Schönefeld V, Kobbelt L, Jensen H W.Theory, analysis and applications of 2D global illumination [C]//SIGGRAPH, 2012.

[10]Pauly M, Mitra N J, Wallner J, Pottmann H, Guibas L.Discovering structural regularity in 3D geometry [C]//SIGGRAPH, 2008.

[11]Wang L, Yu Yizhou, Zhou Kun, Guo Baining.Example-based hair geometry synthesis [C]//SIGGRAPH, 2009.

[12]何援军. 几何计算[M]. 北京: 高等教育出版社,2013.

[13]何援军. 对几何计算的一些思考[J]. 上海交通大学学报, 2012, 46(2): 18-22.

[14]何援军. 几何计算及其理论研究[J]. 上海交通大学学报, 2010, 44(3): 407-412.

[15]于海燕, 何援军. 空间两三角形的相交问题[J]. 图学学报, 2013, 34(4): 54-62.