紧致优化DGHV全同态加密方案*

2013-09-25汤殿华曹云飞杨浩淼

通信技术 2013年12期

汤殿华，曹云飞，杨浩淼

0 引言

全同态加密是一种功能强大的加密技术，能够在加密数据上执行任意的计算，同时将对应的计算映射到明文中，其计算结果仍为密文。可以说，全同态加密技术能够全密态处理数据。采用该加密技术，可以将数据以加密形式外包给任何不可信服务器进行“密文计算”来获取服务，保证了数据安全。全同态加密技术具有广阔的应用前景，例如云安全、加密数据库、密文检索、网络编码［1］、搜索引擎的加密询问等。

同态密码技术对我们并不陌生，例如 RSA［2］、ElGamal［3］、Paillier［4］等加密方案。这些加密算法都具有同态性，但只有单个同态运算性质，不能同时具有“加同态”和“乘同态”，以致不能够执行任意的密文计算。1978 年，Rivest，Adleman，Dertouzos［5］首次提出了这种“隐私同态”的概念，希望解决密文任意计算问题。直至2009年，Gentry基于理想格提出了第一个全同态加密方案［6］，实现了“隐私同态”的构想。

Gentry的方案基于理想格数学结构，运算复杂。Dijk等人避免了这种复杂的代数结构，提出一个整数上的全同态加密方案—DGHV方案［7］，其运算完全基于整数运算，更容易理解。全同态加密方案除了满足能够无限计算“同态加”和“同态乘”之外，还应满足紧致性:密文尺寸需要保持有界，不能随着同态操作而无限增大。在DGHV方案中，其类同态方案(Somewhat Homomorphic Scheme)的同态乘和同态加操作没有进行类似于加密算法中的模运算，导致了密文尺寸的不断增加。为了保证全同态加密方案的紧致性，DGHV方案的同态解密算法，在更新密文噪声的同时，也将密文尺寸控制在˜O(λ7)的水平，但在同态解密算法的内部运算过程中，密文数据的尺寸仍在不断增加。

文中给出了一个紧致优化技术，使得DGHV方案中类同态方案和全同态方案均满足紧致性要求，密文尺寸始终保持在˜O(λ5)以内，而且保证了同态解密算法的内部运算的密文尺寸不增加。

1 准备知识

定义1 同态加密方案。同态加密方案由四个概率多项式时间算法组成 HE=(KeyGen，Enc，Dec，Evaluate):

KeyGen:根据安全参数λ，生成方案的公钥pk、私钥sk。

Enc:给出一个明文m，用公钥pk加密明文m，得到密文c。

Dec:输入私钥和密文c，进行解密运算，输出明文m'。

Evaluate:输入公钥 pk，t输入线电路 Cir，一组密文 →c=(c1，c2，…，ct)，其中 ci=Encpk(mi)。输出 c*=Evaluate(pk，Cir，→c)，且满足 Dec(sk，c*)=Cir(m1，m2，…，mt)。

由定义1可以看出，同态加密方案除了包括传统公钥加密方案的所有算法(KeyGen，Enc，Dec)之外，还包括一个额外的运算算法Evaluate。该算法是用于同态处理一个电路，是方案同态性的体现，能够在不解密条件下，对密文的操作实现了相应的明文操作，并且操作结果也为密态。

文中研究的方案是单比特的加密形式，即明文空间为{0，1}，所运算的电路为布尔电路，这样就可以对应于计算机中的数字逻辑电路，而计算机所完成的所有程序都是通过数字逻辑电路执行，如果方案能够同态运算所有的布尔电路，那么就可以密态完成计算机中所有程序及服务。

定义2 C-同态。设C是一个电路集合，HE是一个同态加密方案，任取一个电路Cir∈C，设其输入线有t个。如果对任意的一组明文m1，m2，…，mt和所对应的一组密文 →c=(c1，c2，…，ct)(其中 ci=Encpk(mi))，有下面的等式成立:

则称该方案为C-同态，或者方案对于一个电路集合C是正确的，同时也称C为方案HE的可许电路集合，当C是一个有限电路集合时，也称方案为somewhat同态加密方案。

定义3 紧同态加密。如果存在一个多项式g=g(λ)，使得HE方案的Evaluate算法的输出比特长度不超过g。则称HE是一个紧同态加密方案。

注意:g与所运算的电路Cir、输入密文数无关。表明随着同态操作的进行，密文的尺寸始终保持在一个界之内，其尺寸独立于同态操作数。

定义4 全同态加密方案。一个方案HE对所有的电路既是紧的，又是同态的，则称其是一个全同态加密方案。

定理1自举转化定理。如果一个同态加密方案HE是能够同态计算“自身解密电路”或“解密电路加上额外的门电路”，且满足循环安全，那么该方案可以转化为一个全同态加密方案。

2 DGHV全同态加密方案

本节描述Dijk等人所提出的DGHV方案［7］，其中包括用于构造全同态加密方案的基石—somewhat同态加密方案，和DGHV全同态加密方案。

2． 1 Somewhat同态加密方案

在DGHV方案中需要一些参数来控制各个变量的比特长度，其参数设置为:ρ=λ，ρ'=2λ，η=˜O(λ2)，θ=˜O(λ4)，γ=˜O(λ5)，τ=γ+λ，其中 λ 为安全参数。

首先需要定义一个用于公钥生成的分布，如下:

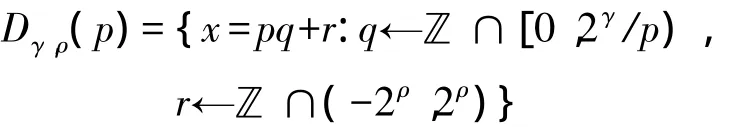
Somewhat同态加密方案 SHE=(KeyGen'，Enc'，Dec'，Evaluate')描述如下:

KeyGen'(λ):根据输入的安全参数λ，随机选择 p←(2ℤ +1)∩［2η-1，2η)。在分布 Dγ，ρ(p)中随机选取 τ+1 个数(x0，x1，…，xτ)，以致 x0为其中最大的数，并x0mod p是偶数。若不满足条件，重新选取直至满足条件。令私钥sk=p，公钥pk=→x=(x0，x1，…，xτ)。

Enc'(pk，m):消息为 m∈{0，1}。随机选择一个整数 r∈(-2ρ'，2ρ')和一个 τ+1 维的比特向量 →v∈{0，1}τ+1。计算密文c=m+2r+2＜→x，→v＞mod x0。

Dec'(sk，c):输出 m'=(c mod p)mod 2。

Evaluate'(pk，C，c1，c2，…，ct):根据输入的公钥pk，布尔算术电路 C，和 t个密文(c1，c2，…，ct)，执行整数上加法和乘法运算。输出电路的结果c'。

该方案的同态操作可以分解为两种基本操作:Add(c0，c1)=c0+c1，Mult(c0，c1)=c0×c1。

2． 2 全同态加密方案

为了将SHE方案转化为全同态加密方案，Dijk等人采用“稀疏子集和”对方案的解密算法进行了压缩，使得方案满足自举性，应用自举转化，从而获得全同态加密方案。其方案FHE=(KeyGen，Enc，Dec，Evaluate)描述如下:

参数选取:κ=γη/ρ'，Θ=ω(κ log λ)，θ=λ。

KeyGen(λ):运行SHE方案的密钥生成算法产生sk=p，pk=→x，设置K=⎿2κ/p⏋，随机选取一个汉明重量 θ的比特向量 →s∈{0，1}Θ，设其指标集为 S={i|si=1}。均匀随机选取 ui∈ℤ ∩［0，2κ+1)，i=0，1，…，Θ-1，使其满足 K=，令 yi=ui/2κ，i=0，1，…，Θ-1，令向量→y=(y0，y1，…，yΘ-1)。输出私钥SK=→s，公钥PK=(→x，→y)。

Enc(PK，m):调用SHE方案生成c=Enc'(pk，m)。然后计算［c·yi］2，i=0，1，…，Θ-1，并对其二进制表达保留小数点后n=logθ+3位的精度，记为zi。得到新密文 ˜c={c，(z0，z1，…，zΘ-1)}。

Evaluate(PK，C，c1，…，ct):将算术电路 C 中的运算替换成整数上加法和乘法运算，每个运算门的输入线上加入解密电路，扩展成增强型解密电路。然后，将密文 c1，c2，…，ct输入到电路中，首先进行重加密(同态解密)操作来更新密文，然后将更新后的密文c'输入到电路门中进行运算，将门输出作为主密文c″，并使用PK中的→y生成对应的其扩展密文 →z″，由此构成密文 ˜c'=(c″，→z″)，如此在电路中运算下去。得到最后的输出。

3 紧致优化技术

由第2节的方案描述可以看出，导致DGHV方案中somewhat同态加密方案密文尺寸增加的原因在于:Add(c0，c1)=c0+c1，Mult(c0，c1)=c0×c1没有进行模操作。因此，文中的初始想法思想为:Add(c0，c1)=(c0+c1)mod x0，Mult(c0，c1)=(c0×c1)mod x0。

计算同态加法和同态乘法，需要进行模x0。但x0中带有随机噪声项r0，模x0将引入一个新的误差。需要对模操作之后的引入噪声进行分析。

1)同态加法:由于两个密文之和不会太大，其和的比特长度与输入密文的尺寸大约一致，模x0只是带入了一个小的x0倍数，可以确定引入的新误差的上界。

2)同态乘法:两个密文之积将变得非常大，其乘积的比特长度大约两倍于输入密文尺寸，模x0运算带入了一个很大的x0倍数，同时带入的新噪声也非常大，无法确定其上界。所以我们对乘法进行优化，确保噪声的可控性。

3． 1 同态操作紧致优化技术

优化过程需要一些辅助数据 x'0，x'1，…，x'γ，其都是非常靠近p的倍数，与方案的公钥相似，但其参数的选取范围不一样，主要在于p的倍式因子q'i的选取。

对同态乘法作修改，c1，c2为两个密文，两个密文相乘之后，按顺序进行分别模 x'γ，x'γ-1，…，x'0。即 opt(c1×c2)=(…(((c1×c2)mod x'γ)mod x'γ-1)…)mod x'0。

优化后的同态操作算法为:Add(c0，c1)=(c0+c1)mod x0，Mult(c0，c1)=opt(c1×c2)。

3． 2 噪声分析

设m1，m2为两个消息比特，由SHE加密算法分别产生其密文c1，c2。

模x0相当于加了一个x0的倍数，则存在两个整数 k1，k2，使得

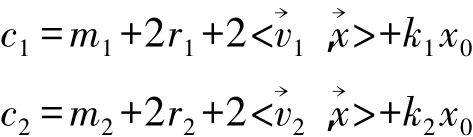
并记两个密文中的噪声为n1，n2。

1)同态加法的噪声分析 SHE．Add(c1，c2):(c1+c2)mod x0

SHE．Add(c1，c2)所获得新密文的噪声为:

2)同态乘法的噪声分析 SHE．Mult(c1，c2):opt(c1×c2)

首先分析模 x'γ所带入的倍数因子 kMult，γ，即(c1×c2)mod x'γ=c1×c2+kMult，γx'γ。

按照优化算法的模顺序，分析在模 x'γ-1过程中，所带入的倍数因子 kMult，γ-1，即如下等式:

同理分析可得|kMult，i|≤2，i=0，1，…，γ-1。

SHE．Mult(c1，c2)所获得新密文的噪声:nMult=那么 |nMult|＜ |n1|· |n2|+(γ+1)·2ρ+1

综上所述，同态加法运算带入的新噪声为2ρ，在同态乘法运算带入的新噪声为(γ+1)·2ρ+1。新的噪声加入，会降低方案的运算能力，下面将对其详细分析，并给出方案的支持同态运算的多项式次数。

3． 3 优化方案的同态运算能力

根据Dijk等人的分析思路，将所需运算的电路C 表示成 t个变元的多项式 f(x1，x2，…，xt)，设其多项式次数为d。这里把SHE能够同态运算多项式次数d作为方案的同态能力指标估计。由文献［7］引理A．1可知，Enc'(pk，m)所产生的新鲜密文的噪声为τ·2ρ+3，并记为X;同态加法中引入的新噪声记为 A=2ρ;同态乘法引入的新噪声记为 B=(γ+1)·2ρ+1。

首先分析一个d次单项式xi1xi2xi3…xid的噪声，由于乘法中噪声变化为|nMult|＜|n1|·|n2|+B。则d次单项式的噪声为:(…(((X·X+B)·X+B)·X+B)…)X+B，归纳得Xd+BXd-2+BXd-3+…+BX+B=Xd+B·(Xd-1-1)/(X-1)。对多项式 f(x1，x2，…，xt)进行放缩处理，将其每一项都放大为一个d次单项式，由于 f(x1，x2，…，xt)一共有‖f‖1项，则将进行‖f‖1-1个同态加法，引入新噪声为(‖f‖1-1)A。综合分析可以得出经过 f(x1，x2，…，xt)同态运算之后的噪声为:‖f‖1(Xd+B·(Xd-1-1)/(X-1))+(‖f‖1-1)A，为了保证解密的正确，噪声上界不能超过p/8。那么可以得到以下等式:

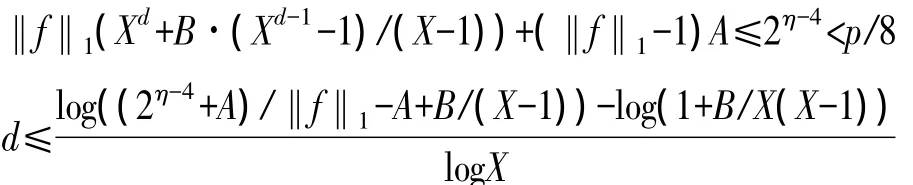
代入 X= τ·2ρ+3，A=2ρ，B=(γ+1)·2ρ+1。B/(X-1)≈(γ+1)/4τ，B/X(X-1)≈(γ+1)/τ2·2ρ+5，忽略此这两项。粗略得到方案的支持同态运算的多项式次数，即同态运算能力为:

4 结语

紧致性是全同态加密方案的必要条件。DGHV方案通过同态解密算法取得整个全同态加密方案的紧致性，导致每个电路输出的密文尺寸为˜O(λ7)。文中在同态操作中引入模运算，并对同态乘法进行优化，使得DGHV方案在同态操作取得紧致性，将密文尺寸控制在˜O(λ5)，但由于需要在同态操作时进行γ个模运算，因此该优化技术增加了同态操作的计算量。再则，文中的紧致性技术使得同态解密算法［8］内部运算中的密文尺寸不增长，这可以使得全同态加密方案中κ的选取由=γη/ρ'变成γ+2，参数设置变得更小。

［1］张盛勇，陈世康．网络编码的安全问题初探［J］．通信技术，2012，45(01):105-107．

ZHANG Sheng-yong，CHEN Shi-kang．Explortion on Security of Network Coding［J］．Communications Technology，2012(01):105-107．

［2］ RIVEST L R，SHAMIR A，ADLEMAN L．A Method for Obtaining Digital Signatures Public Key Cryptosystem［J］．Communication of ACM，1978，21(01):120-126．

［3］ ELGAMAL T．A Public-Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms［J］．Information Theory ，IEEE Transactions，1985，31(04):469-472．

［4］ PAILLIER P．Public-key Cryptosystems based on Composite Degree Residuosity Classes［C］//In J．Stern(Ed．)，EUROCRYPT'99．［s．l．］:Springer，1999:223-238．

［5］ RIVEST L R，ADLEMAN L，DERTOUZOSL M．On Data Banks and Privacy Homomorphisms［C］//In Foundations of Secure Computation．［s．l．］:Academic Press，1978:169-180．

［6］ GENTRY C．Fully Homomorphic Encryption Using Ideal Lattices［C］//In STOC'09．［s．l．］:ACM，2009:169-178．

［7］ DIJK VAN M，GENTRY C，HALEVIS，et al．Fully Homomorphic Encryption over the Integers［C］//In Proc．of Eurocrypt．［s．l．］:Springer，2010:24-43．

［8］汤殿华，祝世雄，曹云飞．整数上全同态加密方案的重加密技术［J］．信息安全与通信保密，2012(01):76-79．

TANG Dian-hua，ZHU Shi-xiong，CAO Yun-fei，Recrypt Technology of A Fully Homomorphic Encryption over Scheme Integers［J］．Information Security and Communictions Privacy，2012(01):76-79．