一种改进的FBD谐波电流检测方法研究

，，

（1.广西龙江电力开发有限责任公司，广西河池 547000；2.山东电力设备有限公司，山东济南 250022；3.广东电网公司韶关供电局，广东韶关 512026）

FBD法是近些年国外学者提出的一种新的时域检测方法。基于传统的瞬时无功功率理论的谐波电流检测和传统的FBD法谐波电流检测均用到了锁相环和低通滤波器，而这两者的使用会使谐波检测的实时性变差。因此本文提出一种新型的FBD谐波电流检测方法，该方法无需锁相环和低通滤波器，而且改进后的FBD法相比传统的瞬时无功功率理论的谐波电流检测和传统的FBD法谐波电流检测动态性能要好。Matlab仿真结果证明了该方法的有效性。

1 FBD检测原理

FBD法是属于时域法范畴的检测方法。FBD法具有良好的实时性，可以应用于单相或多相电路的无功和谐波电流的检测。FBD法是用理想电导元件来等效实际电路中的负载，即认为这个等效电导消耗掉电路中的所有功率，并由此来分解电流。图1为采用FBD法等效的m相实际电路［1-8］。

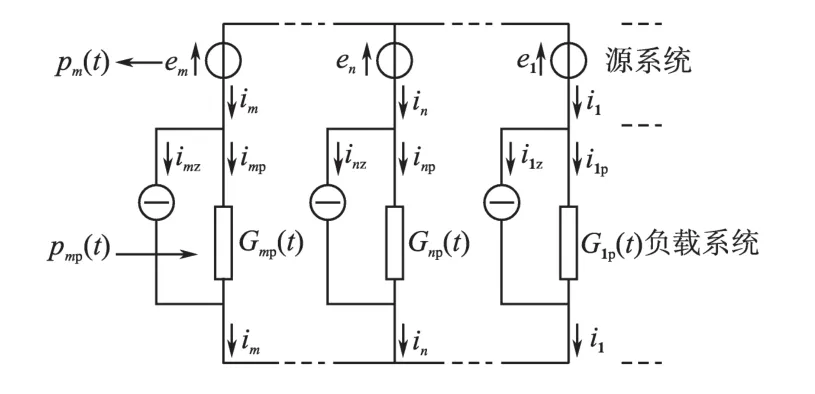
图1 FBD法m相等效电路Fig.1 The m-phase equivalent circuit of FBD method

图1中，系统中电压矢量为：u=(u1,u2,…,um)T＝；系统中电流矢量为：i=(i1,i2,…,im)T；电压和电流矢量中所包含的元素均为瞬时值。负载电流中的有功电流分量为：i1p,i2p,…,imp；负载电流中零功率电流为：i1z,i2z,…,imz；第m相电源系统输出的瞬时功率为：pm(t)。相关定义如下：

瞬时功率为

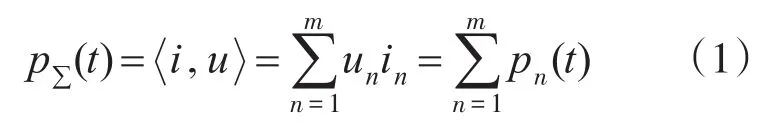
瞬时总电压为

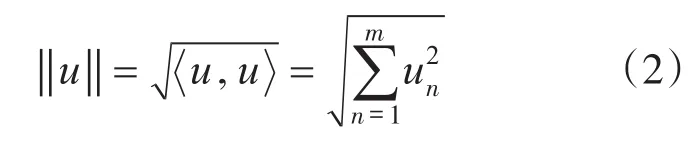
等效有功电导为

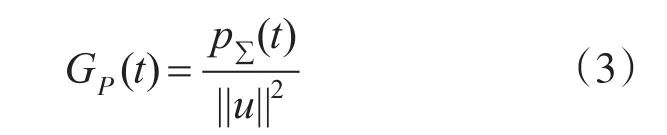
等效有功电导Gp(t)的直流分量Gp为

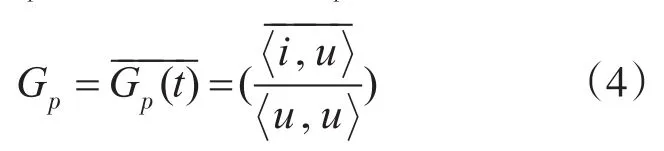
定义线性有功电流为

则等效无功电导为

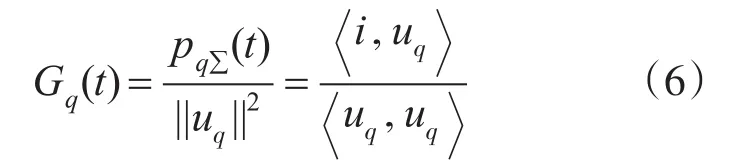
式中：uq为滞后系统电源电压90°的无功电压。

等效无功电导Gq(t)的直流分量Gq为

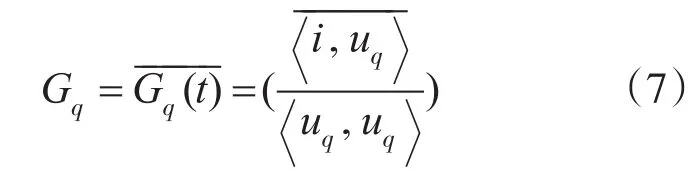
定义线性无功电流为

则系统中的谐波电流分量为

2 传统FBD检测算法

在传统的FBD法和ip-iq法的检测谐波电流中［9-13］，都使用了锁相环输出的与A相电压同相位的正弦、余弦信号。基于ip-iq法和传统FBD法的检测谐波原理图如图2和图3所示。

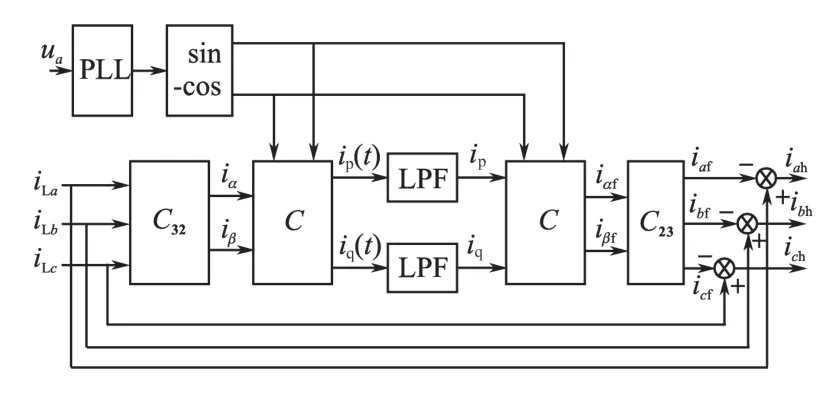
图2 ip-iq法检测谐波原理图Fig.2 Schematic diagram ofip-iqharmonics detection method

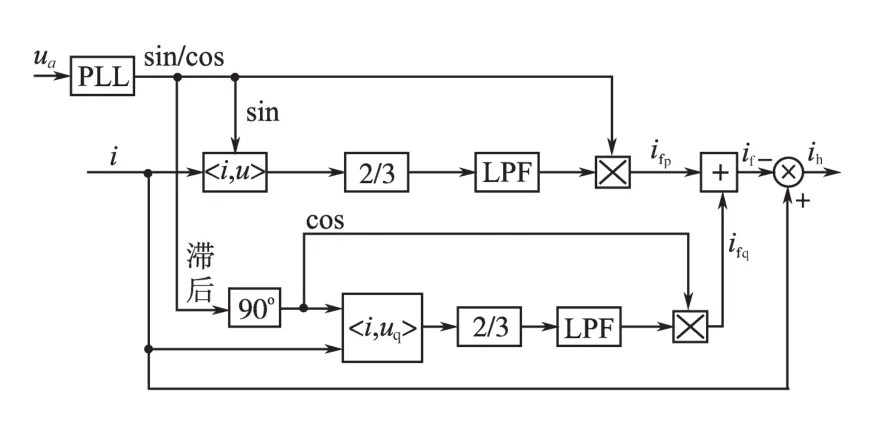
图3 传统FBD法检测谐波原理图Fig.3 Schematic diagram of FBD harmonics detection method

为简化分析，假设系统三相参考电源电压为

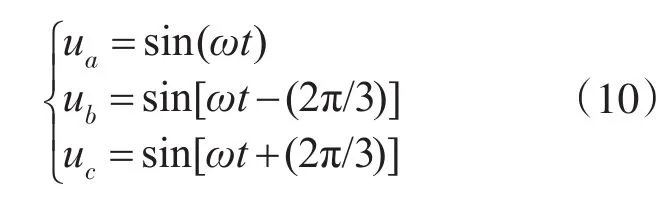
设ia,ib,ic分别为A,B,C三相的负载电流，在ip-iq法中只用于补谐波时，即：

其中

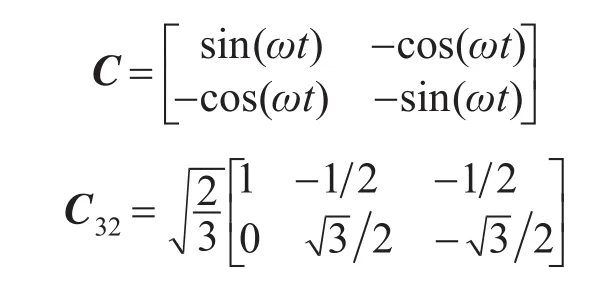
ip(t)，iq(t)经过LPF后就可以得到其直流分量ip，iq，

当系统只补谐波电流时，求得iaf，ibf，icf为

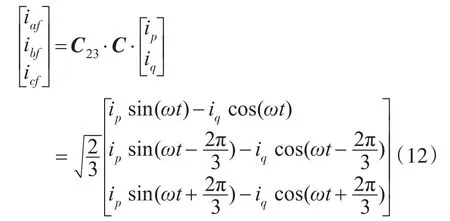
当系统需同时补无功和谐波电流时，只需把iq电流通道断开即可，即：

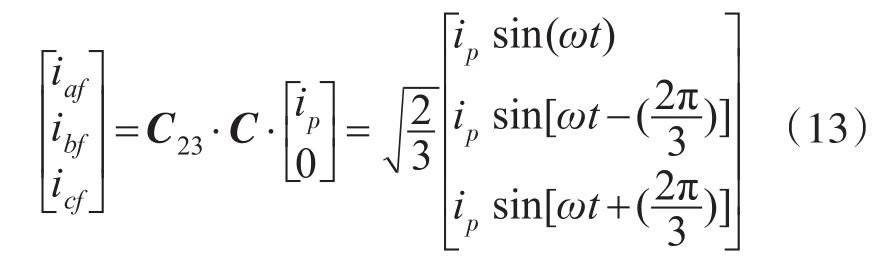
FBD法只用于补谐波时：

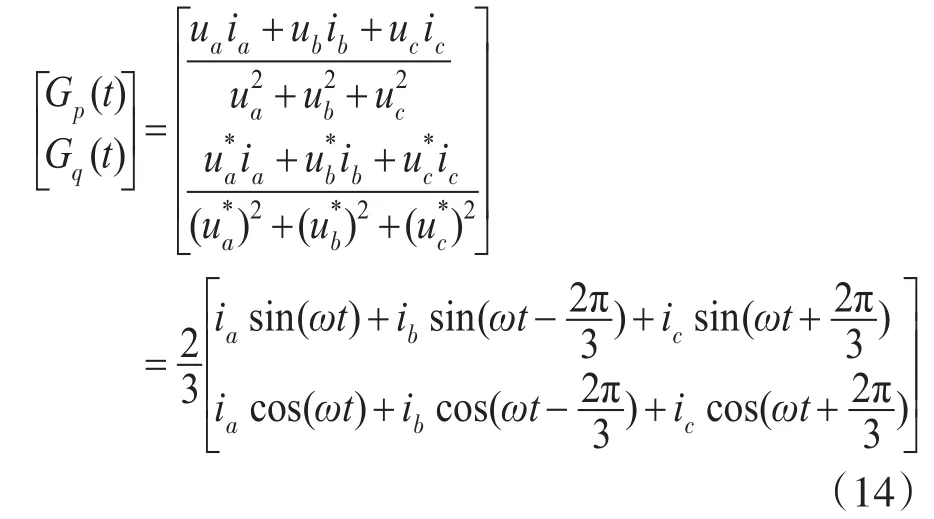
通过对比式（11）、式（14）可得：

Gp(t)，Gq(t)经过LPF后就可以得到其直流分量Gp，Gq为

进而可以得到所需基波电流为

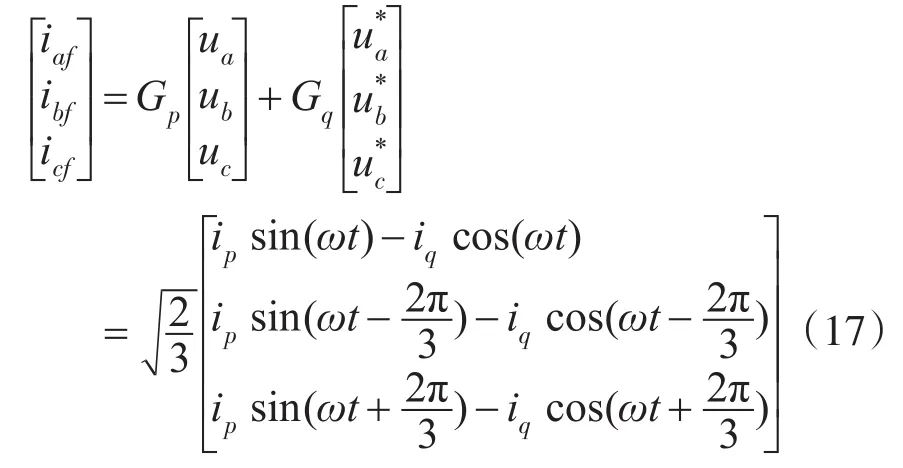
当系统需同时补无功和谐波电流时，只需把

Gq通道断开即可，即：

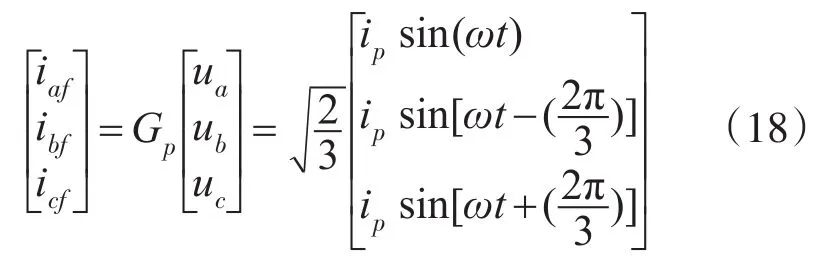
通过观察对比式（12）和式（17），以及式（13）和式（18）可以看出，这两种谐波电流检测方法所得出的结果是一致的。所以传统的FBD法具有与ip-iq一样的检测效果。

在FBD算法中能够很容易地检测出来某指定次数的谐波电流，比如若要检测出第m次谐波电流，即：

设m次谐波的有功电压为

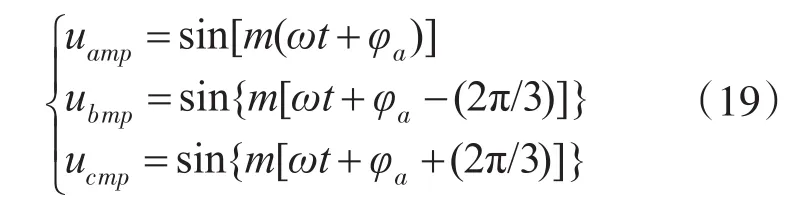
m次谐波的无功电压为

然后重复上述的计算过程即可求出所需的谐波分量。

3 改进的FBD检测算法

通过上面的分析可知，传统的FBD法和ip-iq法在进行谐波检测时需要用到锁相环和低通滤波器，然而两者会对谐波检测造成一定的延时，且当电网电压波动较严重时，锁相环就不能够准确地锁住A相电压的相位，进而造成检测结果的不准确。所以本文提出一种无需锁相环和低通滤波器的改进型FBD谐波检测算法，该谐波检测方法是基于虚拟磁链观测方法的基础上，通过电网虚拟磁链角与电网三相电压相位之间的关系重构出单位幅值的三相电压，从而省去了电网电压锁相环节。改进型FBD谐波检测原理框图如图4所示［14-18］。

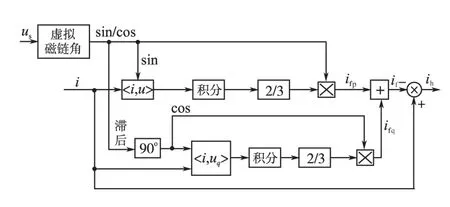
图4 新型的FBD谐波电流检测算法Fig.4 Improved FBD harmonic detecting method

3.1 基于虚拟磁链的无锁相环控制

本改进FBD谐波检测方法实现无锁相环的核心是得到虚拟磁链矢量Ψ的空间位置角θ。由电压矢量e与旋转虚拟磁链矢量Ψ的关系：Ψ=∫edt，可以得出αβ坐标系中电网侧的磁链为

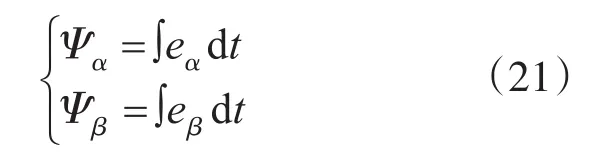
式中：eα，eβ分别为三相系统电压矢量在α，β轴上的分量；Ψα，Ψβ分别为虚拟磁链矢量Ψ在α，β轴上的分量。则可得：

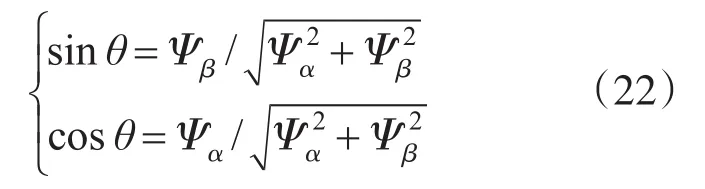
因此θ为

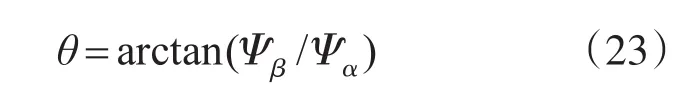
定义电压矢量幅角为φe。由于电压矢量e在旋转坐标系中是按照角速度ω逆时针旋转的，所以可以得出φe与ω的关系为

进而可得虚拟磁链角θ与A相电压相位ωt的关系为：ωt=θ+π；可以重构出来的单位幅值的三相电源电压如下：

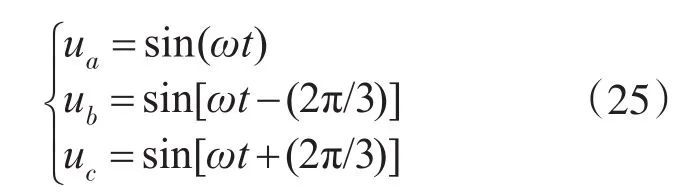
3.2 基于积分的低通滤波控制

积分具有低通滤波器的特性，系统中的谐波在经过纯积分器后，K次谐波电压的幅值以基波的K倍衰减，对于高次谐波有一定的滤除作用。

而在本文中积分的输入是三相电路的瞬时功率，通过积分环节后即得到3项瞬时功率的平均值，而瞬时功率平均值即为负载电流中基波电流正序分量的瞬时功率，所以通过积分环节后即把高次谐波电流分量的功率分量进行了滤除。

如果用纯积分的方法计算因存在积分初值问题，会造成一定的偏差，若输入正弦信号的峰值不是初值的话，就会在积分出来的余弦信号上叠加一个直流分量，这会很容易造成积分器饱和现象。

在传统的解决纯积分器所带来的初值问题中，经常会使用一阶惯性滤波器1/(s+ωf)，来代替，从一阶惯性LPF的公式来看，当输入的频率ω远大于ωf时，此时才能够等效为，但为了使直流分量的衰减不至于太慢，所以要求ωf不能很小，要有一定值；因此一阶惯性LPF就存在一定的矛盾：要使直流分量衰减，则ωf必须保持定值；要近似等效为纯积分器就要使ωf远小于ω。

因此本文采用2个低通滤波器来替代纯积分器［19］，可以使得幅值和相角无偏差。即：

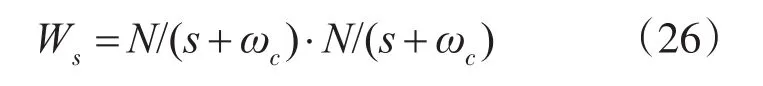
正弦信号sin(ωct)经纯积分环节后会得到一个幅值为原来幅值1/ωc且相位滞后90°的余弦信号。采用2个低通滤波器级联相乘后，为了使其具有相同的时间常数，使其具有积分的效果。则根据相角条件可得：

根据幅值无衰减可得：

由此可得：

图5所示为给出的正弦信号经纯积分环节和2个一阶低通滤波器环节的结果。图5a为输入的正弦信号，图5b为分别经过2个环节后的结果比较，从图5b中可以看出纯积分环节发生了直流偏移现象。且图5b中2个波形实际的幅值都衰减为原来幅值的，所以在图5b中所观察的2个信号为都乘314后的。

图5 两种观测器性能比较Fig.5 Comparison of the two observers

4 仿真分析及结论

为了验证所提出的改进型FBD法谐波检测方法的实时性与有效性，进行了仿真分析，仿真参数如下：A相电压=（220∠0°）V，B相电压=（220∠-120°）V，C相电压=（220∠120°）V，负载电阻R=8Ω，负载电感L=1 mH。虚拟磁链定向角如图6所示；采用3种方法检测出的基波正序电流如图7所示。

为了体现改进型FBD检测方法在电网电压畸变时的检测性能，在0.1 s时向三相电网电压上加入3次和5次谐波电压；图8即为改进型FBD法在电网电压畸变情况下的仿真结果，从图8中可以看出所提出的改进型FBD检测方法仍能够准确地检测出基波正序电流。

图6 虚拟磁链定向角Fig.6 Virtual flux orientation angle

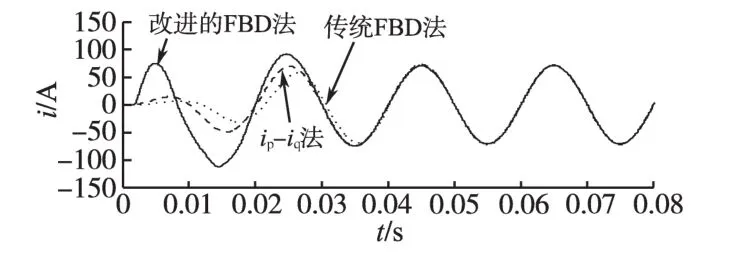
图7 采用3种方法检测出的基波正序电流Fig.7 Fundamental positive sequence currents detected by the three methods

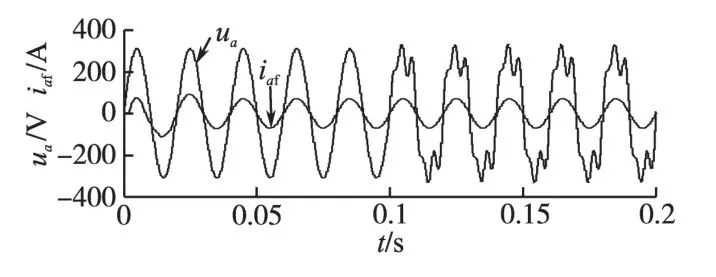
图8 基于改进型FBD检测算法的仿真结果Fig.8 Simulation results with the improved FBD harmonic detecting algorithm

利用Matlab对负载电流中的5次和7次谐波电流分量进行仿真，从图9中可以看出，FBD法能够准确地检测出5次和7次谐波，负载电流中5次和7次谐波电流分量分别为16.08 A和8.12 A。

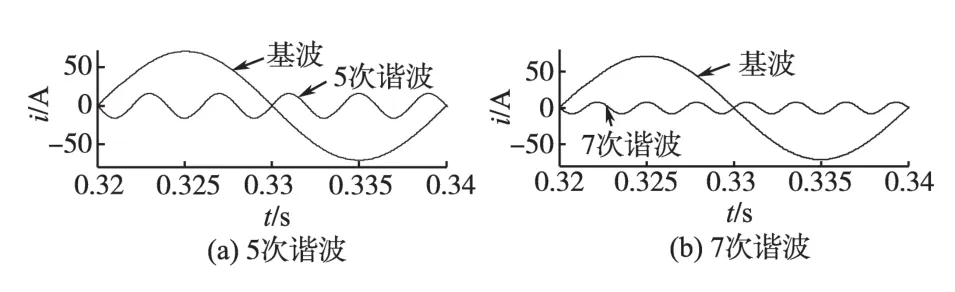
图9 FBD指定次数谐波电流检测Fig.9 Selected harmonic detection by FBD method

本文提出了基于虚拟磁链观测的无锁相环FBD改进谐波检测算法，并用2个一阶低通滤波器来取代检测算法当中的纯积分环节，通过仿真验证该方法能够很好地解决纯积分环节造成的幅值衰减和相移问题，同时也提高了改进FBD谐波检测算法的精度。

［1］陈峻岭，姜新建，孙卓，等.基于FBD法的三相电力系统电流检测方法的应用［J］.电力系统自动化，2004：28（24）：23-27.

［2］王杰，申张亮.基于FBD法的四相输电系统电流检测方法［J］.中国电机工程学报，2007，27（22）：87-93.

［3］康静，郑建勇，曾伟，等.FBD法在三相四线制系统电流实时检测中应用［J］.电力自动化设备，2006，26（8）：36-39.

［4］伏祥运，代鹏.FBD功率理论在无功补偿器控制中的应用［J］.江苏电机工程，2009，28（1）：39-42.

［5］丁祖军，郑建勇，胡敏强，等.FBD算法电流检测的滞后误差建模［J］.电工技术学报，2008，23（2）：133-137.

［6］程琼，郑建勇.三相电力系统电流检测方法FBD法的研究［J］.湖北工业大学学报，2008，23（1）：49-52.

［7］伏祥运，王建赜，纪延超.不对称系统中基于FBD理论的无功电流快速检测方法［J］.电力自动化设备，2007，27（3）：30-33.

［8］刘宏超，吕胜民，张春晖，等.采用FBD电流检测法的三相四线法APF［J］.电力自动化设备，2010，30（1）：45-48.

［9］王杰，申张亮.基于FBD谐波检测方法的有源电力滤波器系统设计［J］.电工电气，2010（8）：9-13.

［10］黄宇淇，孙卓，姜新建，等.FBD法及复合控制在有源滤波器中的应用［J］.电力系统自动化，2006，30（7）：65-68.

［11］陈娟，郑建勇，丁祖军，等.p-q-r法与FBD法在三相四线制系统谐波电流检测中的对比［J］.电力自动化设备，2007，27（11）：30-33.

［12］吴峰，郑建勇，梅军.谐波电流检测技术的理论与FBD法仿真试验研究［J］.低压电器，2011（15）：45-50.

［13］时国平，许卫兵，王长春.基于FBD法的三相四桥臂APF的研究［J］.自动化与仪器仪表，2010（5）：22-24.

［14］Xu Y，Tolbert L M，Chiasson J N，et al.A Generalised Instantaneous Non-active Power Theory for Statcom[J].IET Electr.Power Appl.，2007，1（6）：853-861.

［15］Rafael Ordoñez，Roberto Morales，Charif Karimi.Three-phase Active Power Filter Under Non-sinusoidal Voltage Conditions：2009 International Conference on Electrical[C]//Communications，and Computers，2009：69-73.

［16］Helmo K M Paredes，Fernando P Marafão，Luiz C P da Silva.A Comparative Analysis of FBD，PQandCPTCurrentDecompositions-Part I：Three-phase Three-wire Systems[C]//2009 IEEE Bucharest Power Tech Conference，June 28th-July 2nd，Bucharest，Romania，2009.

［17］YANG Chao，HUANG Qingxiu，ZHOU Jiangman.Research of Hybrid Active Power Filter Based on FBD Method Detection[C]//IEEE，2011：4205-4208.

［18］Helmo K M Paredes，Fernando P Marafão，Luiz C P da Silva.A Comparative Analysis of FBD，PQ and CPT Current Decompositions-part II：Three-phase Four-wire Systems[C]//2009 IEEE Bucharest Power Tech Conference，June 28th-July 2nd，Bucharest，Romania，2009.

［19］吴轩钦，谭国俊，张倩倩，等.新颖虚拟电网磁链在有源滤波器中的应用［J］.电力系统及其自动化学报，2010，22（6）：77-82.