致密砂岩和页岩渗透率实验研究

陈志明，汪伟英，蔡雨桐，刘冰

（长江大学石油工程学院，湖北 荆州 434023）

致密砂岩气和页岩气是潜力巨大的非常规天然气资源，具有广阔的开发前景［1-2］，近年来在天然气产量中的比例不断加大，占有越来越重要的地位。准确测定致密砂岩和页岩渗透率，对研究其渗流规律具有重要意义。对于中、高渗储层，一般基于达西公式应用岩心流动实验，进行岩石渗透率的确定；然而对于低渗储层，由于岩石渗透率极低，在岩心流动实验过程中，需要很长时间才能达到稳定状态，这使得实验数据难以准确测得，实验精度不能得到保证［3］。因此，用常规方法准确测量致密砂岩和页岩渗透率，成为国内外学者普遍认为的一大难题［4-5］。本文介绍了一种新的实验研究方法，用以准确测定致密砂岩和页岩的渗透率。

1 实验原理

Brace等［6］在测量花岗岩渗透率的实验过程中，建立了可压缩流体在饱和均质孔隙中的单向流模型：

Hsieh 等［7］和 Dicker等［8］提出了单向流模型式（1）的可行解，为容器两端的无量纲化压差δpD关于时间t的函数，表达式为

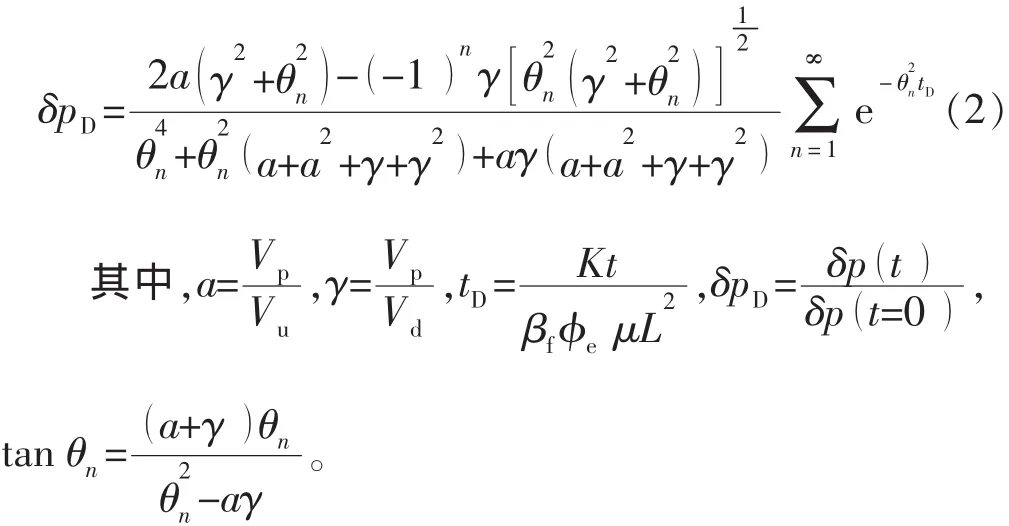
Kamath等［9］研究表明：如果采用小体积容器测定致密砂岩和页岩的渗透率，会产生较大误差；另外，由于页岩对流体具有一定的吸附作用［10-11］，会使渗透率的测量值偏低。因此，为消除由小体积和吸附效应等因素引起的误差［12］。

本实验在岩样上端建立了一个体积无穷大、并维持恒压的容器，则Vu=∞，a=VpVu=0，从而可以把可行解式（2）简化为

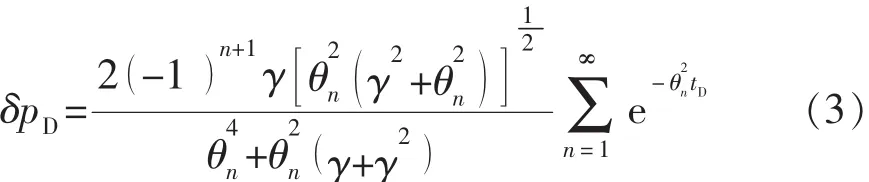
又假设流体以很大的流度进入岩样，使渗流瞬时满足达西定律，则式（3）可以简化为单一的指数形式，即，n=1，θn=θ。因此，可以得出：

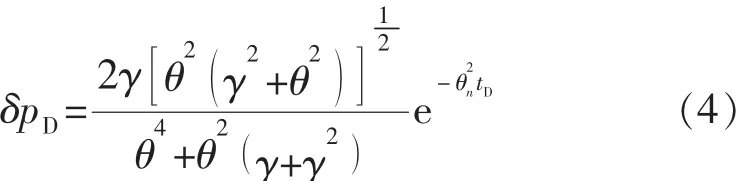
对式（6）两端同时取自然对数，为方便作图，将其转换为常用对数：

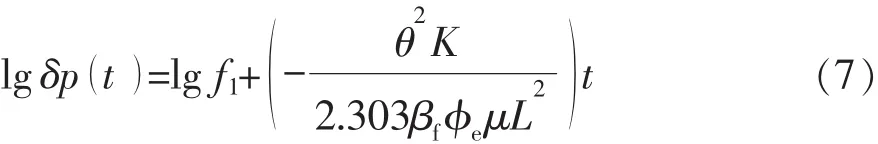
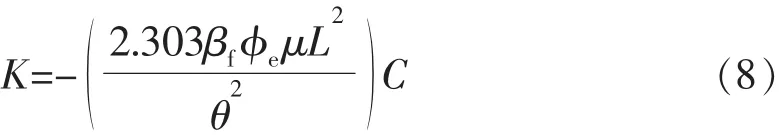
2 实验装置

实验装置由上端、下端和围压3种静压装置组成（见图1）。上端容器的压力由压力传感器控制和监测，两端容器压差由另一压力传感器记录。容器、阀门和压力传感器都置于恒温箱中，恒温箱的温度波动范围在±0.1℃，48 h内恒温箱温度绝对偏差小于0.2℃。压力由注入泵组控制，其中一个施加围压，一个控制上端压力，一组控制岩样下端与各管路之间的压力差。泵全部位于恒温箱之外，但涂有绝热材料。实验注入速度为1.67×10-13～3.0×10-5m3/min，并通过 RS-232 接口与计算机连接，以记录注入数据。

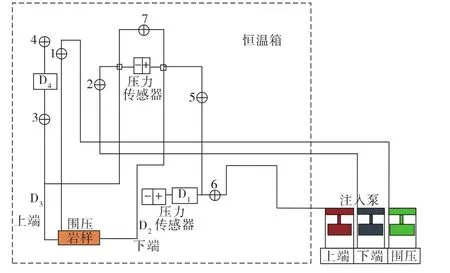
图1 实验装置示意

3 实验内容

3.1 实验准备

实验前，制作若干个直径为2.54 cm、长为5.08 cm的致密砂岩及天然、人工页岩岩心；用砂纸将岩块表面打磨光滑并洗净；置于真空度为0.08 MPa、温度为100℃的恒温箱内5～8 h；待自由水烘干后，放在干燥器中冷却30 min。

实验时，将岩心抽空，饱和实验流体；将饱和实验流体的岩心置于岩心夹持器中；让注入泵正常工作，并利用压力传感器监测压力数据，计算机记录注入泵的数据。实验温度为25℃，利用模拟地层水和氮气对页岩的渗透率进行测量。

3.2 参数测量

由实验原理可知，根据对数曲线的斜率式（8）可计算出渗透率，岩心长度已知，因此，只需要测量流体的压缩系数、黏度及岩心的有效孔隙度。

3.2.1 流体压缩系数

当实验流体为液体时，利用容器体积改变量δV、压力改变量δp和原始体积V0，就可以计算出液体的压缩系数 βl：

另外，也可以利用恒压模型（δp=0），通过注入过程中计算机记录的泵体积变化值，得到流体压缩系数。该方法的优点是在任意压力下，都可以测量出流体的压缩系数。而当实验流体为气体时［13］，气体的压缩系数为

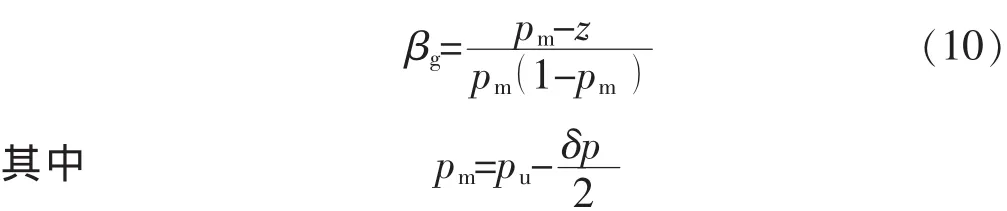
该实验利用氮气测量岩心的气体渗透率，由SUPERTAATM软件和 P-R 状态方程［14］，计算氮气在25℃、不同压力下的压缩系数。

3.2.2 有效孔隙度

在实验初始条件下，氮气的压力为p1，氮气体积为VN，容器的体积分别为Vd，Vu，孔隙体积为Vp。 当扩散达到稳定状态后，测得的系统压力为p2，利用玻义尔定律［15］可计算出孔隙体积：

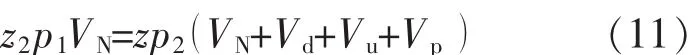
由于Vp对孔隙压力、温度较敏感，因此将测量装置放在恒温箱中。另外，岩样的骨架体积Vb可以通过直径和长度测量，则有效孔隙度为

3.2.3 黏度

对于液体，在恒温条件下，黏度与压力无关（高压条件下除外）。因此，该实验利用黏度为1 mPa·s的模拟地层水作为渗流介质。由于气体黏度与压力有关，实验利用SUPERTAATM软件，在25℃、不同压力条件下计算出了氮气的黏度。

3.3 渗透率计算

由测得的实验数据绘制δp-t关系曲线（见图2），对曲线进行拟合，得到曲线斜率C。由tan θ=γ/θ和γ=Vp/Vd可计算得出θ，结合实验测得的流体压缩系数βf、黏度μ、岩心长度L及有效孔隙度φe，利用式（8），可求出岩心的渗透率。

图2 容器两端压差随时间的变化关系

3.4 误差分析

实验误差分析表明：

1）岩心中压力梯度为常数，实际上岩心是非均质的，这就使实验产生了误差，但是，如果岩样的孔隙体积与末端容器体积之比小于0.1，这种误差就会小于1%［16］；

2）实验采用恒压无限大的上端容器模型，可以忽略由吸附效应引起的误差；

3）实验通过恒温箱控制温度，可以减小由于温度引起的误差；

4）实验通过不同的压力传感器记录压力，可以减小仪器的误差；

5）由于致密砂岩和页岩的渗透率对围压很敏感，实验过程中围压的波动范围就应该控制在0.003 MPa以内。

忽略其他因素引起的误差（如容器的绝对体积及压缩系数等），认为本实验的误差较小，实验精度较高，结果可靠。

4 结果与讨论

4.1 渗透率测量结果

该实验利用模拟地层水和氮气，对不同致密砂岩、天然和人工页岩岩心进行了渗透率测量，并与美国岩心公司生产的CMS300和PDP250仪的测量结果进行了比较（见表 1、表 2）。

表1为致密砂岩的岩心液测渗透率与CMS300仪渗透率测试数据；表2为天然和人工页岩的岩心气测渗透率与PDP250仪渗透率测试数据。结果表明，岩心实验与CMS300仪测量的液测渗透率平均相差9.23%，与PDP250仪测量的气测渗透率平均相差11.88%，说明实验结果具有一定的可靠性。

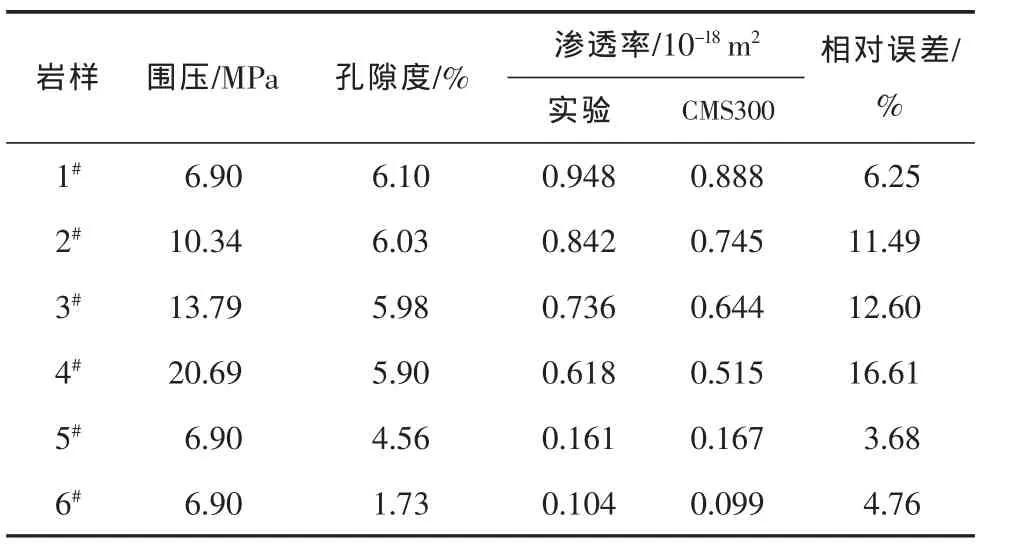
表1 致密砂岩岩心实验与CMS300仪所测渗透率对比

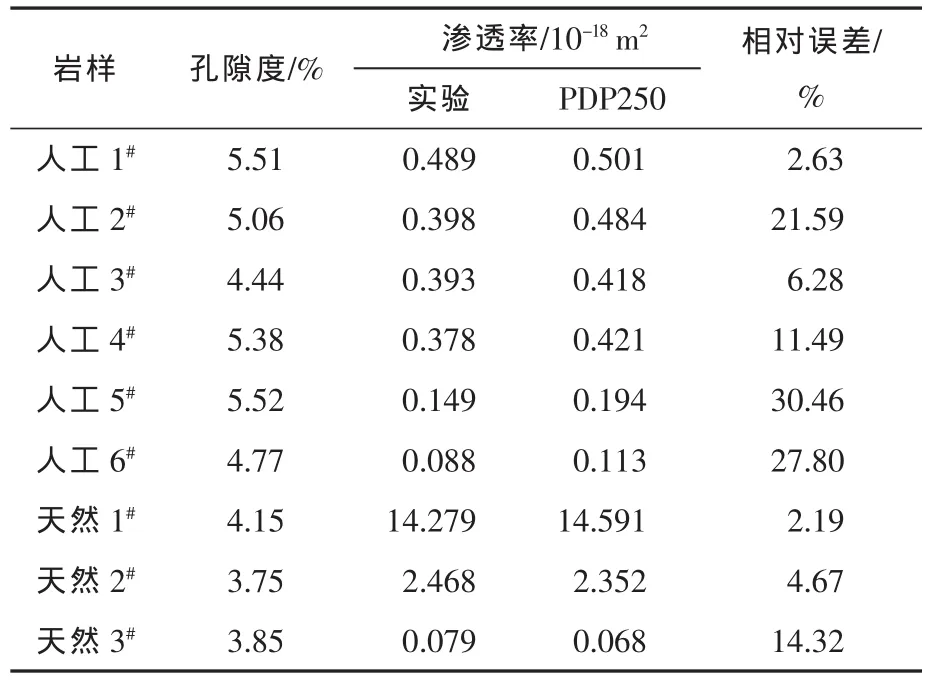
表2 页岩岩心实验与PDP250仪所测渗透率对比

4.2 渗透率与有效压力的关系

实验测得不同有效压力条件下致密砂岩和页岩的渗透率，渗透率与有效压力的关系见图3。

从图3可以看出，实验岩样的渗透率随着有效压力的增加，呈非线性减小。

经回归拟合，关系式如下：

分析认为，由于致密砂岩和页岩具有低孔、低渗的特性，岩石孔隙结构十分复杂，所以，在研究其渗透率时，不能简单地用毛细管束模型描述岩石结构，而需要用网络模型解释。

随着有效压力的增加，在流动网络中起重要作用的孔隙体积减小，就会对渗流产生明显的影响；因此，渗透率随着有效压力的增加而表现出非线性减小，就可以用对数关系进行描述，这与一些学者［17-20］的研究结果吻合较好。

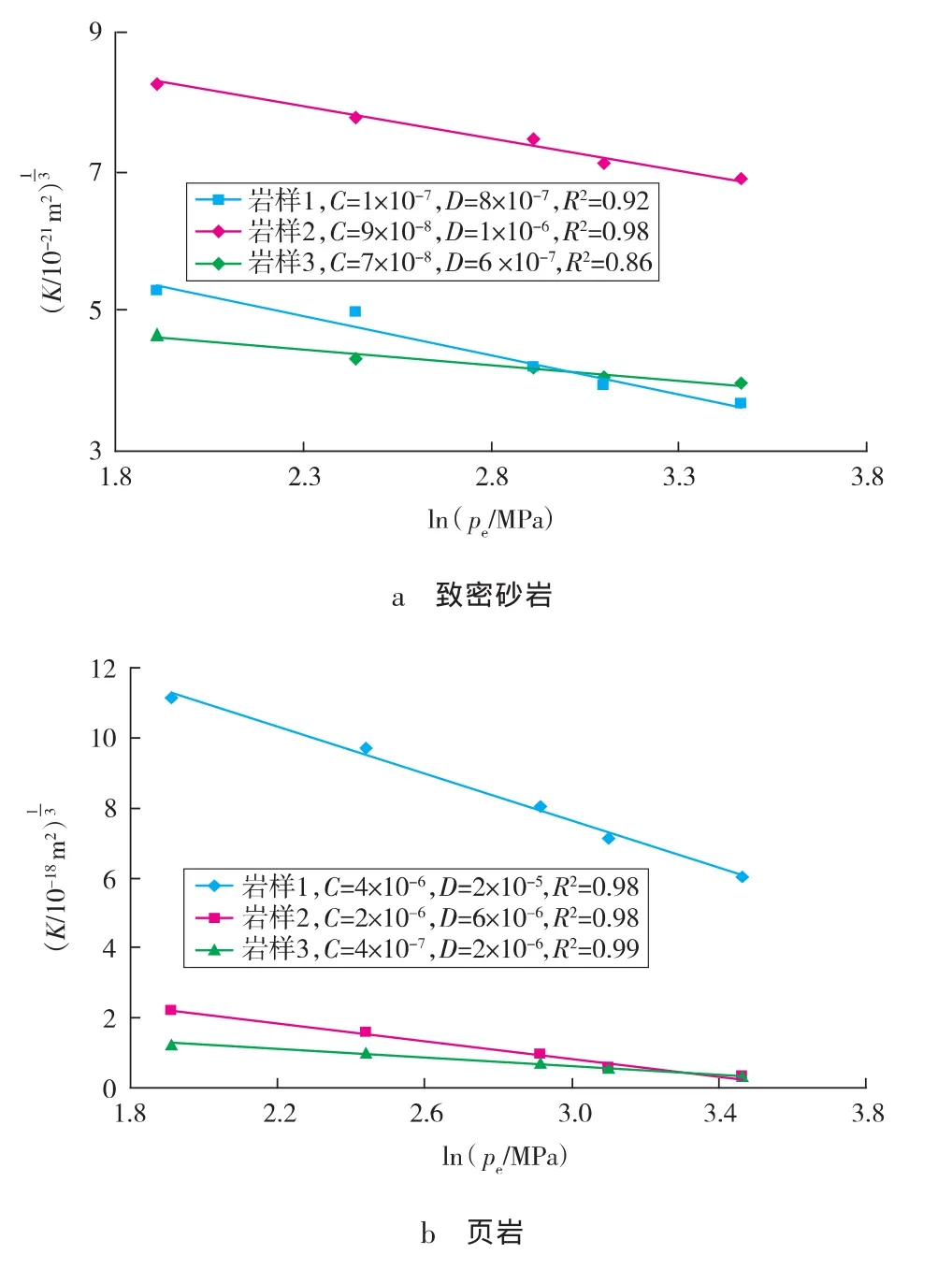
图3与lnpe的关系

5 结论

1）对岩心的非均质性、吸附效应以及实验温度、仪器和围压等因素可能引起的实验误差进行了分析，结果表明实验误差较小。

2）在不同条件下测量了岩心的气体和液体渗透率，并与美国岩心公司生产的CMS300仪和PDP250仪测量结果进行了对比，其差值在允许范围内，说明实验测量结果具有一定的可靠性。

3）通过实验得出了致密砂岩和页岩渗透率与有效压力之间的关系：渗透率随着有效压力的增加而呈非线性减小，页岩的减小幅度较致密砂岩大。同时，建立的关系方程与实验数据具有很好的吻合性，拟合相关系数高达0.98以上，说明该实验方法和建立的方程是合理的。

6 符号注释

k 为水的传导率，m/s；p 为压力，MPa；Ss为岩样的比容量，MPa-1；K 为岩样渗透率，m2；ρ为流体密度，kg/m3；g 为重力加速度，m/s2；μ 为流体黏度，Pa·s；βeff，βs，βf，βl，βg分别为岩石有效压缩系数、 岩石骨架压缩系数、流体的压缩系数、液体的压缩系数及气体的压缩系数，MPa-1；φe为有效孔隙度，%；δpD为压差比，无量纲；a为岩样孔隙体积与上端容器体积比值，无量纲；γ为岩样孔隙体积与下端容器体积比值，无量纲；VN，Vp，Vu，Vd，Vb分别为氮气体积、孔隙体积、岩样上端容器体积、岩样下端容器体积及岩石骨架体积，m3；L为岩样长度，cm；δp（t），δp（t=0），δp 分别为 t时刻两端容器的压差、两端容器初始压差、pu与pd的压差，MPa；C为斜率；D为截距，常数；δV为容器体积改变量，m3；z为气体的压缩因子，无量纲；pm，pu，pd分别为平均孔隙压力、上端容器压力和下端容器压力，MPa。

［1］陈会年，张卫东，谢麟元，等.世界非常规天然气的储量及开采现状［J］.断块油气田，2010，17（4）：439-442.

［2］卢占国，李强，李建兵，等.页岩储层伤害机理研究进展［J］.断块油气田，2012，19（5）：629-633.

［3］陈志明，蔡雨桐，刘冰，等.低渗透岩石渗流规律的实验研究方法［J］.天然气与石油，2012，30（3）：49-52.

［4］李智锋，李治平，王杨，等.页岩气储层渗透性测试方法对比分析［J］.断块油气田，2011，18（6）：761-764.

［5］杨茜，付玲.致密砂岩气的成藏机理及勘探前景［J］.断块油气田，2012，19（3）：302-306.

［6］Brace W F，Walsh J B，Frangos W T.Permeability of granite under high pressure［J］.J.Geophys.Res.，1968，73（6）：2225-2236.

［7］Hsieh P A，Tracy J V.A transient laboratory method for determining the hydraulic properties of tight rocks［J］.International Journal of Rock Mechanics and Mining Sciences and Geo-Mechanics Abstracts，1981，18 （3）：245-252.

［8］Dicker A I，Smits R M.A practical approach for determining permeability from laboratory pressure-pulse decay measurements［R］.SPE 17578，1988.

［9］Kamath J，Boyer R E，Nakagawa F M.Characterization of core-scale heterogeneities using laboratory pressure transients［J］.SPE Formation Evaluation，1992，1（3）：219-227.

［10］关富佳，吴恩江，邱争科，等.页岩气渗流机理对气藏开采的影响［J］.大庆石油地质与开发，2011，30（2）：80-83.

［11］梁超，姜在兴，郭岭，等.黔北地区下寒武统黑色页岩沉积特征及页岩气意义［J］.断块油气田，2012，19（1）：22-26.

［12］Cui X，Bustin M M A，Bustin M R.Measuring of gas permeability and diffusivity of tight reservoir rocks：Different approaches and their applications［J］.Geo-Fluids，2009（9）：208-223.

［13］Walder J，Nur A.Permeability measurement by pulse-decay method：effects of poroelastic phenomena and nonlinear pore pressure diffusion［J］.International Journal of Rock Mechanics and Mining Sciences and Geo-Mechanics Abstracts，1986，23（3）：225-232.

［14］Peng D Y，Robinson D B.A new two-constant equation of state［J］.Ind.Eng.Chem.Fundam.，1976，15（1）：59-64.

［15］杨胜来，魏俊之.油层物理学［M］.北京：石油工业出版社，2004：125-127.

［16］Trimmer D.Design criteria for laboratory measurements of low permeability rocks［J］.Geophys.Res.Lett.，1981，8（9）：973-975.

［17］Jones F O，Owens W W.A laboratory study of low permeability gas sands［R］.SPE 7551，1979.

［18］庞长英，连军利，吴一凡，等.美国页岩油气开发技术及对我国的启示［J］.石油地质与工程，2012，26（5）：62-66.

［19］Ostensen R W.Microcrack permeability in tight gas sandstone［J］.SPE Journal，1983，23（6）：919-927.

［20］熊健，郭平，张涛.特低渗透岩心相对渗透率实验研究［J］.石油地质与工程，2011，25（3）：111-113，116.