一种基于Boosting的目标识别方法

肖秦琨，钱春虎，高嵩

（1.西安工业大学 电子信息工程学院，陕西 西安 710032）

0 引言

在机器学习领域中，如何通过观测数据的学习得到精确估计是一个关键问题。而在实际应用领域中，构造一个高精度的估计是很困难的。Boosting是一种试图提高任意给定学习算法精度的方法。它的思想起源 Valiant［1］提出的 PAC（Probably Approximately Correct）学习模型。PAC（概率近似正确）是统计机器学习、集成机器学习等方法的理论基础。此后很多学者开始了PAC学习模型的研究。Kearns和Valiant首次提出了PAC学习模型中弱学习算法和强学习算法的等价性问题［2］，即是否可以将弱学习算法提升为强学习算法?如果两者等价，那么只需找到一个比随机猜测略好的弱学习算法，就可以将其提升为强学习算法，而不必寻找通常条件下很难获得的强学习算法。1990年Schapire［3］最先提出了一种可证明的多项式时间Boosting算法，对上述问题做出了肯定的回答。一年后，Freund［4］设计了一种通过重取样或过滤运作的高效的BBM（Boost－by－majority）算法。但这两种算法在实践上存在着缺陷，那就是都必须事先知道弱学习算法学习正确率的下限。1995年Freund与Schapire［5］对Boosting算法进行了改进，提出了 AdaBoost（Adaptive Boosting）算法。这个算法和BBM算法的效率几乎一样，但不需要任何关于弱学习器的先验知识，所以容易应用到实际问题中去。然后，Boosting算法经过进一步改进又有了新的突破，如通过调整权重而运作的Ada-Boost.M1、AdaBoost.M2、AdaBoost.R 算法等，解决了早期的 Boosting算法很多实践上的问题［6］。

和其他算法相比较，Boosting算法有很多优点:（1）在分类的同时能够进行特征选取，编程容易，速度快、简单;（2）只要给定足够多的数据，Boosting不需要弱分类器的先验知识，只需要通过寻找比随机稍好的弱分类器，就能最终得到一个比较好的强分类器;（3）在弱分类器确定后，除了迭代次数T之外，其他参数都不需要调节;（4）能够得到算法的误差上界。

1 算法描述

算法示意图如图1所示。算法的基本思想如下:（1）采用Gentle Adaboost算法进行目标识别，Gentle Adaboost算法是Friedman［7］等在1998年提出的，它是对Boosting算法的改进。首先任意给一个弱学习算法和训练集（x1，y1）…，（xn，yn），此处，xi∈X表示某个域或实例空间，yi是xi的类别标识，且满足yi=f（xi），且yi∈Y={+1，－1}。设迭代次数为 t，t=1，2…T，设第 t轮迭代时第i个训练样本（xi，yi）分布的权重记为wt（i），Gentle Adaboost算法在每轮迭代时反复调用给定的弱学习算法。初始化时，每个训练样本的权重均为w1（i）=1。接着，调用弱学习算法进行T次迭代，每次迭代后按训练结果来更新训练集上的分布，对训练失败的训练样本赋予较大的权重，使得下一次对这些训练样本更加关注，从而也得到一个预测序列h1，h2…，hT。T次迭代后，在分类问题中最终的预测函数H（x）采用有权重的投票方式产生，其中H（x）可以这样表示:

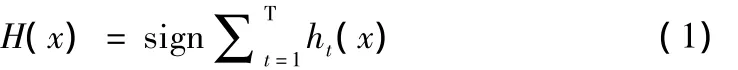
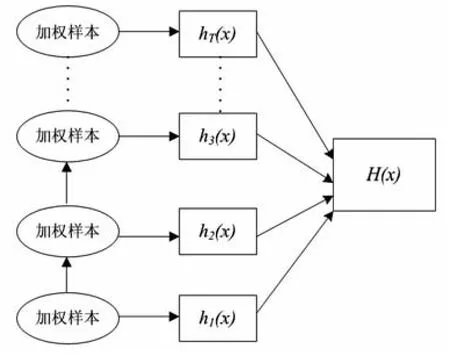
图1 Boosting算法示意图

算法步骤如下:

（1）给定样本（x1，y1），…，（xn，yn），背景样本 yi= －1，目标样本yi=1;

（2）创建图像集:从LabelMe中选择含有car类目标的图像200幅作为训练集，若干幅图像作为测试集;

（3）图像预处理:对训练/测试图像和目标进行归一化处理，训练图像大小为［128 200］，测试图像大小为［256 256］;

（4）创建特征库:选择8幅图像建立特征库，提取20个目标掩膜边缘取样点和目标中心的位置，每幅图像经过4种用于图像边缘增强的滤波器，得到640个图像片段gf，将得到的特征块（Patches）存储到特征库中;

（5）计算特征:利用创建的特征库片段gf、片段gf的位置wf来计算训练样本的特征值，

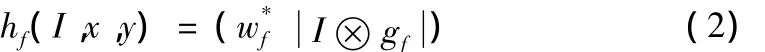
其中*表示卷积算子，⊗表示归一化互相关，对wf的卷积用来确定图像片段是否出现在期望位置上，从中找出背景样本和目标样本的位置;

（6）采用Gentle Adaboost算法来训练检测器，流程图如图2所示:

① 设迭代次数为 t，t=1，2…T，第 i个训练样本（xi，yi）分布的权重记为wi，初始化权值为wi=1，

其中 i=1，2…n，H（x）=0;

② 设置弱分类器:

ht（x）由四个参数［a，b，θ，k］来决定，对正确分类（xk≥θ）赋予权值 a，其中 t=1，2…T;

采用公式（4）对每个样本更新权值:

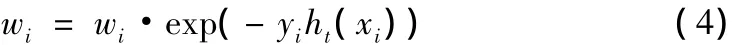
其中，yi为输出期望，i=1，2…n;

采用公式（5）对每个样本更新分类器:

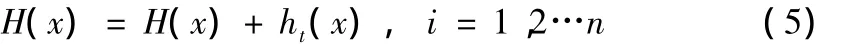
③输出强分类器:H（x）由公式（1）得出。当x≥0，sign（x）为1，否则为－1;

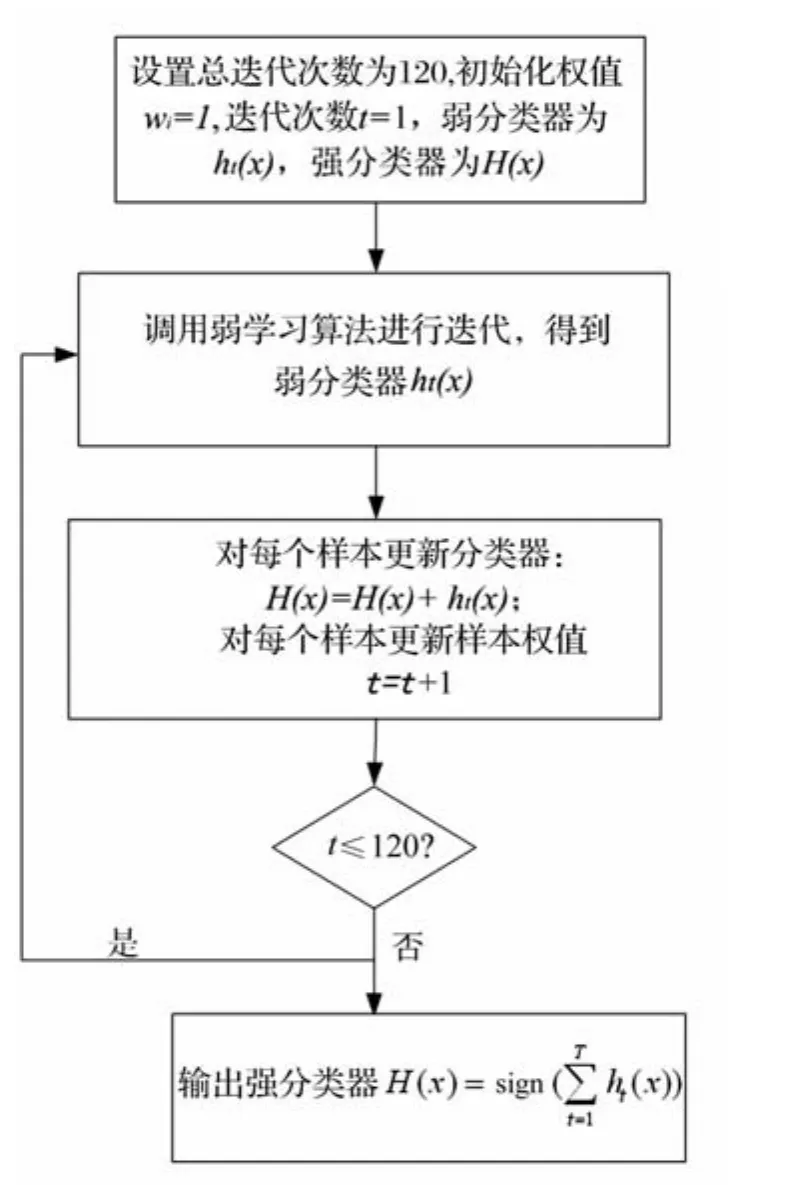
图2 Boosting算法训练检测器

（7）测试检测器:

① 采用步骤（5）计算测试样本的特征值;

② 将特征值代入（6）中进行迭代得到强分类器;

③ 输出包含目标的边界盒;

（8）评估检测器性能:

采用正确率－召回率（Precision-Recall）曲线对检测精度进行全面评估。查全率（recall）用横坐标表示，即检测正确的目标数量与特定类型的所有目标数量的比值;查准率（precision）用纵坐标表示，即检测正确的目标数量与检测目标总数的比值。检测的结果用包含目标的边界盒表示。

算法流程图如图3所示。

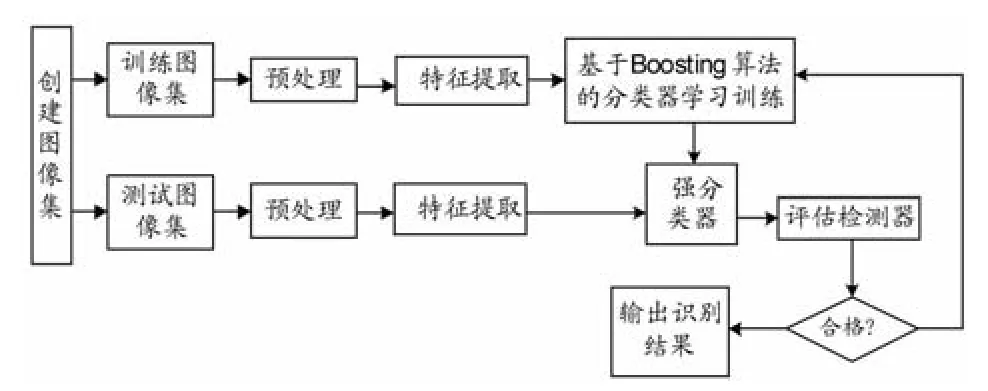
图3 算法流程图

2 实验结果与分析

实验结果如图4所示。

在图4中第一列表示输入真实图像;第二列表示Boosting边界，代表输出分类结果的置信度。y H（x）是Boosting边界［8］，y是样本标签，y= +1表示目标，y=－1表示背景。边界越大，出现目标的可能性也越大;第三列表示阈值处理结果;第四列表示输出包含目标的边界盒。图4（a）（b）表示Boosting对多目

图4 实验结果

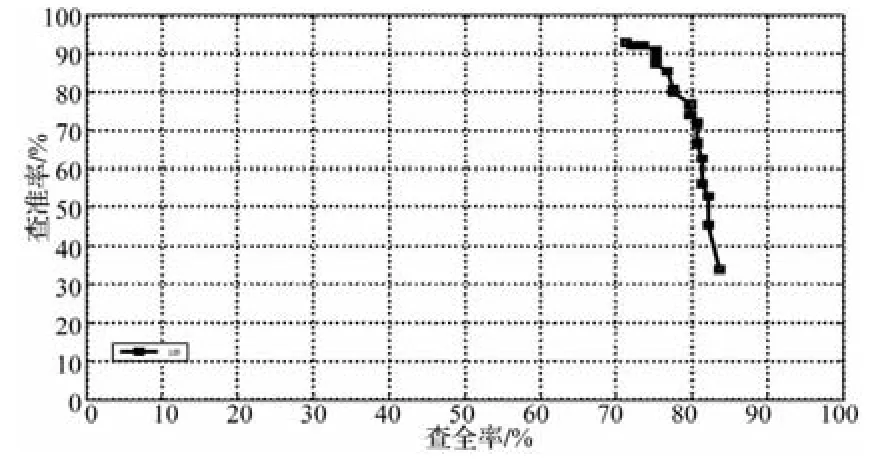
图5 查准率－查全率曲线

标检测的结果，图4（c）（d）（e）表示对单目标的检测结果。从检测结果看:图4（a）（e）的目标被完全正确的检测出来;图4（b）除了car被检测出来，由于建筑物下方边界值太大，被错误检测出来;图4（c）（d）也把car检测出来，由于斑马线的边界值太大，被错误检测出来。Precision-Recall曲线如图5所示。

从图5的查准率－查全率（Precision-Recall）曲线可以看出:开始检测时precision最高，即正确检测到的目标占所有检测到目标的比例最大，recall较低;随着测试图像的增多，检测正确的目标也逐渐增加，因此recall升高，但是错误检测的目标也增多了，所以precision总体呈现下降趋势。最终检测的查全率和查准率分别为83.72%和33.96%。由于car本身的特征很多、噪声的干扰，对实验的结果造成了影响。

3 结束语

Boosting算法收到关注的原因在于它的简单、高效。在实际应用中，我们可以将一个弱学习算法通过Boosting将其提升为强学习算法，使算法精度达到提高。但Boosting也容易受到一些因素干扰如若学习器太弱、训练数据不足、迭代次数不合理、存在噪声等。如何解决这些问题，将是Boosting值得研究的方向。另外，Boosting在语音识别、文本分类、书写体字符识别等实际应用领域也有广泛的前景。

［1］ Valiant L G.A Theory of the Learnable［J］.Communicationsofthe ACM，1984，27（22）:1134－1142.

［2］ Michael Kearns and Leslie G Valiant.Learning Boolean Formulate or Finite Automata is as Hard as Factoring［R］.Technical Report TR －14－ 88 Harvard University Aiken Computation Laboratory，August，1988，28（1）:330－400.

［3］ Schapire R E.The Strength of Weak Learn-ability［J］.Machine Learning，1990，5（2）:197－227.

［4］ Freund Y.Boosting a Weak Learning Algorithm by Majority［J］.Information and Computation，1995，121（2）:256－285.

［5］ Freund Y，Schapire R E .A Decision-Theoretic Generalization of Online Learning and an Application to Boosting［J］.Journal of Computer and System Sciences，1997，55（1）:119 －139.

［6］Friedman J，Hastie T，Tibshirani R.Additive Logistic Regression［R］.A Statistical View of Boosting，1998，28（2）:330－400.

［7］ Friedman J，Hastie T，Tibshirani R.Additive Logistic Regression［R］.A Statistical View of Boosting，2000，28（2）:337－407.

［8］ SCHAPIRE R E.The Boosting Approach to Machine Learning［C］.Proceedings of MSRI Workshop on Non linear Estimation and Classification，New York，2002.