无刷直流电机自适应模糊直接转矩控制研究
2013-09-20陈锟杨晓洪王剑平张果余晓光
陈锟,杨晓洪,王剑平,张果,余晓光
(昆明理工大学信息工程与自动化学院,云南 昆明 650500)
0 引言
无刷直流电机(BLDC)相对于异步电机来说具有功率因数高、结构简单、调速范围宽等优点[1],在高效节能方面应用得比较广泛。但是无刷直流电机存在电磁因素和电流换相引起的转矩脉动[2],同时在传统控制方法下,系统抗扰动能力差,限制了其性能发挥。
直接转矩控制技术[3-4]按照定子磁场来定向,直接利用转矩误差来进行控制,简化了控制环节,同时提高了系统静动态性能。它首先是应用在异步电机控制上,现在针对无刷直流电机结构原理[5]的不同,调整各环节计算模型,合理选择电压矢量,达到减小转矩脉动的目的。
模糊控制技术是一种智能控制技术,它通过经验的办法来建模,对解决一些非线性系统控制问题具有其独特的优势。模糊控制通常结合PID调节技术[6]一起使控制系统兼具了很好的静动态性能。
在由速度环来给定转矩时,传统的办法是通过PI控制器调节速度来获得,这种方法不能很好地跟随动态变化过程,系统的速度和转矩适应性不强。为了获得更加准确的转矩给定,提高系统对扰动适应力,决定使用模糊PID控制器替换之,这样也使得系统对负载变化带来的转矩波动有所抑制。
1 自适应模糊直接转矩控制系统及其转矩模型
如图1所示为系统整体结构图。

图1 无刷直流电机自适应模糊直接转矩控制框图
直接转矩控制通过转矩调节和磁链调节输出,并结合磁链所在位置产生相应的空间电压矢量,控制逆变器开关作用使转矩达到稳定。速度环由模糊自适应PID控制器进行在线调节。
无刷直流电机选择以三相星形连接方式进行分析,忽略定子电阻和交、直轴间的互感,并假设转子为永磁隐极即Ld=Lq(Ld、lg分别为d,q轴电感),则电磁转矩表达式为:

式中:θe为转子电角度;p为电机极对数;isd、isq分别为d,q轴定子电流;Ψrd、Ψrq分别为转子的d,q轴磁链。再进行坐标系变换,得到α-β坐标系下电磁转矩表达式为:
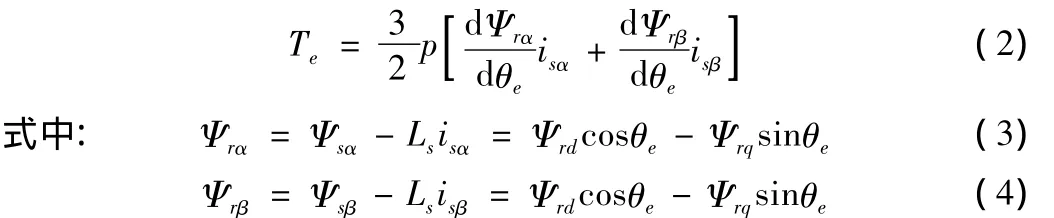
2 直接转矩控制抑制脉动原理
由转矩表达式可知,转矩由定转子磁场相互作用产生,通过控制磁链矢量的旋转即可控制转矩。定子磁链矢量与电压电流的关系为:
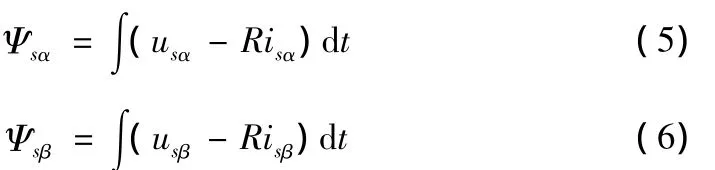
定子磁链的幅值和位置分别为:


图2 空间电压矢量对电动机转矩的调节
根据两两导通方式驱动换相原理,需要用6位二进制数来表示每个电压空间矢量。由此获得六个非零电压矢量 U1(100001),U2(001001),U3(011000),U4(010010),U5(000110),U6(100100)和一个零电压矢量U0(000000),其 位置如图2所示。按照定子磁链Ψs的位置将空间划分为六个扇区,六个非零电压矢量刚好在每个扇区的边界处。在不同的扇区,各电压矢量对定子磁链的作用是不同的。现假设定子磁链旋转至第扇区,如图2。
设t1时刻和t2时刻定转子磁链分别为 Ψs(t1)、Ψr(t1)和Ψs(t2)、Ψr(t2)。当电机t1从时刻运行到t2时刻,定子磁链矢量在空间电压矢量U2(001001)作用下从Ψs(t1)位置转到Ψs(t2)位置,此时转子磁链矢量从Ψr(t1)位置转到Ψr(t2)位置。从图2看到,定子磁链转过角度多于转子磁链转过角度,转矩角变大使得电机转矩增大。如果在这一过程中选择使转矩角变小的电压矢量,电机转矩将减小。相应的电压矢量是根据滞环比较器输出来决定的。
控制中磁链滞环比较器采用三点式输出,转矩滞环比较器采用两点式输出。结合磁链所在的扇区来合理选择电压矢量,这样就可以实现转矩的快速调节,同时也充分利用零电压矢量对转矩的稳定作用。由此得出最优电压矢量选择表如表1。
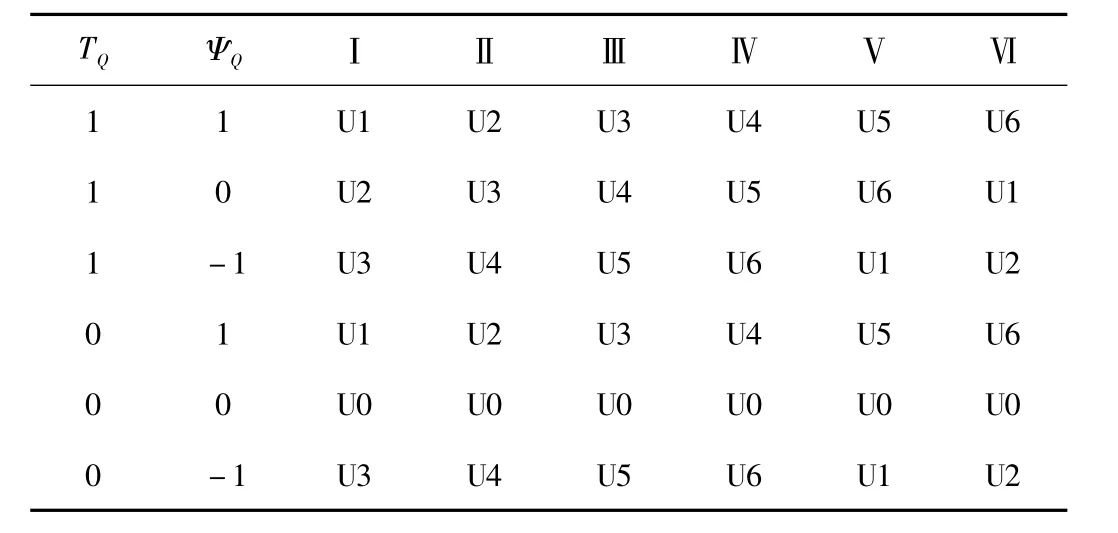
表1 直接转矩控制电压矢量选择表
3 自适应模糊PID控制器设计
利用 MATLAB 的 Fuzzy Logic Toolbox[7],设计和建立一个两输入三输出的模糊控制系统(FIS),转速偏差e和偏差率ec作为模糊控制的两个输入量,输出 PID 参数调整量 ΔK'p、ΔK't、ΔK'd。e和ec的定义分别为:
式中n*(k),n(k)分别为k时刻参考转速和实际转速,T为采样时间。
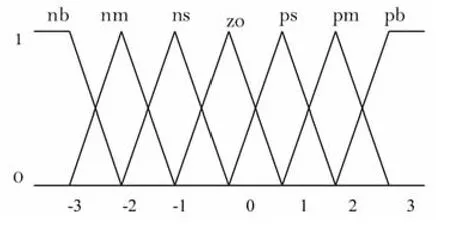
图3 模糊输入输出变量隶属度函数形式
设计使输入输出模糊论域均为{负大(nb)、负中 (nm)、负 小(ns)、零(zo)、正小 (ps)、正 中(pm)、正 大(pb)},采 用Mamdani算法模糊推理,重心法解模糊。模糊输入输出量的基本论域都设为{-3,-2,-1,0,+1,+2,+3}。并且都用三角形隶属函数表示,如图3所示。
通过总结无刷直流电机控制经验,并进行实验比较得到模糊控制规则表如表2、3、4所示。
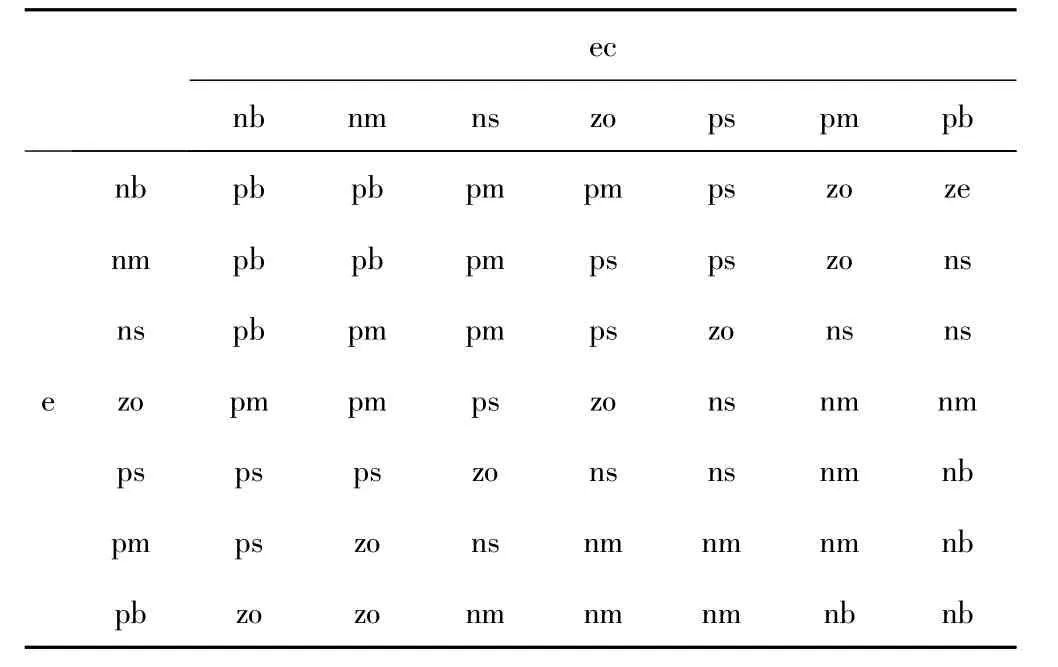
表2 ΔK'p的模糊控制规则表

表3 ΔK't的模糊控制规则表
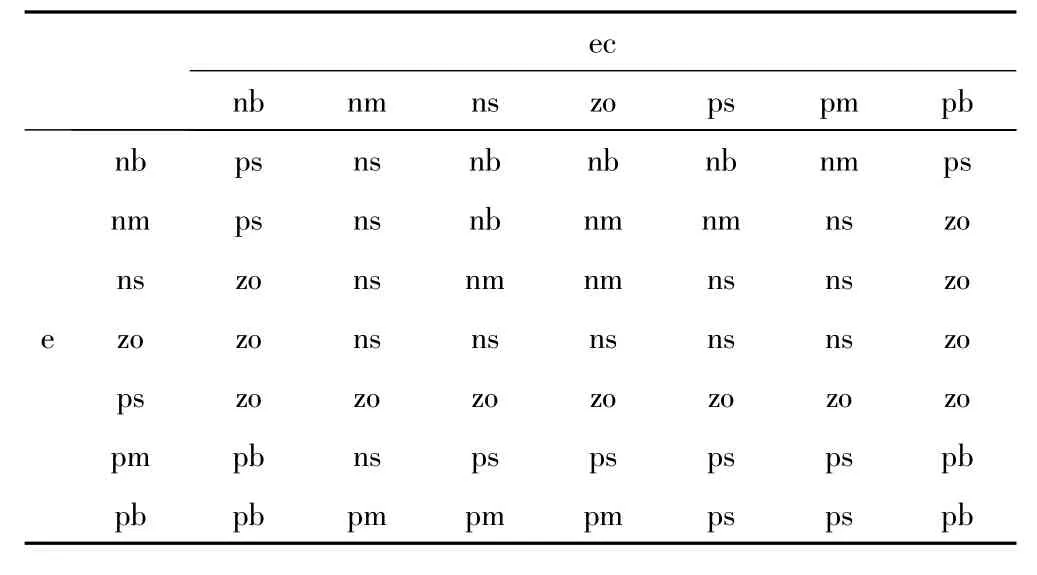
表4 的模糊控制规则表
由表2、3、4可得出49条控制规则的模糊条件语句,模糊条件语句的形式为:If is“pb”and is“nb”then ΔK'pis“pb”.
自适应模糊PID控制器通过调整量实时调节PID参数,获得理想的 Kp、Ki、Kd参数输出。
4 实验结果及仿真波形分析
按照以上几节的理论,在MATLAB动态仿真平台下建模,对控制系统进行仿真。仿真参数设置为:额定电压72 V,定子电阻R=0.8,电感 L=3.2 mH,极对数 p=4,转动惯量 J=8 ×10-5kg·m2。额定转速n=1 000 rpm,电机空载起动,在0.2 s的时候给2 N*m的负载转矩变化,分别进行传统PI调节和模糊PID调节下的直接转矩控制仿真,输出速度和转矩波形进行比较,如图4、5、6、7 所示。
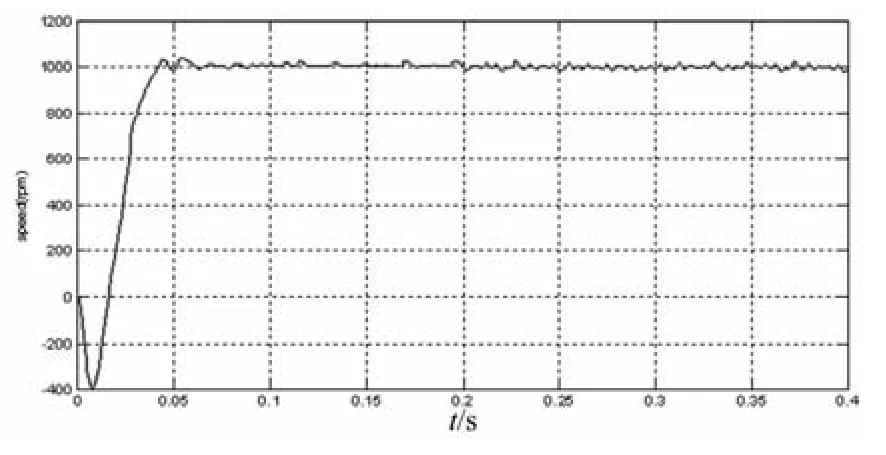
图4 传统PI调节直接转矩控制速度仿真波形
由速度波形比较可知,模糊调节直接转矩控制下的无刷直流电机转速超调变小,负载突变之后的速度也比在传统PI调节直接转矩控制下要更平稳,波动较小。由转矩波形比较可知,在模糊调节作用下,系统对转矩变化的适应能力也更强了。
5 结束语
在无刷直流电机直接转矩控制的基础上,采用模糊控制的
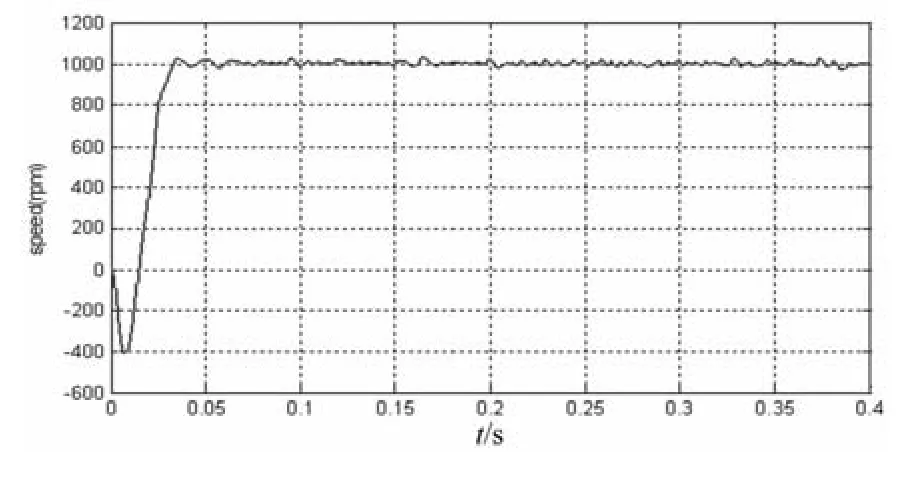
图5 模糊调节直接转矩控制速度仿真波形
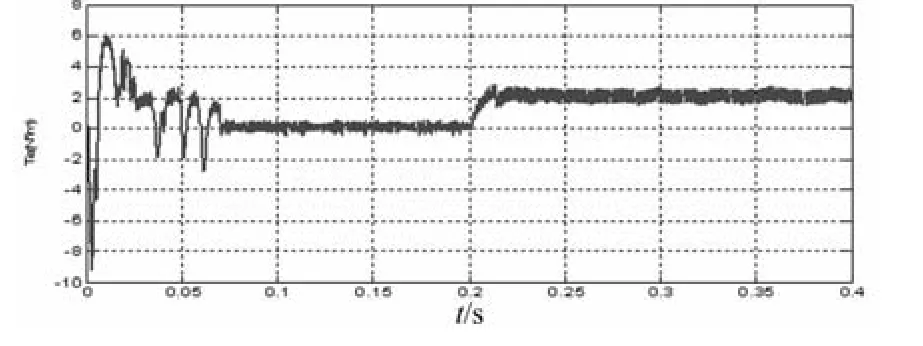
图6 传统PI调节直接转矩控制转矩仿真波形
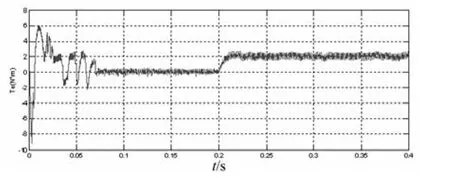
图7 模糊调节直接转矩控制转矩仿真波形
方法调节速度环PID参数,使系统对速度和转矩的变化控制加强。通过仿真实验并进行分析,验证了自适应模糊直接转矩控制方法的有效性。直接转矩控制对转矩输出起到了稳定作用,模糊PID控制较传统的PID控制更灵活,使系统自适应调节能力增强,改善了系统的抗负载扰动能力,保证了系统静态和动态性能。
[1]夏长亮.无刷直流电机控制系统[M].北京:科学出版社,2009:95-102.
[2] Zhu Z.Q.Direct torque control of brushless DC drives with reduced torque ripple[J].IEEE Transactions on Industry Applications,2005,41(2):599-605.
[3] Hoang L H,Robert P,Feuillet R.Minimization of torque ripple in brushless DC motordrivers[J].IEEE Transactionson Industry Application,1986,22(4):748 -755.
[4]刘兴艳.基于DSP的无刷直流电机的控制研究[D].河南:河南理工大学.2010.
[5]夏长亮,张茂华,王迎发,等.永磁无刷直流电机直接转矩控制[J].2008,28(6):104-109.
[6]孙施良,王阳明.模糊控制系统的MATLAB仿真过程[J].机械与电子,2005,20(1):14 -16.
[7]薛定宇.基于MATLAB/Simulink的系统仿真技术与应用[M].北京:清华大学出版社,2005:85-94.
[8]阮毅,陈伯时.电力拖动自动控制系统:运动控制系统[M].4版.北京:机械工业出版社,2011:191-195.
