基于Gabor小波的特征提取技术应用

刘传领

(商丘师范学院计算机与信息技术学院，河南商丘476000)

1 .引言

人脸识别的关键是在特征提取阶段提取特征点，并且特征点要具有可分类特性。人脸特征可分为两类，即直观特征和代数特征，截至目前，学者们已经提出了很多的人脸特征提取算法，这些大致可分为两类：经典线性算法和基于流行学习的算法。PCA、LDA、ICA、MMC等方法被称为经典线性算法，拉普拉斯特征映射、局部保持性的投影方法、等容映射方法、局部线性嵌入方法和边界分析法等被称为基于流行学习的算法。二维图像是人脸识别中表达人脸最常采用的图像，原始特征和基于原始特征的变换特征是组成人脸图像特征的两个主要组成部分，基于原始特征的变换特征是采用某种变换核在原始图像基础上进行变换得到的，是一种全新的描述，是在一个空间针对原始图像进行的。目前我们经常用到的变换特征有基于频率的特征、K－L变换特征、直方图特征等。基于频率的特征可细分为傅立叶变换特征、小波特征，小波特征也可以分成很多种类，如Harr特征、Gabor特征等。

2 .Gabor小波的特征提取技术

2.1 Gabor小波技术

任意∀f∈L2(IR)的傅里叶变换为(w)=，由公式可以看出傅里叶变换可以很好地提取信号f(t)的整体频率信息。但观测信号在局部特性的情况下效果很差。［1］

1946年Dennis Gabor提出傅里叶变换，采取时间局部化的最优窗——Gaussian函数。

其一维小波变换如下：

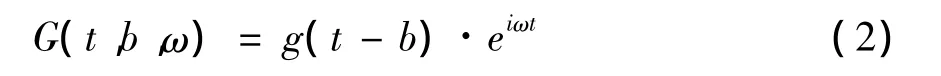
其中g(t)为高斯函数。因此对于∀a＞0，∀f∈L2(IR)的小波变换如下：

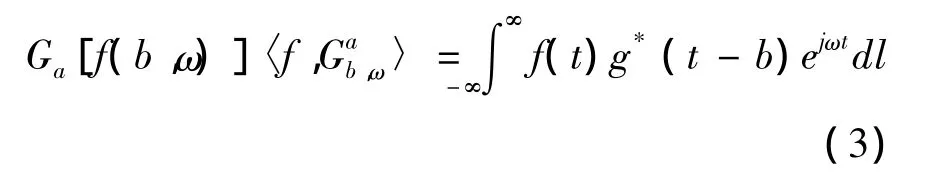
其中g*(t－b)表示函数g(t－b)的共轭。因此可以看出Gabor满足Parseval恒等式。

Daugman将Gabor扩展成二维形式

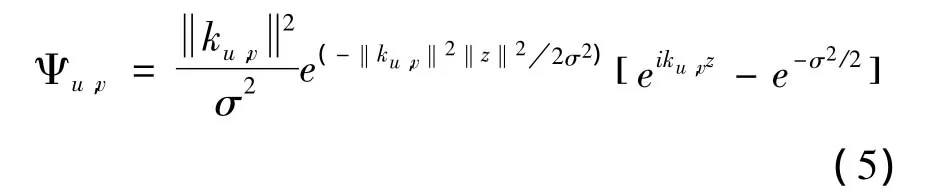
式中，Gabor小波核的方向和尺度分别是用u，v进行表示的，图像中的像素点是用z=(x，y)进行表示的，相应值的欧氏范数是用 ·进行表示的。高斯窗口的宽度大小是用ku，v进行控制的，用式(6)来定义震荡部分的方向及波长大小

式中，滤波器的采样频率用kv=kmaxfv表示。最大采样频率用kmax表示，间隔因子用f进行表示，作用为限制频率中和函数。滤波器的方向选择性用φu=πu8进行表示。高斯窗口的宽度大小与波长大小之比是由参数σ决定的，它与滤波器的带宽的关系用式(7)进行表示：

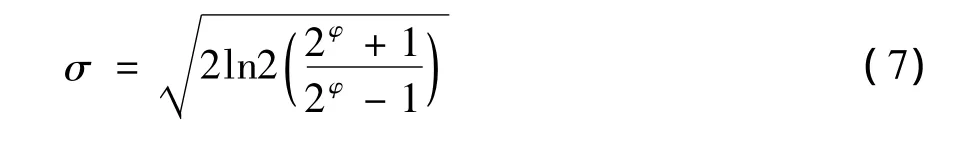
其中，包含倍频程的半峰带宽用φ进行表示。他们之间的关系如下：φ=0.5倍频，σ≈2π;φ=1倍频程，σ≈π;φ=1.5 倍频，σ≈2.5。

从式(5)可以看出中Gabor小波核函数具有自相似的特点。通过调节u及v，即改变方向参数尺度参数，这样它们就可以由母函数统一生成，对滤波器进行适当的尺度变换及旋转。震荡部分是Gabor核的重要组成部分，补偿直流分量是由第二部分完成的。参数σ的主要作用是决定高斯窗口宽度大小与波长大小之比的，直流分量在σ的值较大时，是可以忽略的。

通过Gabor函数与图像I的卷积可以求出图像I(x，y)的Gabor滤波z0(x0，y0)，如果是图像中一个像素点，点z0附近区域的图像特征可以通过Gabor小波变换的卷积进行描述，其卷积计算过程用公式表示为：

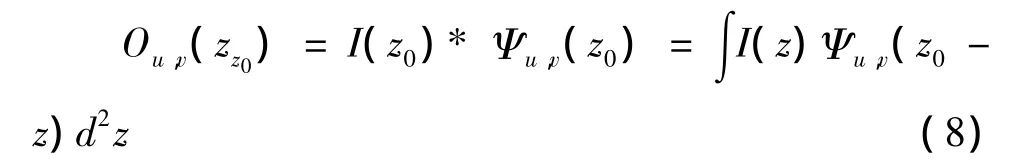
其中，卷积用* 进行表示，点z0处的卷积值大小是用Ou，v(z0)进行表示的。为了获得图像特征，特别是在多方向、多尺度的局部显著性特征，我们通常用一组Gabor核函数表示，它们各自具有不同的u及v(u=0，…，U－1，v=0，…，V－1)，即方向参数和尺度参数。所以，集合S={Ou，v(z)：u∈ {0，…，U－1}v∈{0，…，V－1}}形成了图像I的Gabor小波特征表示。

对于Gabor的参数的选择依然是一个开放性的问题。通常情况下，我们取V=5(v=0，1，…，4)，U

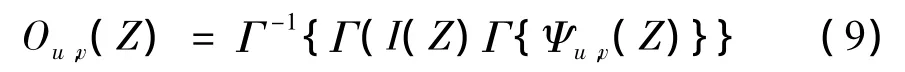
Gabor特征的维数过大增加了计算量和运算时间，为了减少Gabor特征的维数，Liu和 Wechsler提出下采样的技术理论，这种理论的核心思想是表示区域特征时，可以通过在小的局部区域计算 Gabor小波幅值的均值的方法。如果把计算得到的下采样的特征按顺序级联起来，这样就形成了人脸的特征向量集合，然后将特征向量通过投影映射到更低维的子空间，这个过程可以通过对线性判别分析法进行改进来计算。

2.2 特征提取原理

由上论述可知一幅128*128的人脸图像经过Gabor变换之后变为128*128*40，数据量显著增大。针对该问题有的学者提出通过下采样来把数据量降下来，即对于一个样值序列间隔几个样值取样一次，这样得到新序列就是原序列。［2］假设每一对(u，v)取64个数据点，每幅图像共产生64*40=2560个数据点。因此，数据量过大不利于直接进行识别，需要对图像降维。降维的算法较多，本文针对FLDA(Fisher Linear Discriminant Analysis)进行。

设X=(x1，x2，L，xN)为样本数据集，其中xi∈RD，i=1，2，L，N。cj∈ {1，2，L，Nc}为样本xi的类别标签，式中样本数据集类别数为Nc，ni为第i类的样本的总数。P为LDA寻求最优的映射变换矩阵，将iD空间的数据通过映射投影到一个相对低维的特征空间id(d＜＜D)中。映射函数［3］可表示为：

i类样本均值计算如下：

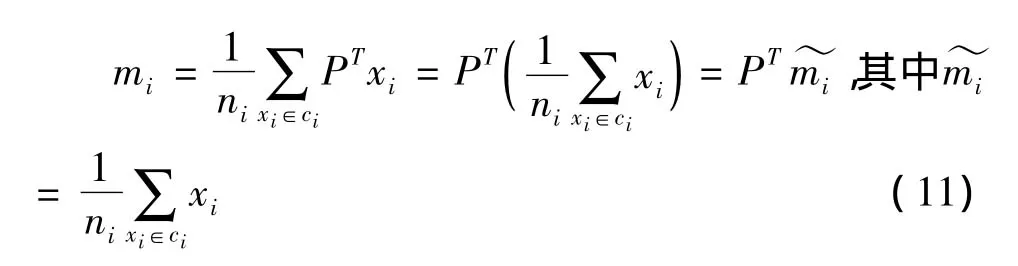
总体样本均值：

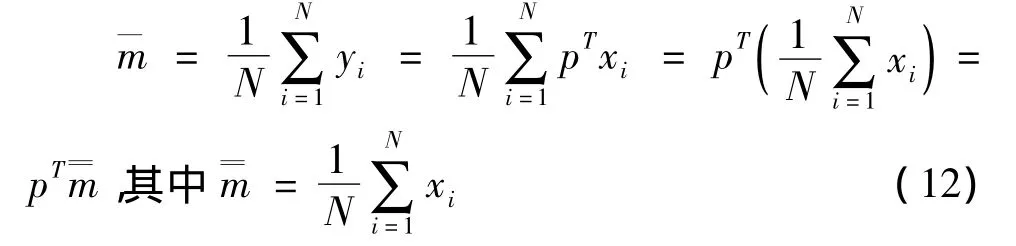
LDA的目标函数如下：

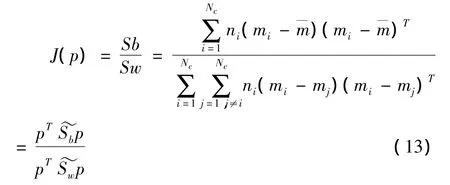
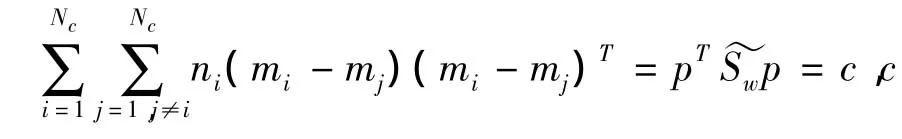
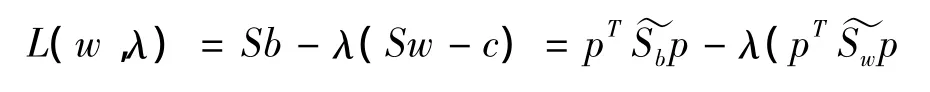
式(14)对p求微分可得：

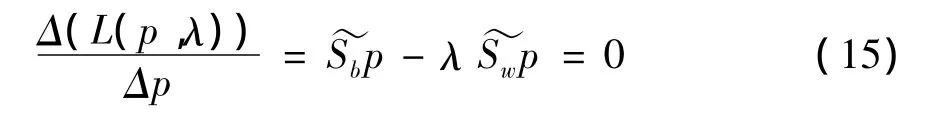
即：

由于和是半正定并且对称的，当满秩时，式(16)的特征值和特征向量的值可通过()－1进行计算。

3 .实验步骤

利用LDA计算投影矩阵的步骤如下：

(1)利用Gabor提取每幅人脸图像的特征形成x;

(2)x是输入的训练样本，利用式(13)和(14)计算分别得到和，其中是类间离散度矩阵是类内离散度矩阵;

(3)式(18)可用来计算特征值与特征值对应的特征向量;

(4)可以计算得到最大的d个特征值，用其对应的特征向量组成投影矩阵P。

4 .结束语

本文以代数特征为研究重点，这些特征是图像中具有最大分类特征、可分类特性非常好的像素点，这个环节是其中非常重要的一个环节，也是人脸识别准确率的一个关键。人脸图像包含非常多的冗余特征和信息，是高度冗余的图像，去掉冗余特征后对最终的识别效果基本没有影响。

［1］Mallat S.信号处理的小波导引［M］.2版.杨力华，等译.北京：机械工业出版社，2002.

［2］张立，赵福才，张玉.基于小波包分解的图像特征提取及应用［J］.舰船电子对抗，2007，30(4)：92 －85.

［3］成礼智，王红霞，罗永.小波的理论与应用［M］.北京：科学出版社，2004.