求解在弱条件下带不可微项的Broyden方法的收敛性

杜玉琴，孙超

(1.中国青年政治学院经济系，北京100089;2.中国传媒大学理学院，北京100024)

1 预备知识

本文在文献基础上讨论了求解非线性方程组

的Broyden方法在弱条件下的收敛性。

设f:D⊆RN→RN在凸区域D上二次可微，x0∈D记

我们有

Df(x0)-1存在，λ，β，γ 为给定正数，f满足

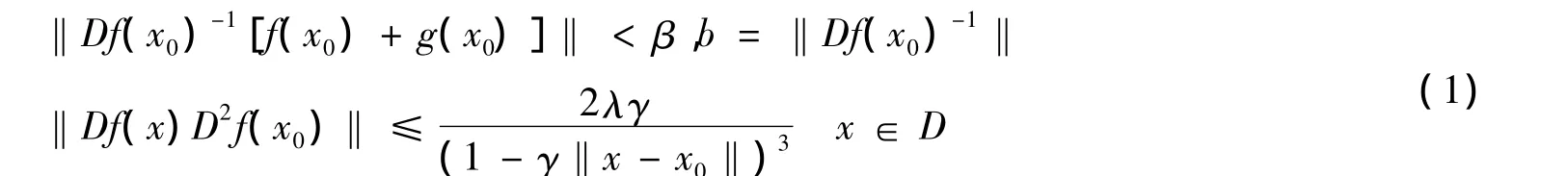
单调递增收敛于t*。

证明 依h(t)的定义有

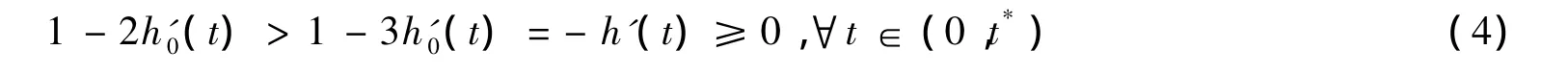
即 φ(t)在［0，t*］上有意义。因

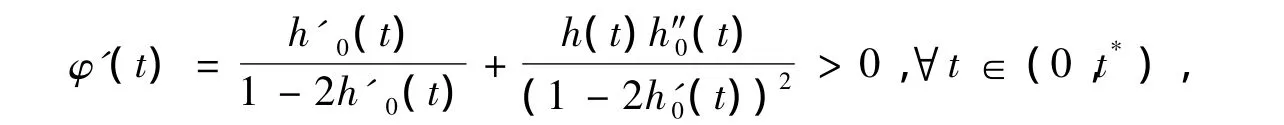
易知 φ(t)在［0，t*］上单调递增，若0 ＜ tk＜ t*，则

用归纳法得由(3)式产生的迭代{tk}是一个单调递增有界序列，令式中令 k→∞，得 φ(t-)=0，即 t-=t*，证毕。

引入记号

我们有

引理3 设0＜R ＜S＜T≤t＊＊，u，v，w∈D 满足

如果f满足(5)，则

2 主要结论

定理1 由于

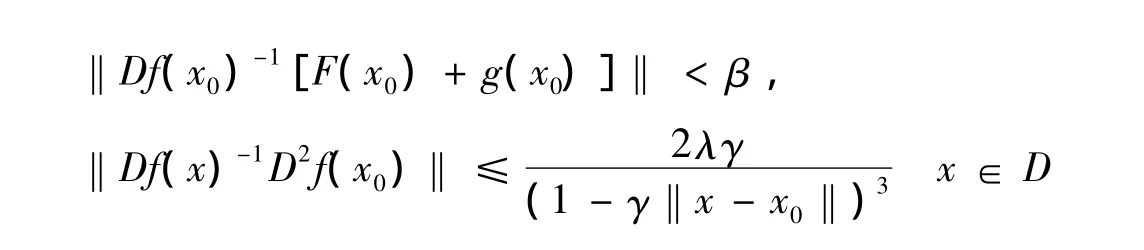
的两个零点。

证明 首先证明对于所有k，恒成立

用数学归纳法，依定理假设当k=0时(7)成立，先假设当时1≤k≤n，成立，有

当k=n+1时，由{Bk}的定义，易知

利用引理2，引理3及归纳法可证

又根据迭代(3)式

于是，根据φ'(t)的单调递增性，

另一方面

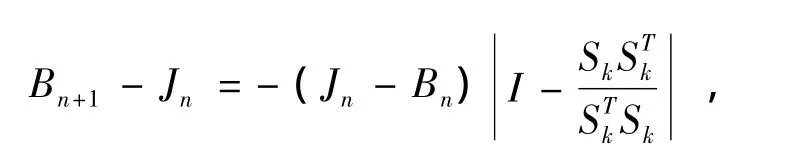
根据(8)及引理3，

由Banach定理

从而

这说明，当k=n+1时，(7)式仍成立。依归纳法得证。由引理1知，{xn}是一个柯西序列，设其极限为x*，(9)式中令 n→∞，得

依(7)式，可推得

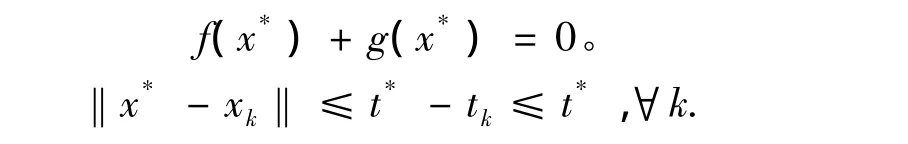
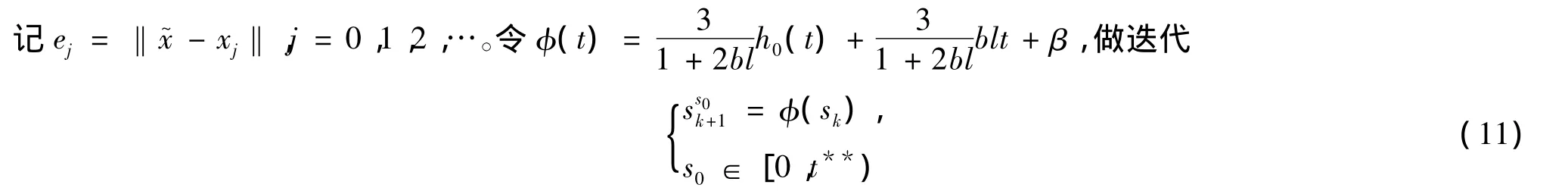
则由φ(t)在区间［0，t＊＊)中的单调及向下的凸性质，用归纳法可证:

仿照(9)式可得

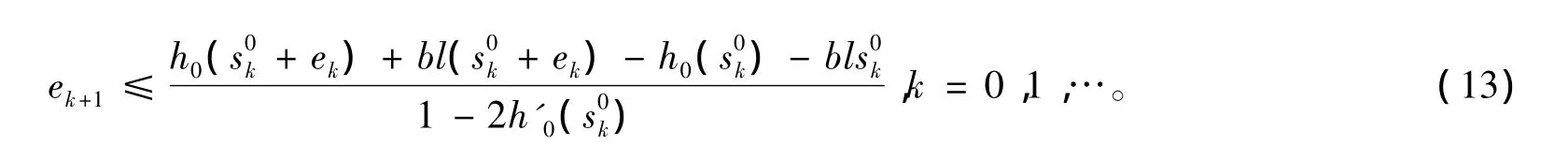
进一步有

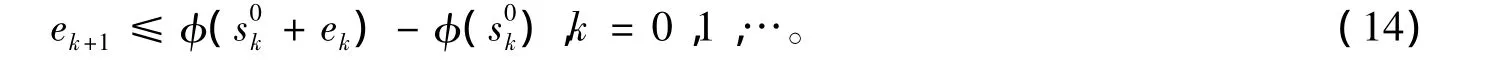
事实上，令w＞0，则函数φw(t)=wh0(t)+wblt-t+β的较小零点随w的增加而增加，w最多增加到，使得φw-(t)恰有唯一零点，此时φw-(t)的驻点(t)也是φw-(t)的零点，即满足φw-)=0及

若取

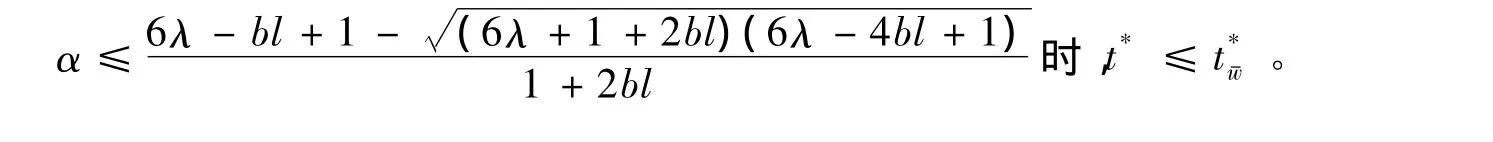
于是

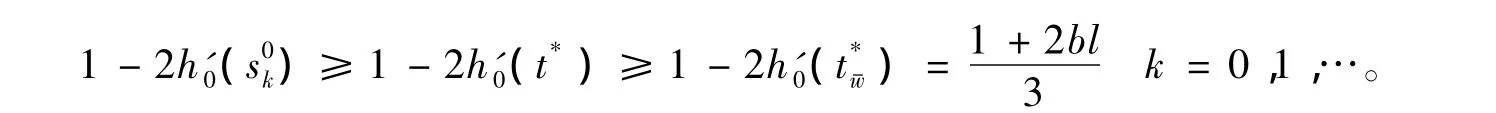
归纳即得(14)式对一切k≥0恒成立，改写(14)为如下形式

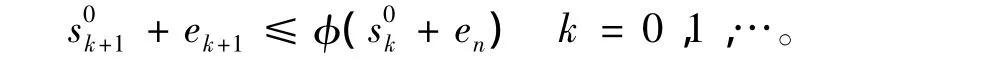
［1］王兴华，韩丹夫.弱条件下的判据和Newton法［J］.计算数学，1997，2(1):103-111.

［2］王兴华，韩丹夫，孙方裕.若干变形Newton迭代的点估计［J］.计算数学，1990，12(2):145-156.

［3］Xiaojun Chen，Tetsuro Yamamoto.Newton-like methods for solving underdetermined nonlinear equations with nondifferentiable terms［J］.Journal of Computational and Applied Mathematics，1994，55:311-324.

［4］Ioannis K Argyros.OntheConergence of a certain class of iterative procedures，under relaxed conditions with applications［J］.Journal of computational and applied mathematics，1998，8(1):13-21.

［5］Tetsuro yamamoto.Historical developments inconvergence analysis for Newton^s and Newton-like methods［J］.Journal of Computational and Applied Mathmatics，2000，124:1-21.

［6］Andreas Rieder.On convergence rates of inexact Newton regularizationsNumer［J］.Math，2001，88:347-365.

［7］Qinian jin.A Discrete Scheme of Landweber Iteration for Solving Nonliear Ill-Posed Problems［J］.Journal of Mathmatical Analysis and Application，2001，76:187-203.

［8］JM Gutierrez，M A Hernandez.An acceleration of Newton’s method:Super-halley method［J］.Applied Mathmatics and Computation，2001，117:223-239.

［9］Asen L Dontchev，Houduo Qi，liqun Qi.Convergence of Newton smethod for convex best interpolation［J］.Numer Math，2001，87:435-456.