初中数学几何图形语言的训练策略

袁建平

（苏州市吴江区八坼中学，江苏 苏州 215222）

二、几何图形语言训练的要求与方法

（一）画（作）图要规范

1.合理地使用画图工具

在几何教学中，对不同知识点的画图，要求虽有差异，但都必须使用三角尺、直尺、圆规、量角器等画图工具来完成，不可以随意降低几何画图的要求。新课程重视学生动手画图能力的培养，教师要引导学生不断实践画图并总结精确作图的方法与规律，要使学生认识并体会到，徒手画图或工具使用不当，不仅有失图形的准确和美观，还会诱发解题的错误思路。所以，教师要培养学生养成合理使用画图工具，用画图工具精确作图的良好习惯。

2.精确标记对应字母和数字

当所画图形需要标记字母时，要注意区别使用大小写字母。例如，在画线段的和与差时，题目中所给出的线段一般情况下用小写英文字母标注，而画出线段的和与差则可用大写英文字母标注。又如在区别不同的角时，可以在角的顶端画一条弧线，用数字1、2等进行标记。标记的字母和数字要准确，且标记的对应位置要适当，图形和相对应的叙述文字要保持一致。

3.明确区分实线和虚线

梨花不知自己为何没有离开大寨河，没有离他而去，她只是沿着河北岸走；或许在她心里是想听方竹要问的那句话的。方竹在河南岸追她，他问：“小妹，你为什么要答应？”梨花突然站住了，隔岸冷笑道：“姐夫，你不是都亲过我姐了吗？”方竹反问道：“我亲过她什么了？那次她绣花边刺破了手指，突然伸到我嘴里，你不是看到的吗？”梨花想起来了，但现在说这些还有什么意思呢？梨花只是走，埋着头急急地走。不知不觉中，他们走到了八字桥的地方。方竹过了桥，追上梨花。他说：“小妹，不管你信不信？我心里……”梨花没有让他再说下去。

画图过程中，依据题目要求画的线要画成实线，而根据解题需要添加上的线则画成虚线，要区别对待。例如，在画钝角三角形外部的高时，可先用虚线画出底边的延长线，再用实线画出对应顶点到这条边上的高。又如，用平行线间距离的意义解决问题时，所画的平行线间的距离线要用虚线。

4.画图要尽量接近问题的实际

数学画图与机械制图不同，多带有示意的性质。教学时教师所画出的图应做到基本符合问题的实际，这对帮助学生思考及论证是非常有益的。

（二）特殊图形与一般图形之间不能互相替代

有的学生为了图形的美观，画图时往往将一般的图形画成特殊的图形，比如将直角三角形画成等腰直角三角形，将矩形画成正方形，将一般的三角形画成等腰三角形等，这样会导致学生把特殊图形的特殊性质误认为是一般图形的性质，由于表达的几何图形语言有误，其所得出结论也是有误的。

进行几何图形语言训练时，需要画一些非标准位置的图形。例如画一个等腰三角形，不要总把它的底边放在水平位置，顶点放在水平线的上方。如这样的一个问题：将两个全等的直角三角形拼成一个规则图形，有几种不同的情形？由于学生不习惯画出不同位置的直角三角形，最后在得出的结论中往往会漏掉了平行四边形的情形。

（三）加强三种数学语言的互译，灵活运用几何知识

学习几何基本概念，要文字语言与图形语言相结合。几何概念和图形是紧密联系的，几何图形比文字表述的概念，更容易印入脑际。为了加深对几何基本概念的理解，要学会画出相应的图形。例如在学习邻补角的概念时，准确地画出几何图形，更容易体现出互为邻补角的两个角的位置关系和角度关系，学生也容易把邻补角与补角进行比较、区别清楚。又如学习三线八角图时，三种位置关系的角分别可以用一个简单的图形来显示，这个抽象概括的过程由学生讨论得出后，文字语言与图形语言相结合，概念就深刻地印在学生的脑海中了。

学习几何的推理、说理，要文字语言、符号语言和图形语言相结合。学生在初学几何的推理、说理时，主要对推理论述的格式、各种性质及其判定方法等方面的理解和运用比较困难。为解决这个难题，教师要指导学生将所学的有关几何概念、性质、判定方法的文字语言、符号语言和图形语言结合起来，同时训练学生写出分段式的说理过程。如：学习角平分线的意义及其应用，垂直的意义、平角的意义、邻补角的意义，对顶角相等的性质、平行线的性质、判定等，可将关于这些相关概念的文字语言叙述和符号语言、几何图形语言对应记忆。在学生熟悉了基本的几何图形而且能够熟练运用每个概念、性质和判定方法后，再将稍微复杂一些的几何推理题，用几个简单说理组合的方式进行解析，在此基础上，逐步提高难度，为学生学会几何推理、说理扫清障碍，提高他们运用几何图形语言解题的能力。

熟练地对文字、符号与几何图形这三种语言形态进行转化使用，这是中学数学教学进行基础能力训练的目标之一，也是一个难点。正是由于数学语言表达的系统及其方式与初中学生通常的语言习惯不一致，使得较大一部分学生不能自觉地将自然语言形态切换到数学语言的表达形式上，对数学语言理解上的困难就成了学好数学的绊脚石。因此，不少数学问题的解题过程，实质上就是加强不同数学语言形态互译能力的训练。

例如，在初一年级学习“等腰三角形三线合一”的性质时，学生起初对该性质用文字语言所阐述的意义理解不清，在推理过程中总是出现“张冠李戴”的现象。从本质上看，这种现象反映出学生对三种语言的互译能力上存在欠缺。

该性质表述的自然语言形态，可为以下三种形式：

（1）在等腰三角形中，顶角的平分线垂直平分底边；

（2）在等腰三角形中，底边上的中线也是底边上的高、顶角的平分线；

（3）在等腰三角形中，底边上的高平分底边和顶角。

与其对应的三种符号语言，可分别列式如下：

（1）在△ABC中，AB＝AC。如果∠BAD＝∠CAD，则有 AD⊥BC，BD＝CD；

（2） 在△ABC 中，AB＝AC。如果 BD＝CD，则有∠BAD＝∠CAD，则有 AD⊥BC；

（3）在△ABC中，AB＝AC。如果AD⊥BC，则有BD＝CD，∠BAD＝∠CAD。

与其相对应的三种几何图形语言，可分别画图如下：图 1、图 2、图 3。

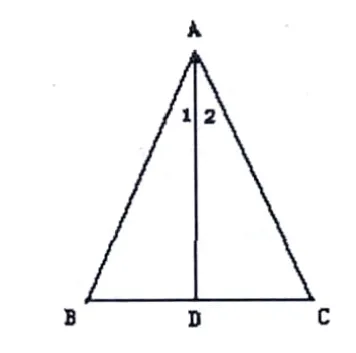
图1

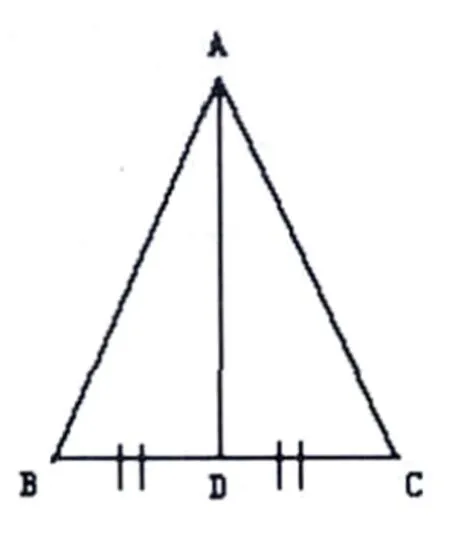
图2

图3

三、几何图形语言训练中必须遵行的原则

在几何图形语言训练中，教师要掌握好以下原则：

循序渐进原则。要遵循新课程标准，依据新教材分阶段的教学目标，按次序、有步骤地在不同阶段用不同的要求进行训练，以求逐渐提高学生的能力。

互动性原则。采用现代化的教学手段和方法，加强师生、生生之间的互动交流，以求提高训练的效率。

趣味性原则。让学生在几何图形训练中，感受到数学图形的美，从而乐于学习数学，善于学习数学。

数学几何图形语言虽不像符号语言那么抽象，但掌握几何图形语言也不是一个简单的过程，只有训练有素的学习者才能运用自如。通过训练，学生既能够灵活运用几何图形语言，反过来也会促进他们对文字语言和符号语言的理解，提高三种数学语言互译的能力。

[1]巨周凯.初中数学空间与图形教学的难点与有效的教学策略[J].数学学习与研究，2012（6）.

[2]谢汉元.浅谈平面几何语言的教学[J].中学数学，1992（7）.

[3]李秀锦.在平面几何语言训练中培养学生素质[J].基础教育研究，2001（1）.