助飞鱼雷雷箭分离过程多体动力学建模与仿真

白照高1, 王锋辉2, 温 震2



助飞鱼雷雷箭分离过程多体动力学建模与仿真

白照高, 王锋辉, 温 震

(1. 海军装备部驻西安地区军事代表局, 陕西西安, 710054; 2. 中国船舶重工集团公司第705研究所, 陕西西安, 710075)

通过分析助飞鱼雷运载体-分离舱组成的多刚体系统的结构与受力情况, 建立了组合体运动的拉格朗日方程, 并采用4阶Runge-Kutta法对给定初始条件下组合体的运动状态进行了仿真计算, 通过和飞行试验数据对比, 验证了多体动力学模型的正确性, 为分析雷箭分离过程的安全性提供了理论支撑。

火箭助飞鱼雷; 多体动力学模型; 拉格朗日方程

0 引言

助飞鱼雷一般由运载体和战斗载荷(鱼雷)两部分组成, 鱼雷安装在运载体前端, 由分离舱将鱼雷和运载体固定连接, 见图1。当助飞鱼雷发射后飞行到预定的雷箭分离点时, 控制系统发出雷箭分离指令, 2片分离舱壳体分别朝2个相反方向迅速打开一定角度, 解除对鱼雷的约束, 鱼雷以原速度继续向前飞行, 而运载体和分离舱壳体组成的多刚体系统, 因受较大气动阻力作用而相对于鱼雷向后运动, 实现鱼雷与运载体的分离。运载体与2片分离舱壳体组成的多刚体系统(简称组合体)在分离瞬间的运动状态比较复杂, 该系统内3个主要部分的运动相互影响, 若组合体与鱼雷雷体运动发生干涉, 则会造成分离过程碰撞, 影响鱼雷作战使命的完成, 因而分析运载体与2片分离舱壳体组成的多刚体系统的运动对研究雷箭分离过程安全性至关重要。

多体动力学建模常用的方法包括Schiehlen法、Wittenburg法、Kane法和Largrange法等。Schiehlen法是牛顿-欧拉法在多刚体系统中的推广, 需要求解系统内部的约束力。Kane法和Wittenburg法适用于由大量刚体组成的系统。由于雷箭分离过程中更关注运载体与分离舱壳体的运动参数, 而非其内部约束力, 因而本文采用Largrange法, 运用分析力学理论建立组合体系统的多体动力学模型。

1 运载体-分离舱组合体动力学分析

按照图1所示的雷箭分离示意图, 为了方便对组合体的动力学分析, 将运载体-分离舱组合体的结构形式简化为如图2所示。

由于分离过程在很短时间内完成, 可假定组合体的运动主要在纵向平面内, 因而可以采用简化的纵向平面内的系统运动模型。为不失一般性, 按照2片分离舱壳体分别朝上、下方向打开, 这样运载体-分离舱组合体的受力如图3所示。

2 组合体运动的多体动力学模型

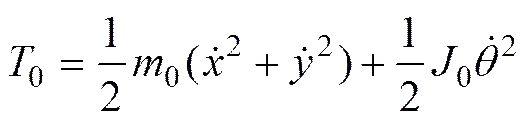
分离舱上壳体的动能为

+

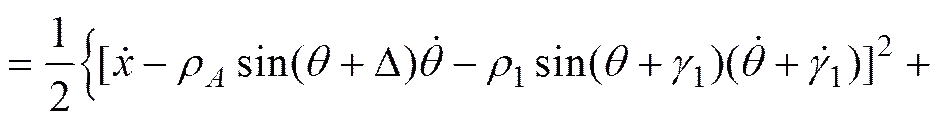
(2)

分离舱下壳体的动能为

+

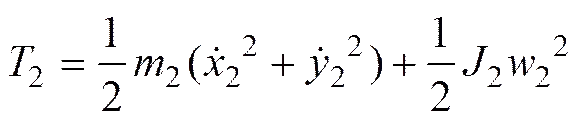
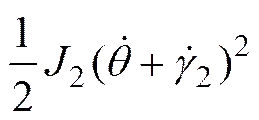
因此组合体系统总动能为

+

+

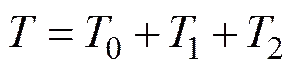
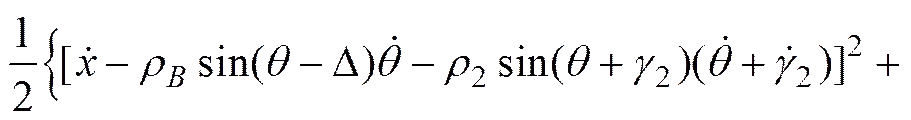
(4)

定义组合体系统的广义坐标为

则相应的广义速度为

(6)

相应的广义力为

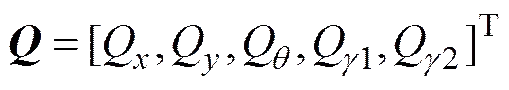
由虚位移原理可解得

(8)

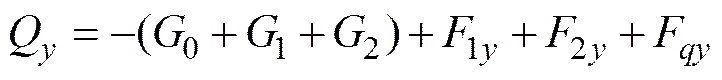
(10)

(11)

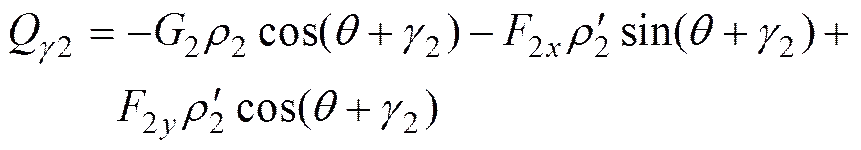
这样, 运载体与分离舱上、下壳体组成的多刚体系统运动的拉格朗日方程为

(13)

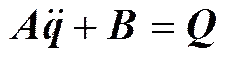
式中:为5×5矩阵;为5×1矩阵的系数矩阵, 其表达式比较复杂, 在此不再赘述。

同时可以很容易建立组合体的运动学方程组

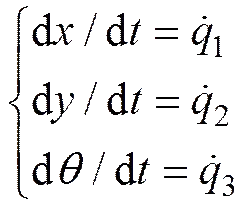
(16)

这样, 由式(14)~式(16)就组成了运载体-分离舱组合体在分离过程中完备的动力学运动学模型; 分离舱壳体和运载体所受气动力采用模型产品风动吹风试验数据计算。只要给定初始分离条件, 就可以完全确定运载体与2片分离舱壳体组成的多体系统的运动状态参量。通过和鱼雷运动状态参数比较, 可以分析雷箭分离过程是否发生碰撞, 分离过程是否安全。

3 仿真结果与分析

按照以上数学模型, 对运载体和分离舱的运动状态进行仿真计算, 计算的初始条件为雷箭分离时刻, 即,,,,,,,,,,。

通过仿真计算, 运载体质心在纵向平面内的相对运动弹道如图4所示, 运载体姿态角的变化如图5所示。

由图3～图6中的结果可知, 在雷箭分离后, 运载体质心的相对运动弹道、姿态角变化以及上下分离舱张开过程和飞行试验的结果非常接近, 表明建立的数学模型正确, 可以用来对雷箭分离过程进行分析。

4 结束语

本文通过分析助飞鱼雷运载体-分离舱组成的多刚体系统的结构与受力情况, 建立了组合体运动的拉格朗日方程, 并采用4阶Runge-Kutta法对给定初始条件下组合体的运动状态进行了仿真计算, 通过和飞行试验数据对比, 验证了模型的正确性, 为分析雷箭分离过程的安全性提供理论参考。

[1] 钟伟国曹志荣. 反潜战技术手册[M]. 北京: 中国舰船信息中心, 2000.

[2] 袁士杰, 吕哲勤. 多刚体系统动力学[M]. 北京: 北京理工大学出版社, 1992: 35-55.

[3] 张劲夫, 秦卫阳. 高等动力学[M]. 北京: 科学出版社, 2004: 135-142.

[4] 刘延柱. 高等动力学[M]. 北京: 高等教育出版社, 2001: 179-204.

[5] 何民, 唐硕, 许志. 基于凯恩方法的箭伞系统动力学建模与分析[J]. 飞行力学, 2010, 28(5): 39-42.He Min, Tang Shuo, Xu Zhi. Modeling and Analysis of Rocket-parachute System Dynamics Based on Kane Method [J]. Flight Dynamics, 2010, 28(5): 39-42.

[6] 张裕兵, 周洲. 机载导弹发射的多体动力学模型[J]. 科学技术与工程, 2010, 10(14): 3389-3393.Zhang Yu-bing, Zhou Zhou. The Multibody Model of Airborne Missile Launching[J]. Science Technology and Engineering, 2010, 10(14): 3389-3393.

(责任编辑: 陈 曦)

Modeling and Simulation of Multi-body Dynamic for Rocket-Assisted Torpedo Separation

BAI Zhao-gao, WANG Feng-hui, WEN Zhen

(1. Xi′an Representative Bureau, Naval Armament Department, Xi′an 710054, China; 2. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China)

This paper analyzes the structure and force of the multi-rigid-body system composed of vehicle and separating cabin, establishes a Lagrange equation of multi-body dynamic model, and then simulates the motion state of the combined system in a given initial condition by fourth-order Runge-Kutta method. The multi-body dynamic models are verified by comparing the simulation results with the test ones. This study may provide a basis for safety analysis of the separation process of rocket-assisted torpedo.

rocket-assisted torpedo; multi-body dynamic model; Lagrange equation

TJ631.8

A

1673-1948(2013)03-0171-04

2012-12-18;

2013-03-15.

白照高(1966-), 男, 高级工程师, 主要研究领域为鱼雷工程.