一种基于D-S证据理论的Bayes可靠性评定方法
2013-09-19赵仿泽
赵仿泽
一种基于D-S证据理论的Bayes可靠性评定方法
赵仿泽
(西北工业大学航海学院, 陕西西安, 710072)
如何合理利用多源先验信息, 是小子样Bayes理论方法应用中亟待解决的一个问题。目前, 多源信息融合还没有统一的准则, 融合理论方法的不同会使得融合结果有所差异。为了解决上述问题, 基于证据推理理论, 提出了一种多源信息先验分布融合方法, 将通过各种融合准则获得的先验分布进行再融合, 得到了一种合理的综合先验分布, 最后建立了基于证据理论的Bayes可靠性评定模型。仿真结果表明, 该融合方法是合理可行的, 相比使用单一信息融合方法更科学且合理。
Bayes理论; 多源信息; D-S证据推理; 信息融合; 可靠性评定
0 引言
由于武器装备受到研制周期和研制经费的制约, 系统可靠性试验数量很少, 甚至不做系统试验, 具有典型的小子样复杂系统特点。但武器装备在研制过程中, 由于采用高新技术, 以及试验中设备和手段的进步和多样化, 使试验信息具有多种信息源。另外, 在进行系统可靠性评估时又存在大量的试验信息。从信息论的角度来看, 只有充分利用这些信息, 才能对复杂系统的可靠性有较深刻的认识。
伴随着Bayes理论的兴起, 小子样试验分析方法也得到了长足发展。Bayes方法是一种充分利用先验信息的试验评估方法, 可大大减少所需试验子样数, 节约试验成本, 提高试验效率。在利用Bayes理论进行可靠性评定的过程中, 为了尽可能少做现场试验, 必须充分利用各种先验信息, 但如何合理利用这些多源先验信息, 是小子样理论方法应用中亟待解决的一个问题。
在目前的实际工程应用中, Bayes理论多源信息融合还没有统一的准则, 不同的学者往往会采用不同的融合准则, 由于采用的理论方法不同, 必定会使得信息融合的结果有所差异。基于此, 本文采用证据推理理论, 提出一种适用于Bayes评估的多源信息先验分布融合方法, 将通过各种融合准则获得的先验信息进行再融合, 得到一种合理的综合先验分布。
1 证据推理基本理论

(2)
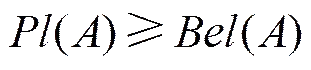
(4)

其中
(6)
该公式是D-S证据理论的核心, 通过它可以把若干条独立的证据结合起来, 它满足交换律和结合律。
2 基于证据推理的Bayes可靠性评定方法
对于复杂系统, 可以获得各种试验信息, 目前, Bayes理论多源信息融合还没有统一的准则, 由于不同的融合准则采用的理论与方法不同, 必定会使得信息融合的结果有所差异, 为此, 本文基于证据推理理论, 将采用各种融合准则获得的先验信息进行再融合。

(8)

采用Dempster规则将mass矩阵中的个mass函数综合为一个统一的mass函数。把前个信息源定义为集合,, 矩阵中前行的个mass函数按Dempster规则产生的综合mass函数记为
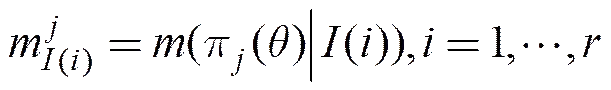
(11)

(13)

(15)
这个mass函数即为证据理论模型的输出,即先验分布的融合权重为

由此可得融合先验分布为
(17)

通过式(11)获得的后验分布就可进行可靠性分析。具体评定原理如图1所示。
3 实例仿真与分析
为验证所建立的评定模型, 引入文献[9]的算例进行分析。已知现场样本数据服从正态分布, 其中, 而未知, 需要通过试验数据确定其取值。为了说明试验数据融合的应用及其合理、有效性, 通过计算机产生一组随机数(其分布为),(5.1139, 6.0668, 5.0593, 4.9044, 4.1677), 相当于实际系统进行了5次现场试验得到的数据。同时, 假设通过历史数据得到的关于未知参数的先验信息数据,(5.020 9, 4.829 7, 5.521 6)(由分布为随机产生),(5.6961, 5.2431, 6.0791)(由分布为随机产生)。下面用本文提出的基于证据推理理论融合方法进行分析。

这样可以获得融合准则的mass矩阵
(20)
由式(10)~式(13), 得
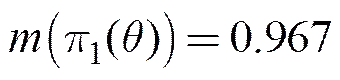
(22)
由此可获得融合后的先验分布为

(24)
根据后验分布, 其对应点估计为5.0385, 非常接近参数的真值5。这足以证明本文方法的有效性和合理性。通过示例也可看出, 该融合方法简便易行, 因而在可靠性试验分析等工程研究领域具有良好的应用前景和推广价值。
4 结束语
本文主要考虑Bayes理论在进行小子样产品可靠性评定时, 需要充分利用各种先验信息。目前, 多源信息融合还没有统一的准则, 融合理论方法的不同会使得融合结果有所差异。本文基于证据推理理论, 提出一种多源信息先验分布融合方法, 将通过各种融合准则获得的先验信息进行再融合, 得到一种合理的综合先验分布, 相比使用单一信息融合方法更科学、合理。本文提出的方法可从该方法理论分析可知, 融合的关键是不同先验分布的加权融合。因此, 本文提出的融合方法适用的条件是先验分布具有线性可加性。因为, 对于某些不具有线性可加性的分布, 一般融合分布是不容易求出的, 使用起来也不一定方便, 这时可以采用近似分布(即统计量的渐进分布), 但会影响融合的效果。本文所建立的方法模型仅通过理论仿真进行了验证, 尚未得到工程应用。在后续的研究中, 将进一步结合工程研制过程中获得的数据开展分析。
[1] Aggarwal, Priyanka. Bayes Predictor of One-parameter Exponential Family Type Population Mean Under Balanced Loss Function[J]. Communications in Statistics Theory and Methods, 2006, 35(8): 1397-1408.
[2] Ali H A, El-Desouky A I, Saleh A I. A Novel Strategy for a Vertical Web Page Classifier Based on Continuous Learning Naive Bayes Algorithm[J]. International Journal of Computers and Applications, 2007, 29(3): 259-277.
[3] 张金槐, 唐雪梅.Bayes方法[M].长沙: 国防科技大学出版社, 1990.
[4] 柴哲丽, 林佳齐, 朱金平.基于贝叶斯的软件可靠性评估研究[J].计算机工程, 2010, 36(2): 73-77. Chai Zhe-li, Lin Jia-qi, Zhu Jin-ping. Research on Software Reliability Evaluation Based on Bayes[J]. Computer Engineering, 2010, 36(2): 73-77.
[5] 张士峰, 蔡洪.Bayes分析中的多源信息融合问题[J].系统仿真学报, 2000, 12(1): 54-56.Zhang Shi-feng, Cai Hong. Fusion of Information of Multiple Sources in Bayesian Analysis[J]. Journal of System Simulation, 2000, 12(1): 54-56.
[6] 张湘平.小子样统计推断与融合理论在武器系统评估中的应用研究[D].长沙: 国防科学技术大学, 2003.
[7] 冯静, 周经伦, 孙权.Bayes分析中多源验前信息融合的ML_II方法[J].数学的实践与认识, 2006, 36(6): 142-145.Feng Jing, Zhou Jing-lun, Sun Quan. Fusion of Information of Multiple Sources Based on ML-II Theory in Bayesian Analysis[J]. Mathematics in Practice and Theory, 2006, 36(6): 142-145.
[8] 杨春, 李祖怀.一个证据理论模型及其在专家意见综合中的应用[J]. 系统工程理论与实践, 2001, 21(4): 43-48. Yang Chun, Li Zu-huai. An Evidence Reasoning Model with Its Application to Expert Opinions Combination[J]. Systems Engineering-Theory & Practice, 2001, 21(4): 43-48.
[9] 冯静.小子样复杂系统可靠性信息融合方法与应用研究[D]. 长沙: 国防科学技术大学, 2004.
(责任编辑: 陈 曦)
A Bayesian Reliability Evaluation Method Based on Dempster-Shafer Evidence Theory
ZHAO Fang-ze
(College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China)
Bayesian method is an important and suitable approach for system reliability evaluation in small sample circumstance. In order to reduce the testing data, all kinds of a priori information must be used, so the information fusion of multiple sources becomes a key problem in Bayesian analysis. A new method based on the Dempster-Shafer evidence theory is proposed to realize the information fusion of multiple sources, which can integrate more a priori distributions obtained through different fusion criteria. Simulation shows that the proposed method is effective.
Bayesian theory; information of multiple sources; Dempster-Shafer evidence theory; information fusion; reliability evaluation
TJ.630.1; TB114.3
A
1673-1948(2013)03-0175-04
2013-01-29;
2013-03-27.
赵仿泽(1964-), 男, 在读博士, 主要研究领域为系统工程理论与方法.
