梯度变化对密度梯度蜂窝材料力学性能的影响＊

吴鹤翔，刘 颖

（北京交通大学土木建筑工程学院力学系，北京 100044）

随着蜂窝材料在防护结构中的应用，一些关键性的问题的解决，如冲击初始应力峰值的抑制和冲击应力强化的控制等，对蜂窝材料的性能设计提出了进一步的要求。冲击过程中材料内的应力分布和能量吸收过程的控制成为蜂窝材料性能设计的关键问题之一。

蜂窝材料的动力学性能与其相对密度密切相关，对于质量一定的蜂窝材料，改变密度在空间的排布为实现材料的动力学响应控制提供了可能。如何根据使用要求来设计密度的空间分布成为梯度蜂窝材料设计中的一个关键问题［1－2］。刘颖和张新春等［3－6］基于功能梯度的概念，建立了密度梯度蜂窝材料模型，通过改变单胞的几何尺寸来控制材料的密度梯度排布；在此基础上，基于一维应力波理论，建立了一定密度梯度下，梯度排布与冲击速度之间的关系。但是，对于质量一定的蜂窝材料，在相同密度排布的基础上，密度梯度的大小对材料动力学响应的影响并未深入讨论，而这对于材料密度梯度的优化设计是十分重要的。

本文中，通过改变密度梯度的大小，讨论密度梯度的变化对材料能量吸收特性的影响，以期进一步完善蜂窝材料的密度梯度设计理论。

1 计算模型

密度梯度圆环蜂窝材料的计算模型如图1所示。试件由4层具有不同壁厚但是相同外径的圆环组成，每层包括5排相同的圆环。通过改变不同层圆环的壁厚可控制蜂窝材料的密度梯度。计算模型的层数和每层中圆环的数量、圆环的半径和厚度均可根据实际工程中的需要设计。

基于图1所示的计算模型，采用显式动力学有限元软件LS－DYNA［7］对面内冲击动力学响应特性进行研究。如图1所示，蜂窝试件置于底端固定刚性板上，试件两侧自由。顶端刚性板以某一初始速度沿y方向运动。为保证试件处于平面应变状态，在计算过程中，约束所有节点沿z方向的位移。通过收敛性分析，每个圆环选用32个shell 163单元（4节点四边形壳单元）进行离散，沿壳厚度方向取5个积分点以保证计算精度。在压缩过程中，所有可能接触的表面均定义为自由接触表面。刚性板与蜂窝试件的外表面光滑接触无摩擦。圆环的基体材料为铝，采用理想弹塑性模型。主要材料参数为：密度ρs＝2.7g／m3，杨氏模量Es＝69GPa，泊松比μ＝0.3，屈服强度σys＝76MPa。试件的尺寸为L1×L2＝2n1R×2n2R，其中R 为圆环的外半径，n1和n2分别表示沿x和y方向圆环的数量。为了消除尺寸效应［8］，取n1＝10，n2＝20，R＝5mm。此时，蜂窝材料的相对密度为

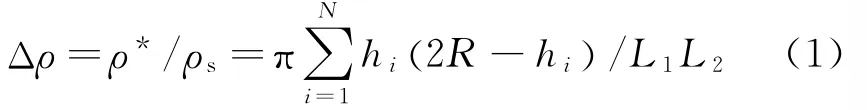
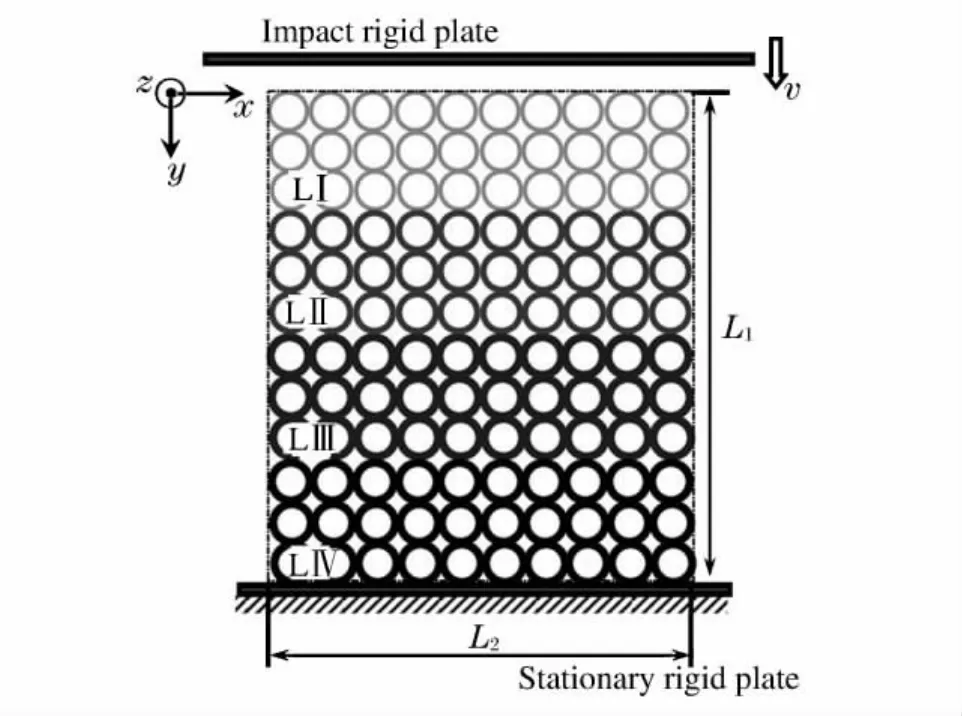
图1 密度梯度圆环蜂窝材料计算模型示意图Fig.1 Calculating model of the density graded circular honeycomb

式中：ρ＊表示蜂窝材料的密度，N 为圆环总数，hi为第i个圆环的壁厚。

基于2种梯度排布方式（其他梯度排布方式的影响参考文献［5］），即从冲击端到固定端各层圆环相对密度递增排布以及各层圆环相对密度递减排布，讨论3种梯度大小的密度梯度蜂窝材料（记为GⅠ、GⅡ和GⅢ，材料相对密度保持不变）的面内冲击性能。1～4层圆环对应的壁厚分别为：GⅠ：0.39、0.46、0.54、0.61mm；GⅡ：0.31、0.44、0.56、0.69mm；GⅢ：0.24、0.41、0.59、0.76mm。另外，为了进行参考，文中还同时给出了具有相同相对密度的均匀圆环蜂窝材料（记为G0）的响应特性（此时圆环壁厚均为0.5mm）。

2 计算结果和分析

2.1 均匀圆环蜂窝材料的响应特性

如图1所示，当所有圆环的壁厚相同时，即为均匀圆环蜂窝材料。图2给出了不同冲击速度下均匀圆环蜂窝材料的平台应力值。这里，平台应力

式中：εcr是与准静态塑性坍塌应力σcr对应的应变值，εD为致密化应变。

基于一维冲击波理论，P.J.Tan等［9－10］和S.R.Reid等［11］建立了均匀多孔材料平台应力与冲击速度之间的关系，即

式中：v为冲击端刚性板的冲击速度。这里将此公式推广到圆环蜂窝材料。参考文献［12］，致密化应变εD和σcr分别为

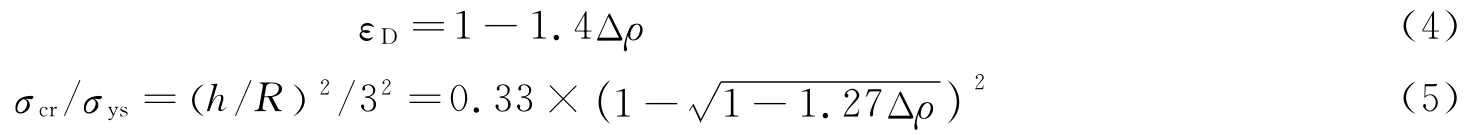
式中：h为圆环壁厚。将方程（4）～（5）代入方程（3）中，不同冲击速度下，均匀圆环蜂窝材料的平台应力

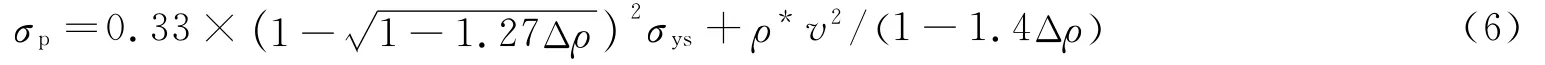
根据方程（6），不同冲击速度下均匀圆环蜂窝材料平台应力的理论值如图2中实线所示。比较计算结果和理论结果可以发现，二者吻合较好。

2.2 密度梯度圆环蜂窝材料的动力学响应

文献［3－6］中已经对不同梯度排布下蜂窝材料的动力响应进行了讨论，由于篇幅限制，图3仅给出不同冲击速度下，从冲击端到固定端密度递增情况下试件冲击端的名义应力应变关系曲线和从冲击端到固定端密度递减情况下试件固定端的名义应力应变关系曲线。这里名义应力定义为刚性板反力与试件初始横截面面积（L2×1mm）之比，名义应变定义为试件的压缩量与其初始长度L1之比。

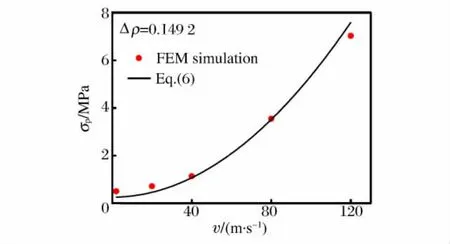
图2 不同冲击速度条件下均匀圆环蜂窝材料的平台应力值Fig.2 Plateau stresses with respect to the impact velocity at the impact end for the uniform circular honeycombs

如图3所示，在低速冲击下，与均匀圆环蜂窝材料相同，冲击端应力随压缩量的增加逐渐增加。但是在高速冲击下，蜂窝材料表现出从冲击端到固定端逐层压溃的变形模式。由于质量分布在空间呈梯度变化，虽然总的相对密度相同，密度梯度圆环蜂窝材料的动力响应表现出分段平台特性。高密度层对应着较高的应力平台。随着冲击速度和密度梯度的增加，分段特性更加明显。分段应力平台的相对长度近似等于

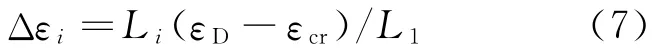
式中：Li为密度梯度圆环蜂窝材料中第i层的厚度。如图3所示，高速冲击下，密度梯度递减的蜂窝材料输出端的应力水平低于均匀排布结构，且密度梯度越大，应力值越低，这体现了通过密度梯度的设计，蜂窝材料能有效地控制传入被保护结构内的应力水平。

图3 密度梯度圆环蜂窝材料冲击端和输出端的动力学响应Fig.3 Dynamic properties of DGCH at the impact and distal ends

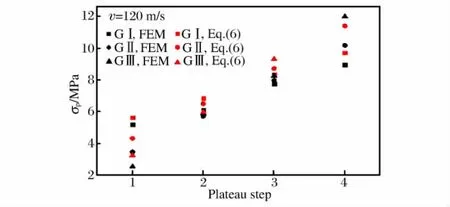
图4 高速冲击条件下密度梯度圆环蜂窝材料的平台应力值Fig.4Step plateau stresses of DGCH under high impact velocity

图4给出了高速（v＝120m／s）冲击下，不同密度梯度蜂窝材料的平台应力值。其中，横坐标1对应着相对密度最小层的平台值（平台应力值最低），而4对应着相对密度最大层的平台值（平台应力值最高）。同时，基于方程（6），图4中还给出了梯度蜂窝材料不同密度层的理论平台应力值（对于每层而言密度是均匀的）。对比计算和理论结果可以看出，虽然方程（6）给出的平台应力值稍高于数值模拟结果（小于10%），但是可以近似预测梯度蜂窝材料各层的平台应力值。

2.3 密度梯度圆环蜂窝材料的能量吸收特性

图5为不同密度梯度的蜂窝材料及具有相同相对密度的均匀蜂窝材料单位质量吸收的能量，即

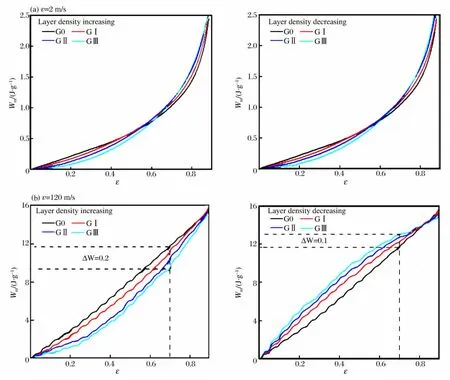
图5 不同冲击速度下密度梯度圆环蜂窝材料吸收的能量Fig.5 Energy absorption of DGCH under different impact velocities

对于密度梯度蜂窝材料，

如图5所示，在低速冲击下，在变形初期，梯度蜂窝材料的能量吸收率低于具有相同相对密度的均匀蜂窝材料，且密度梯度越大，能量吸收效率越低（见图5（a））。但是随着压缩量的增加，梯度蜂窝材料的能量吸收率高于均匀蜂窝材料的能量吸收率。在高速冲击下，对于相对密度从冲击端到固定端递增的情况，材料的能量吸收效率低于具有相同相对密度的均匀蜂窝材料，且梯度越大，效率越低。如图5（b），在ε＝0.7时，试件GⅢ相对于均匀材料单位质量能量吸收效率低20%（ΔW ＝（WG0－WGⅢ）／WG0）。但是，对于相对密度从冲击端到固定端递减的情况，梯度蜂窝材料表现出更高的能量吸收效率，且密度梯度越大，单位质量材料吸收的能量越多。如图5（b）所示，在ε＝0.7时，试件GⅢ比均匀蜂窝材料单位质量能量吸收效率高10%。另外从图中可以看出，不同密度梯度蜂窝材料在致密化应变时吸收的能量相同。

3 结 论

基于二维密度梯度圆环蜂窝材料，讨论了相对密度一定的情况下，密度梯度大小对蜂窝材料动力学响应特性的影响。计算结果表明，对于从冲击端到固定端密度递减的蜂窝材料，密度梯度增加将降低输出端的应力水平。低速冲击条件下，梯度系数越大，材料单位质量能量吸收效率越低；但是在高速冲击下，在致密化以前，梯度系数越大，材料单位质量能量吸收率越高。该结论对于进一步确定密度梯度对材料动力学响应的影响具有积极意义。

［1］Gupta N.A functionally graded syntactic foam material for high energy absorption under compression［J］.Materials Letters，2007，61（4／5）：979－982.

［2］Zeng H B，Pattofatto S，Zhao H，et al.Impact behaviour of hollow sphere agglomerates with density gradient［J］.International Journal of Mechanical Sciences，2010，52（5）：680－688.

［3］刘颖，何章权，吴鹤翔，等.分层递变蜂窝材料面内冲击性能的研究［J］.爆炸与冲击，2011，31（3）：225－231.Liu Ying，He Zhang－quan，Wu He－xiang，et al.In－plane dynamic crushing of functionally layered metal honeycombs［J］.Explosion and Shock Waves，2011，31（3）：225－231.

［4］张新春，刘颖.密度梯度蜂窝材料动力学性能研究［J］.工程力学，2011，29（8）：372－377.Zhang Xin－chun，Liu Ying.Research on the dynamic crushing of honeycombs with density gradient［J］.Engineering Mechanics，2011，29（8）：372－377.

［5］Liu Ying，Wu He－xiang，Lu G X，et al.Dynamic properties of density graded thin－walled metal hollow sphere arrays［J］.Mechanics of Advanced Materials and Structures，dio：10.1080／15376494.2011.627642.

［6］Liu Ying，Wu He－xiang，Wang Bin.Gradient design of metal hollow sphere（MHS）foams with density gradients［J］.Composites：Part B，2012，43（3）：1346－1352.

［7］LSTC.LS－DYNA keyword user’s manual［M］.Livermore Software Technology Corporation，2007.

［8］Gibson L J.Mechanical behaviour of metallic foams［J］.Annual Review of Materials Science，2000，30（1）：191－227.

［9］Tan P J，Reid S R，Harrigan J J，et al.Dynamic compressive strength properties of aluminum foams.Part IIShock theory and comparison with experimental data and numerical models［J］.Journal of the Mechanics and Physics of Solids，2005，53（10）：2206－2230.

［10］Tan P J，Reid S R，Harrigan J J，et al.Dynamic compressive strength properties of aluminium foam.Part I－Experimental data and observations［J］.Journal of the Mechanics and Physics of Solids，2005，53（10）：2174－2205.

［11］Reid S R，Peng C.Dynamic uniaxial crushing of wood［J］.International Journal of Impact Engineering，1997，19（5／6）：531－570.

［12］Gibson L J，Ashby M F.Cellular solid：Structure and properties［M］.2nd ed.Cambridge：Cambridge University Press，1997.