周期分布缺陷对韧性材料高应变率拉伸碎裂过程的影响＊

郑宇轩，周风华，胡时胜

（1.中国科学技术大学中国科学院材料力学行为和设计重点实验室，安徽 合肥 230026；2.宁波大学教育部冲击与安全工程重点实验室，浙江 宁波 315211）

材料在冲击载荷作用下常常会断裂成多个碎片，对材料动态碎裂机制的研究是应用物理学、力学、航天和兵器工程等领域共同关心的课题。对于给定材料在给定载荷作用下碎裂时产生碎片的尺寸，D.E.Grady和M.E.Kipp［1－5］针对金属、岩石等多种材料进行了大量实验，并从物理机制上对碎裂现象进行了理论分析，提出了有关碎片尺寸的计算公式。

针对韧性金属材料，M.E.Kipp等［3］将一个与断裂能量相关的内聚断裂模型引入Mott的卸载波传播分析，推导出一个预测韧性材料拉伸碎裂过程中产生碎片的平均尺度的公式。为检验该公式的适用性，郑宇轩等［6］利用ABAQUS／Explicit动态有限元软件模拟了一维应力状态下的弹塑性金属（45钢）杆在高应变率拉伸变形过程中的碎裂现象，并研究了Grady－Kipp公式中的关键参数如材料密度、应变率和材料断裂能对碎裂过程的影响。研究结果表明：Grady－Kipp公式在广泛的材料参数和应变率范围内能较好地预测碎裂过程中产生的碎片的平均尺寸。

在数值模拟过程中，一个几何尺寸和外载荷完全均匀的受拉伸杆，最终断（碎）裂的发生位置取决于计算模型的非均匀性。文献［6］中研究的是一个理想的、没有任何缺陷的物理模型，导致碎裂发生的初始缺陷来自幅度极小的随机单元网格差异。事实上，金属材料在制造过程中引入的杂质可能引起材料的制造缺陷，在机械加工过程中也可能导致表面的几何缺陷，多晶金属材料中较大的晶粒还会导致材料在微观／介观尺度上产生不均匀性等。这些不可避免的偏差或缺陷的幅度较大，且具有一定的空间分布特征。学者们［7－8］对这些自然产生的初始缺陷对材料的长期疲劳寿命和在结构中抗压及屈曲特性的影响也进行了一些研究，但有关缺陷对在冲击载荷作用下材料的断（碎）裂影响的研究却并不多见。周风华和段忠等［9－10］曾针对于脆性材料，利用特征线数值计算方法研究了具有不同周期特征初始缺陷的一维脆性杆在高应变率变形下的碎裂问题，计算结果表明，对于脆性材料，空间分布完全随机的初始缺陷对细长杆碎裂中产生的碎片个数影响不大；而对于具有等间距初始缺陷的细长杆，碎片个数在一定的应变率区域内完全由初始缺陷个数控制。韧性金属材料中初始缺陷对其断（碎）裂过程的影响是否和脆性材料相似，需进一步研究。

本文中，沿用前期工作［6］的计算模型和材料参数，分析一个直径具有一定周期分布的一维圆杆在高速拉伸变形时的碎裂过程。圆杆的横截面半径沿轴向为周期性正弦曲线，以此代表外表面的正弦几何缺陷。通过改变正弦几何缺陷的波长和幅值，分析周期性缺陷对细长杆碎裂过程、碎片个数的影响。进一步简要分析双幅值复合几何缺陷对细长杆碎裂过程的影响。研究结果可以对爆炸与冲击工程应用，如刻槽式破片战斗部设计、定向爆破等实际问题提供参考。

1 有限元模型

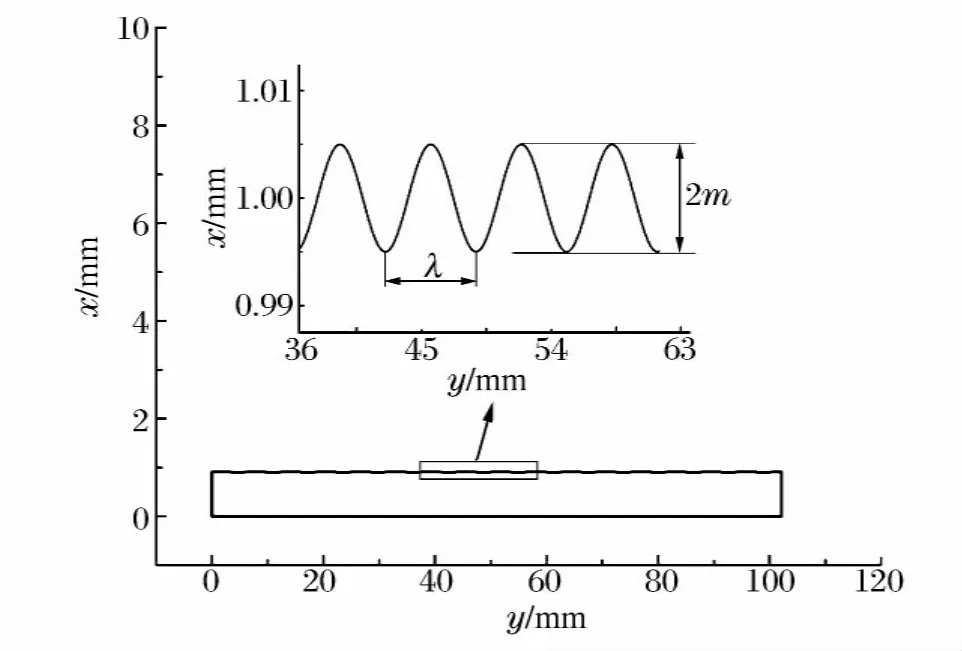
图1 处于一维应力状态，粗细不均匀的弹塑性细长圆杆的剖面图Fig.1 Cross section of thin bars in states of 1Dstress with the initial sinusoidal geometric defects

选取一维应力状态的45钢弹塑性圆柱杆作为有限元模拟对象，杆长L＝100mm，横截面平均直径D＝1mm（半径为r）。采用几何非均匀性模拟初始缺陷，将圆柱杆的原为直线的母线施加周期性扰动，形成外表面具有等间距的正弦几何缺陷的粗细不均匀圆柱体，如图1所示。在计算过程中，沿圆杆轴向方向施加线性分布的初始速度，可以避免突加载荷时产生应力波干扰，使得圆杆在Mott卸载波产生前始终承受均匀的拉伸应变率（速度梯度）。采用Johnson－Cook热黏塑性本构模型描述材料的动态变形和热软化特性，采用包含内聚力失稳断裂准则的Johnson－Cook型损伤断裂模型描述材料的破坏，分别处理损伤开动和演化过程。用一个等效塑性应变作为损伤D的开动准则，损伤开动的临界应变εd与应力三轴度、应变率和温度相关，一旦损伤开动，就可采用断裂能量判据来判断单元是否失效。一旦单元内部损伤达到1，材料完全破坏，可采用单元消去技术将失效单元从整体结构中消去。详细材料模型和参数见文献［6］。

2 数值模拟及结果分析

2.1 周期性初始缺陷对一维应力杆碎裂过程的影响

利用ABAQUS／Explicit有限元程序对具有周期性初始几何缺陷的一维圆杆拉伸碎裂过程进行数值模拟，预设正弦分布的缺陷的波长（即缺陷间距）l＝5mm（在L＝100mm的杆上相当于有L／l＝20个周期）、幅值m＝0.005mm（m／r＝0.01，相当于1%的初始扰动）的初始缺陷。

计算表明，具有初始缺陷的韧性金属杆在不同应变率下表现出不同的变形和断裂特性，图2给出了具有周期性初始几何缺陷的一维圆杆在3种不同的恒定拉伸速度下的碎裂情况。恒定拉伸速度v0＝800m／s时（初始应变率8×103s－1），细长杆的所有初始缺陷均发展成颈缩，其中的一部分颈缩最终断裂，碎片尺寸通常为1个或2个被拉长了的颈缩间距。并且初始缺陷会在一定程度上抑制细长杆其他位置颈缩的生成（碎片中所含明显颈缩区域均为初始缺陷位置）。恒定拉伸速度v0＝2km／s（初始应变率2×104s－1）时，细长杆的初始缺陷均发展成颈缩并最终全部断裂，细长杆断裂位置完全由初始缺陷控制，碎片尺寸恰好为1个被拉长了的颈缩间距。恒定拉伸速度v0＝8km／s（初始应变率8×104s－1）时，不仅细长杆的初始缺陷均发展成颈缩并最终全部断裂，杆的其他位置也有若干颈缩生成，并部分发生断裂，碎片尺寸小于或等于1个被拉长了的颈缩间距。

图2 不同恒定拉伸速度下一维应力杆碎裂后的形态Fig.2 Fragmentized 1Dstress bars with initial defects under different pulling velocities

从断裂时间来看，与不施加初始缺陷的细长杆相比，具有周期性初始缺陷的杆在较低的同等拉伸速度下断（碎）裂现象一般都提前发生，如图3（a）所示。其原因在于：在拉伸过程中，人为施加的初始缺陷位置的横截面积偏小而诱发应力集中，造成杆提前进入非均匀塑性变形阶段（颈缩），使得细长杆提前断（碎）裂。然而随着应变率的提高，如当初始应变率达到8×104s－1时，由于杆的拉伸速度很快，初始缺陷对引发颈缩和断裂来说不起主导作用，细长杆其他位置同样也能发展出颈缩以及断裂。此时具有初始缺陷的细长杆断（碎）裂时间和无初始缺陷的细长杆基本一致，如图3（b）所示。陈磊等［11］曾采用数值模拟方法分析了无氧铜圆环的爆炸膨胀碎裂过程，得到的圆环试件碎裂发生的临界初始膨胀速度（150m／s）高于实验结果（110m／s），差异可能来自真实试件中的加工缺陷。

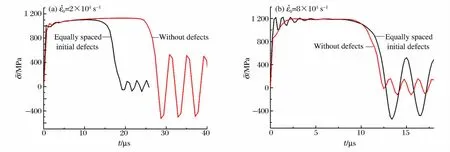
图3 有无初始缺陷的一维应力杆的平均应力历史曲线Fig.3 Average stress histories of thin bars in states of 1Dstress

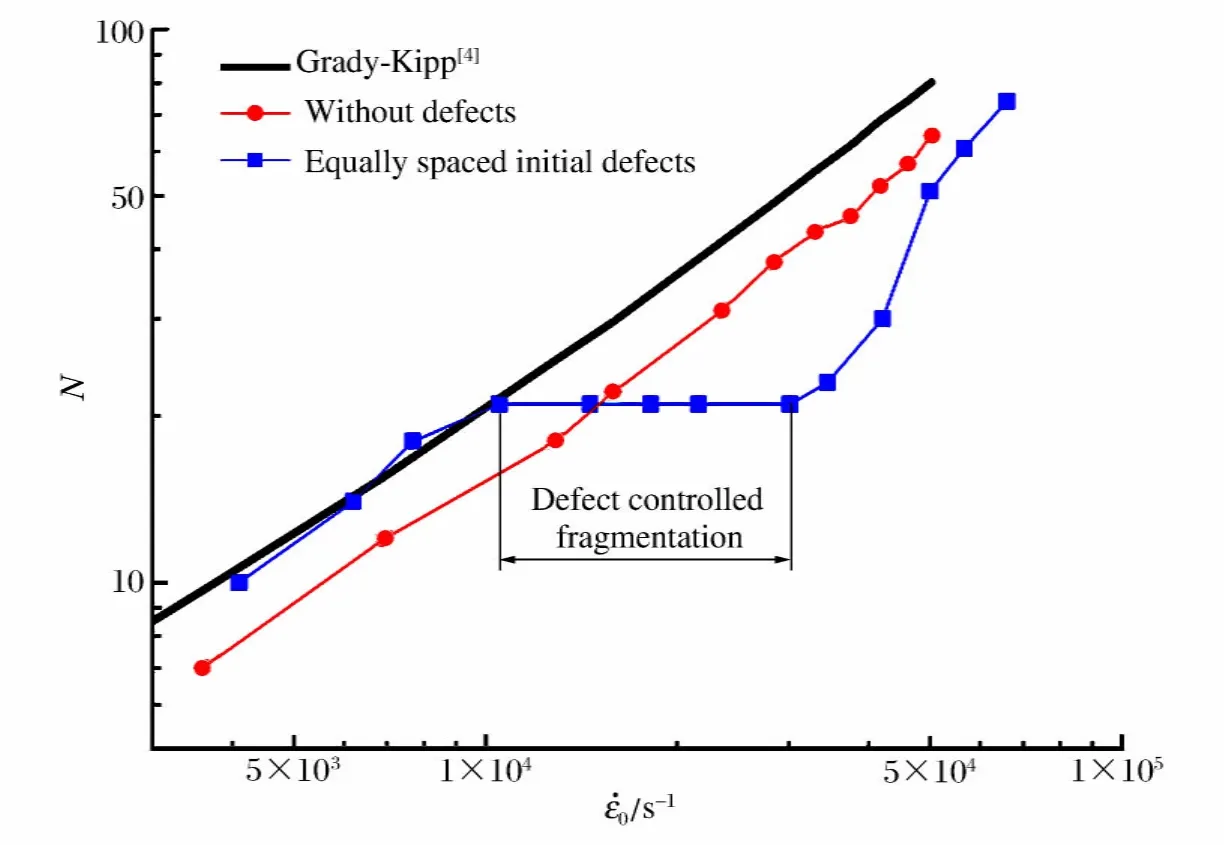
图4 不同应变率下一维应力杆碎片数Fig.4 Fragment numbers of thin bars in states of 1Dstress at different strain rates

可见，周期性初始缺陷对细长杆在高应变率拉伸碎裂过程的影响表现出明显的应变率依赖性。为了研究周期性初始缺陷在一个更广泛的应变率范围内对细长杆碎裂过程的影响，分别进行了初始应变率为5×103～1.5×105s－1的数值计算（在发生碎裂时刻，由于杆已被拉长，对应的实际应变率为4.1×103～6.6×104s－1）。图4给出了不同应变率下周期性初始缺陷对细长杆碎裂后碎片个数N的影响，横坐标为断裂时刻实际应变率（除特别注明外，下文各图中的应变率均采用断裂时刻实际应变率）。可以看出，初始缺陷将应变率大致分为3个区域：

（2）在中间应变率区域（断裂时刻实际应变率104≤≤3×104s－1），初始缺陷完全控制了细长杆碎裂过程产生的碎片个数，在此区域，细长杆碎片个数等于初始缺陷个数，与应变率无关。我们称在这个应变率范围，材料的碎裂过程为缺陷控制碎裂（defect controlled fragmentation）；

2.2 不同波长的周期性缺陷对一维应力杆碎裂过程的影响

图5 具有不同间距的缺陷的一维应力杆碎片个数与应变率的关系Fig.5 Fragment number of thin bars in states of 1Dstress with different cycles vs.strain rate

在周期性缺陷结构下，缺陷间距由正弦波波长l决定。为了探讨周期性初始缺陷的波长对细长杆碎裂过程的影响，选取初始缺陷幅值相同（m／r＝1%的初始扰动）而波长不同（分别为10、20、30个周期；l＝10，5，3.33mm）的3种模型进行数值计算。计算结果如图5所示，可以看出，不同波长的周期性初始缺陷对一维应力杆碎裂过程均表现出相似的作用，均存在一个由初始缺陷完全控制碎片个数，即发生缺陷控制碎裂的应变率区域（窗口），宽度近似为半个数量级（实际应变率相差约3倍）。随着初始缺陷个数的增多（等间距缺陷间距变小），初始缺陷完全控制一维应力杆碎裂的应变率区域整体往高应变率方向平移。

图6给出了不同波长下的初始缺陷对细长杆平均应力历史的影响。在初始应变率为2×104s－1时（对应实际应变率约1.5×104s－1），20周期和30周期初始缺陷的细长杆较无初始缺陷的细长杆碎裂时间明显提前，而10周期初始缺陷的细长杆和无初始缺陷的细长杆碎裂时间相近。造成此现象的主要原因是2×104s－1的应变率恰巧落于20周期和30周期初始缺陷的“缺陷控制碎裂”窗口的应变率范围以内，而大于10周期初始缺陷的“缺陷控制碎裂”窗口的应变率（从图5可以看出）。从图3的结果可以知道，如果施加应变率落在初始缺陷不起主导作用的区域时，初始缺陷对细长杆的碎裂发生的时间的影响效果很有限。

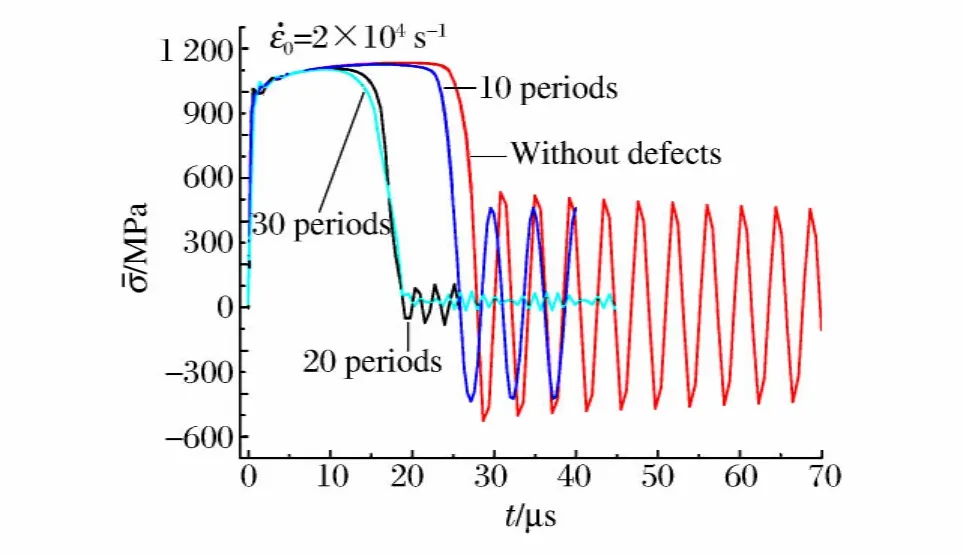
图6 具有不同缺陷间距缺陷的一维应力杆应力历史Fig.6 Histories of the average stress in thin bars in states of 1Dstress with different defect spacings

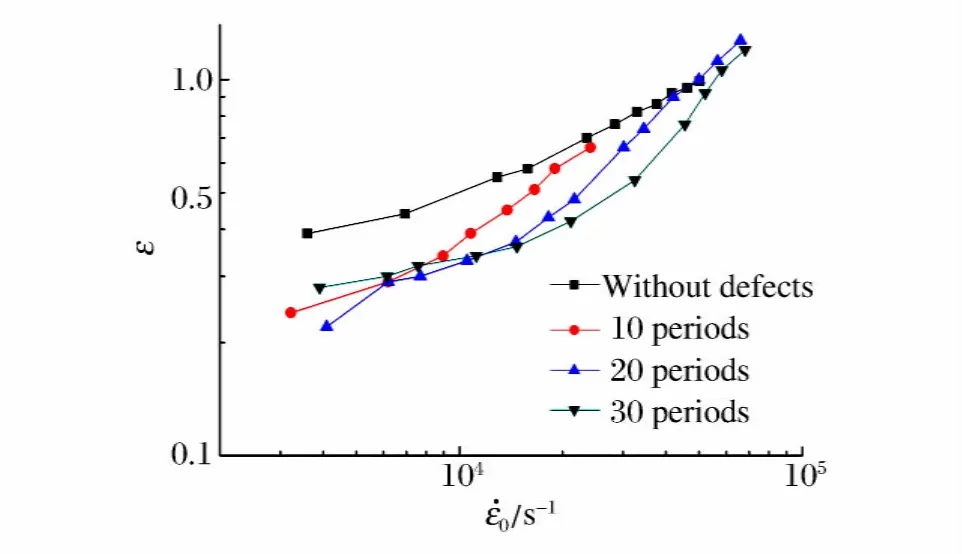
图7 具有不同缺陷间距缺陷的一维应力杆表观断裂应变和应变率的关系Fig.7 Strain of thin bars in states of 1Dstress with different cycles vs.strain rate

细长杆中存在初始几何缺陷的位置由于应力集中使得颈缩优先在此形成并发展，从而细长杆整体经历的均匀变形阶段提早结束，最终圆杆的表观断裂应变变小。如图7所示，所有缺陷间距的周期性初始缺陷细长杆的表观断裂应变均比无缺陷的小，但随着应变率的持续提高，周期性初始缺陷对细长杆的表观断裂应变的影响逐渐减小，最终与无初始缺陷的细长杆表观断裂应变一致。并且初始几何缺陷间距越小，细长杆表观断裂应变趋同所需的应变率越高。

2.3 不同幅值的周期性缺陷对一维应力杆碎裂过程的影响

固定缺陷个数为20个，分别对初始缺陷幅值为0.002 5、0.005、0.02mm（m／r ＝ 0.5%，1%，4%的初始扰动）的3种模型进行数值计算。计算结果如图8所示，在发生“缺陷控制碎裂”时，碎片个数均为21。但随着初始扰动的加大，“缺陷控制碎裂”窗口的应变率区域也相应变宽，这表明缺陷的影响程度越来越大。

图8 具有不同幅值缺陷的一维应力杆碎片个数和应变率的关系Fig.8 Fragment number of thin bars in states of 1Dstress with different disturbance vs.strain rate

图9给出了不同幅值下的初始缺陷对细长杆的平均应力历史的影响。初始扰动越大，杆引发颈缩并快速发展导致断裂的时间越早，最终断（碎）裂时间越提前。

图10给出了不同幅值下的初始缺陷对细长杆表观断裂应变的影响。可以看出，在模拟的应变率范围内，具有较大初始扰动的细长杆的表观断裂应变始终比具有较小的初始扰动的细长杆表观断裂应变小，并没有表现出类似于研究不同波长的初始缺陷时出现的趋同现象。

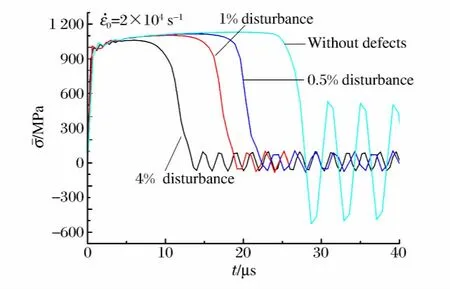
图9 具有不同幅值缺陷的一维杆平均应力历史曲线Fig.9 Histories of the average stress in thin bars in states of 1Dstress with different disturbance

图10 具有不同幅值缺陷的一维杆表观断裂应变和应变率的关系Fig.10 Strain of thin bars in states of 1Dstress with different disturbance vs.strain rate

2.4 复合缺陷对一维应力杆碎裂过程的影响

上述研究是对简单的、单周期等幅值几何缺陷进行的。事实上，材料的初始缺陷未必是一个简单的等幅值分布，现简单讨论具有2种不同幅值的复合缺陷对细长杆碎裂过程的影响。初始缺陷仍然是等间距分布（20周期），但是幅值不一致，间隔地分别赋予不同幅值的初始扰动（m／r分别为0.5%和1%），如图11所示。

图12给出了具有图11所示的复合初始缺陷的细长杆产生碎片的个数随施加应变率的变化曲线。与图4所示的单个幅值的正弦初始缺陷相比，复合初始缺陷并不单纯地将应变率分成“低应变率区域”、“缺陷控制碎裂窗口”和“高应变率区域”等3个区域。在原有的缺陷控制碎裂窗口的应变率区域出现了一个跃阶，将原有的缺陷完全控制窗口一分为二。在窗口的前部分区域，幅值较大的初始缺陷（1%的初始扰动）起主导作用，而后部分区域为两者（1%的初始缺陷和0.5%初始缺陷）共同控制区域。

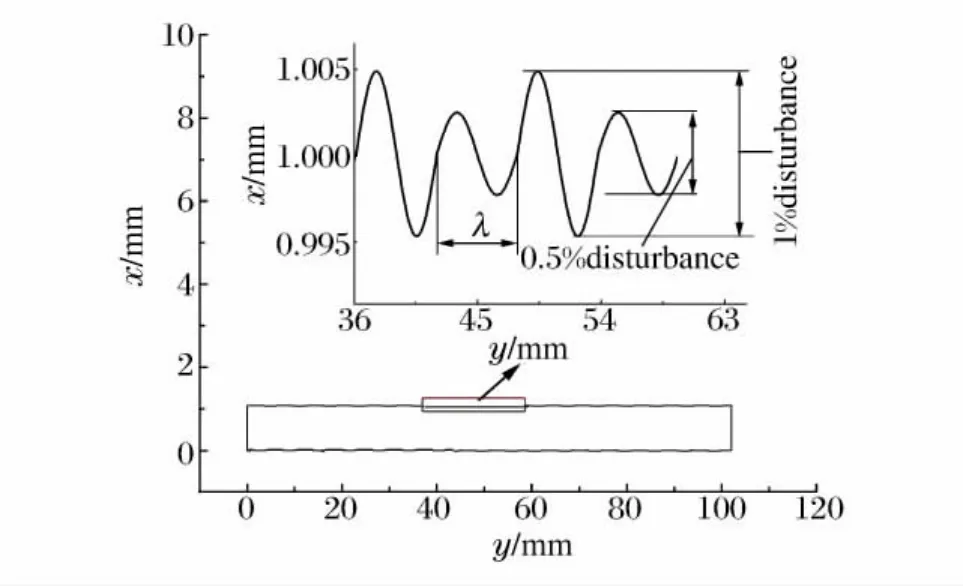
图11 复合缺陷的一维应力杆的剖面图Fig.11 Cross section of thin bars in states of 1Dstress with combined defects

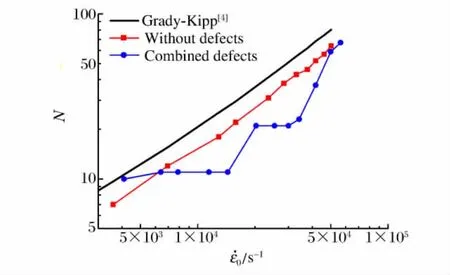
图12 具有复合缺陷的一维杆碎片个数与应变率的关系Fig.12 Fragment number of thin bars in states of 1Dstress with the combined defects vs.strain rate

3 结 论

（1）具有周期性初始缺陷的细长杆与无初始缺陷的细长杆相比，在同等拉伸速度下断（碎）裂现象一般提前发生。缺陷对碎裂过程产生的碎片个数和尺寸有明显影响。在一定应变率窗口内，周期性初始缺陷完全控制了细长杆的碎裂过程和碎片个数，此时称材料发生“缺陷控制碎裂”。

（2）随着初始缺陷的个数增多（缺陷间距减小），发生“缺陷控制碎裂”的应变率窗口整体往高应变率方向移动，表观断裂应变趋同所需要的应变率幅值也相应提高。随着初始扰动的增加（缺陷增大），“缺陷控制碎裂”窗口的应变率范围加宽，细长杆断（碎）裂时间提前，碎裂时刻杆的表观应变也变小。

（3）如果存在2类大小不同的初始缺陷，则随着应变率的提高，高幅值缺陷首先起作用，低幅值缺陷在更高的应变率下才发挥作用。在极高的应变率下，材料的初始缺陷的影响都被削弱。可以预计，更复杂的空间分布缺陷将打乱“缺陷控制碎裂”的窗口，导致碎片个数与施加应变率之间呈单调增加的关系。

在涉及强动载荷作用的实际工程中，有时会主动在结构元件中引入规则缺陷，造成结构的特定破碎模式。本文中辨识“缺陷控制碎裂”现象以及发生这种现象的应变率窗口，对工程设计有指导作用。

［1］Grady D E.Fragmentation of solids under impulsive stress loading［J］.Journal of Geophysics Research，1981，86（B2）：1047－1054.

［2］Grady D E.Local inertial effects in dynamic fragmentation［J］.Joural of Applied Physics，1982，53（1）：322－325.

［3］Kipp M E，Grady D E.Dynamic fracture growth and interaction in one－dimension［J］.Journal of Mechanics and Physics of Solids，1985，33（4）：399－415.

［4］Grady D E，Kipp M E.Experimental measurement of dynamic failure and fragmentation properties of metals［J］.International Journal of Solids and Structures，1995，32（17／18）：2779－2991.

［5］Grady D E，Olsen M L.A statistics and energy based theory of dynamic fragmentation［J］.International Journal of Impact Engineering，2003，29（1／2／3／4／5／6／7／8／9／10）：293－306.

［6］郑宇轩，胡时胜，陈磊，等.材料参数对韧性材料高应变率拉伸碎裂过程的影响［J］.固体力学学报，2012，43（5）：861－870.Zheng Yu－xuan，Hu Shi－sheng，Chen Lei，et al.Effect of material properties on the fragmentation of ductile materials under high strainrate tension［J］.Acta Mechanica Solida Sinica，2012，43（5）：861－870.

［7］Kudish Ilya I.Fatigue modeling for elastic materials with statistically distributed defects［J］.Journal of Applied Mechanics，2007，74（6）：1125－1133.

［8］向红，傅衣铭.损伤对具初始缺陷压杆蠕变后屈曲路径的影响［J］.固体力学学报，2004，25（2）：229－232.Xiang Hong，Fu Yi－ming.Effect of damage on postbuckling of a compressed column with initial imperfection［J］.Acta Mechanica Solida Sinica，2004，25（2）：229－232.

［9］Zhou F，Molinari J F，Ramesh K T.A cohesive－model based fragmentation analysis：Effects of strain rate and initial defects distribution［J］.International Journal of Solids and Structures，2005，42（18／19）：5181－5207.

［10］段忠，周风华.缺陷对脆性材料碎裂过程的影响［J］.爆炸与冲击，2013，33（1）：11－20.Duan Zhong，Zhou Feng－hua.Effects of defects on the fragmentation process of brittle materials［J］.Explosion and Shock Waves，2013，33（1）：11－20.

［11］陈磊，周风华，汤铁钢.韧性金属圆环高速膨胀碎裂过程的有限元模拟［J］.力学学报，2011，43（5）：861－870.Chen Lei，Zhou Feng－hua，Tang Tie－gang.Finite element simulations of the high velocity expansion and fragmentation of ductile metallic rings［J］.Acta Mechanica Sinica，2011，43（5）：861－870.