多功能含能结构材料冲击压缩特性的理论计算*
2013-09-19史安顺张先锋
史安顺,张先锋,乔 良,魏 胜,张 将,何 源,何 勇
(1.南京理工大学智能弹药技术国防重点学科实验室,江苏 南京 210094;2.中国兵器科学研究院宁波分院,山东 烟台 264003;3.安徽红星机电公司,安徽 合肥 231135)
多功能含能结构材料(multifunctional energetic structural materials,MESMs)又称含能金属材料或反应金属材料,是指将一种或多种金属材料以一定的工艺方法组合形成的具有一定强度和反应特性的双功能结构材料。这类材料可以是铝热剂、金属间化合物、金属/聚合物混合物、亚稳态分子化合物、复合材料和氢化物等[1]。由于具有冲击反应释能特性,MESMs可用来提高对目标的综合毁伤效应(活性破片、活性药型罩)和材料的综合防护性能[2](冲击反应增韧防护材料),具有很好的应用前景。MESMs的冲击响应力学特性是MESMs设计和应用的基础,亟需对MESMs冲击压缩特性给予准确描述。
在MESMs动态力学性能及冲击物态方程实验研究方面,L.Ferranti等[3-4]利用逆向泰勒杆研究了Al/Fe2O3/epoxy在不同撞击速度下的动态变形行为,获取了试件撞击过程中的变形参数,J.L.Jordan等[5-7]利用轻气炮、爆炸驱动飞片技术获取了Al/Fe2O3/epoxy在2~23GPa压力范围内的冲击 Hugoniot数据,并拟合得到了相关物态方程参数。D.E.Eakins等[8-9]获取了不同密实度条件下Al/Ni冲击压缩实验数据;Xu Xiao[10]利用飞片冲击实验研究了不同加工工艺Ni/Ti的冲击响应特性;徐松林和阳世清等[11-14]利用万能试验机、改进的摆锤冲击试验机和分离式霍普金森压杆研究了PTFE/Al在应变率10-3~103s-1范围内的压缩应力应变关系,并获取了其本构参数。以上实验研究为MESMs冲击压缩行为理论计算提供了实验基础。理论计算方面,张先锋等[15]对MESMs冲击反应过程进行了理论计算,建立了MESMs冲击诱发化学反应释能效率模型,该模型在计算MESMs冲击Hugoniot时采用质量平均法对问题进行简化。综上所述,针对MESMs的研究较少涉及物态方程的理论研究,为了从理论上更加精确地描述MESMs冲击反应机理,有必要对MESMs冲击物态方程进行理论计算。
本文中,拟基于零温混合物冷能叠加原理、Wu-Jing模型,由热力学关系得出具有一定孔隙率的多功能含能结构材料的冲击物态方程。并以W/Cu、Al/Ni、Ni/Ti等典型惰性及含能结构材料为例,计算冲击物态方程,结果显示计算结果与实验结果吻合较好,说明该模型能够较好地描述MESMs冲击物态方程。
1 基于冷能叠加原理的密实混合物冲击压缩特性理论计算
1.1 材料冲击压缩特性理论模型
在流体模型和谐振子模型近似下,忽略自由电子项的影响,可由Grüneisen物态方程和Rankin-Hugoniot能量方程得出固体物态方程计算模型[16]
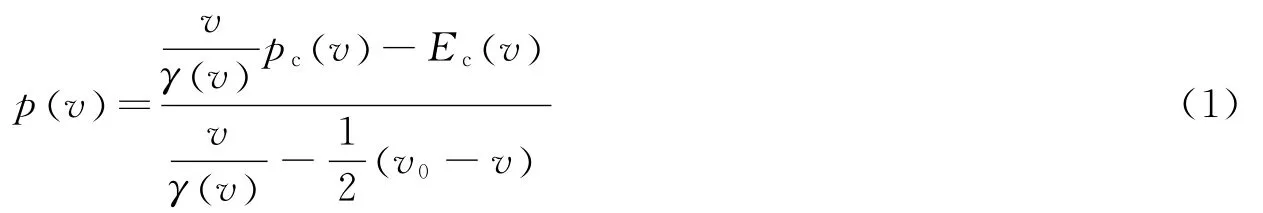
式中:p和v分别为材料的压强和比容,v0为初始比容,pc(v)和Ec(v)表示冷压和冷能,γ(v)为Grüneisen系数。
1.2 混合物材料冷能叠加原理
求解混合物的物态方程时,为了避免温度带来的影响,采用冷能叠加原理计算混合物的冷压线,进一步计算混合物的Hugoniot曲线。
1.2.1 各组分的冷压线计算方法
金属的冷能和冷压通常用Born-Meyer势来描述[17],其表达式为
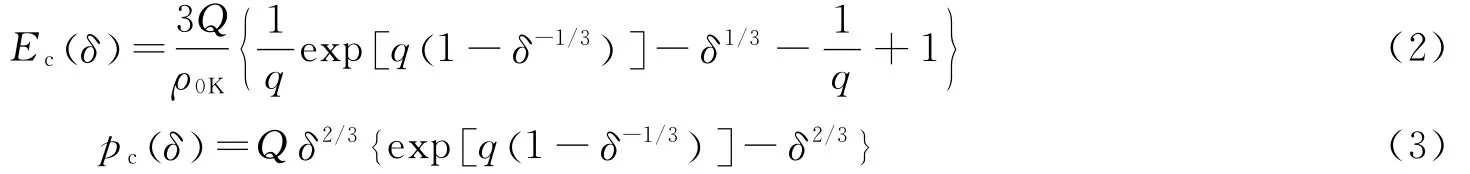
式中:δ=ρ/ρ0K=v0K/v为温度为0K时的压缩度,v0K和ρ0K分别是温度为0K时的比容和密度,Q和q为材料常数,ρ为材料密度。
对于 Grüneisen系数,γ(v)可由Dugdale-MacDonald公式来描述[17]

把方程(3)带入方程(4)中,γ(v)可简化为

式中:材料参数Q和q可由胡金彪等[18]给出的解析方法求出

式中:c0和λ0为温度为0K时的体积声速和材料常数。实际情况下,冲击压缩测量是在室温下进行的,因此必须对室温条件下的体积声速c′0和材料常数λ′进行温度修正,计算公式如下
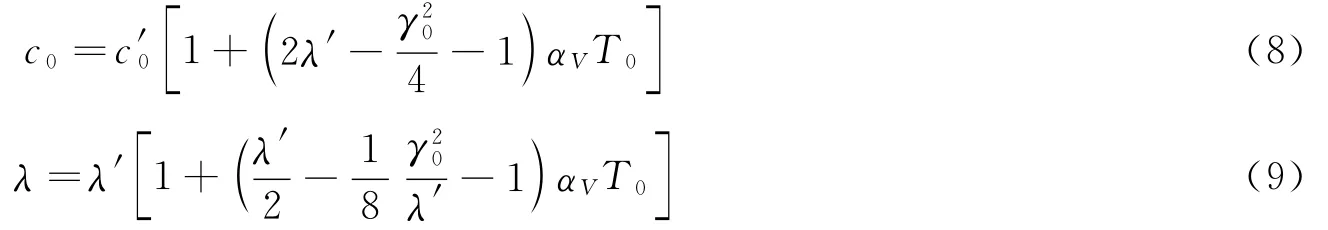
式中:αV为体积膨胀系数,γ0为温度0K时的Grüneisen系数,T0为室温,取298K。
1.2.2 混合物的冷压线计算
材料比容v、内能E由叠加原理得到

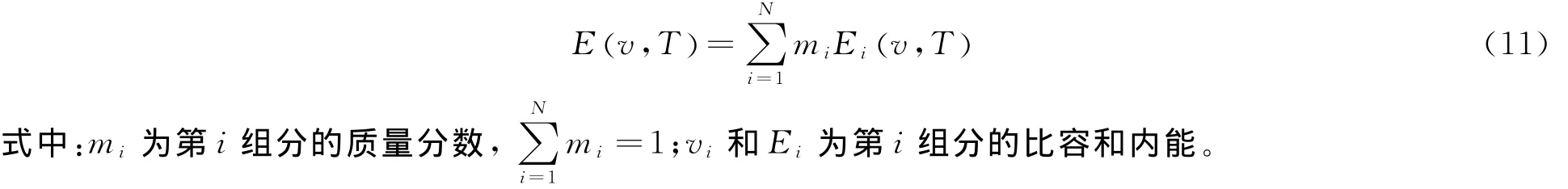
在计算混合物的冲击物态方程时,假设混合物各组分具有相同的粒子速度和压强[19]。通过各组分的Ec-v关系可以得到混合物的冷能值Ec,然后由热力学关系pc=-dEc/dv求得混合物的冷压值。再由Ec-v和pc-v关系根据最小二乘法拟合得到混合物对应的材料参数Q和q。然后根据方程(6)求出Grüneisen系数γ(v),进一步由方程(1)求出密实态混合物的物态方程。
2 疏松材料冲击响应的Wu-Jing模型
疏松材料的物态方程一般是以相应的密实材料的物态方程为基础建立起来的。本文中运用吴强、经福谦基于等压路径提出的Wu-Jing模型[20-21]来描述疏松材料的物态方程。密实材料和疏松材料的物态方程表示如下

式中:vH、v′H、vc、v′c、H、H′、Hc和H′c分别代表密实材料和疏松材料的比容、零温比容、比焓和零温比焓,R为物质参数。
由比焓的定义得

式中E0、E00、v0和v00分别代表密实材料和疏松材料初始比内能和初始比容,取m=v00/v0表示材料的初始密实度。根据吴强、经福谦的假设,在等压条件下,对于同质材料,无论其初始条件为疏松态或密实态,参数R的取值是相等的。所以沿等压路径联立方程(12)~(17)可得
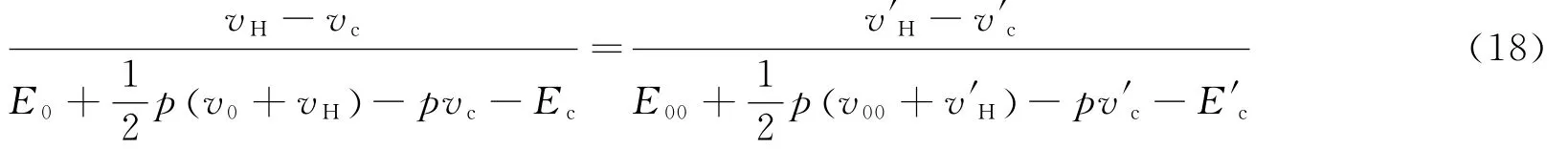
在利用方程(18)求解疏松材料的物态方程之前,必须先求解零温比容v′c和零温比内能E′c。对于同种混合物的疏松态和密实态,当二者所处的温度和压强相等的时候,可以假设二者的比内能是相等的[22],即忽略了孔穴表面的能量,令Ec=E′c。用Born-Meyer势来描述密实材料的零温等温线
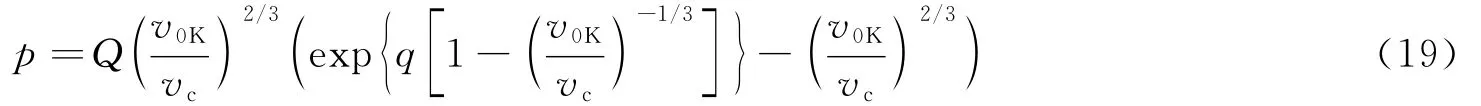
由方程(19)可以求得密实材料的零温比容vc。参数αc表示疏松材料零温时的孔隙度,其表达式为

在强冲击载荷作用下,疏松材料孔隙度αc的变化可用Carroll-Holt’s模型[23]来描述

式中:α0为初始状态下的孔隙度,α0=v00/v0。Y为密实材料的强度极限,pcrit为多孔材料的弹性极限,其解为

3 计算结果及其分析
为进一步验证本模型的有效性,对典型颗粒金属材料(W/Cu合金)和典型MESMs(Al/Ni、Ni/Ti和Al/Fe2O3/epoxy)的冲击物态方程进行了计算,并与已有实验结果进行了对比。计算所需要的材料参数如表1所示。
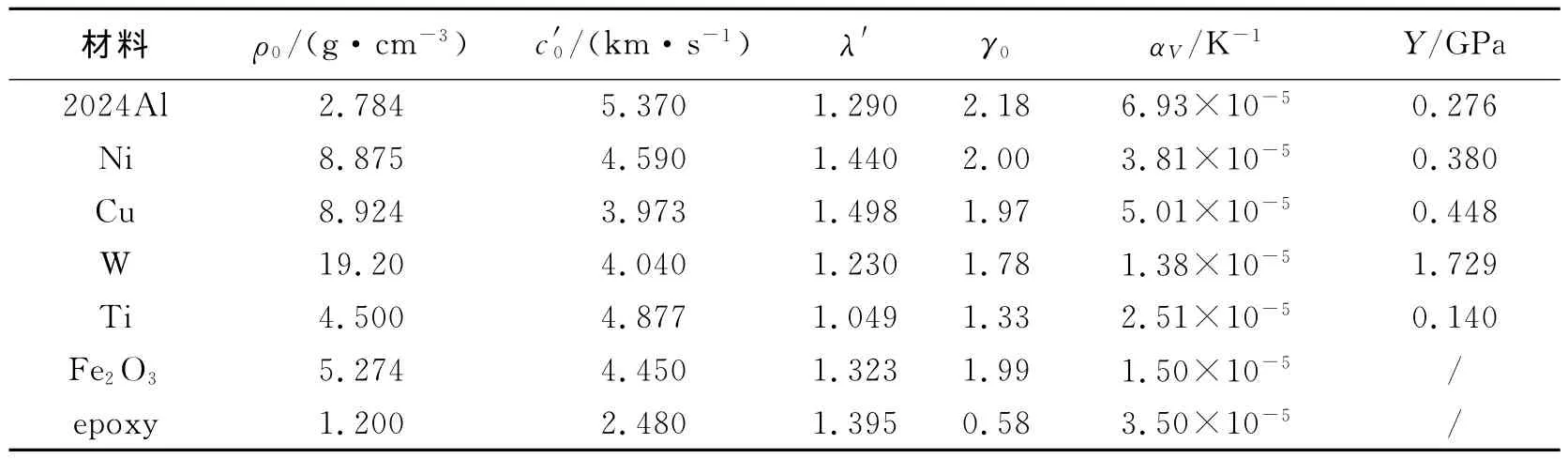
表1 材料的计算参数[16]Table1 The material parameters related to the calculation
首先对各组分的材料参数进行修正,由方程(6)~(7)求得各组分材料的材料参数Q、q,并求出各组分的冷能值Ec;其次由冷能叠加原理求得混合物的冷能值,进一步求出混合物的冷压值,最后根据冷能、冷压值拟合得到混合物的材料参数Q、q。混合物的材料参数计算结果如表2所示。
计算得到混合物的材料参数Q、q后,就可以由式(2)~(3)和式(5)求得混合物的冷能值Ec、冷压值pc和Grüneisen系数γ(v)。然后利用方程(1)求得混合物的物态方程,进一步利用方程(18)求得不同密实度材料的物态方程。

表2 混合物材料参数的计算结果Table2 The calculated materials parameters for mixtures
3.1 颗粒金属材料物态方程计算
图1为颗粒金属材料W/Cu(55/45)的Hugoniot关系的计算值和实验值的对比。从图中可以看出,颗粒金属材料的Hugoniot关系计算值和实验值吻合相当好,都在误差允许范围内。说明本文中建立的模型能够准确地计算出疏松态混合物的冲击物态方程,精确地描绘疏松态混合物的冲击响应行为,图中up、us分别为粒子速度和冲击波速度。
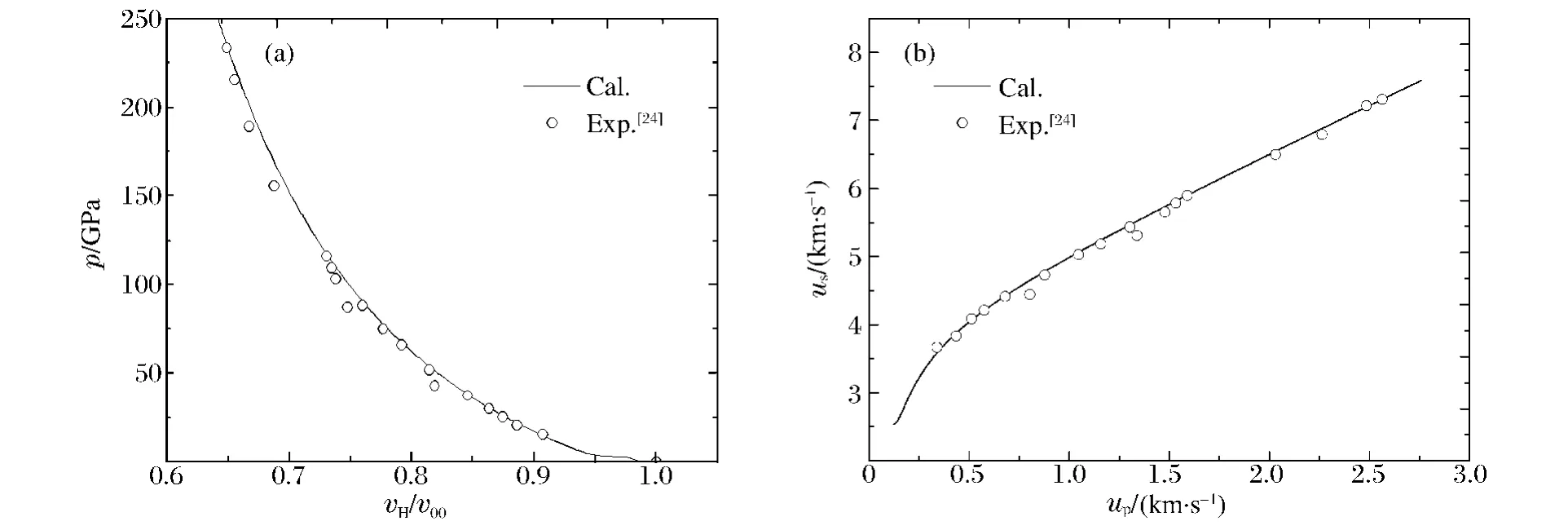
图1 W/Cu(55/45)混合物冲击压缩数据计算结果和实验值对比Fig.1 The calculated and experimental Hugoniots for W/Cu(55/45)mixtures
3.2 MESMs冲击压缩过程计算结果
由于Al/Ni合金体系各种化合物间的化学反应所释放的能量存在巨大的差异,因此Al/Ni作为一种典型的MESMs得到了广泛的研究。图2~3分别为m=45%、60%的Al/Ni的冲击压缩数据计算值与实验值的对比。混合物由等体积的Al、Ni混合而成。
由图2可以看出:(1)随着输入压力p增大,粒子速度up的值也越来越大。当压力p低于3.5 GPa时,计算值与实验数据吻合很好,当压力大于3.5GPa时,混合物开始了化学反应,生成了新的物质,计算数据与实验值有一定差异。(2)从图2(b)中可以看出,up-us近似为线性关系,当混合物没有发生反应时计算值与实验值吻合较好,发生反应后计算值低于实验值。
图3为Al/Ni(m=60%)的冲击压缩曲线,图中的实验数据显示均未发生化学反应[9],从图中看出一些数据点与计算值吻合很好,数据点(0414、0412、0428、0504、0407)误差较大,这是由于实验点输入压力值没有测到,图中所引用的数值由文献[9]根据阻抗匹配关系计算得到,计算过程中无疑增加了许多不确定因素。

图2 Al/Ni(m=45%)冲击压缩曲线计算结果与实验值对比Fig.2 The calculated and experimental Hugoniots for Al/Ni(m=45%)
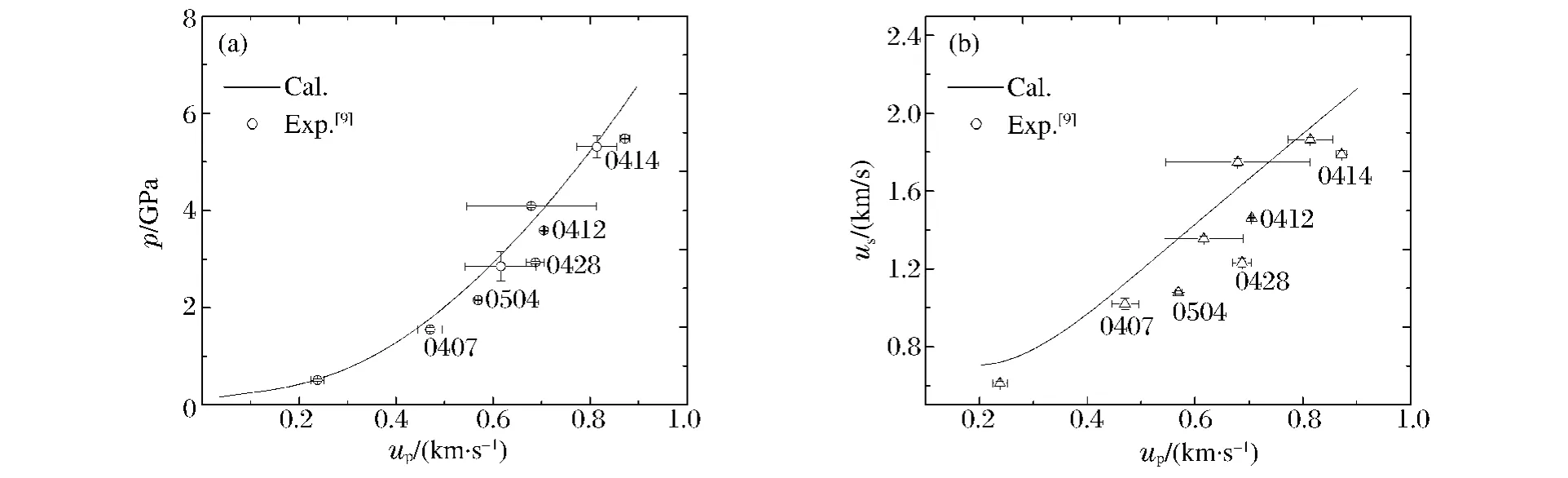
图3 Al/Ni(m=60%)冲击压缩曲线计算结果与实验值对比Fig.3 The calculated and experimental Hugoniots for Al/Ni(m=60%)

图4 Ni/Ti冲击压缩曲线计算结果与实验值对比Fig.4 The calculated and experimental Hugoniots for Ni/Ti
图4和表3为Ni/Ti冲击波速度计算值与实验值的对比,u*s为本文模型的计算结果。混合物中Ni、Ti按等摩尔质量采用混合和球磨2种工艺加工而成。其中球磨工艺会使组分Ni、Ti之间形成更加紧密的混合物,大大减少化学反应所释放的能量。球磨时间越长,试件反应放出的能量越少,体积膨胀量越小,实验点就越接近未考虑化学反应的混合物冲击压缩的计算曲线。从图中可以看出,球磨的试件正好吻合这种情况。对于直接混合的试件,未反应的数据点(0109)与计算结果吻合较好,反应的数据点(0104、0105)随着压力的增加逐步偏离计算曲线。

表3 Ni/Ti冲击波速度计算值与实验值[10]对比Table3 The calculated and experimental Hugoniots for Ni/Ti
3.3 多组分MESMs冲击压缩特性计算结果
多组分MESMs一般由金属混合物加上聚合物混合而成,典型多组分 MESMs如Al/Fe2O3/epoxy。从图5(a)中冲击p-up曲线可以看出,在较低压力段(轻气炮加载),计算值与实验点吻合较好,在爆炸加载的中高压力段,计算值与实验点存在一定误差。us-up曲线,计算值与实验值存在较大差异。造成误差的原因在于:首先,实验当中存在着诸多不确定因素[5-6];其次,对Al/epoxy混合物的中尺度数值模拟[25]显示,在冲击波传播的时间尺度内混合物的各组分之间没有达到压力和温度平衡,计算结果会高于实验结果;第三,THV500冲击实验结果显示:由于THV500的分解,Hugoniot参数计算结果与实验结果也存在类似差异[26]。从图5可以看出,本文计算结果可以大致预测多组分MESMs冲击响应趋势,误差原因有待进一步研究。

图5 Al/Fe2O3/epoxy(12.63/37.37/50.00)冲击压缩曲线计算结果与实验值对比Fig.5 The calculated and experimental Hugoniots for Al/Fe2O3/epoxy(12.63/37.37/50.00)
综上所述,从颗粒金属材料物态方程的计算值和实验值的对比,可以看出本文中建立的模型能够准确地计算出疏松态混合物的冲击物态方程。对于MESMs,冲击压缩数据的计算结果与未发生反应情况下的实验结果吻合较好,与发生反应情况下的实验结果存在一定差异。要研究MESMs发生反应情况下的冲击压缩数据,需要加入化学反应动力学模型来表征MESMs的化学反应情况。从整体上说,该模型能够准确计算出MESMs在未发生化学反应情况下的物态方程。
4 结 论
(1)基于冷能叠加原理和Wu-Jing方程,由热力学关系建立了求解疏松态混合物物态方程的理论模型,并以 W/Cu、Al/Ni、Ni/Ti、Al/Fe2O3/epoxy为例,计算了典型颗粒金属材料、典型 MESMs的冲击物态方程。结果显示,该模型能够很好地描述疏松态混合物的冲击压缩行为,对于未反应MESMs,冲击物态方程的计算能够给出令人满意的结果。(2)对于发生化学反应的MESMs冲击压缩数据的计算,需要进一步加入化学反应动力学理论来考虑生成物对冲击响应情况的影响。(3)对于金属聚合物配方的MESMs,研究其冲击响应行为需要从细观入手,考虑聚合物对混合物冲击响应方式的影响,利用细观与宏观相结合的方法展开研究工作。
下一步的工作重点是根据化学反应动力学理论,加入化学反应模型建立考虑化学反应的MESMs冲击物态方程的理论计算模型。
[1]Committee on Advanced Energetic Materials and Manufacturing Technologies of National Research Council.Advanced Energetic Materials[M].Washington:The National Academies Press,2004.
[2]张先锋,赵晓宁.多功能含能结构材料研究进展[J].含能材料,2009,17(6):731-739.Zhang Xian-feng,Zhao Xiao-ning.Review on multifunctional energetic structural materials[J].Chinese Journal of Energetic Materials,2009,17(6):731-739.
[3]Ferranti L,Thadhani N N.Dynamic mechanical behavior characterization of epoxy-cast Al+ Fe2O3thermite mixture composites[J].Metallurgical and Materials Transactions:A,2007,38(1):2697-2715.
[4]Ferranti L,Thadhani N N,House J W.Dynamic mechanical behavior characterization of epoxy-cast Al+Fe2O3mixtures[J].AIP Conference Proceedings,2006,845(1):805-808.
[5]Jordan J L,Dick R D,Ferranti L.Equation of state of aluminum-iron oxide-epoxy composite:Modeling and experiment[J].AIP Conference Proceedings,2005,845(1):157-160.
[6]Jordan J L,Ferranti L,Austin R.Equation of state of aluminum-iron oxide-epoxy composite[J].Journal of Applied Physics,2007,101(9):093520-093528.
[7]Jordan J L,Dattelbaum D,Ferranti L.Shock equation of state of single constituent and multi-constituent epoxybased particulate composites[J].AIP Conference Proceedings,2009,1195(1):1253-1256.
[8]Eakins D E,Thadhani N N.Mechanistic aspects of shock-induced reactions in Ni-Al powder mixtures[J].AIP Conference Proceedings,2007,955(1):1025-1028.
[9]Eakins D E.Role of heterogeneity in the chemical and mechanical shock-response of nickel and aluminium powder mixtures[D].Atlanta:Georgia Institute of Technology,2003.
[10]Xu Xiao,Thadhani N N.Investigation of shock-induced reaction behaviour of as-blended and ball-milled Ni-Ti powder mixtures using time-resolved stress measurements[J].Journal of Applied Physics,2004,96(4):2000-2009.
[11]徐松林,阳世清,徐文涛,等.PTFE/Al反应材料的力学性能研究[J].高压物理学报,2009,23(5):384-388.Xu Song-lin,Yang Shi-qing,Xu Wen-tao,et al.Research on the mechanical performance of PTFE/Al reactive materials[J].Chinese Journal of High Pressure Physics,2009,23(5):384-388.
[12]阳世清,徐松林,张彤.PTFE/Al反应材料制备工艺及性能[J].国防科技大学学报,2008,30(6):39-42.Yang Shi-qing,Xu Song-lin,Zhang Tong.Preparation and performance of PTFE/Al reactive materials[J].Journal of National University of Defense Technology,2008,30(6):39-42.
[13]徐松林,阳世清,李俊玲,等.PTFE/Al含能复合材料的压缩行为研究[J].力学学报,2009,41(5):708-712.Xu Song-lin,Yang Shi-qing,Li Jun-ling,et al.The study on the compressive behaviour of PTFE/Al energetic composite[J].Chinese Journal of Theoretical and Applied Mechanics,2009,41(5):708-712.
[14]徐松林,阳世清,张炜,等.PTFE/Al含能复合物的本构关系[J].爆炸与冲击,2010,30(4):439-444.Xu Song-lin,Yang Shi-qing,Zhang Wei,et al.A constitutive relation for a pressed PTFE/Al energetic composite material[J].Explosion and Shock Waves,2010,30(4):439-444.
[15]张先锋,赵晓宁,乔良.反应金属冲击反应过程的理论分析[J].爆炸与冲击,2010,30(2):145-151.Zhang Xian-feng,Zhao Xiao-ning,Qiao Liang.Theory analysis on shock-induced chemical reaction of reactive metal[J].Explosive and Shock Waves,2010,30(2):145-151.
[16]Zhang X F,Qiao L,Shi A S,et al.A cold energy mixture theory for the equation of state in solid and porous metal mixtures[J].Journal of Applied Physics,2011,110(1):013506-013515.
[17]汤文辉,张若棋.物态方程理论计算概论[M].北京:高等教育出版社,2008.
[18]胡金彪,经福谦.用冲击压缩数据计算物质结合能的一个简便解析方法[J].高压物理学报,1990,4(3):175-186.Hu Jin-biao,Jing Fu-qian.A simplified analytical method for calculations of equation-of-state of materials from shock compression data[J].Chinese Journal of High Pressure Physics,1990,4(3):175-186.
[19]Barry R K,Thad V J.A Hugoniot theory for solid and powder mixtures[J].Journal of Applied Physics,1991,69(2):710-716.
[20]Wu Q,Jing F Q.Unified thermodynamic equation-of-state for porous materials in a wide pressure range[J].Journal of Applied Physics,1995,67(1):49-51.
[21]Wu Q,Jing F Q.Thermodynamic equation of state and application to Hugoniot predictions for porous materials[J].Journal of Applied Physics,1996,80(8):4343-4349.
[22]Herrmann W.Constitutive equation for the dynamic compaction of ductile porous materials[J].Journal of Applied Physics,1969,40(6):2490-2499.
[23]Carroll M M,Holt A C.Static and dynamic pore-collapse relations for ductile porous materials[J].Journal of Applied Physics,1972,43(4):1626-1636.
[24]Marsh S P,LASL shock Hugoniot data[M].Berkeley,CA:University of California Press,1980.
[25]Deas D,Millett J C F,Bourne N K,et al.The shock Hugoniot of two alumina-epoxy composites[J].AIP Conference Proceedings,2004,706(1):693-696.
[26]Dattelbaum D M,Sheffield S A,Stahl D,et al.Equation of state and high pressure properties of a fluorinated terpolymer:THV500[J].Journal of Applied Physics,2008,104(11):113525-113535.
