中国首台准环对称仿星器中离子温度梯度模的模拟研究*

黄捷 李沫杉 覃程 王先驱

(西南交通大学物理科学与技术学院,成都 610031)

中国首台准环对称仿星器(CFQS)是目前世界上唯一在建的准环对称仿星器.本文利用回旋弗拉索夫代码GKV 开展了CFQS 中离子温度梯度模(ITG)的模拟研究.在静电绝热条件下,模拟的结果给出了CFQS 中纯的ITG 与密度梯度和温度梯度间的依赖关系.ITG 的激发存在温度梯度阈值,此温度梯度阈值受到密度梯度的影响.ITG 的增长率不仅与密度梯度的绝对值相关,还取决于密度梯度的正负,负密度梯度对ITG 具有强的抑制作用.非绝热的模拟结果表明,捕获电子对ITG 具有去稳作用,电子温度梯度也对ITG 具有去稳作用.当考虑电磁条件时,有限的等离子体比压会抑制ITG,导致ITG 向阿尔芬离子温度梯度模/动理学气球模(AITG/KBM)的转化.当密度和温度梯度都较大时,KBM 的最大增长率与密度梯度和温度梯度近似成线性关系.

1 引言

在磁约束聚变装置中,湍流输运导致的等离子体粒子和能量损失严重影响等离子体的约束性能.在托卡马克装置中,湍流输运是最主要的等离子体输运损失方式.但在仿星器中,除湍流输运外,新经典输运也是一种主要的等离子体输运损失方式[1].由于存在大的新经典输运,长期以来仿星器的约束性能都不如托卡马克.仿星器中大的新经典输运是由于仿星器中大的磁场波纹度导致的[2].因此,可以通过优化仿星器的磁场位形,降低其磁场波纹度,进而提高对等离子的约束性能.仿星器磁场位形的优化主要有三种方式: 准螺旋对称优化(如美国的HSX 装置)、准力线优化(如德国的W7-X 装置)和准环对称优化[3-5].利用前两种优化方式优化的仿星器都已建成并运行,但在这两类仿星器上的研究结果表明,以这两种优化方式优化的仿星器仍然具有大的新经典输运[1].理论研究表明,采用准环对称优化的仿星器具有与托卡马克相当的新经典输运水平,这能大大地降低仿星器的新经典输运损失[6].准环对称优化的仿星器克服了传统仿星器新经典输运大的缺点,同时保留了仿星器无等离子体电流的优点,是一种比较理想的约束等离子体的磁场位形.

到目前为止,国际上尚无建成的基于准环对称优化的仿星器装置.美国曾经计划建造一台准环对称仿星器装置NCSX[7],日本也曾设计过一台准环对称仿星器装置CHS-qa[8].最近,中国西南交通大学联合日本核融合科学研究所共同设计了一台准环对称仿星器—中国首台准环对称仿星器(CFQS),并已开始装置的建造[6,9-12].CFQS 是目前世界上唯一在建的准环对称仿星器装置.

虽然理论研究表明CFQS 的新经典输运水平远低于现有的仿星器,可以与托卡马克相比拟[6],但CFQS 对等离子体的整体约束性能不仅取决于其新经典输运水平,还取决于其湍流输运水平.因此,要从理论上验证CFQS 磁场位形的先进性,还需要对其开展湍流输运的模拟研究.等离子体中的湍流输运是由等离子体中的静电和电磁微观不稳定性驱动的,如离子温度梯度模(ITG)、捕获电子模(TEM)等[13].

本文利用回旋动理学弗拉索夫代码GKV 开展CFQS 中离子尺度的微观不稳定性的研究,给出CFQS 上ITG 和阿尔芬离子温度梯度模/动理学气球模(AITG/KBM)的特征.

2 物理模型

本文利用回旋弗拉索夫代码GKV 开展CFQS上静电和电磁ITG 的模拟研究.GKV 代码是基于δf的回旋动理学模型,通过求解随时间演化的电子或离子扰动分布函数 δfs、静电势ϕ和失势的平行分量A//来开展等离子体物理的研究,其中,s=i 和s=e 分别是离子和电子的扰动分布函数[14,15].GKV 代码的核心方程是在五维相空间里扰动分布函数的电磁回旋动理学方程[16,17],方程的傅里叶展开形式如下:

在GKV 中采用通量管坐标系 (x,y,z)[18],其中,x=a(ρ-ρ0),y=aρ0q(ρ0)-1[q(ρ)θ-ζ],z=θ.这里a为小半径,ρ=,ψ为环向磁通,q(ρ0)为ρ=ρ0处的安全因子,θ为极向角.在后面的模拟中,在环向角ζ=0°、归一化小半径ρ=0.5 处取一个通量管作为模拟区域.CFQS 的大半径为1 m,纵横比为4,其准环对称磁场位形的环向周期数为2.

3 数值模拟

离子温度梯度模是由离子温度梯度驱动的一种微观不稳定性,除了离子温度梯度外,等离子体的密度梯度、捕获电子、等离子体比压等都对ITG有影响.本文主要考虑在绝热和非绝热情况下,温度梯度和密度梯度对ITG 的影响.在绝热情况下,等离子体的微观不稳定性是纯的ITG 模,这样可以在CFQS 仿星器上研究纯的ITG 模与温度梯度和密度梯度间的依赖关系.

3.1 静电模拟结果

首先,考虑静电绝热条件下CFQS 中的ITG 模.在这种条件下,可以研究纯的ITG 与等离子体参数间的依赖关系,为了解CFQS 中ITG 模的激发和稳定条件提供理论依据.图1 给出了静电绝热条件下ITG 模的波数谱.图1 中的γ为增长率;ky为波数;ρi为离子回旋半径;R0为装置大半径;Ln和LT分别为密度和温度梯度标长,其定义为Ln=-(d lnn/dx)-1,LT=-(d lnT/dx)-1,其中n和T分别为等离子体密度和温度.由图1 可以看出,随着温度梯度增大,ITG 的波数谱变得越来越宽,增长率越来越大,高波数的ITG 变得更不稳定.而随着密度梯度的增大,ITG 的波数谱逐渐展宽,最大增长率对应的波数往高波数区移动.总体来看,随密度梯度的增大,ITG 增长率则先增大再减小.由图1 还可以看出,ITG 的激发存在一个温度梯度阈值,只有当温度梯度大于该阈值时,ITG 才能被激发.这个温度梯度阈值的大小强烈依赖于密度梯度.鉴于实验上可能出现中空的密度剖面,在CFQS 位形下开展了负密度梯度对ITG 影响的研究.由图1(a)和图1(b)可以看出,虽然R0/Ln=-2和R0/Ln=2 这两个密度梯度的绝对值相同,但对应ITG 的增长率却明显不同,负密度梯度对ITG具有抑制作用.这与托卡马克上的结果相同[19,20].因此,ITG 的增长率不仅与密度梯度的绝对值相关,还取决于密度梯度值的正负.图2 给出了图1条件中ITG 的频率.ITG 的传播方向为离子抗磁漂移方向,在本文模型中,以电子的抗磁漂移方向为正方向,因此ITG 的频率为负值.由图2 可以看出,温度梯度对ITG 频率的影响不大,但密度梯度对ITG 频率的影响很大.ITG 的频率随密度梯度数值的增大而减小,这跟增长率与密度梯度之间的依赖关系不同,ITG 的频率只与密度梯度的数值大小有关,密度梯度的数值越大,ITG 的频率越小.在托卡马克中也给出了相同的结果[20].结合图1,对于同一个密度梯度,ITG 越不稳定,其频率越大.对于固定的密度梯度和温度梯度,频率与波数近似成线性关系,即ITG 的相速度近似为常数.这与托卡马克和仿星器(如NCSX)中的结果一致[21,22].ITG 的相速度与温度梯度成正比,与密度梯度成反比.当密度梯度大时,如图2 中的R0/Ln=8,波数kyρi≤1 时,ITG 的频率趋近于0.

图1 不同密度梯度和温度梯度下绝热ITG 的增长率波数谱 (a) R0/Ln=-2;(b) R0/Ln=2;(c)R0/Ln=8Fig.1.Growth rate spectra of ITG for different density gradients and temperature gradients: (a) R0/Ln=-2;(b) R0/Ln=2;(c) R0/Ln=8.

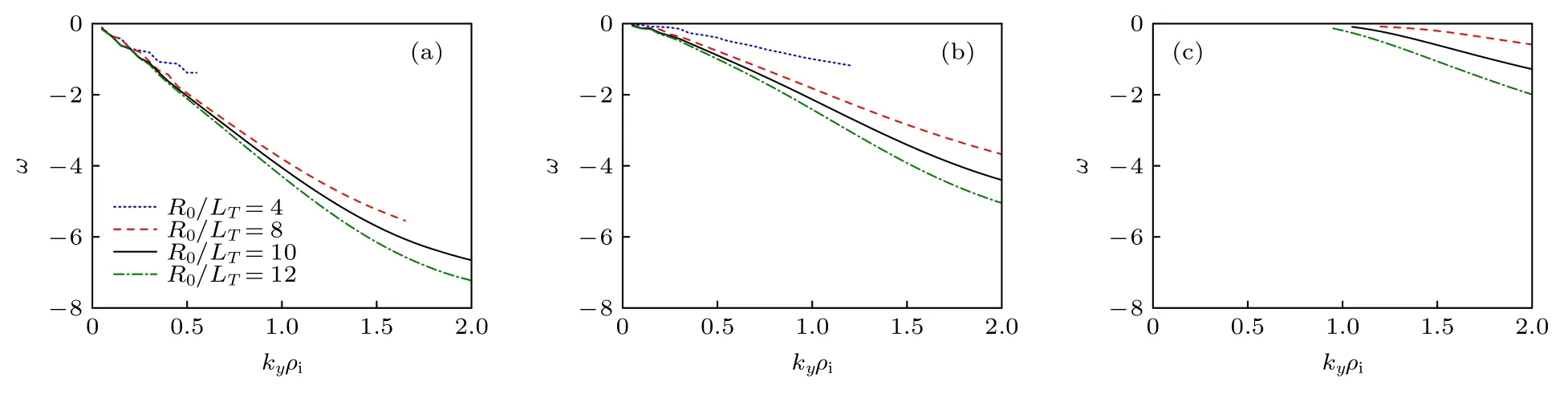
图2 不同密度梯度和温度梯度下绝热ITG 的频率波数谱 (a) R0/Ln=-2;(b) R0/Ln=2;(c)R0/Ln=8Fig.2.Real frequency spectra of ITG for different density gradients and temperature gradients: (a) R0/Ln=-2;(b) R0/Ln=2 ;(c) R0/Ln=8 .

图3 给出了CFQS 中绝热ITG 的最大增长率与密度梯度和温度梯度间的关系.由图3 可以看出,当温度梯度最大、密度梯度在R0/Ln～3 附近时,ITG 最不稳定.随着密度梯度的增大或者减小,ITG 的增长率都减小.这意味着有限的密度梯度既可以驱动ITG(当密度梯度较小时),也可以抑制ITG(当密度梯度大时或者密度梯度为负值时).由图3 可以容易地看出,ITG 的激发存在一个温度梯度阈值,该阈值强烈受到密度梯度的影响.对于CFQS,激发ITG 的温度梯度阈值R0/LTc＞3.对于ITG,ηi=Ln/LT是一个重要的参量.当密度梯度不变,温度梯度增大(LT减小)时,ηi随温度梯度增大而增大,从图3 可以看出,ITG 的增长率也逐渐增大.而若温度梯度不变,密度梯度减小(Ln增大),则ηi随密度梯度减小而增大.从图3 可以看出,此时ITG 的增长率随ηi增大不是单调变化的,而是先增大再减小.这与托卡马克和其他仿星器(如NCSX 和LHD)中的结果相同[19,20,22-25].文献[20]给出了托卡马克等离子体中若固定密度梯度,则ITG 的增长率随着温度梯度增大(或ηi增大)而增大,此外也给出了ITG 增长率随密度梯度和温度梯度变化的等高线图,这都与CFQS 中的结果是一致的.在仿星器中,如NCSX 上,也给出了当固定温度梯度,ITG 的增长率随密度梯度减小(或ηi增大)先增大再减小的结果[22].

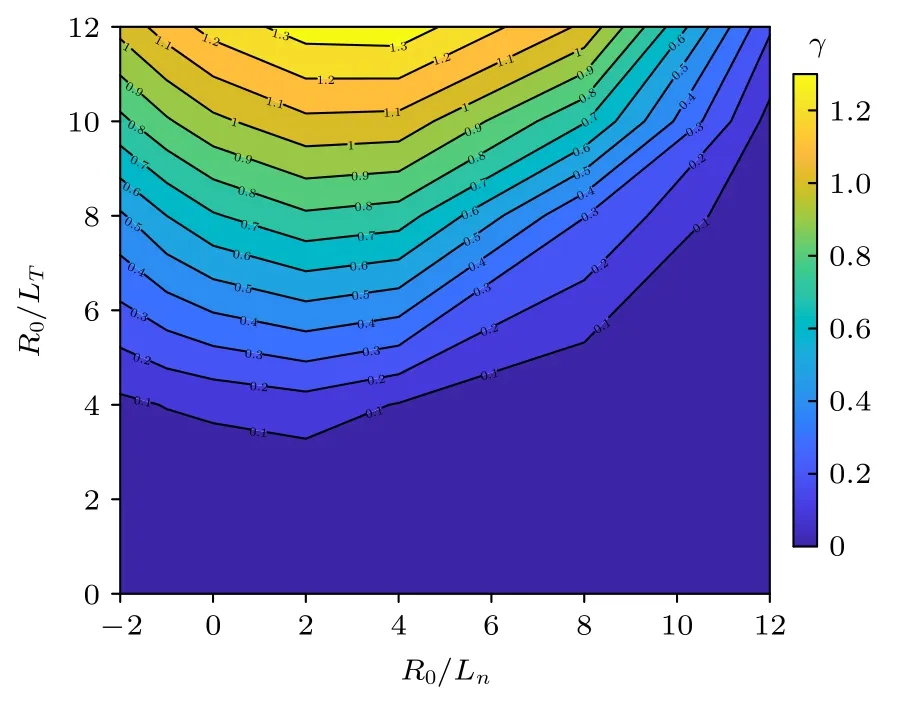
图3 绝热ITG 的最大增长率与密度梯度和温度梯度的关系Fig.3.Relationship of the maximum growth rate of adiabatic ITG to R0/Ln and R0/LT.

若在模型中考虑动理学电子效应,则可以研究存在捕获电子时ITG 的激发和稳定条件,并研究捕获电子对TIG 的影响.但是,考虑了捕获电子效应后,可能会激发另一种微观不稳定性—捕获电子模(TEM).通常,TEM 的空间尺度比ITG 小,而本文研究低波数区的微观不稳定性,因此微观不稳定性以ITG 为主[26].但当ITG 的驱动比较小时,可能出现ITG 和TEM 共同存在的情况,也可能出现耦合的TE-ITG 模,这个耦合的模在托卡马克和仿星器中都可以出现[27-31].

存在捕获电子效应后,ITG 的增长率和频率波数谱如图4 所示.由前面绝热的结果知,R0/Ln=2 时ITG 最不稳定,故图4 中等离子体的密度梯度取R0/Ln=2 .与图1(b)和图2(b)相比较,发现在考虑捕获电子效应后,ITG 的增长率增大.这意味着捕获电子能使ITG 变得更不稳定,降低了激发ITG 的温度梯度阈值[22,32].捕获电子对ITG 的这种效应不依赖于装置的类型,即与装置是托卡马克还是仿星器没有关系.与绝热的结果一样,ITG的增长率越大,其相速度也越大,且ITG 的相速度对同一密度梯度和温度梯度近似为常数.但考虑了捕获电子后,ITG 的频率和相速度都比绝热的结果小.图5 给出了当考虑捕获电子效应后ITG 最大增长率与密度梯度和温度梯度间的关系.由图5可看出: 在大的温度梯度区间,ITG 最大增长率与密度和温度梯度的关系与绝热的结果(图3)相似,只是增长率的数值更大一些;但在低的温度梯度区,其结果与绝热的结果存在一定的差异,可能的原因是当温度梯度小的时候,无法驱动出具有大增长率的ITG.大的密度梯度一方面可以抑制ITG,另一方面又可以驱动TEM,产生所谓的密度梯度驱动的TEM[27];此外,在该参数区间ITG 和TEM的驱动都不强,有可能形成耦合的TE-ITG 模[28-31].故在该参数区间里ITG 不是主导的不稳定性,此时以耦合的TE-ITG 模或混合的ITG 和TEM 为主.这种耦合的TE-ITG 模或混合的ITG 和TEM在托卡马克和其他位形的仿星器中都能产生[27-31].

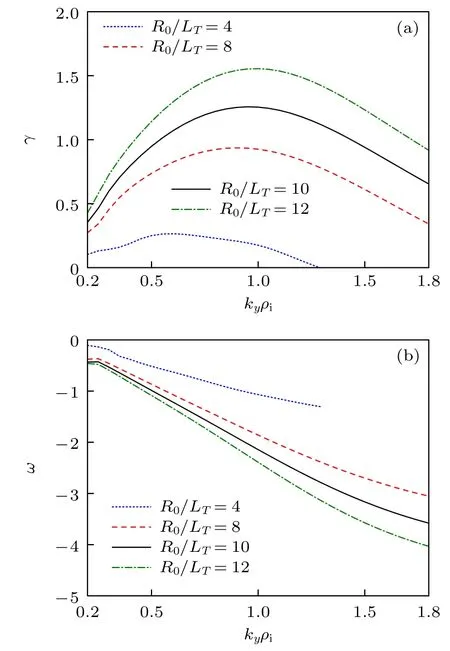
图4 考虑捕获电子效应后ITG 的增长率(a)和频率(b)波数谱,其中 R0/Ln=2,电子温度梯度标长和离子温度梯度标长相等,即Fig.4.Growth rate (a) and real frequency spectra (b) of kinetic ITG for R0/Ln=2 .Here,.

图5 考虑捕获电子效应后ITG/TE-ITG 最大增长率与密度梯度和温度梯度的关系,其中Fig.5.Contour map of the maximum growth rate of kinetic ITG/TE-ITG mode vs.R0/Ln and R0/LT.Here,=.

实际上,在真实的磁约束等离子体中,电子的温度容易受外界电子回旋共振加热(ECRH)的影响.CFQS 未来的加热手段采用的是ECRH,这导致CFQS 等离子体中电子温度梯度和离子温度梯度的不同.在前面的研究中,电子温度梯度和离子温度梯度相等.为研究不相同的电子温度梯度和离子温度梯度对CFQS 中ITG 的影响,以及电子温度梯度如何影响ITG,在下面的模拟中,固定电子的温度梯度为=8 .

图6 给出了R0/Ln=2 时ITG 增长率和频率的波数谱.显然,图6 中=8 的曲线与图4中R0/LT=8 曲线是完全相同的.与图4 相比,当＞8时,ITG 的增长率略有降低,这个降低主要体现在高波数的ITG 上;当＜8 时,ITG的增长率略有增大;而对于ITG 的频率,变化规律则相反.这说明电子温度梯度可以影响ITG,它对ITG 具有一定的去稳作用,特别是对高波数的ITG.在托卡马克中也给出相同的结论[33].图7 给出了当电子温度梯度固定时,ITG 的最大增长率与密度梯度和离子温度梯度间的关系.图7 的结果与绝热的结果(图3)相似,与图5 的结果略有不同.这主要是因为=8 能够驱动大的TEM,故当离子温度梯度小时,不稳定性以TEM 为主;TEM的驱动大,无法形成耦合的TE-ITG 模[29].

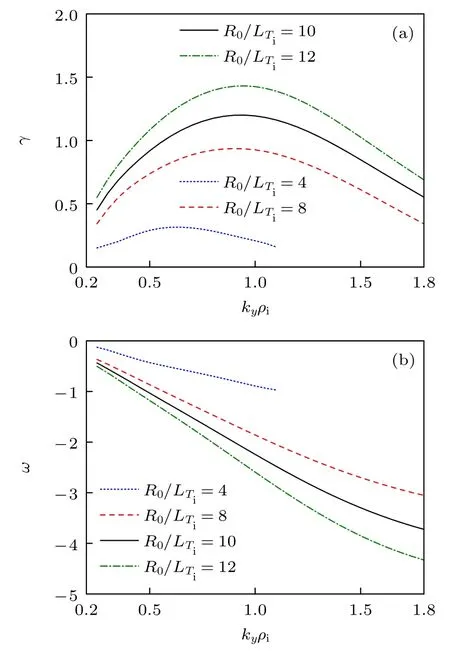
图6 考虑捕获电子效应后ITG 的增长率(a)和频率波数谱(b),其中 R0/Ln=2,=8Fig.6.Growth rate (a) and real frequency spectra (b) of kinetic ITG for R0/Ln=2 and =8.

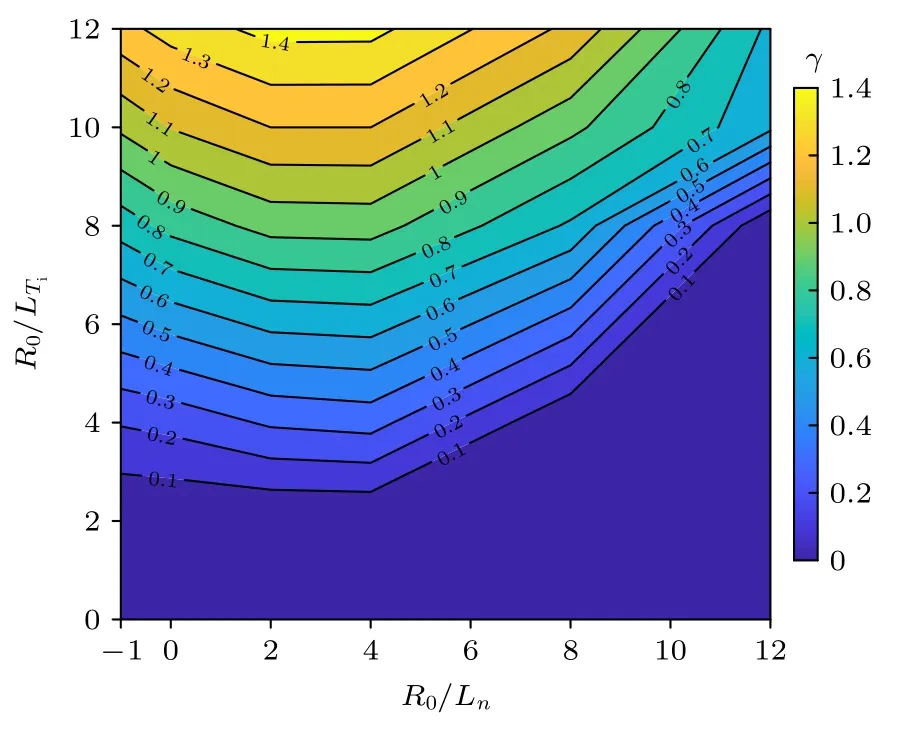
图7 考虑捕获电子效应后ITG 最大增长率与密度梯度和离子温度梯度的关系,其中=8Fig.7.Contour map of the maximum growth rate of kinetic ITG vs.R0/Ln and .Here,=8.

3.2 电磁模拟结果

在前面的模拟中,设定等离子体比压β=0%,即模拟静电条件下ITG 的特征.如果在模型中考虑有限的比压,则可以研究电磁条件下ITG 的特征,并获知在CFQS 中有限比压对ITG 的影响.等离子体的比压定义为等离子体的热压与磁压的比值,即β=µ0nT/B2,其中µ0是真空磁导率,B是磁场.图8 给出了离子尺度(kyρi=1.0)的微观不稳定性的增长率和频率与等离子体比压间的关系.由图8(a)可以看到,增长率在β=0.3% 处有个拐点,在图中用蓝色箭头指出.在拐点左侧,不稳定性为ITG,其增长率随比压的增大而减小,而在拐点右侧,不稳定性为动理学气球模(KBM),其增长率随比压的增大而增大[34-36].离子尺度微观不稳定性的这种特征在托卡马克中同样也是存在的[34,35],只是模拟的条件不同,导致转换点处对应的比压值也不同.其实,KBM 也可以看成是电磁版本的ITG,即AITG[37-39].考虑了电磁条件,β0.3% 是ITG转变为AITG/KBM 的转变点.因此,考虑有限比压效应后,离子尺度的微观不稳定性以AITG/KBM 为主.

图8 当波数 kyρi=1.0 时增长率(a)与频率(b)随比压的变化(其中,R0/Ln=2 ,=8),图(a)中的箭头是从ITG 转变为KBM 的转变点Fig.8.Growth rates (a) and real frequencies (b) vs.β for R0/Ln=2 and =8 at kyρi=1.0 .The arrow is plotted in panel (a) to point the transition point from ITG to KBM.

下面取β=1%,由图8 可知,此时离子尺度的微观不稳定性以AITG/KBM 为主.图9 给出了R0/Ln=2,=8 时KBM 的增长率和频率波数谱.与前面静电的模拟结果不同,电磁条件下,波数小的微观不稳定性具有更大的增长率,增长率随波数近似成单调递减的关系.但从图9 也可以看出,当波数kyρi0.1 时,增长率随着波数减小而减小.在托卡马克和其他位形的仿星器中也有类似的KBM 增长率波数谱[35,40].而频率的大小与静电的结果类似,随着波数的增大而增大,但在电磁条件下,频率与波数不再具有近似线性的关系,即相速度不再近似为常数,而是随着波数的增大而减小.图10 给出了考虑有限比压效应后KBM 的最大增长率与密度梯度和温度梯度间的关系.由于KBM 的驱动源为压强梯度,即大的密度梯度和大的温度梯度都能驱动大的KBM,因此,随着密度梯度和温度梯度的增大,KBM 的增长率也逐渐增大.由图10 可以看出,当密度梯度和温度梯度都较大时(4),KBM 的最大增长率与密度梯度和温度梯度近似成线性关系.与前面静电ITG 的结果不同,负密度梯度对KBM 没有明显的抑制作用.

图9 取 β=1% 时,KBM 的增长率(a)和频率(b)波数谱,其中 R0/Ln=2 ,=8Fig.9.Growth rate (a) and real frequency spectra (b) of KBM for R0/Ln=2 and =8.Here,β=1% .

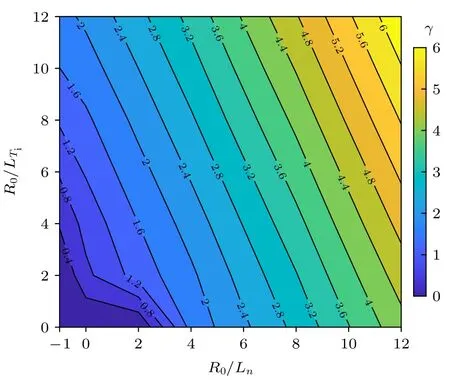
图10 取 β=1% 时,KBM 的最大增长率与密度梯度和离子温度梯度的关系,其中=8Fig.10.Contour map of the maximum growth rate of KBM vs.R0/Ln and .Here,=8 and β=1% .

4 总结

本文研究了CFQS 中静电和电磁ITG,给出了不同等离子体密度梯度和温度梯度条件下的ITG 特征,对CFQS 上离子尺度的微观不稳定性有了一个初步的认识.

在静电绝热条件下,随着温度梯度的增大,ITG 的增长率和频率都增大,ITG 的波数谱越来越宽,高波数的ITG 变得不稳定.ITG 的激发存在一个温度梯度阈值,只有当温度梯度大于该阈值时,才能出现ITG.对于CFQS,其温度梯度阈值＞3.随着密度梯度的增大,ITG 的增长率先增大再减小,而ITG 的频率单调减小.ITG 的增长率不仅与密度梯度的绝对值相关,还取决于密度梯度的正负,负密度梯度对ITG 具有强的抑制作用.而ITG 的频率只与密度梯度的数值大小有关,密度梯度的数值越大,ITG 的频率越小.在CFQS中,当密度梯度R0/Ln≈2.5,温度梯度取最大时,ITG 具有最大的增长率.当固定密度梯度和温度梯度,不同波数的ITG 的相速度近似为常数.ITG的相速度随温度梯度的增大而增大,随密度梯度的增大而减小

在考虑捕获电子效应后,与绝热的结果相比,ITG 的增长率增大,意味着捕获电子对ITG 具有去稳作用,而ITG 的频率略有降低,相速度减小.当温度梯度大时,ITG 的最大增长率与密度梯度和温度梯度的依赖关系同绝热的结果相同.但当温度梯度小时,会出现耦合的TE-ITG 模或者由大的密度梯度驱动的TEM,导致在低温度梯度区以耦合的TE-ITG 模或混合的ITG 和TEM 为主.当固定电子温度梯度=8,可以获知电子温度梯度和离子温度梯度对CFQS 中ITG 的影响.电子温度梯度对ITG 具有一定的去稳作用.由于此时TEM 的驱动较强,无法形成耦合的TE-ITG 模.

当考虑电磁条件时,有限的等离子体比压会抑制ITG,随着等离子体比压的增大,在β～0.3% 时出现了ITG 向AITG/KBM 的转化.此后,随着比压继续增大,KBM 的增长率也增大.KBM 增长率的波数谱与ITG 的不同,KBM 的增长率随着波数近似单调下降.随着密度梯度和离子温度梯度的增大,KBM 的增长率也逐渐增大.当密度和温度梯度都较大时(4),KBM 的最大增长率与密度梯度和温度梯度近似成线性关系.

CFQS 仿星器是三维平衡,不同环向位置的磁场位形不同[11].取不同环向位置构建的通量管的磁场位形不同,这对ITG 的模拟结果会有影响.在本文中,在环向角为0°处取一个通量管作为模拟区域,在此区域中ITG 的增长率最大,在半个环向周期内随着环向角增长,ITG 的增长率逐渐减小.