DSPH方法的有效性验证及应用*
2013-09-19张岳青
闫 蕊,徐 绯,张岳青
(1.西北工业大学航空学院,陕西 西安 710072;2.北京理工大学爆炸科学与技术国家重点实验室,北京 100081)
光滑粒子流体动力学(smoothed particle hydrodynamics,SPH)方法是一种典型的无网格拉格朗日粒子法。SPH方法思想简单,容易实现,一经出现便得到了迅速发展。相比较其他的无网格方法,它最大的优点是便于在大变形实际工程中应用,这一点是其他无网格方法无法比拟的[1]。在使用SPH进行模拟计算时经常会遇到界面处参数不连续的问题,通常SPH方法处理界面处的问题时,与连续体内部处理方法相同,会严重影响算法的准确性。M.B.Liu等[2]提出了1D不连续的SPH方法(DSPH),用来模拟不连续物理量,函数测试和一维激波管的模拟均显示了该算法的良好性能。赵燕等[3]推导了2D和3D不连续公式,并且解决了多维情况下确定不连续位置困难的问题。本文的主要工作是分析界面处该方法提高计算精度的本质原因,探讨DSPH方法如何应用于实际的物理问题中。
1 DSPH介绍
文献[3]基于Taylor公式推导了2D和3D的不连续SPH公式,给出了多维情况下不连续函数的粒子近似式和不连续函数一阶导数的粒子近似式
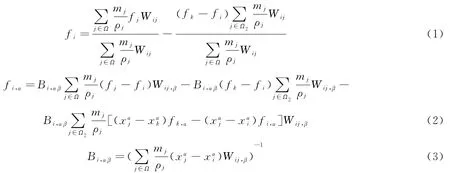
式中:W 表示核函数[1],mj、ρj分别为粒子j的质量及密度,α和β表示空间的维数。Ω为问题求解域,Ω1和Ω2为Ω的子域(Ω=Ω1+Ω2),函数或物理参数在Ω1和Ω2上分别连续,xi为Ω1上靠近不连续界面的一点,xk是Ω2上的任意一点,具体介绍见文献[3],其中
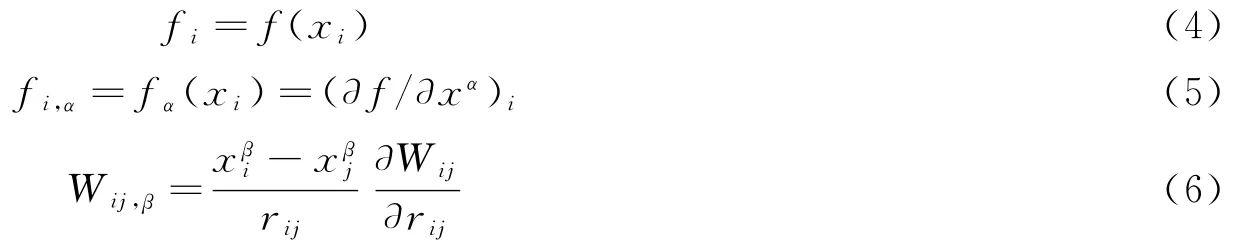
文献[3]中针对越过材料界面不连续物理量的计算,给出了大变形计算中确定不连续位置的方法,即根据颗粒材料属性是否相同确定是否为界面处。根据泰勒展开公式,从理论上给出了确定不连续公式中点xk的方法,并用数值方法验证了此方法的有效性。本文中将从理论上来探究该方法的有效性。
2 DSPH方法函数值计算的精确度探讨
文献[3]中已经证明了DSPH在模拟不连续问题时相较于SPH和CSPM所表现出来的优越性,同时也给出了3种不同粒子分布下DSPH所产生的误差大小。本文中将进一步针对粒子的均匀性对DSPH的影响进行研究。
粒子的分布情况如图1所示,粒子间距为1,粒子的自变量m的初始值为粒子下方的编号,核函数为三次样条函数,核函数的光滑半径取为h=1.5。函数形式为
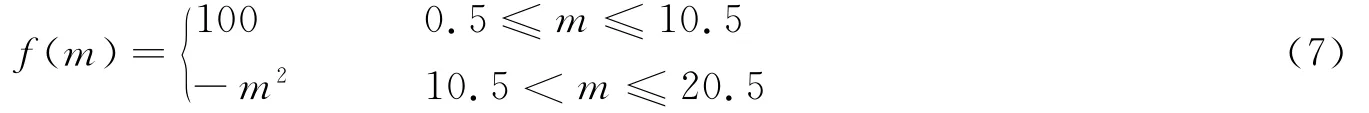
粒子11移动距离为x,-0.5≤x<0.5;粒子12移动距离为y,-0.5≤y<1。其他粒子均保持不动,改变x、y的值可以得到不同粒子分布情况下f(10)的函数值,不论粒子怎样移动,用DSPH方法所计算的f(10)的函数值的误差均为0。这说明了粒子11、12的值及分布情况对粒子10的计算结果不产生任何影响。

图1 粒子分布示意图Fig.1 The distribution of particles
下面探讨DSPH方法能够精确估算函数值的本质原因,由于式(1)中2部分的分母相同,因此只考虑分子的影响。将式(1)中2部分中的Ω写成Ω1和Ω2的和,结合文献[3]确定xk的方法可将式(1)写成如式下形式
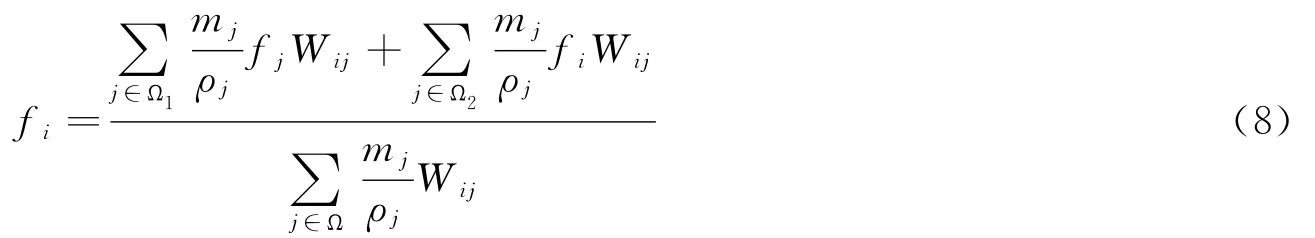
由式(8)可以看出,DSPH对函数值的估计的本质是:粒子i的函数值与它不连续界面异侧的粒子函数值无关,它的函数值取决于i同侧的粒子函数值,并且加大了粒子i本身在计算中所占的权重。Ω2中粒子的质量、密度及分布情况部分地决定了粒子i在估算点i处函数值时所占的权重。当使用DSPH方法处理边界问题时,Ω2中无粒子存在,DSPH方法与CSPM方法相同[1]。
在式(7)中,左侧粒子的函数若不是常函数,计算得到的f(10)的函数值则可能是不精确的,误差主要是由于SPH方法本身的特点引起的,因此在此没有必要讨论左侧粒子函数的变化对粒子10的影响。当搜索域足够小,搜索域内与被估粒子同侧的粒子函数可以认为是常函数时,可以保证被估粒子计算的精确性。
3 DSPH方法导数值计算的精确度探讨
与第2节类似,改变粒子的分布情况,检测DSPH在计算导数值时对粒子分布均匀性的敏感度,与图1相同,改变粒子11和12的位置,函数形式为
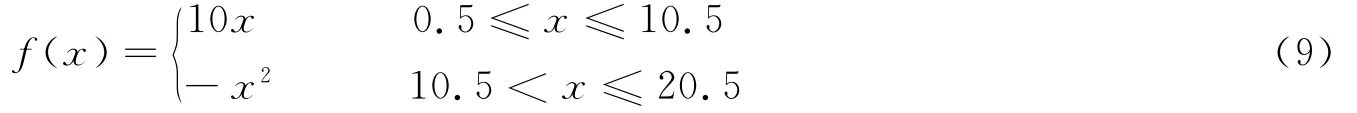
估算点10处的导数值,经过计算我们发现任意改变粒子11和粒子12的位置都不影响导数值计算的精确性。
下面通过DSPH方法的导数公式来分析产生这种现象的原因,与第2节类似,式(2)可改写为

在式(10)中,令Fi=xif′i+fi,Fj=xjf′i+fi,则式(10)可写为
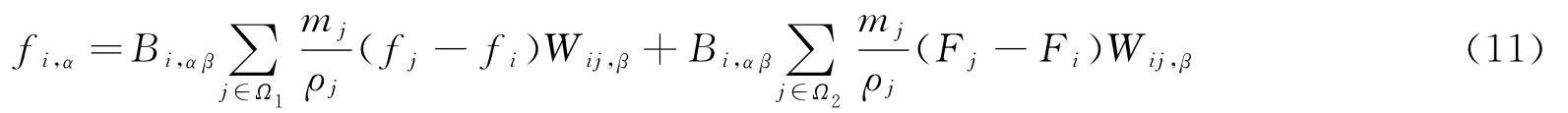
式(11)中的第2项Fi的含义是以点i处导数值为斜率,以fi为截距虚拟出一条直线来,在新的函数形式下估算粒子i的导数值,粒子i导数值的估算与异侧粒子的原函数形式没有关联。因此当与被估粒子同侧的函数为线性函数时,计算得到的被估粒子的导数值是精确的。由此不难推得,当不连续函数为多次函数时,只要粒子的搜索域足够小,搜索域内与被估粒子同侧的粒子函数可以认为是线性函数时,可以保证被估粒子导数值计算的精确性。
4 物理计算中不连续参数分析
SPH方法是一种拉格朗日方法,总的来说拉格朗日描述下的流体控制方程可写作一系列偏微分方程,即著名的Navier-Stokes方程,用SPH公式解Navier-Stokes方程组就可以得到SPH方法中的密度、应变率、加速度和能量的表达式。实施SPH方法的过程是通过应用局部区域内的相邻粒子对应的值来叠加求和取代场函数及其导数的积分表示形式[1]。从加速度计算的推导过程[4]可知,计算加速度需要考虑作用在该点的力,即使是在界面处,只要有相互作用,就需要考虑作用力,因此仅考虑在计算密度、应变率和能量时使用DSPH方法。由Navier-Stokes方程的表达式可知这3个物理量之所以存在不连续问题,本质上都是由于界面处速度的不连续引起的。根据式(2)可以得到速度梯度的DSPH表达式

式中:Bi,βγ的含义与式(3)类似。
将式(12)带入Navier-Stokes方程就可以得到相应的密度、应变率和能量的DSPH表达式。
4.1 密度
计算模型如图2所示,铝块的初速度为零,粒子间距为5mm,总粒子数为400。对右侧铝块的最右侧一排粒子施加水平方向上的约束。Mie-Grüneisen状态方程参数和Johnson-Cook材料屈服模型参数均来自文献[5-6]。各个参数有如图3所示的相互影响关系,在计算中加入了了人工黏性,系数为0.6、0.6、0.1。
钢块的初速度为140m/s,时间步长t=50ns。图4中给出了SPH方法和DSPH方法计算得到的1400步时物体的变形情况,SPH的计算结果中,钢块在撞击铝块后粘在了铝块上左右震动,如图4(a)所示,铝块的粒子出现断裂并且钢铝界面处粒子杂乱。在DSPH的计算结果中,钢块在撞击铝块后被反弹,两物块在界面处变形较小,如图4(b)所示。图5中给出了1 400步时左侧钢块的密度分布,粒子编号规律为:先对左侧物体编号,自底部粒子开始,最右侧一排粒子编号为1~10,右起第2排粒子编号为11~20,以此类推。可以看出距离界面越近,密度的计算值越不准确。这说明在界面处传统的SPH方法处理参数不连续时所存在的缺陷,同时也说明边界处理不好,会严重影响非边界处粒子物理量的计算精度,与之相对应的DSPH方法所计算出的密度值非常精确,改善了模拟结果。

图2 计算模型Fig.2 The model of simulation
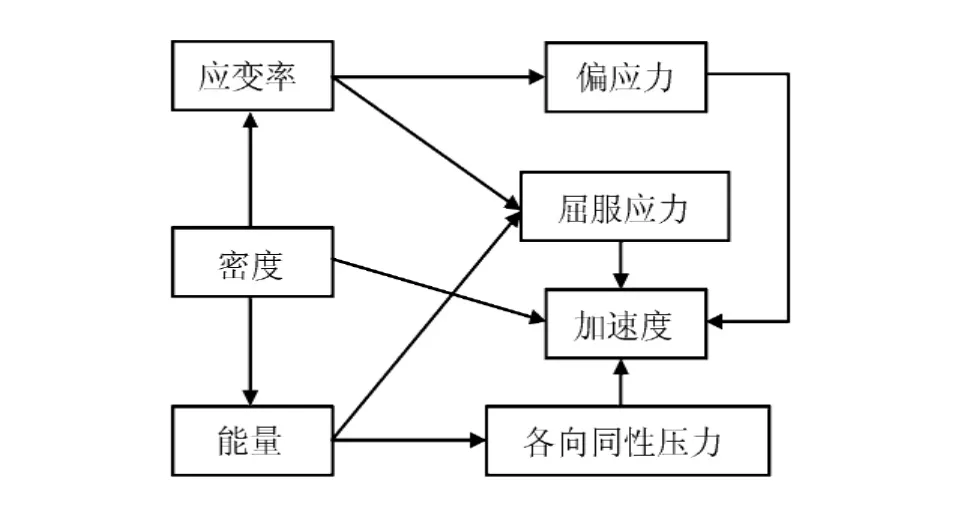
图3 各参数之间的相互关系Fig.3 The relationship between the parameters

图4 1400步时物体的变形情况Fig.4 The deformation of targets in 1 400th step
为了进一步说明DSPH方法计算结果的准确性,将左侧钢块的初速度提高到300m/s,时间步长t=5ns。图6是1 200步时SPH和DSPH的计算结果,图7是分别使用SPH方法和DSPH方法得到的点A(位置如图6所示)处的应力应变曲线,将2种计算结果与理论值相比较,可以看出DSPH很好地改善了界面处的模拟精度。
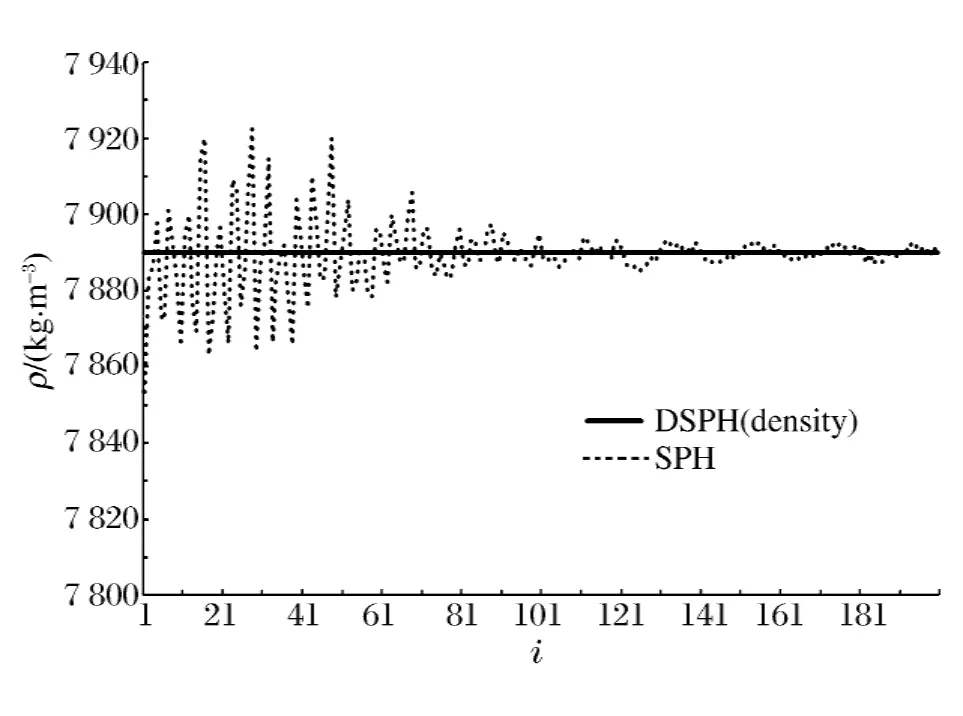
图5 1400步时钢块上的密度分布Fig.5 The density in different particles of steel in 1 400th step
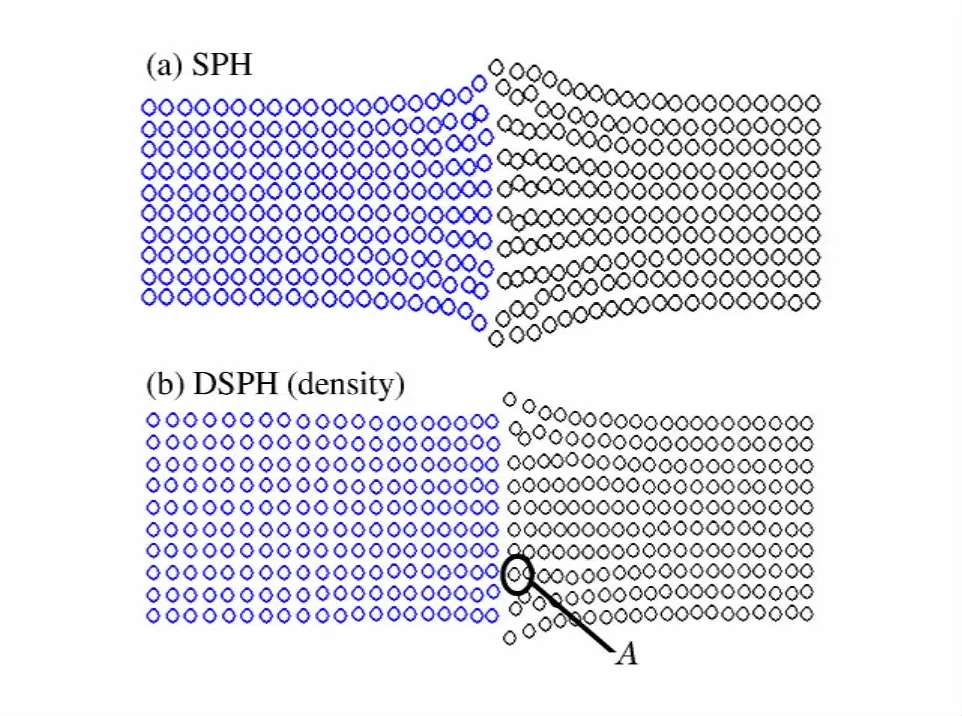
图6 1200步时物体的变形情况Fig.6 The deformation of targets in 1 200th step
连续介质力学中连续性方程的推导过程,可反映出对于固体,若界面处存在速度的不连续,则需要在计算密度时使用DSPH方法[4],这一结论同样适用于同种材料的界面问题。将图6中的算例改为2个钢块对碰,输出各个粒子的密度值以及点A处的应力应变曲线,可以发现,在此类问题中,DSPH方法的计算结果同样优于SPH方法。当界面两侧不存在相对速度时,无论是同种材料还是不同材料物体的界面问题,SPH方法都能较为精确地计算密度值,就没有必要使用DSPH方法了,对此我们也做了相应的模拟,2种方法计算得到的结果相同。
当然以上理论仅针对固体而言,对于等体积内质量会发生变化的问题而言,比如不同气体的渗入、液体混合等就不推荐使用DSPH方法来计算密度。
SPH中计算密度的另一种方法是密度求和法[1],密度求和法体现了SPH近似法的本质,但在实际的程序计算中,该方法计算效果很差。有许多改进该算法的修正方案,比如目前较常用的CSPM方法,但是CSPM方法在求解含间断算例时却存在计算不稳定的问题[7],若使用该方法计算密度,则需限定接触的两个物体为同种材料。使用DSPH方法可以摆脱这一限制,根据式(1)可得到密度求和法的DSPH表达式
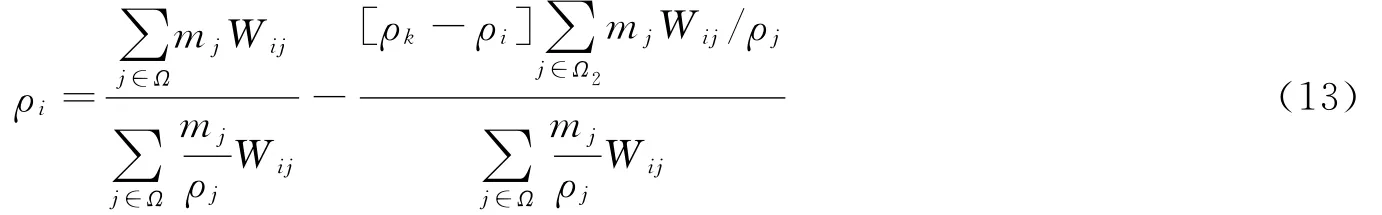
式(13)右边的第1项与CSPM方法相同,第2项是通过对密度非连续性进行处理得到的。使用与图4相同的计算模型,从图8中可以看到,CSPM方法的模拟结果很不理想,钢块在界面处收缩,而铝块在界面处扩张,最终由于变形过大而导致计算不能继续进行。而DSPH方法的计算结果与图4(b)相同,密度计算值精确度与连续性密度法(DSPH)基本相同。这证明了DSPH方法在处理界面不连续问题时优于CSPM方法。

图7 点A处的应力应变曲线Fig.7 The stress-strain curve in particleA
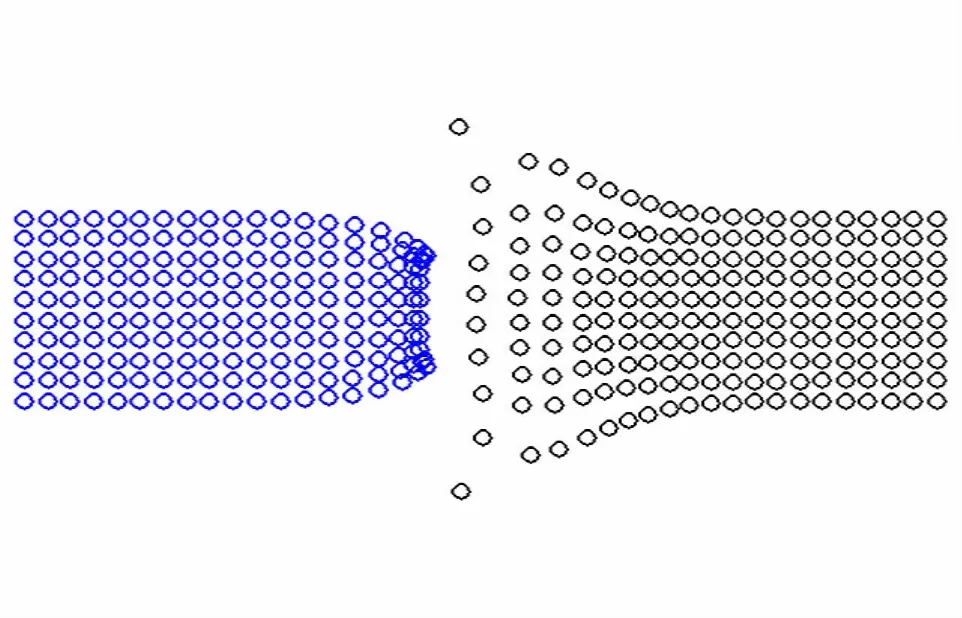
图8 两物体变形情况Fig.8 The deformation of targets
4.2 应变率
由图3可知,应变率的计算主要是影响了偏应力和屈服应力的计算,为了说明应变率在使用DSPH方法后对结果的影响,左侧的钢块以初速20m/s的速度正碰右侧的钢块(加速度是由各向同性压力和偏应力共同影响的[1],速度过大时物体会产生变形,偏应力相较于各向同性压力较小,不利于说明应变率改变对结果的影响),计算模型如图2所示,时间步长t=50ns,未使用人工黏性。由同种材料物体的碰撞规律可知,在撞击后左侧钢块静止。图9是计算得到的左侧钢块速度随时间的变化曲线,可以看出应变率的DSPH方法对模拟结果的改善。
并不是在所有界面处都可以使用DSPH方法计算应变率,当界面处速度连续,比如两种材料组成的组合梁,在梁纵向对称面内作用一对力偶矩,使梁产生弯曲变形,此时界面处应力不连续,但应变是连续的[8],使用DSPH方法计算应变率后会导致界面处变形不一致,两材料在界面处脱离,传统的SPH方法保证了变形的连续性。
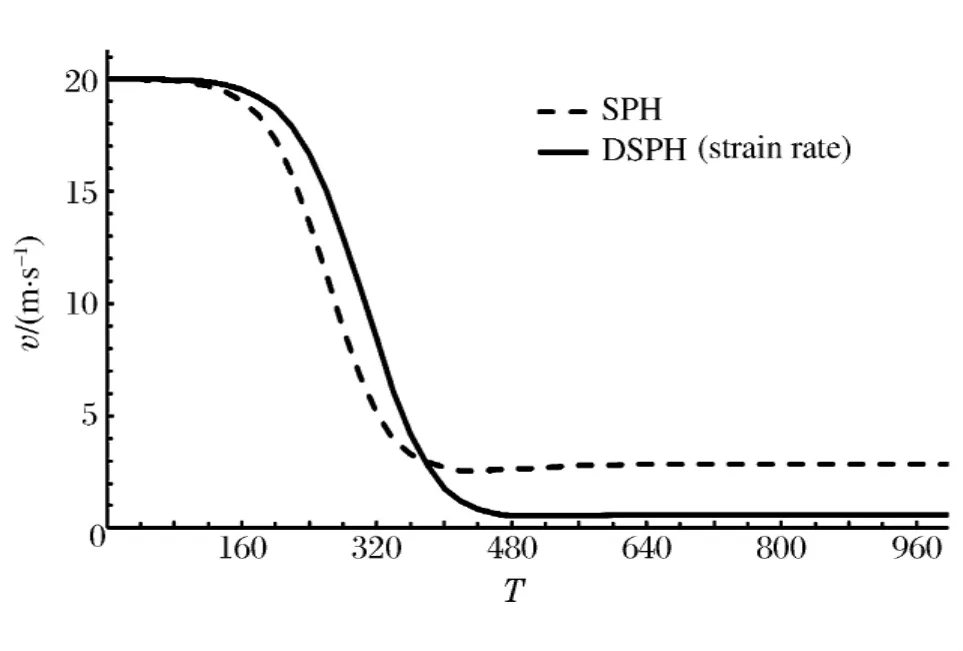
图9 左侧钢块速度随时间步的变化情况Fig.9 The velocity of steel in different time steps
4.3 能量
由图3可知,能量的计算只影响后续两个物理量的计算:各向同性压力p及屈服强度Y。对于固体来说密度值为常数,使用 Mie-Grüneisen状态方程计算各向同性压力p,由p的表达式[1]可知若密度计算不准确,将影响p与能量之间的线性关系。所以考虑在对密度使用DSPH方法的基础上,讨论对能量使用DSPH方法对结果的影响。计算模型与图6相同,速度为300m/s,输出图6中点A处的能量变化可得图10,两曲线分别为对密度使用DSPH方法(d)和对密度、能量同时使用DSPH方法(ed)得到的,两者有一定的差异。图11中是两种方案得到的各向同性压力p和屈服强度Y的曲线图,可以看到与p的表达式所显示的一样,各向同性压力p与能量的变化趋势相同,屈服强度Y的差别较小。提高撞击速度,两种算法计算出的能量差异会更大,相应的各向同性压力和屈服强度的差异也较大,但是对加速度并没有影响,同一时刻两种方法得到的变形图基本相同,因此我们认为在固体冲击问题的计算中没有必要对能量使用DSPH方法进行计算。
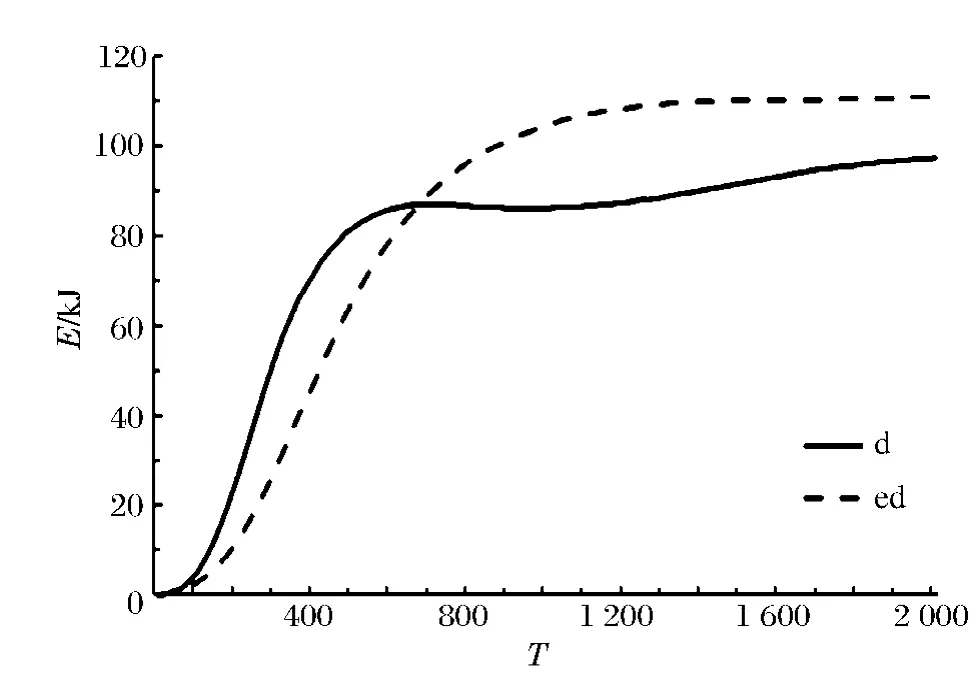
图10 能量随时间步的变化Fig.10 The energy in different time steps
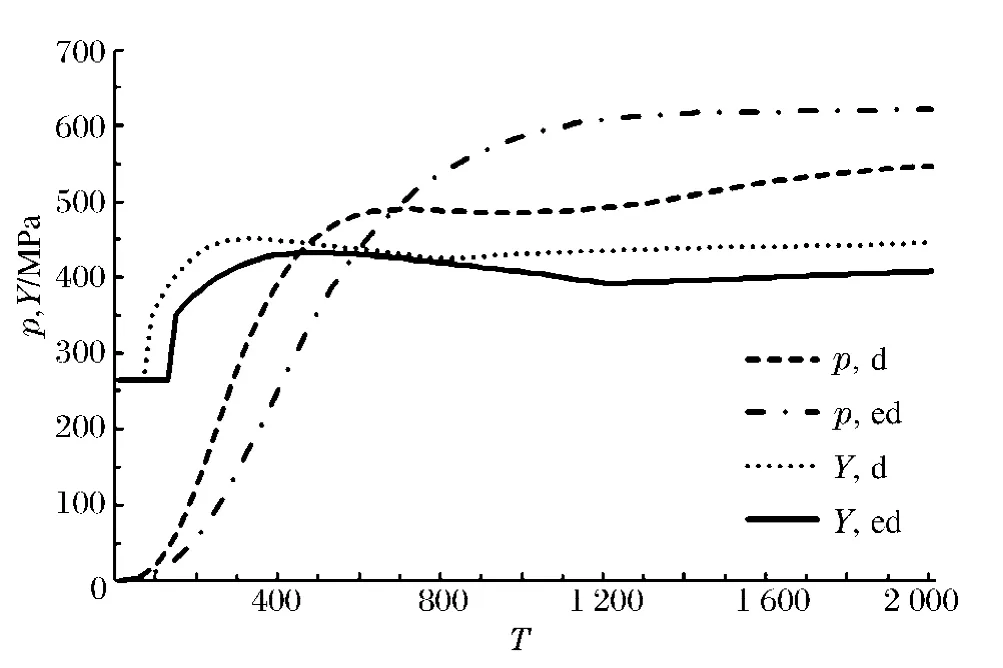
图11 各向同性压力p和屈服强度Y随时间步的变化Fig.11 The isotropic pressure pand yield strength Y in different time steps
5 结 论
通过对DSPH计算公式的推导分析,发现DSPH方法之所以能够很好地处理界面问题,本质原因在于DSPH方法计算函数值及导数值时忽略了在不连续界面异侧的粒子对被估粒子的影响,按照同等比例加大了被估粒子本身对结果的影响。
通过对碰模型考察了DSPH方法在计算密度、应变率及能量这3个物理量时所产生的影响,三者的实质都是考虑了界面处的速度不连续。密度计算的准确性在整个计算中起着至关重要的作用;在偏应力相较于各向同性压力不可忽略的问题中使用DSPH方法计算应变率会对结果产生一定的影响;DSPH方法对能量计算的影响并不大。在计算中密度和应变率在使用DSPH方法时是相互独立的,可同时使用,共同提高计算精度。
在本文的模拟中只是使用了简单的对碰模型,今后需要将此方法应用于更为复杂的物理问题中,以进一步验证该方法的有效性,更好地发挥DSPH解决边界问题的优势。
[1]韩旭,杨刚,强洪夫.光滑粒子流体动力学—— 一种无网格粒子法[M].长沙:湖南大学出版社,2005:35-323.
[2]Liu M B,Liu G R,Lam K Y.A one-dimensional meshfree particle formulation for simulating shock waves[J].Shock Waves,2003,13(3):201-211.
[3]赵燕,徐绯,李玉龙.一种可考虑界面不连续的改进SPH 方法[J].计算力学学报,2009,26(6):928-934.Zhao Yan,Xu Fei,Li Yu-long.An improved SPH method in the discontinuous interface problem[J].Chinese Journal of Computational Mechanics,2009,26(6):928-934.
[4]黄筑平.连续介质力学基础[M].北京:高等教育出版社,2003:125-143.
[5]Morris J P.Analysis of smoothed particle hydrodynamics with application[D].Australia:Monash University,1996.
[6]Katayama M,Toda S,Kibe S.Numerical simulation of space debris impacts on the Whipple shield[J].Acta Astronautica,1997,40(12):859-869.
[7]Zukas J A.High velocity impact[D].New York:John Wiley and Sons,1990.
[8]苟文选.材料力学[M].北京:科学出版社,2005:215.
