空间站对接碰撞能量计算的简化分析
2013-09-19肖余之时军委胡雪平
肖余之,时军委,胡雪平
(1国防科技大学航天科学与工程学院,长沙410073;2上海市空间飞行器机构重点实验室,上海201108)
1 引言
随着我国载人航天技术的持续发展,建立空间站已成为下一步的任务目标。国外的空间站建立较早,主要有俄罗斯/前苏联的“礼炮”号系列空间站、“和平”号(MIR)空间站,美国的“天空实验室”,欧洲航天局的空间实验室(Spacelab),以及由美、俄、日、欧洲等16国及地区组织共同建设的国际空间站(ISS),这些空间站的建造和运营过程中都使用了交会对接技术[1]。对接机构可以分为锥杆式和周边式,锥杆式碰撞能量的计算相对简单,由于周边式几何构型复杂,其碰撞能量的计算十分复杂,传统方法都是通过数值积分解决。
未来我国空间站从“I”字构型变为“L”字构型再变成“T”字构型的建造过程中,以及载人飞船和货运飞船来访的运营过程中都需要通过-V-Bar对接完成。对接过程是典型的动力学[2]过程,两航天器以一定的相对速度接近,直到主、被动对接机构的对接环相互碰撞、捕获,然后缓冲相对运动的能量。对接机构的缓冲系统必须在确保捕获的前提下在有限位移和转角内缓冲并消耗掉碰撞产生的能量,使得两航天器相对运动停止并对准,为拉近和刚性连接做好准备。
对接碰撞的能量除与对接初始条件相关外,还与对接航天器的质量、惯量以及航天器是否存在偏心有关。在天宫一号与神舟八号对接时两个航天器吨位比较接近,而空间站对接时目标航天器的吨位、惯量以及构型都有比较大的变化。比如空间站为“I”字构型时对接,碰撞能量主要集中在对接机构的轴向,其它方向相对较小;空间站为“L”构型时,由于偏心的原因将使得轴向碰撞引起空间站的旋转,轴向能量向偏转方向有能量转化,使得偏转方向上的能量增加很多;空间站为“T”字构型时,由于其惯量增加很多也会导致碰撞能量上升。根据空间站的建造和运营过程中的对接需求,对各种对接碰撞产生的能量进行计算,并根据对接机构的适应能力进行方案的选择。
本文就任意两航天器的碰撞式空间对接,建立了三维等效模型来计算碰撞产生的能量,并根据空间站构型将三维模型合理简化成二维模型,并对空间站“I”字、“L”字以及“T”字构型时的对接碰撞能量进行了分析。二维模型能够直观、方便、快速的计算空间站对接过程中碰撞产生的能量。
2 三维模型
航天器的对接撞击发生在很小的区域,因此可以把两个航天器看成除相互碰撞点外都是刚性体的撞击过程[3]。如图1,分析两个质量、转动惯量和质心分别为mi和Ii和oi(i=1,2)刚体的撞击过程。坐标系oxyz为地心惯性坐标系,o1x1y1z1和o2x2y2z2分别为两航天器的本体坐标系,坐标轴为航天器的惯性主轴。
两航天器的平动和转动方程为,
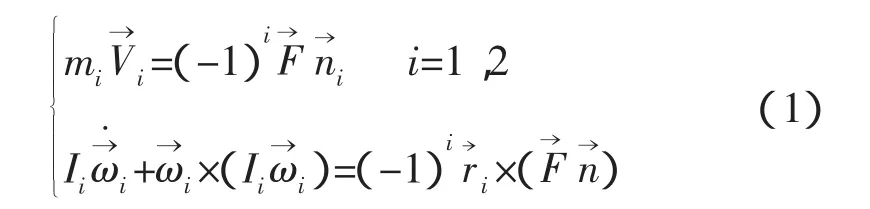
两个刚体的运动方程由碰撞点的联系方程关联。联系方程为:相互接触点的速度之和与对接机构在接触点沿公法线方向的投影和相等[2],即
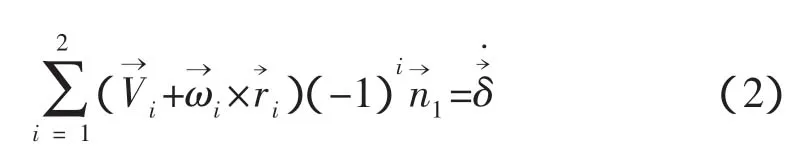
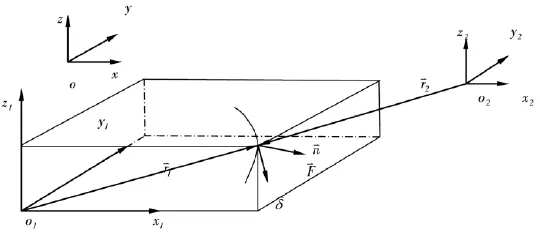
图1 两航天器相互碰撞示意图
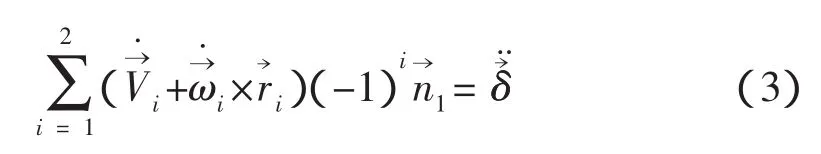
将动力学式(1)代入上式得,

上式即为等效的动力学方程,这样就把两对接航天器的相对运动和碰撞问题简化为一个具有等效质量、惯量的物体与一个仅有几何形状的固定障碍物的撞击。对应的等效质量为mδ,
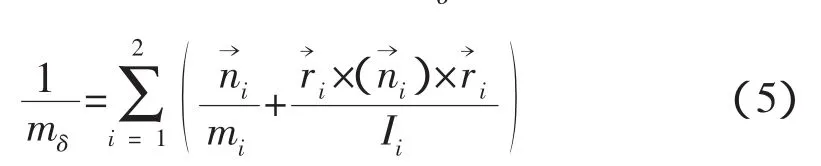

异体同构对接机构有22种接触情况[4],即使在简化的情况下分析也是复杂的,通常需要通过求解式(4)的常微分方程才能给出准确的碰撞能量。空间站对接时,航天器的吨位比较大,式(5)的等效质量主要取决于航天器的质量、惯量和质心位置矢量,可以根据空间站航天器的特点做进一步的简化。
3 平面模型
3.1 等效模型的建立
如图2所示,坐标系oxyz为惯性坐标系,o1x1y1z1和o2x2y2z2分别为两航天器的本体坐标系,坐标轴为物体的惯性主轴,o3x3y3z3表示主动对接机构安装坐标系,其中o3位于主动对接机构在航天器的安装点。航天器i在平面内转过的角度为θi;矢量与水平方向的夹角为αi,与航天器i轴线的夹角为βi。根据几何关系有,
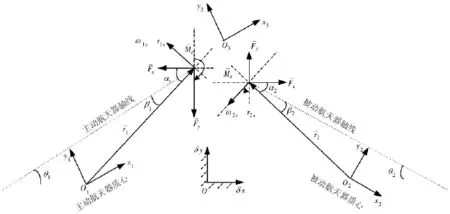
图2 平面模型图

两航天器的平动和转动方程(1)式在图2的平面情况下为,
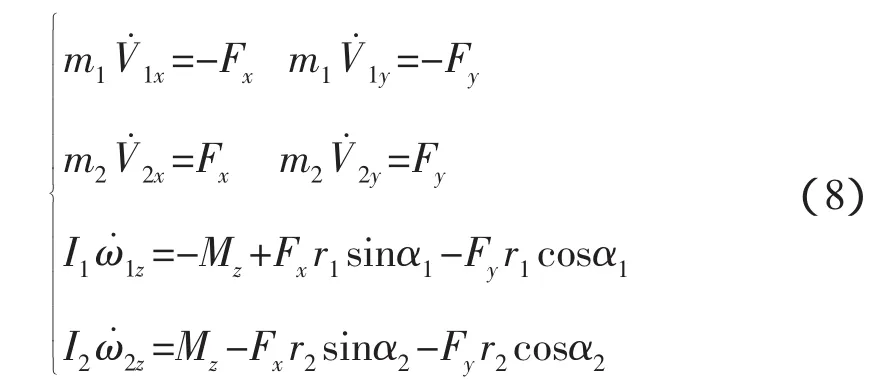
这时接触点的联系方程式(2)为,
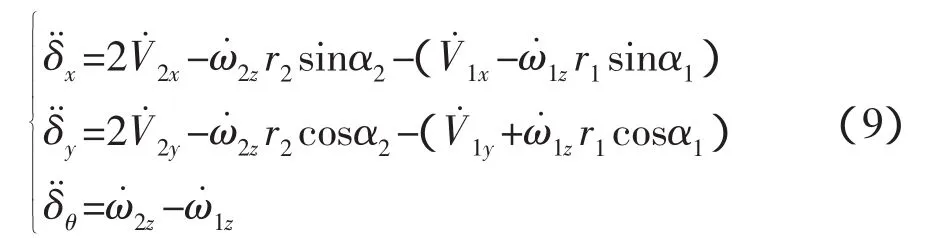
考虑初始条件范围内(θ1,2≤5°),cosθ1≈1 联系方程式(9)投影到o3x3y3z3坐标系为

将动力学方程式(8)代入上式并整理得,
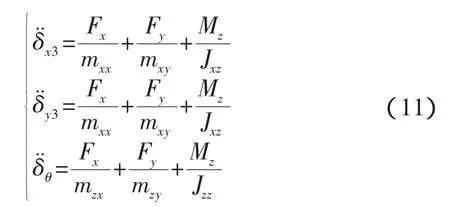
由于对接环的质量远远小于航天器的质量,其惯性对碰撞力的贡献可以忽略[2],并利用初始条件范围内cosθ1≈1,则缓冲系统力可以写成碰撞与速度的函数,具体如下,
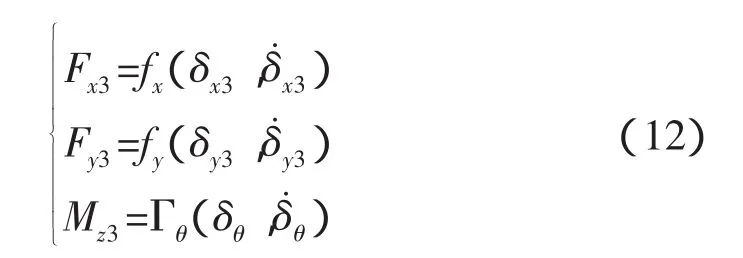
将上式代入式(11),即可得到对接环在O3系的动力学方程,
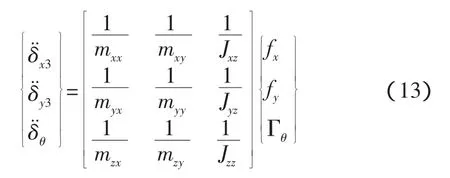
上式中各系数项即为等效质量、等效惯量,具体如下:


系数间有如下等式成立,证明(13)式中的等效质量阵为对称矩阵。
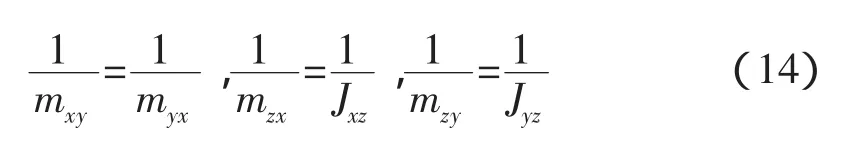
式(13)是一个基本的等效模型,在这个模型的基础上可以得到纵向、横向以及偏转方向缓冲模型的一些特点。
比如纵向等效质量mxx,航天器质心在其轴线上(βi=0)时的正碰(θi=0)情况下这与文献[5]的结果一致,具体为

如图3所示,主动航天器为“I”字构型飞船(α1=0),空间站为“L”字构型的正碰对接时,纵向等效质量为
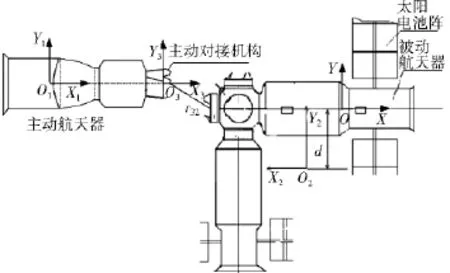
图3 空间站L构型对接示意图
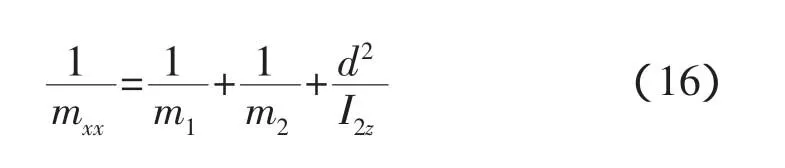
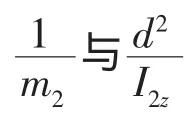
偏转方向的方程可以通过(13)式消去fx和fy得到,
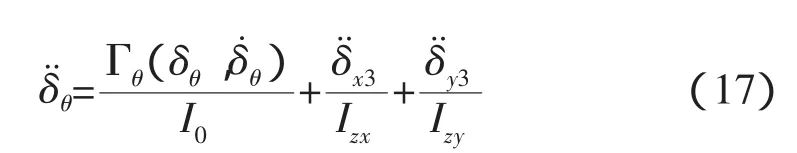
偏转方向的等效惯量I0如下式。
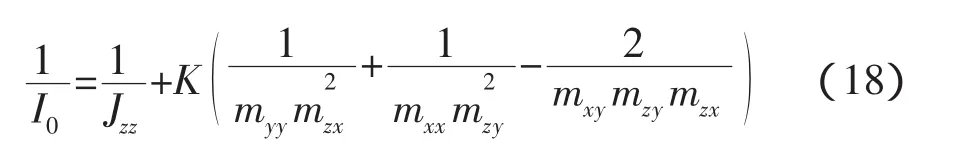
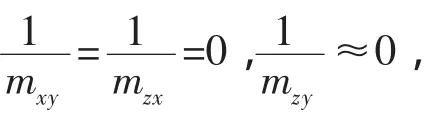
“L”构型的对接,式(18)中的各项都不为零,偏转方向的等效惯量与两个航天器的质量、惯量以及质心位置都有耦合,这恰好体现了偏心对接的复杂性。
3.2 初始条件的模型
按照式(6)求解碰撞能量还需要知道速度和角速度的初始值。对于周边式对接机构来说,捕获后的缓冲过程中纵向和滚转方向的运动衰减时间约几秒;横向运动的衰减时间约十几秒;而偏转方向的衰减时间长达几十秒乃至几分钟的量级。捕获后航天器相对角速度对大吨位或偏心对接来说是很重要的,假设纵向和横向分别受到冲量Nx和Ny作用并忽略力矩引起的冲量,根据动量守恒初始速度和变为零的条件为,
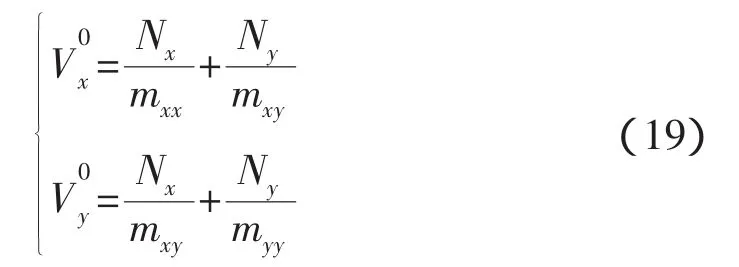
上式经整理可以求出冲量Nx和Ny,
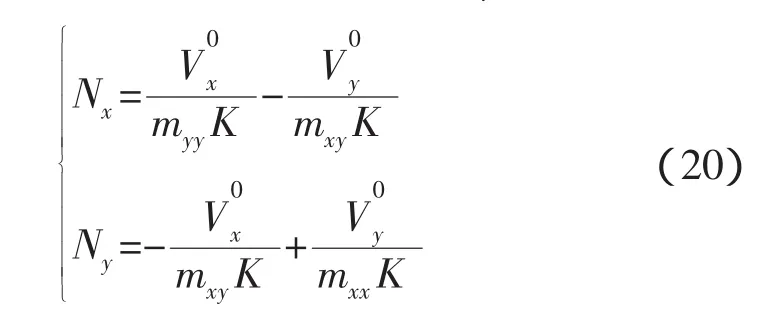
根据冲量Nx和Ny的作用,就可以计算捕获后的相对角速度,

上式经整理后得,
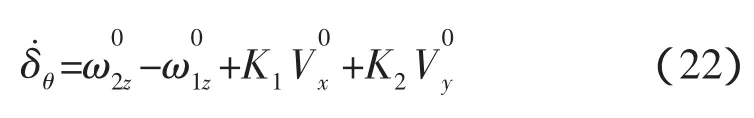
式中系数分别如下,
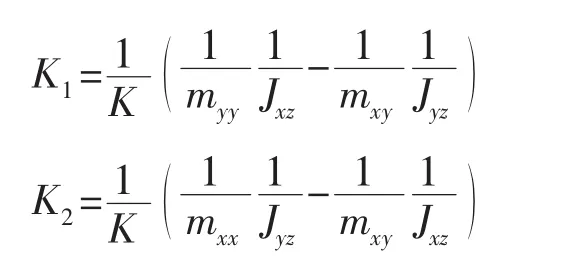
这样结合式(18)就可以对偏转能量进行分析。

从上式可以看出,同轴对接,纵向冲击不引起偏转角速度,但侧向撞击引起的角速度在目标航天器的质心距离对接面比较远时是不可忽视的,也就是说如果目标航天器是细长的‘I’字构型,要特别注意控制横向速度。
再来讨论图3中“L”构型的同轴偏心对接,有β1=0,且θ1=0;目标初始转角为零θ2=0,α2=β2。将这些条件代入式(13)的系数中重新求式(22),不考虑航天器的初始角速度,仅研究轴向和横向撞击引起的旋转为,
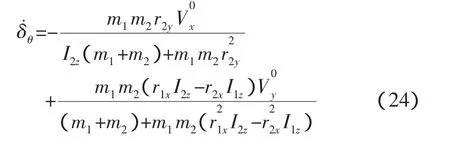
通过式(24)可以分别对轴向撞击或横向撞击引起的偏转速度进行分析。式(24)分为两项,前一项为轴向撞击引起的偏转,与偏心量r2y很相关,与主动航天器的惯量无关;后一项为横向撞击引起的偏转,与偏心量r2y无关。结合图3和式(24),轴向撞击引起的偏转角速度总是为负,只有在为负号时两者才可以叠加求得最大值,这与对接试验中的现象是一致的。
4 计算分析
有了纵向和横向的初始速度和角速度、等效质量和惯量就可以进行捕获后的分析。航天器“L”构型的质量和机构的特性分别按文献6、7进行算例分析,计算结果如下。
(1)轴向撞击引起的角速度为1.0°/s;横向撞击引起的角速度为 1.4°/s,两者之和为 2.4°/s,该值是航天器相对偏航初始角速度的3倍。可见在偏心情况下,无论是轴向撞击引起的偏转角速度,还是横向撞击引起的偏转角速度都是不可忽略的。
(2)如图4所示,为机构偏转缓冲能量与空间站对接碰撞能量消耗需求关系。空间站各种构型对接碰撞产生的能量在20J~200J之间,远超过机构40J的承受极限,当空间站的构型与质量特性已定时,降低轴向速度和横向速度是降低碰撞能量有效措施。
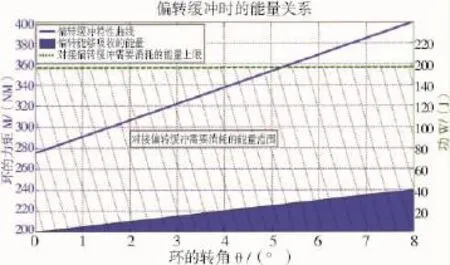
图4 偏转缓冲时的能量关系
5 结论
本文就任意两航天器碰撞式对接,建立三维等效模型计算碰撞能量,根据空间站构型将三维模型合理简化成二维模型,二维模型无需求解常微分方程,并对空间站“I”字、“L”字构型以及“T”字构型时的对接碰撞能量进行了分析。简化模型能够直观、方便、快速地计算对接碰撞产生的能量。◇
[1]林来兴.自主空间交会对接技术进展.载人航天,2005,(4):13-17.
[2]娄汉文,曲广吉,刘济生.空间对接机构.航天工业出版社1992.
[3] W.J.Stronge,Impact Mechanics,Cambridge University Press 2000.
[4]王兴贵等,周边式对接机构的航天器首次接触撞击点的确定宇航学报,1999,1(1):50-57.
[5]洪嘉振.计算多体系统动力学.高等教育出版社,1999.
[6]张崇峰,肖余之等.航天器对接机构缓冲器的设计研究,哈尔滨工业大学学报,1998,30(5):112-115.
[7]李广兴,肖余之等.空间站组装过程姿态控制方案研究,载人航天.2012,18(1):22:29.
[8]赵阳,曹喜滨等.空间对接机构缓冲元件吸能分配,振动工程学报,2000,13(3):439:442.
