对接初始条件对捕获概率的影响分析

郑云青，张崇峰，刘 志，顾 靖

（1上海市空间飞行器机构重点实验室，上海宇航系统工程研究所，上海201108；2上海航天技术研究院，上海201109）

1 引言

两个航天器在空间进行交会对接时，可分为两个阶段：交会阶段和对接阶段。在两航天器第一次机械接触之前称为交会阶段，主要完成追踪航天器与目标航天器的交会、接近，将两航天器的相对位置、姿态和相对速度调整到对接初始条件范围内。从两航天器第一次机械接触开始，关闭姿态控制系统，由对接机构机械系统完成碰撞连接、轴向捕获、相互拉紧，直到两航天器完成刚性连接连成一个整体，称为对接阶段[1]。

两航天器对接时，由于敏感器测量误差、控制系统精度所引起的动力学误差以及测量装置和对接机构的安装误差等相互叠加，其相对运动参数总是有偏差的[2]，即两航天器捕获时，总是在一定的初始条件范围内进行的。由于这种偏差的客观存在，使航天器的交会与对接变得复杂了，也给对接机构的成功捕获增加了难度。

对接机构有多种类型，如“锥－杆”式、“锥－栓”式、异体同构周边式、数控式以及“十字型”布局小型卡爪式对接机构等[3，4]。这些对接机构的结构形式不同，但主要工作过程是一致的。本文以异体同构周边式对接机构为例，根据GNC能够实现的对接初始条件规律和范围，提出了对接机构捕获概率计算的方法，分析了对接初始条件的分布范围和规律对捕获概率的影响。

2 对接过程简介

异体同构周边式对接机构是按照雌雄同体的配合原则配置对接面的部件，所有对接面的部件都相对于同一轴成对地反对称放置，即凸部对凹部、销对套、主动对被动等，以保证两对接机构之间的相容性，见图1。根据这一原则设计的对接机构，主被动为一体，无须区分主被动部件，这样可以保证一艘飞船可以与装有相同对接机构的任意飞船对接。

图1 异体同构周边式对接机构

异体同构周边式对接机构由与捕获缓冲有关的对接环、捕获锁、传动缓冲机构以及与密封有关的连接密封机构等组成。对接机构的捕获缓冲过程[5]见图2。具体为：

①对接准备：对接前，将追踪航天器对接机构的对接环推出到准备对接位置，并使对接环在位置和姿态上具有一定的柔性；

②接触、缓冲：在对接初始条件范围内，当两对接机构第一次机械接触时，追踪航天器和目标航天器的对接环相互配合，利用自身的结构形状进行初始导向，并通过传动缓冲机构缓冲两航天器间的碰撞；

③捕获：当两对接环端面重合时，追踪航天器的捕获锁与目标航天器的挡块咬合，实现捕获；

④缓冲与校正：追踪航天器的对接机构通过传动缓冲机构对两航天器间的相对运动进行缓冲，校正两航天器间的姿态和位置偏差。

3 捕获概率定义

3.1 对接初始条件及其分布函数

对接初始条件是在目标航天器对接面坐标系下描述。目标航天器对接面坐标系Od-XdYdZd如图3所示，坐标系原点Od在目标航天器对接框端面中心，OdXd轴指向目标航天器后端。追踪航天器对接面坐标系Oz-XzYzZz的坐标系原点Oz在追踪航天器对接环环导向板根圆圆心，OzXz轴指向追踪航天器前端。

对接初始条件是指两航天器对接机构首次机械接触时，追踪航天器对接面坐标系与目标航天器对接面坐标系之间相对同轴位置偏差的相对坐标值（相对位移与相对转角）及其一阶导数（相对速度与相对角速度），即包括：

① 接近速度Vx；

② 横向偏移量 ΔY、ΔZ；

③ 横向速度Vy、Vz；

④ 横向角偏移量Ψ、θ；

⑤滚转角偏移量φ；

⑥ 横向角速度 ωΨ、ωθ；

⑦ 滚转角速度ωφ。

对接初始条件由航天器的姿态控制系统实现，其分布密度函数为：

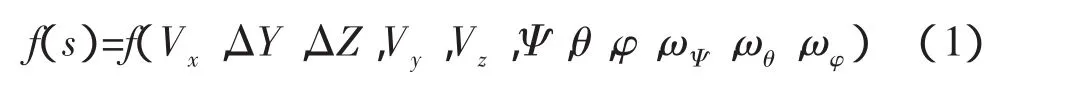
初始条件的各自由度是相互独立的。在任一对接工况下，对接初始条件是由上述初始条件参数随机抽样组合形成的。根据相互独立的多维随机变量的特性[6]，存在：

图2 对接机构的捕获缓冲过程

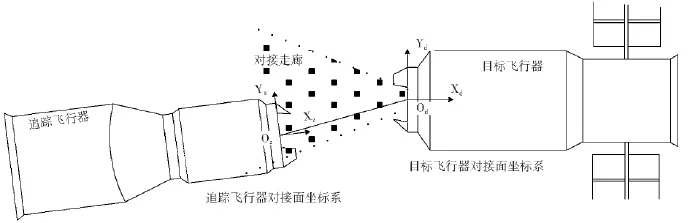
图3 对接坐标系

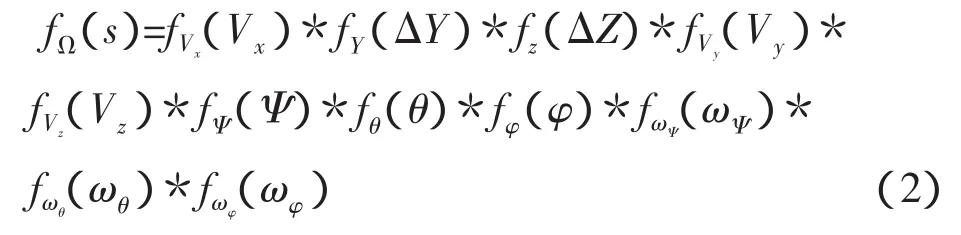
令

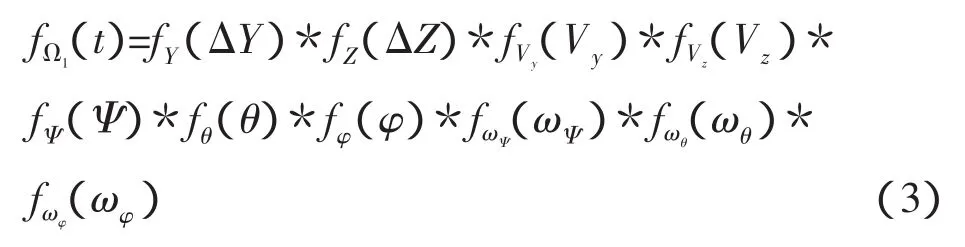
f（s）的定义域为航天器姿态控制系统实现的对接初始条件范围，记为Ω。Ω1为除Vx外其它自由度形成的初始条件范围，称为对接初始条件偏差。在定义域Ω内，随机变量s的累积概率值为：

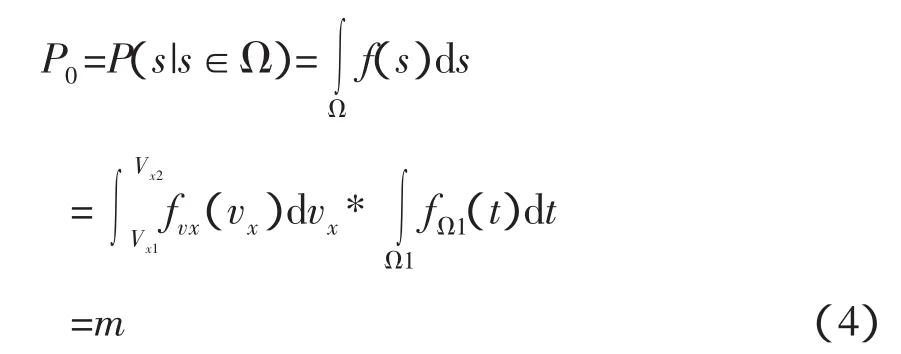
3.2 捕获概率

捕获概率是指在对接初始条件范围内，追踪航天器对接机构与目标航天器对接机构能够捕获成功的概率。

由于初始条件的不同，虽然对接机构的工作是正常的，两航天器仍然可能捕获失败；若改变对接的初始条件，则两航天器就能捕获成功。因此，捕获概率仅与对接初始条件范围和对接机构捕获缓冲能力有关，而与对接机构的可靠性无关。

在对接机构正常工作情况下，某次具体对接初始条件工况下的捕获试验，只存在两种结果，即捕获成功或捕获失败。因此，在一定的对接初始条件范围Ω2内，对接机构能够捕获；超出此范围，则不能捕获。

在两航天器接近对接时，为了保证捕获缓冲的顺利进行，两对接航天器的对接环可以按照六个自由度逐渐靠近，直到重合在一起，实现两环同轴，并在重合时完成捕获。

在对接捕获过程中，必须具有足够的能量将捕获锁的锁舌压入到导向板锥面下，之后，捕获锁锁舌迅速弹出，与目标航天器的挡块啮合，从而实现两航天器的捕获，如图4所示。因此，两航天器应具有一定的沿X轴的纵向接近速度，且必须保证纵向速度的下限，即：

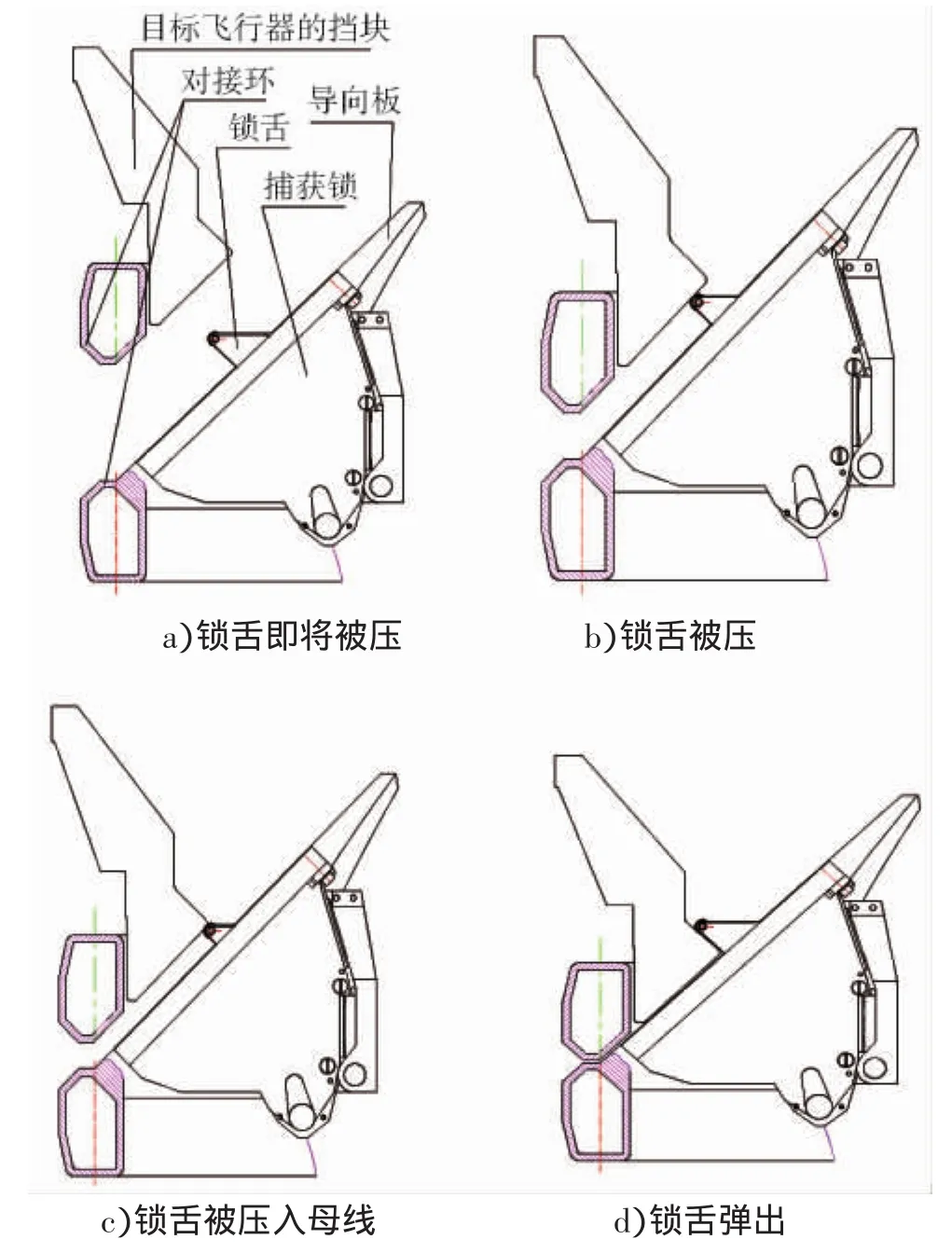
图4 捕获锁锁舌压入过程示意图

实际上，在捕获之前，部分能量要消耗在由对接初始条件偏差引起的撞击上，导致捕获时航天器的接近速度Vx与开始相比减小了。任意对接初始条件偏差下的最小捕获速度Vxmin是由产生捕获锁锁舌压入力的纵向速度和对接初始条件偏差决定的，且Vxmin随着对接初始条件偏差的增大而增大，即：

在对接初始条件范围Ω内，对接机构能够捕获的范围为：

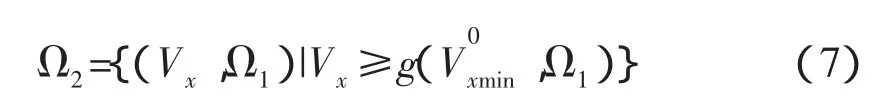
对接机构能够捕获的累积概率值为：

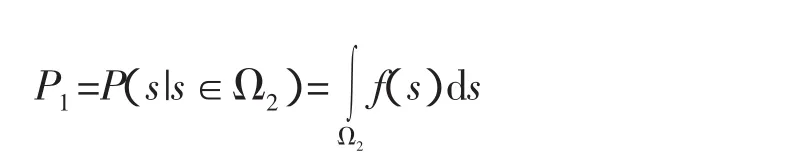
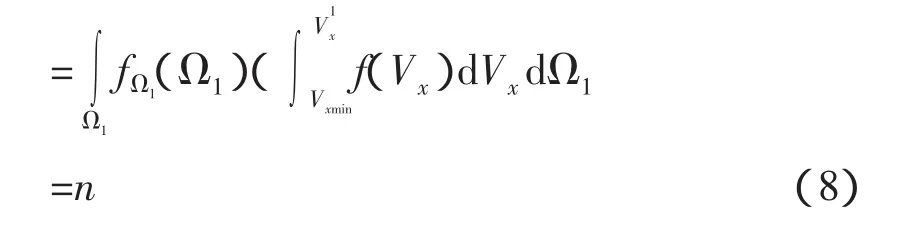
根据捕获概率的定义，在对接初始条件分布范围Ω内，对接机构的捕获概率为：

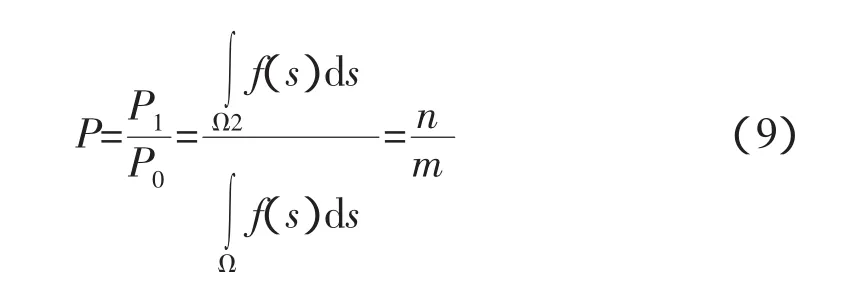
4 对接初始条件分布规律对捕获概率的影响

根据仿真分析，在对接过程中，两航天器的横向偏差对最小纵向接近速度影响较大。为了了解初始条件对捕获概率的影响，以两航天器对接过程中只存在横向Y、Z向偏差，其它的对接初始条件偏差均无偏差为例进行计算，其中Vx的范围是［Vx1，Vx2］，横向的对接最大偏差为±R，其中：

假设对接机构能够捕获的最小纵向接近速度Vxmin随着R2的增大线性增加，即

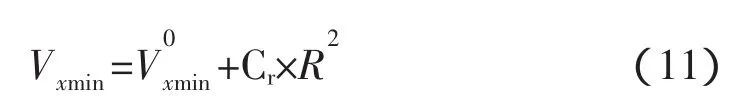
式中Cr：为Vxmin的线性增大系数。

4.1 对接初始条件分布规律与捕获概率的关系

对接初始条件的分布分以下几种情况：

①Y、Z的偏差和Vx的分布都服从正态分布，都在3σ范围内，此时：

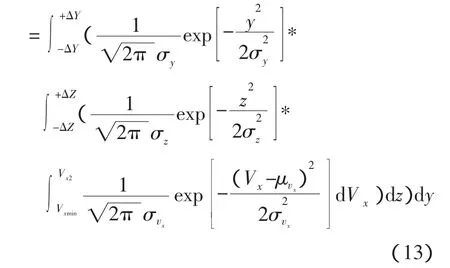
式中：σy=ΔY/3

σz=ΔZ/3

σvx=（Vx2-Vx1）/6

μvx=（Vx2-Vx1）/2

②Y、Z的偏差服从正态分布，在3σ范围内；Vx的分布服从对数正态分布，log（Vx）在3σ范围内，此时：

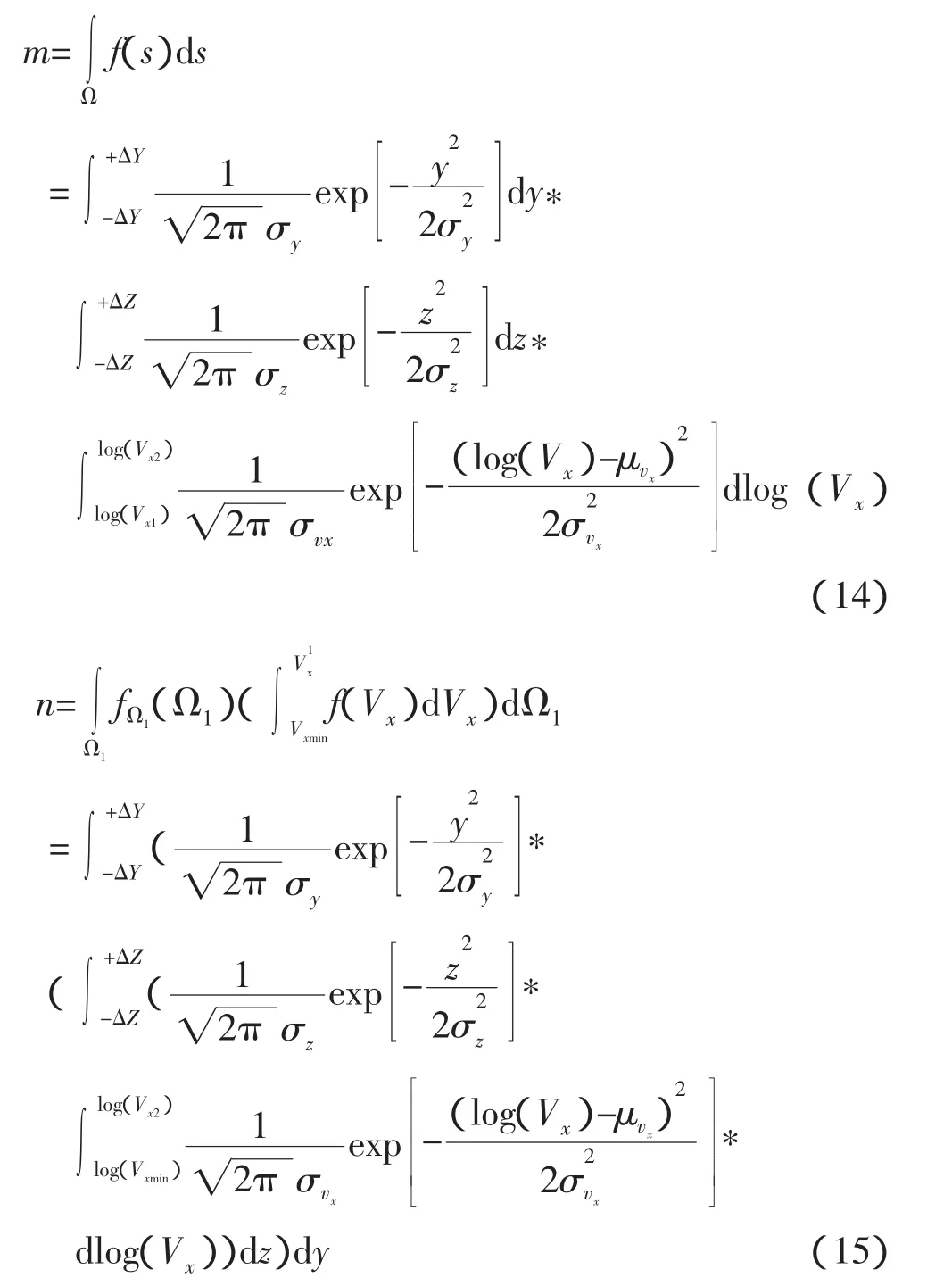
式中：σy=ΔY/3

σz=ΔZ/3

σvx=［log（Vx2）-log（Vx1）］/6

μvx=［log（Vx2）+log（Vx1）］/2

③Y、Z的偏差都服从正态分布，Vx的分布服从均匀分布，此时：

式中：σy=ΔY/3

σz=ΔZ/3

4.2 对接初始条件分布规律对捕获概率的影响

根据上述公式（9）～（17），通过改变对接初始条件，可以得到捕获概率随对接初始条件的变化规律。

以下算例中，Vx、R、Vxmin和CR取值如下：

Vx∈［0，0.35］（m/s）

R∈［0，0.2］（m）

Vxmin=0.04（m/s）

CR=2

横向偏差对捕获概率的影响见图5。

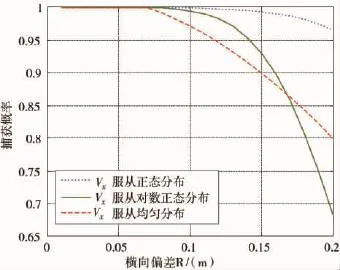
图5 捕获概率随横向偏差R的变化

由图5可知，随着最大横向偏差的逐渐增大，捕获概率逐渐减小。当最大横向偏差在一定范围内时，捕获概率为1，此时，最大横向偏差时能够捕获的最小纵向接近小于Vx1。

在最大横向偏差一定的情况下，捕获概率随着纵向接近速度Vx的分布规律变化而有所不同。若Vx服从正态分布，捕获概率最大，且最大横向偏差的变化对捕获概率的影响最小；若Vx服从对数正态分布，随着最大横向偏差的逐渐增大，捕获概率迅速减小；若Vx服从均匀分布，捕获概率随着最大横向偏差的逐渐增大呈线性减小。

纵向接近速度的下限值Vx1对捕获概率也有影响，见图6。在最大横向偏差不变时，提高两航天器纵向接近速度的下限值，就会提高捕获概率。纵向接近速度服从对数正态分布时，增大纵向接近速度的下限值，可以大幅度地提高捕获概率值。

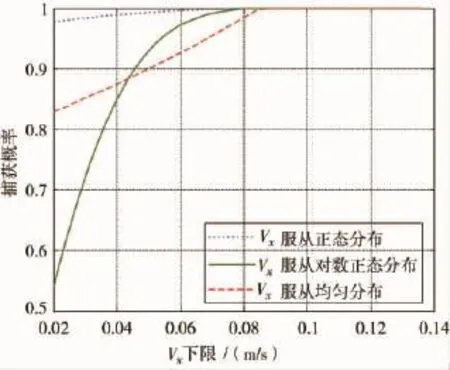
图6 捕获概率随Vx下限的变化

若保持纵向接近速度的范围不变，提高纵向速度的中间值，也可以提高捕获概率，见图7。

在最大横向偏差一定的情况下，对于不同的，捕获概率也不同。图8为V服从不同分布规x律时，捕获概率随的变化。

当增大时，捕获概率减小。若Vx服从正态分布，捕获概率最大，且的变化对捕获概率的影响最小；若Vx服从对数正态分布，随着的逐渐增大，捕获概率迅速减小；若Vx服从均匀分布，捕获概率随着的逐渐增大呈线性减小。

图7 捕获概率随Vx中间值的变化

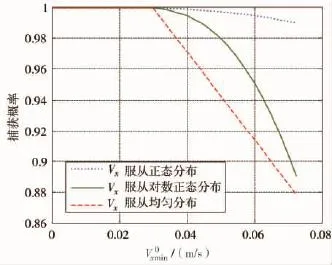
图8 捕获概率随的变化

为确保捕获易于实现，两航天器对接时，需要启动追踪航天器的正推发动机，从而减小纵向速度的下限值，提高两航天器的捕获成功概率。

纵向接近速度的上限值Vx2对捕获概率也有影响，见图9。在最大横向偏差不变时，增大两航天器纵向接近速度的上限值，也会提高捕获概率。若其它条件一样，纵向接近速度服从正态分布时，捕获概率最大。

由于受对接机构的结构尺寸、重量以及航天器对对接过程中的过载等限制，决定了纵向速度的上限值必须在一个合理的范围内，即纵向速度的上限值不能超过对接机构设计的允许值。

综上表明，要提高捕获概率，应采取以下措施：

a.尽量降低两航天器对接时的初始条件偏差；

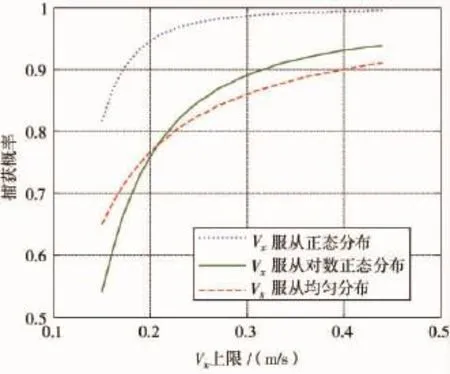
图9 捕获概率随Vx上限的变化

b.提高两航天器间的纵向接近速度；

c.优化纵向接近速度的实现方案，尽量使纵向接近速度的分布规律服从正态分布。

对接时，若还存在其它方向的初始条件偏差，其对捕获概率的影响规律趋势与横向偏差对捕获概率的影响是一致的，在此不再赘述。

5 结论

本文根据对接初始条件分布函数以及对接机构对接捕获的实现方案，建立了捕获概率的计算模型，重点研究了横向偏差和纵向接近速度对捕获概率的影响规律，分析了对接初始条件分布范围及其规律对捕获概率的影响，确定了提高捕获成功概率的方向，可供工程研制参考。而对接时存在多个方向的初始条件偏差及偏差组合，实际的捕获概率模型将更为复杂。◇

［1］娄汉文，曲广吉，刘济生等译.空间对接机构［M］.北京：航空工业出版社，1992，1.

［2］朱仁璋.航天器交会对接技术［M］.北京：国防工业出版社，2007.

［3］张崇峰，覃黎洋.空间对接与空间站［J］.科学，2012，01.

［4］张崇峰.空间对接机构综述［J］.世界科学，2003，01.

［5］陈宝东，郑云青，邵济明等；对接机构分系统研制［J］.上海航天，2011，06.

［6］盛骤，谢式千，潘承毅.概率论与数理统计［M］.第2版.北京:高等教育出版社，1989，81.