考虑收发机损耗的多小区多用户下行链路波束成形算法

夏灿锋，何世文,2，黄永明,3，王海明,2，杨绿溪

（1. 东南大学 信息科学与工程学院，江苏 南京 210096; 2. 东南大学 毫米波国家重点实验室，江苏 南京 210096;3. 上海交通大学 系统控制与信息处理教育部重点实验室，上海 200240）

1 引言

近年来，作为一种能够显著提升系统容量及改善通信质量的强有技术，多输入多输出（MIMO,multiple input multiple output）技术受到了工业界、学术界的广泛关注且得到了深入的研究，但现有文献主要集中于不存在收发机损耗的理想情况下如何设计高效的无线通信传输技术，如多用户MIMO技术、波束成形传输技术等[1～8]。

实际无线通信系统中的收发机存在许多硬件损耗，比如非线性放大器[9]、载频和采样率偏移[10]、IQ 不平衡[11]、相位噪声[12]等。这些损耗对系统性能的影响可以采取一定措施来减少，比如可以通过发射端校准或预失真来补偿，也可以在接收端进行复杂的技术来补偿，如对相位噪声可以采用最大似然估计方法，对于 IQ不平衡有基于前导的估计和削弱方法等。文献[13]中对射频端损耗和相应的各种补偿技术进行了综合的概括。文献[14,15]对收发机补偿后的剩余损耗进行深入研究，并且证明了传统补偿方式后的收发机残留损耗可以较好地建模成一个加性高斯分量，且它的能量随着发射信号的功率增加而增加。

在实际场景，这些补偿方法无法完全消除上述不理想损耗对通信系统性能的影响，即实际无线通信系统依然会残留各种收发机损耗。研究表明这些收发机残留损耗对于低频谱效率的单用户通信系统的影响相对较小，但对于多小区多用户多输入多输出通信系统，这些收发机损耗会对通信系统性能产生严重的影响，进而导致性能急剧下降[16～20]。文献[16]研究了收发机残余损耗对信道容量和误比特率的影响，文中证明了这些残余损耗会严重削弱 MIMO系统最优检测算法的性能；文献[17]研究表明MIMO系统的信道容量受收发机损耗的影响且存在一个上界，从而使传统的复用增益为零；文献[18]理论上分析了非线性损耗对OFDM系统的影响并提出了一种错误率估计方法；文献[19,20]分析了射频器件损伤对高速率和高频谱率系统的影响，并且得出结论需要使用 EVM(error vector magnitude)低于某一特定值的射频器件才能达到性能指标等。然而这些相关文献只是分析了收发机损耗和其对系统性能产生的影响，并没有给出可行的考虑这些残留收发机损耗波束成形的方案。

本文将在现有收发机损耗的模型基础上进一步分析硬件收发机残留损耗对多小区多用户波束成形的影响，进而设计考虑收发机损耗的多小区多用户MIMO下行链路波束成形算法，其研究系统性能优化指标为：

（P1）最小化最差用户均方误差(MSE)；

（P2）最小所有用户的均方误差(MSE)总和。

针对上述2个优化目标，本文提出了2种考虑收发机损耗的多小区多用户MIMO下行链路波束成形算法，数值仿真验证了所提算法的有效性，而且仿真表明相比于传统多小区多用户MIMO下行链路波束成形算法而言，所提算法能够明显地提高系统性能增益。最后将结合本文所提算法的性能提升和算法开销来权衡分析不同损耗场景的选择策略。

2 系统模型

考虑由N小区组成的多小区协同波束下行链路系统，其中每个小区由一个多天线基站和K个单天线用户组成。为了简单起见，不妨假设每个基站均有tN根天线，每个基站只给本小区的用户发送数据且对其他小区用户产生一定的小区间干扰，即本文将重点研究多小区协作波束成形算法优化问题。这样，第 i个小区j个用户的接收信号为

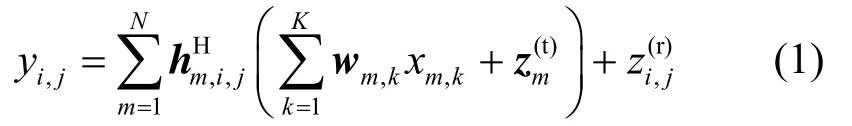
虽然通过收发机均衡及补偿技术可以减少硬件对系统性能的影响，但不能完全消除收发机损耗对系统性能，尤其是MIMO系统的性能的影响。这些收发机残留损耗的影响可以合理地模拟成加性高斯分量，且它的能量随着有用信号能量的增长而增长[18,19]。令发射机残留损耗满足 zm(t)=CNt×1，这样假设是合理的，因为根据大数定理可以证明，收发机的很多残留损耗总和起来可以合理地表示成高斯模型。从发射机射频指标误差向量幅度(EVM,error vector magnitude)的数据仿真曲线可以发现发射机损耗随着发射功率呈一定的单调增长趋势，如图 1所示(场景：LTE power amplifier HXG-122+using 64-QAM waveforms and a state-of-the-art signal generator[16])。

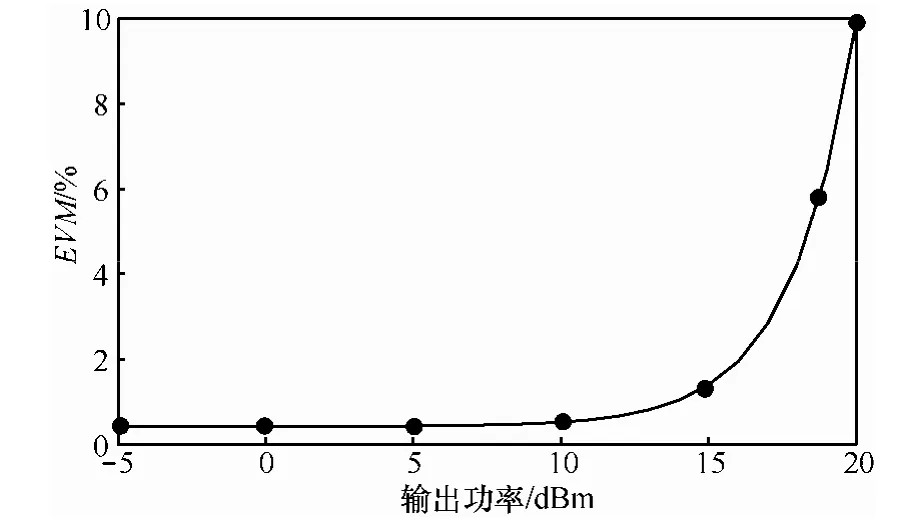
图1 EVM随输出功率曲线

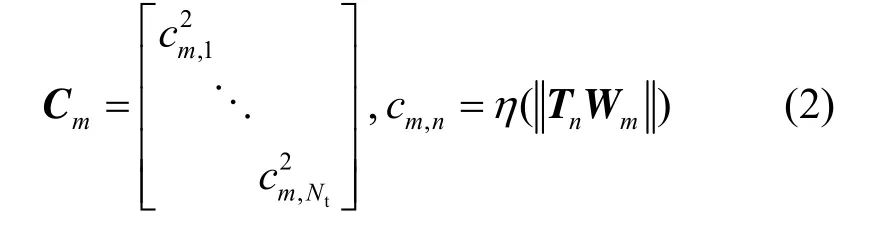
Tn用于取出第n根天线的发射幅度，它是对角阵（在对角线上第n个元素为1，其余位置为0），η(⋅)为关于发射信号幅度的单调递增函数，用来对模拟发射端的损耗特性，它的具体表达式可以通过射频端的EVM特性来测。根据EVM的定义[21]可得

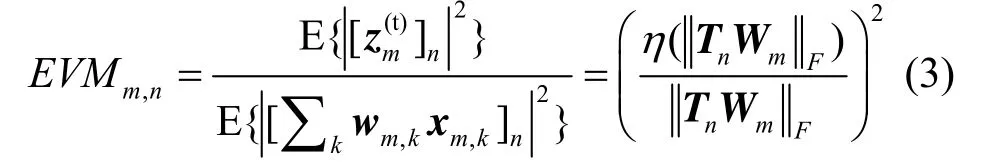
通过对射频端 EVM 测量数据建模可以得到η(⋅)函数为

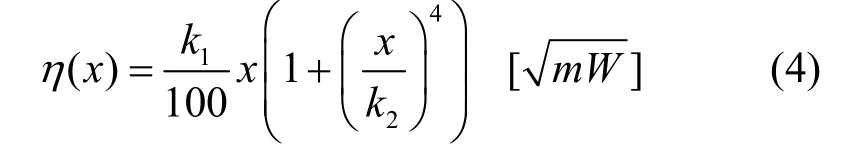
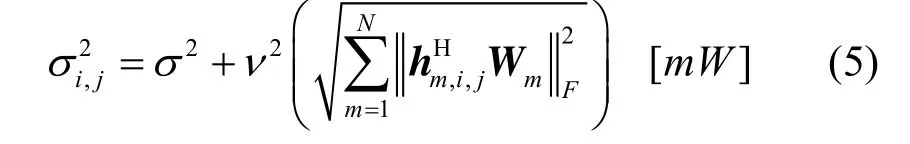
其中，系数k3100为相应的发射端EVM值。

3 波束成形优化算法

本文主要研究基于MSE性能准则的2种优化目标：(P1)最小化最差用户的 MSE，即最小化最大MSE问题；(P2)最小所有用户的MSE之和。而且，针对这2个优化问题，将提出2种考虑收发机损耗的多小区多用户的下行链路波束成形算法，并数值仿真验证所提算法的有效性且分析系统改善程度。

3.1 均方误差(MSE)性能准则

由第2节的系统模型可知，用户发送数据 xi,j、发射机损耗 zm

(t)，接收机损耗 zi(,rj)的分布分别为三者相互独立，因此可以得到式(7)中的各项分式的表达式可以表示为

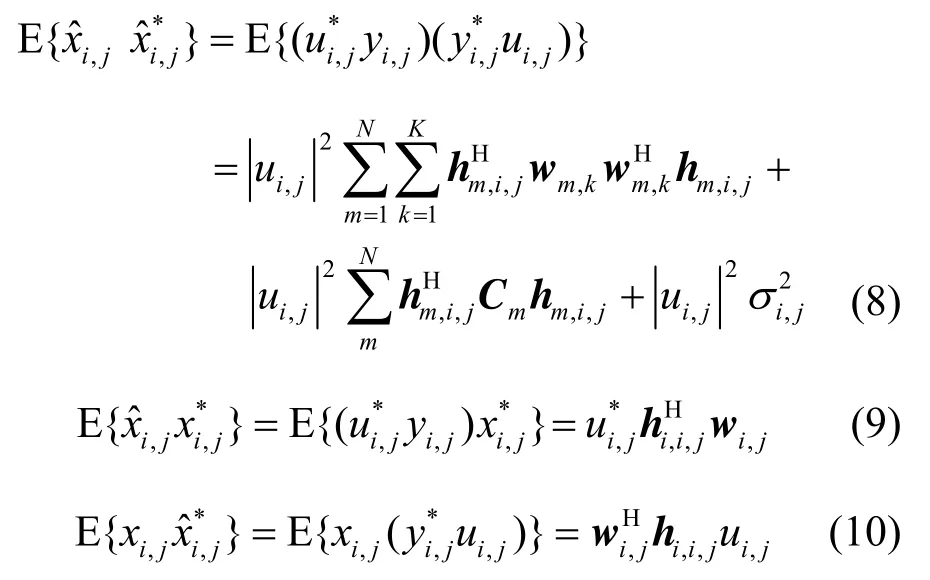
将式(8)～式(10)代入式(7)可得 M SEi,j表达式为且

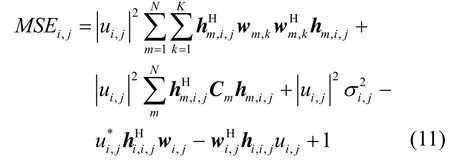
为了同时研究用户间的公正性及系统的整体性能，本文主要研究以MSE为准则的2个优化问题，其一是研究用户间的公正性的最小化最大用户MSE，即

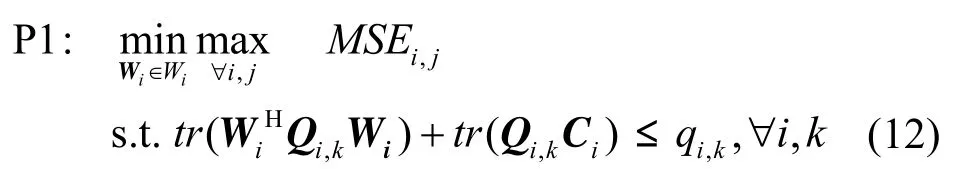
其二是研究系统整体性能，即最小化系统均方差误之和，即

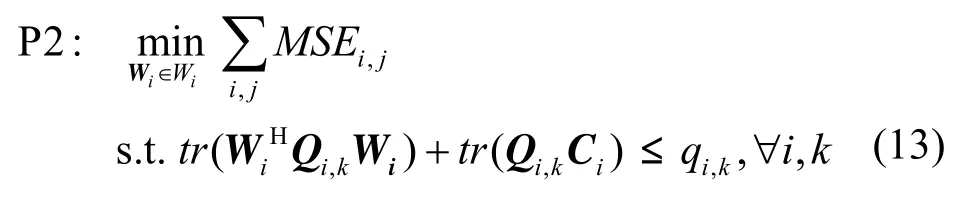
其中，式(12)和式(13)中的约束条件是对功率的约束，是半正定矩阵且这是为了对各个空间方向的功率进行限制。对于第i个小区j个用户而言，其功率受到的限制条件数为Li，这个数目和限制条件的情况有关：当系统采用总功率限制时，则；当系统采用每根天线功率限制时，则 Qi,k表示第 i个小区基站的功率限制条件，且第 k个对角线元素非零，即，其中，集合 Wi是满足功率约束条件的有效波束集合，即

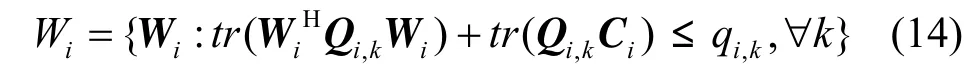
定理1 在信道环境 hm,i,j和波束矩阵 wm,k已知的前提下，使第i小区第j用户的均方误差 M SEi,j最小的接收端均衡系数为

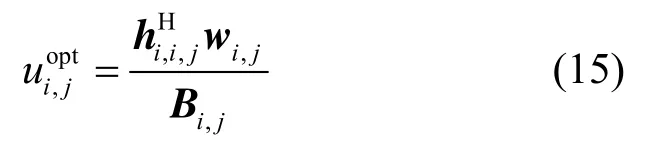
其中，

证明 从优化问题P1和P2的最小化目标、拉格朗日KKT条件及将式(11)对,iju*求导即可得

其中，

3.2 算法的描述

由于优化问题P1和P2的优化变量iW和,iju 相互耦合，致使优化问题直接求解变得十分复杂，这里设计分层优化迭代算法求解原始优化问题：即先固定其中一些变化变量，然后优化求解其他优化变量。

3.2.1 优化目标P1重构

引入辅助变量,mnt 、,ijr，将优化问题P1转化为如下形式

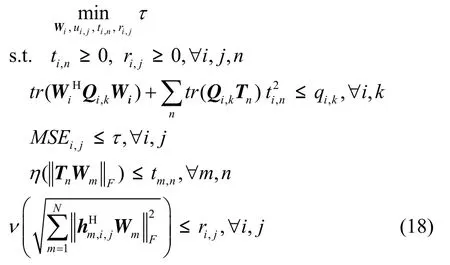
现有文献研究表明函数η(⋅)和ν(⋅)通常是凸函数，因此不失一般性，下面不妨假设这2个函数均为凸函数。这样上述优化问题可以转化成二阶锥规划（SOCP）问题的标准形式， 转化过程中主要是将MSE的表达式写成如下形式：

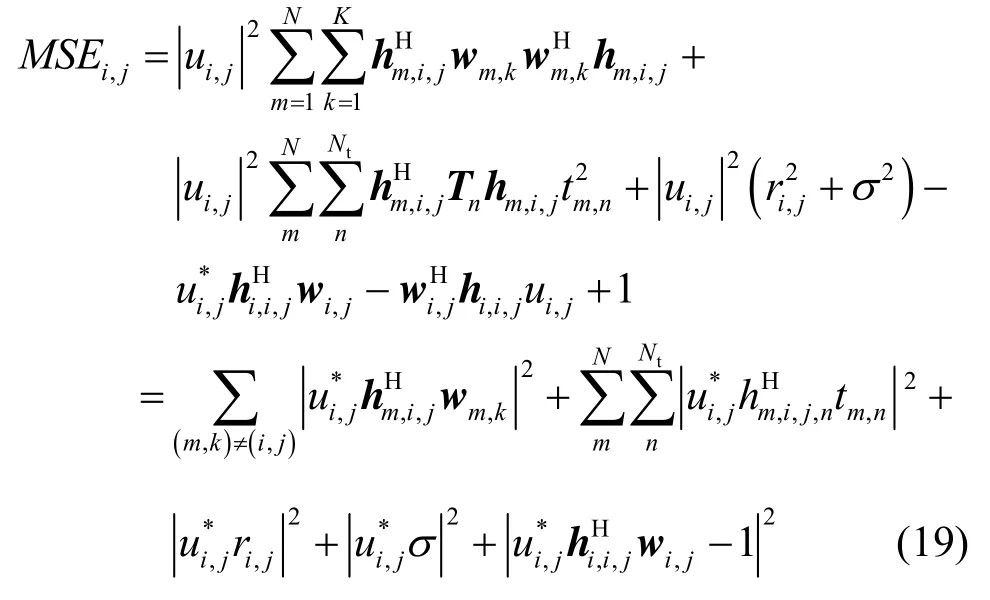
优化问题P1的交替迭代算法如算法1所示，其中τ表示凸优化算法的优化指标，在优化问题(P1)中τ= m ax MSEi,j。阈值δ表示优化目标参数τ更新的收敛程度，当τ更新的差值小于阈值δ时，则认为算法已经收敛。

算法1 优化问题P1的迭代优化算法

1) 初始化最佳接收端权衡系数 U(n)、波束矩阵和τ(n)；

2) 给定 U(n)，优化求解优化问题(18)获得最佳波束矩阵 W(n+1)和优化指标τ(n+1)；

由于算法1的步骤2）和步骤3）的更新过程均最小化目标函数值，进而产生一个单递减序列，实际通信系统中 MSE值是有限值，因此，单有界序列原理可知上述所提算法收敛。

3.2.2 优化目标P2重构

引入发射机损耗变量 tm,n和接收机损耗变量ri,j，优化问题(P2)转化为如下优化问题

如果η(⋅)和ν(⋅)是凸函数，那么上述优化问题可以同样可以转化成 SOCP的标准形式来优化求解。这样，优化问题 P2的交替迭代算法如算法 2所示，其中，λ表示凸优化算法的优化指标，在优化问题(P2)中。阈值δ表示优化目标参数λ更新的收敛程度，当λ更新的差值小于阈值δ以下时，则认为算法已经收敛。

算法2 优化问题P2的迭代优化算法

1) 初始化最佳接收端权衡系数 U(n)、波束矩阵和 λ(n)；

2) 给定 U(n)，优化求解优化问题(20)获得最佳波束矩阵 W(n+1)和优化指标 λ(n+1)；

类似于所提算法 1，上述优化算法的收敛仍然可由单调有界序列原理得以保证。

4 仿真

本节将本文提出的考虑收发机损耗的多小区多用户下行链路波束成形算法性能进行仿真。考虑仿真场景为3个小区，每个小区2个用户，每个基站4天线的情况（N=3，K=2，Nt=4），接收端用户只一根天线，基站每根天线20 dBm的功率限制，其他情况可推广。仿真的场景如图2所示，3个相邻小区的中心各放置一个基站，且基站间距离为500 m。这里只考虑相邻小区有重叠覆盖区域的扇形覆盖区域里用户的性能，如图 2所示阴影区域，这个区域的用户受相邻小区干扰最为明显，其他区域可类似考虑。用户均匀随机分布在基站覆盖区域内，且距离基站至少35 m。系统的仿真参数如表1所示，这个仿真系统是3GPP LTE标准中场景1的版本，同时假设是不相关的瑞利衰落信道和独立的阴影衰落。

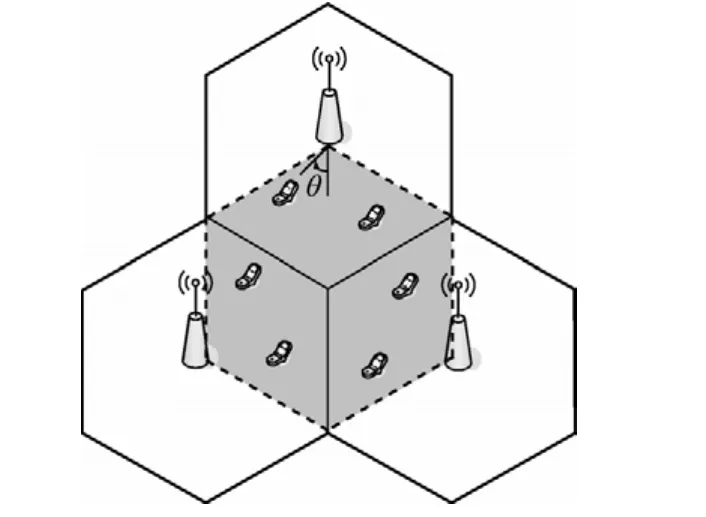
图2 仿真系统场景

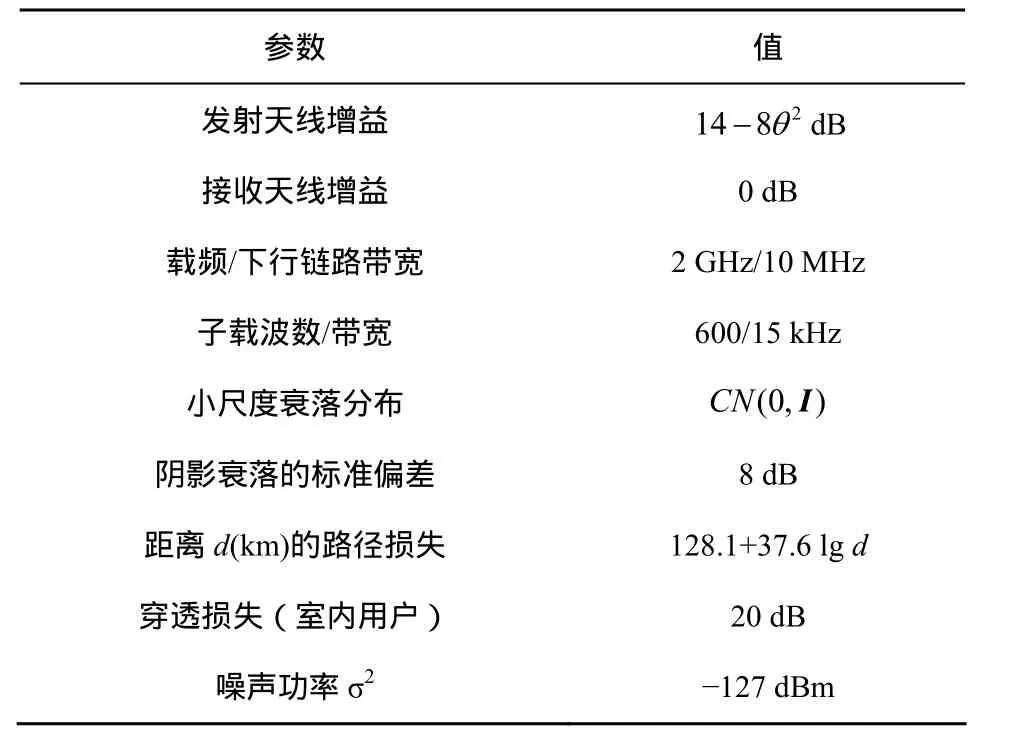
表1 仿真场景中的仿真参数

在该场景下，对优化目标函数(P1)和优化目标函数(P2)分别进行了仿真，同时为了对比，计算了只采用传统补偿技术而没有考虑收发机残留损耗的优化算法，即在优化时令收发机残留损耗为 0（k1=0，k2=+∞，k3=0），得出传统收发机情况下的波束成形，然后代入实际场景中计算得其相应的损耗影响。事实上不考虑残留损耗的波束成形优化算法中，系统会给用户分配更多的信号能量用于满足用户 MSE要求，然而这在实际硬件系统中，过高的发射能量会增加收发机损耗从而反过来影响系统性能。

图3和图4分别表示波束成形优化算法P1和P2的收敛情况，其中选择参数（k1=5，k2=6，k3=2），随机选取几组信道对 2种算法的迭代效果进行仿真，从仿真结果图中可以看到，2种算法的收敛效果良好。同时可以统计，为达到同样的收敛效果，优化算法P1的平均迭代次数略小于优化算法P2；而就MSE优化的性能而言，优化算法P2的最终用户MSE会略低于优化算法P1，可见2种算法存在收敛性能和MSE优化性能的权衡折中。

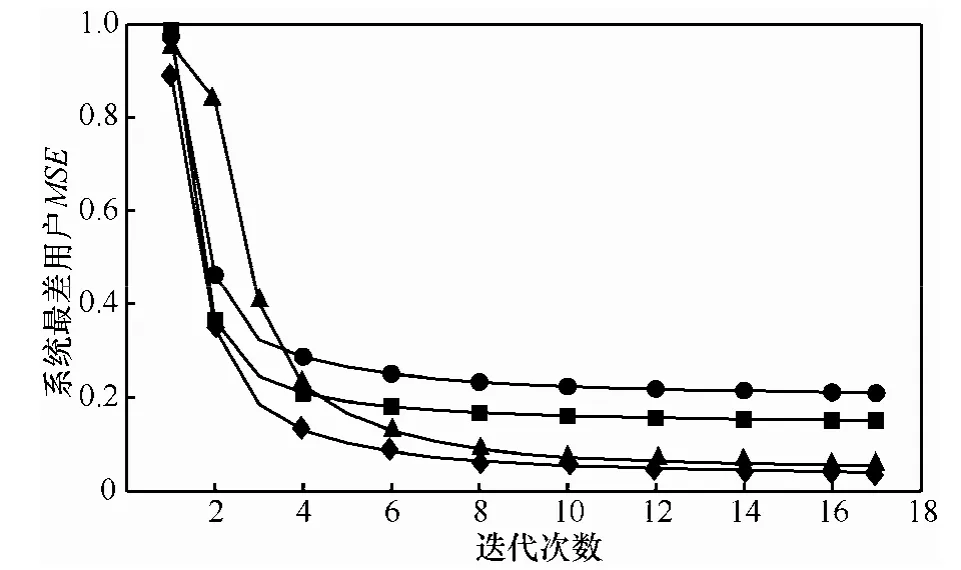
图3 优化方案P1迭代次数(k1=5, k2=6, k3=2)

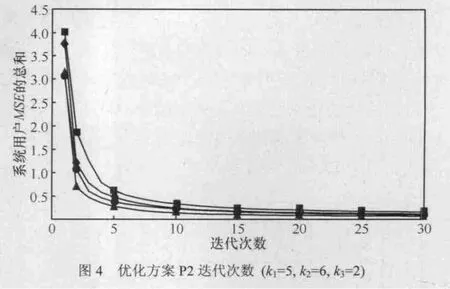
图4 优化方案P2迭代次数 (k1=5, k2=6, k3=2)

图5 ～图7分别给出了所提优化问题P1的优化算法性能仿真曲线，其中，图5表示系统平均最差用户MSE随k1的变化趋势(k3=2, δ=0.005)；图6表示系统平均最差用户MSE随k3的变化趋势(k2=7，δ=0.005)；图7表示系统平均最差用户MSE随k1、k3的变化趋势(δ=0.005)。

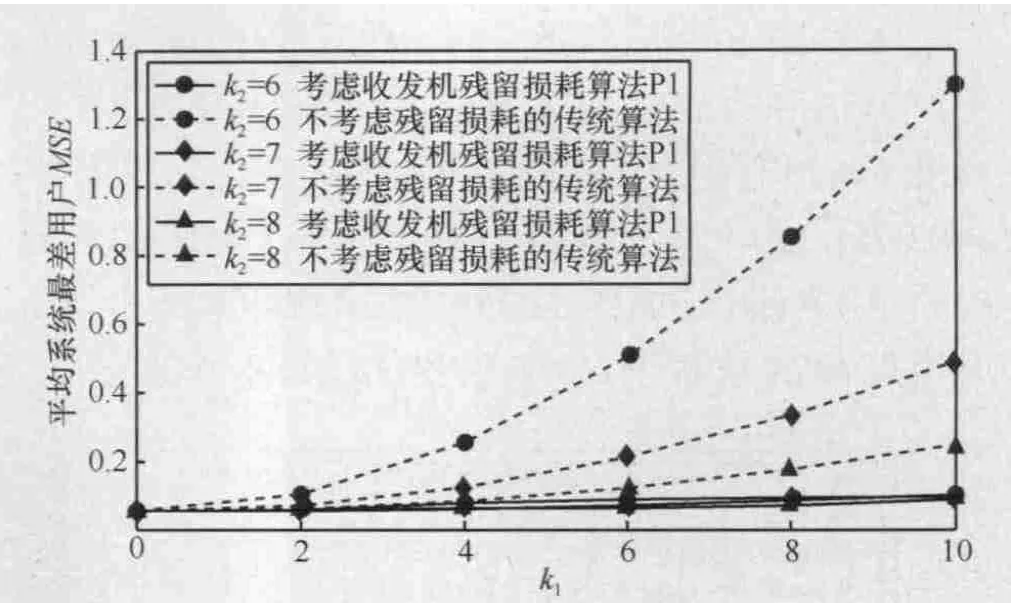
图5 系统平均最差用户MSE随k1的变化趋势（k3=2,δ=0.005）

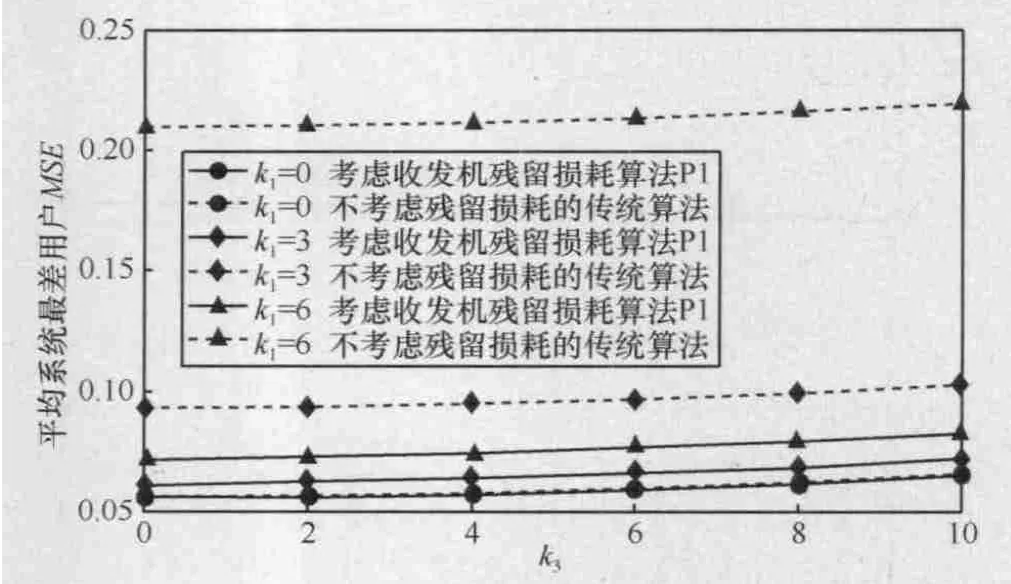
图6 系统平均最差用户MSE随k3的变化趋势(k2=7, δ=0.005)

图5 ～图 7中实线表示的是考虑收发机残留损耗的优化算法P1的性能，虚线表示的是未考虑残留损耗的传统优化算法性能。从图5～图7中可以发现，对于传统优化算法，收发机残留损耗对系统性能产生严重的影响，随着k1增大、k2减少，根据式(4)，收发机的损耗逐渐变大，系统的性能下降，系统平均最差用户的MSE随着变大。而提出的考虑损耗的优化方案P1能有效地将MSE控制在一个比较低的范围内，比未考虑损耗的仿真结果有了明显改善。随着k1减少，k2增加，2种方案的性能差距逐渐变小，只有当损耗系数k1在2以下时两者的相差才比较小。

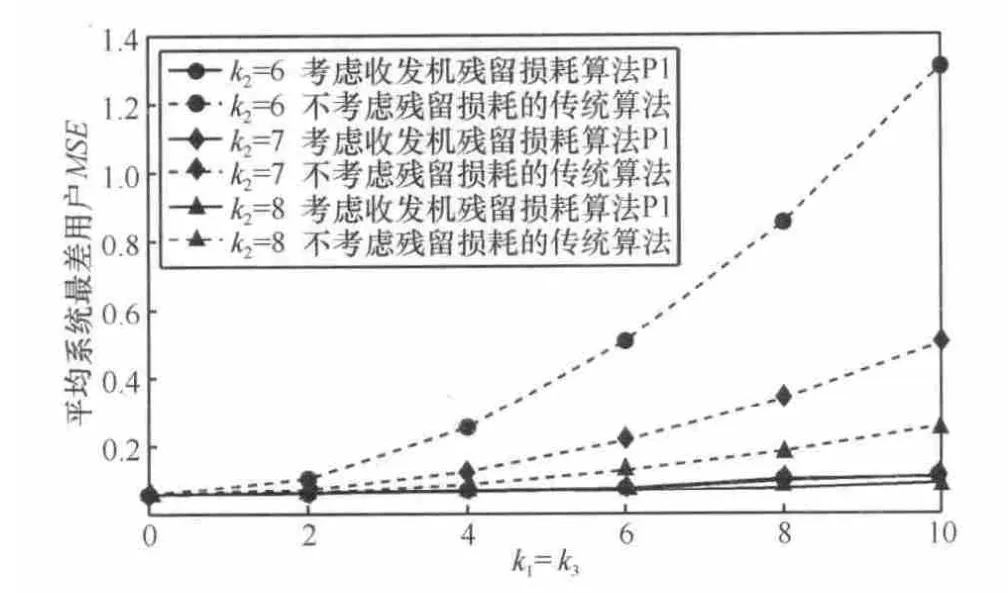
图7 系统平均最差用户随k1、k3的变化趋势(δ=0.005)

图8 ～图10表示的是采用优化算法(P2)后系统总用户MSE和随k1、k2和k3变化的趋势。其中图8表示系统平均所有用户 MSE总和随k1的变化趋势(k3=2,δ=0.005)；图9表示系统平均所有用户MSE总和随k3的变化趋势(k2=7, δ=0.005)；图10表示系统平均所有用户MSE总和随k1、k3的变化趋势(δ=0.005)。

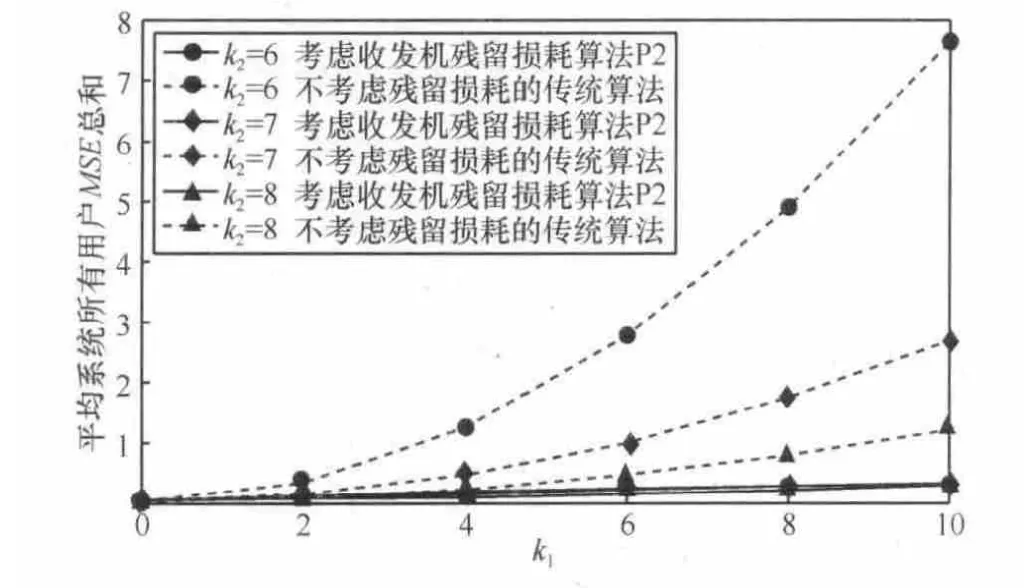
图8 系统所有用户MSE总和随k1的变化趋势(k3=2, δ=0.005)

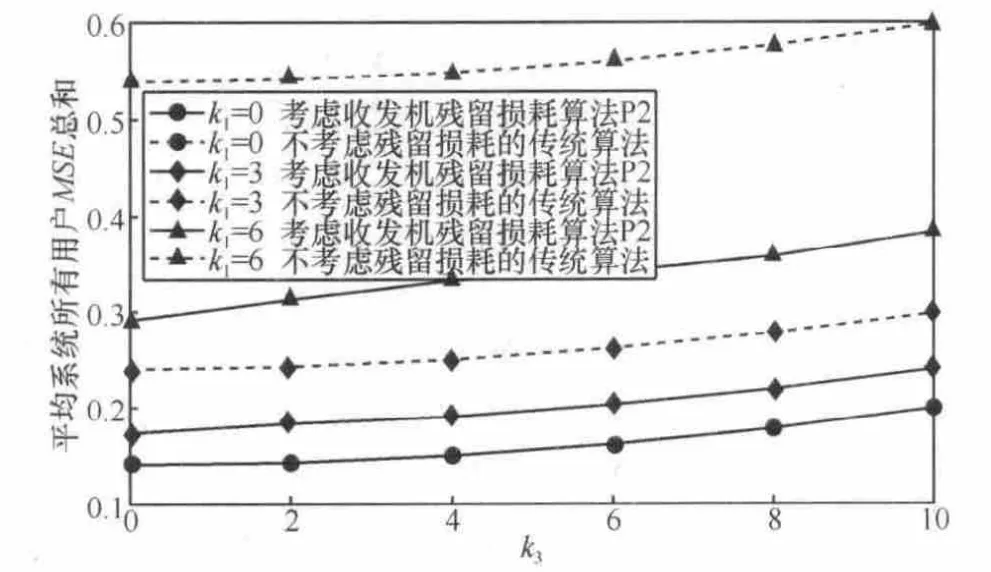
图9 系统所有用户MSE总和随k3的变化趋势(k2=7, δ=0.005)

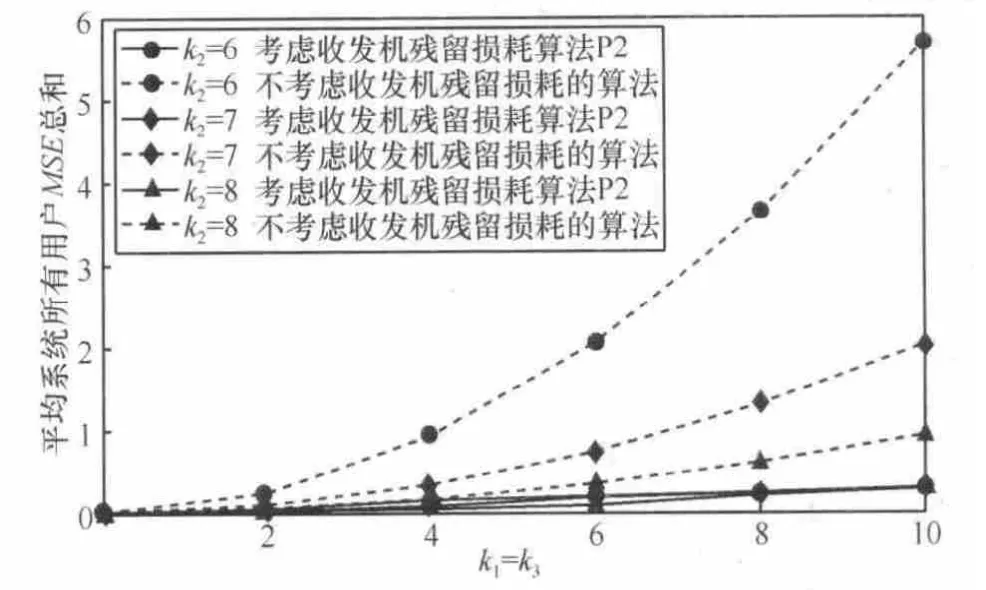
图10 系统所有用户MSE总和随k1、k3的变化趋势(δ=0.005)

图8 ～图10中实线表示的是考虑收发机残留损耗的优化算法 P2的性能，虚线表示的是未考虑残留损耗的传统优化算法性能。从图8～图10中可以看到，对于传统优化算法，收发机损耗对系统性能产生了严重影响，随着k1增加、k2减小，k3增加，系统收发机的损耗逐渐增加，用户的 MSE总和呈上升趋势。同时，考虑损耗的优化算法 P2比未考虑损耗的优化算法的性能有明显的提升，能够有效地将收发机损耗的影响控制在一个比较小范围内。当 k1趋向于0，k2趋向于无穷大，k3趋向于0（即损耗减小）时，两者的性能差距才逐渐减小。

为了进一步研究协同算法对小区边缘用户的性能影响，图11给出了协同算法对小区边缘用户性能曲线，其中用户随机分布在离基站250 m以外。从图11中可以看到算法对小区边缘用户场景，本文提出的优化算法相对于传统算法能有效地将系统最差用户的MSE控制在较低的范围内，性能上有更明显的提升。当k1＜2时，2种算法体现出来的性能接近，而随着k1增大，k2减小，系统收发机残留损耗变大，本文所提算法的性能优势更加明显。对于传统算法，系统性能随损耗系数k1的变化比k2明显。

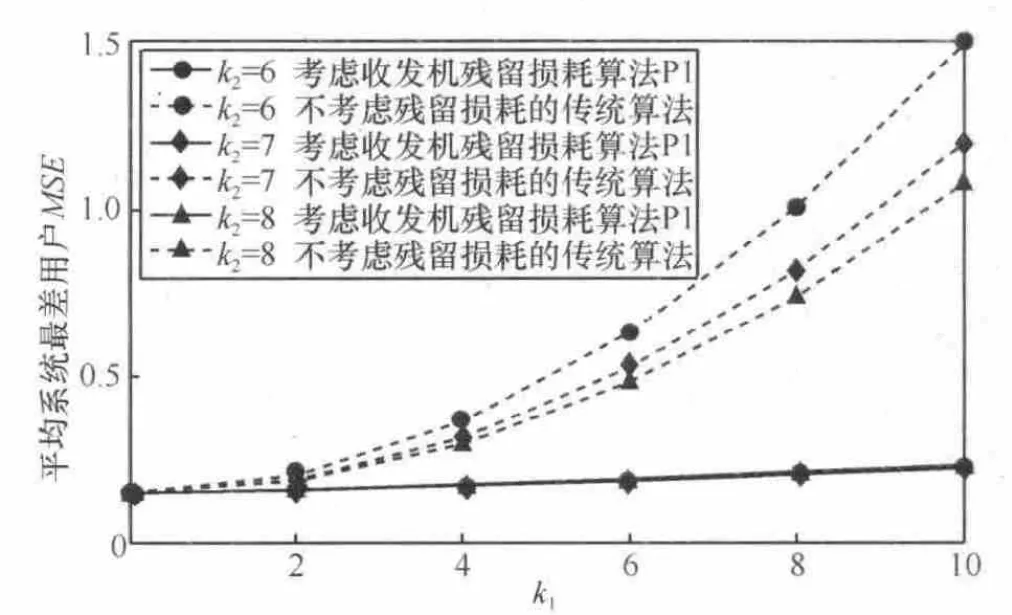
图11 小区边缘用户系统平均最差用户MSE随k1的变化趋势（k3=2, δ=0.005）

从算法复杂度考虑，本文提出的算法相对于未考虑收发机残留损耗的算法其约束条件和变量增加了，又因为SOCP算法复杂度随着求解变量和约束条件数目呈正相关[25,26]，因而本文所提考虑收发机残留损耗的优化算法在提升系统性能的同时也增加了一定复杂度，2种算法的开销主要由交替迭代次数和每次求解SCOP问题所消耗的时间。图12对考虑收发机残留损耗的优化算法P1与传统算法进行性能提升和平均时间开销的仿真分析，其中本仿真采用的计算机配置为：处理器型号为Intel(R) Xeon(R)CPU W3550@3.07 GHz，内存为3.48 GB，操作系统为32 bit WIN7操作系统，仿真次数为2 000次。

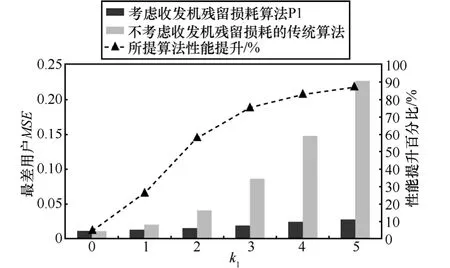
(a) 性能提升变化趋势

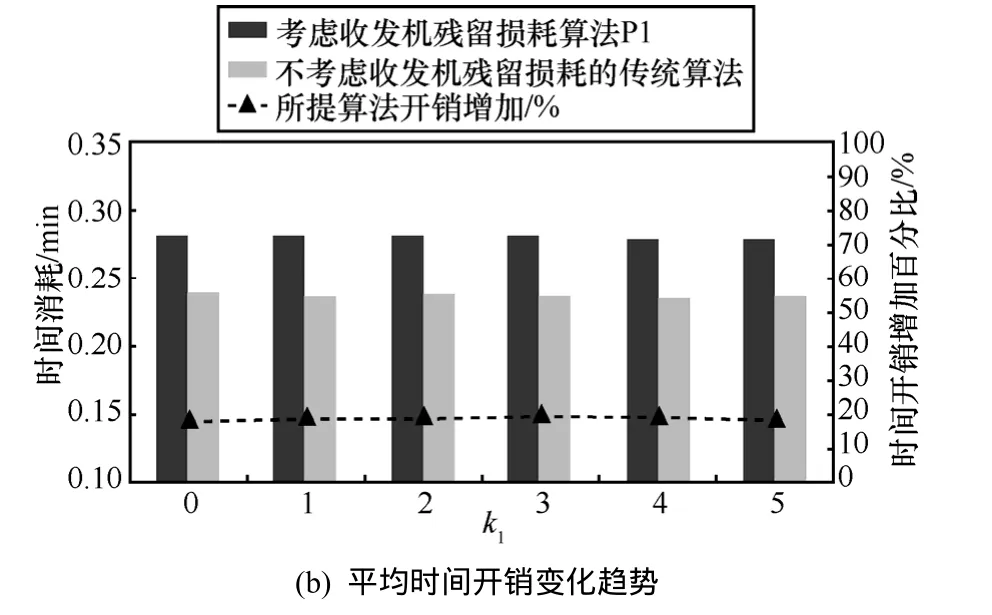
图12 考虑收发机残留损耗算法P1和未考虑残留损耗的传统算法性能提升与平均时间开销分析(k2=7, k3=3,δ=0.005)

从图 12分析可得，随着收发机残留损耗的增加，相对于传统算法，考虑残留损耗的优化算法的性能提升百分比逐渐增加，而算法平均运行时间开销几乎不变，即平均时间开销增加约为19%。对比图12(a)性能提升百分比曲线和图12(b)时间开销百分比曲线可以发现，当k1＜0.7时，本文所提算法P1所带来的性能提升百分比小于时间开销所增加的百分比，此时适用传统算法；当k1＞0.7时，本文所提算法 P1性能提升百分比大于时间开销所增加的百分比，此时适用本文提出的优化算法。其他损耗系数场景可做类似分析。因而实际应用时，可以根据硬件器件的损耗系数并结合性能提升与实际时间开销的权衡来判断本文提出的考虑收发机残留损耗的优化算法和传统算法的选择策略。

5 结束语

实际硬件系统存在收发机损耗，虽然通过传统的发射机和接收机补偿技术可以一定程度减少，但残留的收发机损耗仍然会对系统产生很大的影响。为进一步减少残留损耗影响，本文分析了残留收发机损耗的模型，并设计了考虑收发机损耗的多小区多用户下行链路波束成形算法，主要考虑 2个指标：(P1)使系统最差用户MSE最小准则，(P2)使系统所有用户的MSE总和最小准则，采用了凸优化算法和迭代算法进行分析。从MATAB仿真结果可以看出，本文提出的考虑收发机损耗的优化算法相对于传统未考虑收发机残留损耗的优化算法在性能上有了很大的提升。最后，本文从性能提升和算法开销增加角度分析了如何权衡使用本文提出的优化算法。

[1] RASHID F, LIU K, TASSIULAS L. Transmit beamforming and power control for cellular wireless system[J]. IEEE J Sel Areas Commun,1998, 16(8)∶1437-1450.

[2] DAHROUJ H, YU W. Coordinated beamforming for the multicell multi-antenna wireless system[J]. IEEE Trans Wireless Commun, 2010,9(5)∶ 1748-1759.

[3] VENTURINO L, PRASAD N, WANG X. Coordinated linear beamforming in downlink multicell wireless networks[J]. IEEE Trans Wireless Commun, 2010, 9(4)∶1451-1461.

[4] BJORNSON E, JALD´EN N, BENGTSSON M. Optimality properties,distributed strategies, and measurement based evaluation of coordinated multicell OFDMA transmission[J]. IEEE Trans Signal Process, 2011, 59(12)∶6086-6101.

[5] HUANG Y M, XU D F, YANG L X. A limited feedback precoding system with hierarchical codebook and linear receiver[J]. IEEE Transactions on Wireless Communications, 2008,7(2)∶4843-4848.

[6] HUANG Y M, ZHENG G, BENGTSSON M. Distributed multicell beamforming design with limited intercell coordination[J]. IEEE Transactions on Signal Processing, 2008, 7(12)∶728-738.

[7] HE S W, HUANG Y M, YANG L X. A multi-cell beamforming design by uplink-downlink max-min SINR duality[J]. IEEE Transactions on Wireless Communications, 2012, 11(8)∶2858-2867.

[8] HUANG Y M, YANG L X, BENGTSSON M. Exploiting long-term channel correlation in limited feedback SDMA through channel phase codebook[J]. IEEE Transactions on Signal Processing, 2011, 59(3)∶1217-1228.

[9] SANTELLA G, MAZZENGA F. A hybrid analytical-simulation procedure for performance evaluation in M-QAM-OFDM schemes in presence of nonlinear distortions[J]. IEEE Trans on Vehicular Technology, 1998, 47(1)∶142-151.

[10] SPETH M, FECHTEL S A, FOCK G. Optimum receiver design for wireless broad-band systems using OFDM-Part I[J]. IEEE Trans Comm, 1999, 47(11)∶1668-1677.

[11] SCHENK T C W, FLEDDERUS E R, SMULDERS P F M.Performance analysis of zero-IF MIMO OFDM transceivers with IQ imbalance[J]. Journal of Comm, 2007, 2(7)∶9-19.

[12] SCHENK T, TAO X J, SMULDERS P. Influence and suppression of phase noise in multi-antenna OFDM[A]. Proc IEEE VTC 2004-Fall[C].Los Angeles, USA, 2004.1443-1447.

[13] SCHENK T. RF Imperfections in High-rate Wireless Systems∶ Impact and Digital Compensation[M]. Germany∶ Springer, 2008.

[14] KOCH T, LAPIDOTH A, SOTIRIADIS P. Channels that heat up[J].IEEE Trans Inf Theory, 2009, 55(8)∶ 3594-3612.

[15] MOGHADAM N, ZETTERBERG P, HJALMARSSON H. Correlation of distortion noise between the branches of MIMO transmit antenna[A].Proc IEEE PIMRC[C]. Sydney, Australia, 2012.2079-2084.

[16] STUDER C, WENK M, BURG A. MIMO transmission with residual transmit-RF impairments[A]. Proc ITG/IEEE WSA[C]. Bremen,Germany, 2010.189-196.

[17] BJORNSON E, ZETTERBERG P, BENGTSSON M. Capacity limits and multiplexing gains of MIMO channels with transceiver impairments[J]. IEEE Communications Letters, 2012,17(1)∶1-4.

[18] DARDARI D, TRALLI V, VACCARI A. A theoretical characterization of nonlinear distortion effects in OFDM systems[J]. IEEE Trans Commun, 2000, 48(10)∶1755-1764.

[19] GALIOTTO C, HUANG Y, MARCHETTI N. Performance evaluation of non-ideal RF transmitter in LTE/LTE-advanced systems[A]. Proc European Wireless[C]. Aalborg, Denmark, 2009.266-270.

[20] LTE performance vs output power, model∶ HXG-122+mini-circuits[EB/OL].http∶ //www.minicircuits.com/app/AN60-050.pdf.

[21] HOLMA H, TOSKALA A. LTE for UMTS∶ Evolution to LTE-Advanced[M]. America∶ Wiley, 2011.

[22] BREHMER J, UTSCHICK W. Optimal interference management in multi-antenna, multi-cell systems[A]. Proc Int Zurich Seminar on Commun[C]. Zurich, Switzerland, 2010.134-137.

[23] 3GPPTS 36.814.Further Advancements for E-UTRA Physical Layer Aspects(Release 9)[S]. 2010.

[24] GRANT M, BOYD S. CVX∶ Matlab software for disciplined convex programming[EB/OL]. http∶// cvxr.com/ cvx, 2011.

[25] NESTEROV Y, NEMIROVSKY A. Interior-Point Polynomial Methods in Convex Programming[M]. Philadelphia∶ Society for Industrial and Applied Mathematics, 1994.

[26] LOBO M, VANDENBERGHE L, BOYD S. Applications of second order cone programming[J]. Linear Algebra APP, 1998, 284(1)∶193-228.