基于CSP的能耗高效云计算资源调度模型与算法

林伟伟，刘波，朱良昌，齐德昱

(1. 华南理工大学 计算机科学与工程学院，广东 广州 510006；2. 华南师范大学 计算机学院，广东 广州 510631)

1 引言

随着云计算技术的发展和云应用的普及，云计算现在已经被越来越多的企业接受，并同时对其展开了广泛的研究[1]。最近几年，随着计算机系统电能消耗的不断增加，能源的高效利用已经成为现代计算机系统(如数据中心和云端)的一个非常重要的研究内容[2]。近期，有一些关于云计算的资源提供与云计算资源管理的研究，其中GARG等[3]提出一种接近最优的调度策略，该策略利用横跨不同数据中心之间的数据为云提供者服务。他们考虑了许多影响能源效率的因素(例如：能源消耗、碳排放速度、工作量、CPU功耗效率)，这些因素依据其位置、结构设计和管理系统的不同而在各个数据中心进行变化。为了解决这一问题，出现了一些基于装箱问题部署虚拟服务器的优化方法，在一些文献中有其具体的描述[4～8]，关于虚拟机的部署问题就被建模为装箱问题。然而，目前提出的面向能耗优化的调度方法大部分是针对同构服务器的调度[7,9～13]，但是，由于现有的数据中心服务器的采购时间不同、使用年限不同及品牌不同等异构性，比如文献[13]描述的数据中心的服务器往往是异构的，因此，目前提出的大部分同构服务器调度方法不能很好地应用在一般的云计算数据中心的能耗管理中。

为此，本文针对异构物理服务器的能耗优化资源调度问题进行研究，利用约束满足问题[14]对异构物理服务器的能耗优化资源调度问题建模，并基于Choco[15]约束编程求解建立的能耗优化资源分配模型，能够减少虚拟化的云数据中心的服务器能源消耗。然后，设计了资源调度算法来实现该优化配置方案。最后，使用Choco模拟实验进行算法评价，实验结果表明提出的模型和算法在能耗方面明显优于已有的资源调度方法。

2 相关研究

减少能源的消耗对于资源供应商减少成本和利润最大化来说非常重要[16,17]。BELOGLAZOV等[18]提出了一种用于虚拟机化云计算数据中心的有效的资源管理系统，它可以减少运营成本并提供所需的服务质量。节约能源是通过虚拟机不断地依据当前的资源利用率以及虚拟机和热状态下的计算节点之间建立的虚拟拓扑网络结构来进行整合的。RODERO等[19]为高性能计算和虚拟化计算平台提出了一种能量感知型的网络配置方法。能源效率的提高是通过工作量的感知，恰到好处地动态配置机制以及通过关闭主机系统中没有映射虚拟机的子系统方法来实现的。ABDELSALAM等[20]创建了一个用于云计算环境，主要服务于客户的如Web服务一样的交互式应用的电力管理数学模型，这个数学模型计算服务器的最优数量和它们应该运行的频率。文献[21]中，作者提出了一个提供高效、绿色、强化的可扩展的云计算架构的新框架。通过使用电力调度技术、可变的资源管理、实时调度和最小化的虚拟机设计等技术，使基于最小化云开销的数据中心系统的整体功效得到了改善，CHANG等[22]对云资源的优化配置进行了研究。他们制定了关于计算能力和其他资源的多样性的资源分配问题。他们提出了一个可证明的在多项式时间内得到接近最优解的近似算法。然而现今的方法大都考虑的是给予的每个物理机节点上有着相同的物理参数，如CPU速度、硬盘容量、内存等。

此外，绝大部分方法仅将处理器作为唯一值得考虑的资源，而抛弃了其他一些同样很重要的资源，例如内存和存储空间。这样就导致由于工作量大量聚集在同一个节点而形成瓶颈，导致性能的下降以及能量消耗的增加，这个在文献[23]中有所提及。在运行时虚拟机实现再分配的能力，可以动态地配制工作量，同时可以使虚拟机实现重新部署，使运行的物理机节点达到最小，而空闲节点则切换为省电模式。然而虚拟机的迁移会导致时间延迟、额外的性能开销以及功耗，所以需要通过仔细分析和智能技术消除这些因工作量变化而导致的非生产性的迁移[2]。

装箱问题是一个著名的NP组合难题，已提出许多启发式和贪心算法来解决这难题[9,24]。一些启发式算法，例如first-fit decreasing (FFD)[10]、best-fit decreasing(BFD)[10]和modified best fit decreasing(MBFD)[25]都被提出来和应用在数据中心的虚拟机调度中[4～8]。这些方法大部分是针对同构服务器的调度，不能很好地应用在一般的异构云计算数据中心的资源调度和能耗管理中。CSP(约束满足问题)[26]：由一个变量集合和一个约束集合组成；问题的一个状态是由对一些或全部变量的一个赋值定义的；问题的解是满足所有约束的完全赋值，或更进一步，使目标函数最大化。约束满足问题作为人工智能研究的一个基本问题，在许多实际问题中都得到了广泛的应用，特别是调度中的资源分配问题。为此，本文主要是针对物理服务器异构的云数据中心的资源调度问题进行研究，给出异构物理服务器环境下的能耗优化的资源调度模型和算法，减少云数据中心的能源消耗。

3 基于CSP的能耗优化资源分配模型

3.1 问题描述

最直观的节能减排方式就是关闭利用率不高的服务器，在传统模式中，一个应用运行在一个服务器上，关闭服务器就等于关闭了应用；然而，服务器虚拟化为解除应用与物理服务器的绑定提供了可能，在负载低谷期，管理员可以将原来运行在各个服务器上的应用整合到较少的几台服务器上，关闭空闲的服务器，已达到绿色节能的目的。因而，一般能耗中的优化问题就是最小化物理主机数；但是，在考虑物理主机异构的情况，由于每个物理主机都有不同能耗，此时，能耗优化的问题并不是最小物理主机数。下面举个例子进行具体说明。

物理服务器和虚拟机的资源大小及能耗参数如图1所示，其中Dy1～3表示当虚拟机VM1～3分配到该物理节点时产生的动态能耗。待部署的虚拟机以及其参数如图2所示。假设需要将这3台虚拟机部署在这3个物理节点上。如果采用最小主机数策略，3台物理机都应该分配到PM1上，这时的总能耗为650 W；若将VM1和VM2部署在PM2上，VM3部署在PM3上，则总能耗为420 W，可见，在物理主机异构的情况下，能耗的优化问题并不是最小物理主机数，而是综合能耗最小。针对上述问题，本文提出了一个基于CSP的能耗优化的云资源调度框架，该框架的系统架构如图2所示。

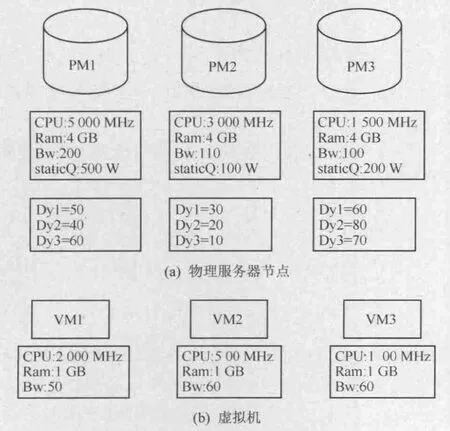
图1 物理服务器与虚拟机的资源大小及能耗参数

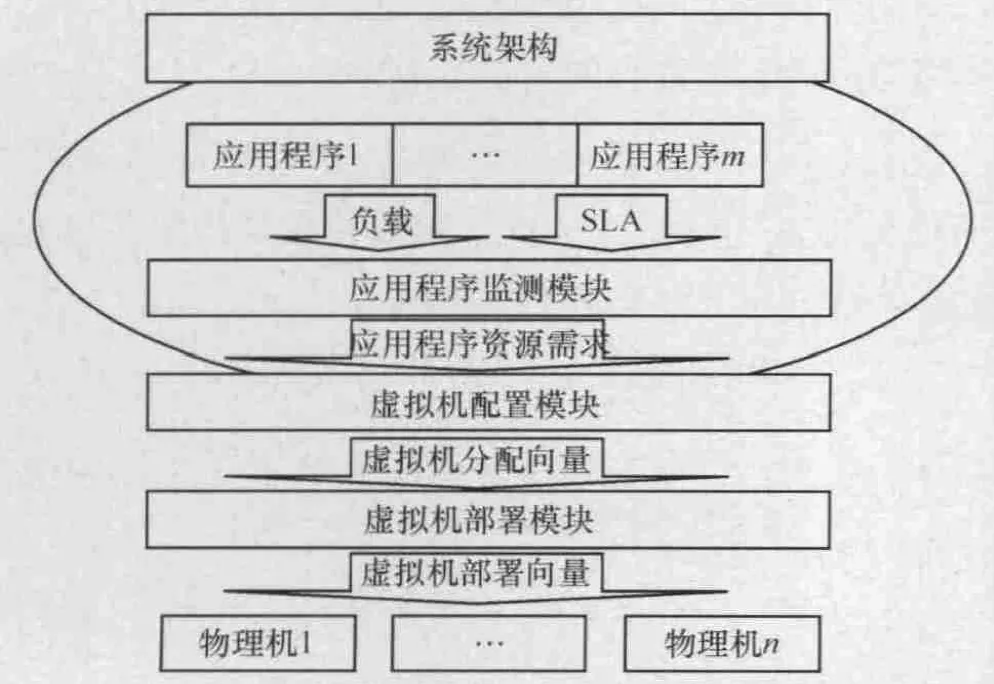
图2 基于CSP的能耗优化的云资源调度框架

从图2可以看出，提出的基于CSP的能耗优化的云资源调度框架由应用程序检测、虚拟机配置和虚拟机部署3个模块组成。本文将在3.2节～3.4节分别对各模块进行详细描述。在详细描述之前，先对部分符号进行如下说明。

3.2 应用程序监测模块

该模块首先测出各应用程序当前的负载，然后根据当前负载和 SLA目标确定分配给各应用程序的资源(CPU、memory、network)。对于应用程序ai，其分配的资源可以定义为当前负载和SLA目标的函数，即：Ri= fi(Li,Si)，其中，Li为应用程序ai的当前负载，Si为应用程序的SLA目标，Ri为分配给应用程序的资源，它是(CPU、memory、network)三元组。对于分配给应用程序ai的资源与其当前负载和SLA目标的函数关系fi，本文没有做出基于经验的或基于实验的假设，它可以由各数据中心的管理者根据相应的管理政策、经验以及大量实验数据而确定。

下面以 VAN等人[11]关于自动化虚拟资源管理研究中提到的一个基于实验数据的经验主义的性能模型(如图 3所示)为例，对应用程序监测模块进行简单说明。

图3 性能模型

水平轴表示应用程序每秒的请求量，即工作负载；垂直轴表示响应时间；图中的斜线表示特定CPU能力下响应时间与每秒请求数的关系。假设应用程序A是一个Web应用程序，其SLA目标是请求的响应时间，假设其值为100 ms，若此刻应用程序A的负载为每秒300次请求，则根据图3所示的关系可以得出分配给应用程序A的CPU能力至少为10 000 MHz。

当然，上面只是一个可能的简单示例，不同应用程序的应用程序有着不同的 SLA目标、不同类型的工作负载以及它们之间的不同函数关系。在提出的模型中，没有对这些性质做任何可能的假设，它们应该由数据中心管理员根据不同类型的应用程序，基于经验或实验数据对这些性质进行描述与设定。

3.3 虚拟机配置模块

该模块根据应用监测程序模块输出的分配给各应用程序的资源向量R=(R1,…, Rj,…, Rc)为各应用程序分配虚拟机，使总的分配代价最小。换句话说，该模块的目的是给出使目标函数(1)最小化的各应用程序的虚拟机分配向量为

其中，m为应用程序的数目，cost为虚拟机的操作开销向量，每一项对应于每一类虚拟机的分配开销，Ni为分配给应用程序i的虚拟机向量，并且Ni=（ni1,…,nij,…, nic），而nij为分配给应用程序 i的第j类虚拟机的数量，cost·Ni则表示分配虚拟机向量Ni给应用程序i的开销。

根据本文的假设，数据中心中每类虚拟机的数目是有限的，即拥有一个上限阈值，下面定义各类虚拟机的阈值向量为：Nmax=(n1max,…, njmax,…, ncmax），且有如下关系

分配给各应用程序资源量应满足应用程序监测模块确定的资源要求，即

同时，部署在物理机上的所有虚拟机的资源总量不能超过所有物理机的资源总量，故有如下关系

采用约束编程的方法对上述模型进行求解，即可获总花费最小的虚拟机分配向量，每一个虚拟机分配向量对应于各应用程序的虚拟机分配情况，即分配了哪类虚拟机及各类虚拟机分配的数量。

3.4 虚拟机部署模块

虚拟机部署模块将虚拟机分配模块产生的虚拟机分配向量N作为输入，然后将虚拟机分配向量N整合为表示当前所有需要运行的虚拟机集合的向量VM = (vm1,…,vmi,…,vmp)，其中，vmi= (vmiCPU, vmimemory,vminetwork)。同时数据中心提供每台物理主机的动态能耗参数。在描述物理资源约束前，先给出虚拟机放置的定义。

位向量Hi的定义为：∀pi∈P，Hi= (hi1,…,hij,…, hip)，hij=1当且仅当虚拟机vmj部署在物理机pi上。

对于每台物理机和其上部署的虚拟机有如下的约束关系

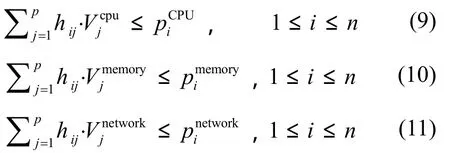
根据文献[28]可知，物理服务器的能耗为空闲时产生的能耗和其上运行的应用所产生的能耗之和为E = Edynamic+ Estatic，其中 Estatic表示物理机空闲时的能耗（即没有分配虚拟机时的能耗，物理服务器 pi上的空闲能耗用 Eistatic表示），假设物理机 pi上放置各虚拟机资源时新增能耗的向量为 Eidynamic=(ei1,… ,eik)，而 Edynamic为放置在物理服务器 pi上所有虚拟机新增能耗之和 H ⋅Edynamic。因此，可以建立异构服务器的

i i能耗最优（小）的资源调度模型为

其中，Ei为物理服务器 pi的能耗。由此可以得出关于能耗的约束条件为

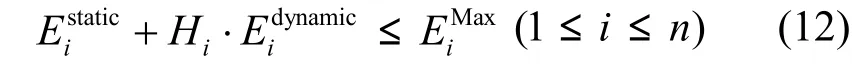
其中， EiM

ax为物理服务器 pi所能承载的最大能耗值，即物理服务器ip的实际能耗大小必须小于等于MaxiE 。

4 算法设计

4.1 虚拟机配置算法

4.1.1 算法描述

虚拟机配置算法的基本思想是为需要部署的应用搜索操作开销最小的虚拟机，并输出分配的虚拟机向量。首先将虚拟机配置问题表示成 CSP问题，采用最佳优先和剪枝的策略对其进行搜索求解。对于任一待扩展节点，如果到达该节点的路径对应的花费大于或等于最小花费值，则停止对该节点的扩展；否则，则继续扩展该节点，若该节点是最后的叶节点，则更新最小花费的值；最终返回使花费最小的虚拟机分配向量。

4.1.2 算法伪代码

算法伪代码如下所示。

1) Input ∶ pmList,vmList, AE,wights

2) Output ∶ allocation vector of VM

3) minCost MAX

4) queue new priority_queue()

5) root new node()

6) queue.push(root)

7) while queue is not empty do

8) parent queue.top()

9) queue.pop()

10) cost estimateCost(root);

11) if cost ＞ = minCost then continue

12) app the next application in AE

13) if app == NULL then

14) minCost cost

15) else

16) foreach vm in vmList do

17) if constraints are satisfied then

18) allocate vm to app

19) child new node(root,app)

20) queue.push(child)

21) return allocation vector of VM that minimizes allocation cost

4.1.3 算法性能分析

在虚拟机配置模块中，假定应用程序数为m，预定义的虚拟机种类数为 c，对于每一类虚拟机都有一个允许被分配的最大数目，设d是所有这些最大数目中的最大值，则对于每个应用程序，可以分配的虚拟机数量最多为cd；根据式(2)～式(8)可知，一共有3m+c+1个约束条件；根据RIVIN等人关于CSP代数求解的研究[27]，对于一个有n个变量，每个变量取值数为m以及M个约束条件的CSP问题，其算法复杂度为O(nm·2M-n)，故虚拟机配置模块的算法复杂度为O (cdm·22mfc)。

4.2 虚拟机部署算法

4.2.1 算法描述

虚拟机部署算法的基本思想是为需要创建的虚拟机搜索能耗最小的物理主机分配向量，并输出分配的物理主机向量。将虚拟机部署模块也表示成CSP问题，采用最佳优先和剪枝的策略来对其进行求解。在搜索前，首先需要对虚拟机分配向量进行重整，使之成为包含所有待分配虚拟机的简单向量。在搜索中，对于任一待扩展节点，如果到达该节点的路径对应的能耗大于或等于最小能耗值，则停止对该节点的扩展；否则，则继续扩展该节点，若该节点是最后的叶节点，则更新最小能耗的值，最终返回使能耗最小的虚拟机放置向量。

4.2.2 算法伪代码

算法伪代码如下所示。

1) Input ∶ pmList, allocation vector N, dyList

2) Output ∶ placement vector of VM

3) VM collapses(N) //collapses N into a single vector VM = (vm1,…, vmp)

4) minPower upperbound(pmList,VM,dyList)

5) queue new priority_queue()

6) root new node()

7) queue.push(root)

8) while queue is not empty do

9) parent queue.top()

10) queue.pop()

11) power = estimatePower(root);

12) if power ＞ = minPower then continue

13) vm the next virtual machine in VM

14) if vm == NULL then

15) minPower power

16) else

17) foreach pm in pmList do

18) if constraints are satisfied then

19) allocate vm to pm 20) child new node(root, pm)21) queue.push(child)

22) return placement vector of VM that minimizes power consumption

4.2.3 算法性能分析

在虚拟机部署模块中，假定要被分配的虚拟机数为 p，物理机数为 n，则对于每一个物理机，最多只能部署p个要被分配的虚拟机；根据式(9)～式(12)可知，一共有4n个约束条件；根据RIVIN等人关于CSP代数求解的研究[27]，对于一个有n个变量，每个变量取值数为m以及M个约束条件的CSP问题，其算法复杂度为O(nm·2M-n)，故虚拟机部署模块的算法复杂度为O(pn·8n)。

5 实验与结果

5.1 算法模拟实现

为了验证提出的模型和算法，本文进行了模拟实验。在提出的模型中，虚拟机配置和部署问题均被定义为约束满足问题，然后使用基于JAVA的约束编程CHOCO对它们进行建模和求解，模拟实验按如下步骤进行。

1) 在应用程序监测模块，根据应用程序当前负载和SLA目标，获得各应用程序所需的资源量，同时设置或调整各应用程序的权重。

2) 根据应用程序监测模块的输出，虚拟机配置模块反复探求所有可能的虚拟机分配方案，找出平均花费最小的分配方案。

3) 根据虚拟机配置模块的输出，虚拟机部署模块以最小化数据中心能耗为目标，将需要被分配的虚拟机部署到物理节点上。

4) 增加应用程序的数量，预定义虚拟机的种类数量以及数据中心物理机的数量，重复步骤 1)～3)的过程。

下面分别列出虚拟机配置模块和虚拟机部署模块中模型中约束的实现方法。

(a)虚拟机配置模块

约束式(2)：addConstraint(Choco.leq(Choco.sum(dualpos[i]),VMMAX[i]));

约束式(3)～式(5)：addConstraint(Choco.geq(ACPU[i],APCPU[i]));addConstraint(Choco.geq(AMEM[i],APRAM[i]));addConstraint(Choco.geq(ABW[i],APBW[i]));

约束式(6)～式(8)：addConstraint(Choco.leq(Choco.sum(ACPU),CPUMAX));addConstraint(Choco.leq(Choco.sum(AMEM),RAMMAX));addConstraint(Choco.leq(Choco.sum(ABW),BWMAX));

(b) 虚拟机部署模块

约束式(9)～式(12)：addConstraint(Choco.leq(Choco.scalar(dualpos[i],VMCPU),PMCPU[i]));addConstraint(Choco.leq(Choco.scalar(dualpos[i],VMRAM),PMRAM[i]));addConstraint(Choco.leq(Choco.scalar(dualpos[i],VMBW),PMBW[i]));addConstraint(Choco.leq(Choco.plus(DYNAMICPower[i],PMSTAPOWER[i]), PMax[i]));

5.2 实验环境和实验数据

为了验证提出的能耗优化资源分配算法（DY，dynamicpower），在物理主机不同异构性的情况下进行了一些模拟实验，对提出的算法DY与已有的算法 MinPM[4]、FFD[22]、BFD[22]在性能和能耗两方面进行了比较。本文在16组不同资源数量的环境下进行算法模拟实验，每组模拟实验中的虚拟机数和物理机的数量为：10×实验组号，即 16组实验中虚拟机数和物理机的数量分别为：10，20，30，…，160。而且，分别在物理主机的能耗异构性不同的2种情况下进行实验。其中能耗异构性的大小是根据物理机上的能耗参数决定的，如果一组中各物理主机能耗参数相差越大，则该组物理机的异构性越大。实验中物理主机的能耗参数数据的生成规则如下。

1) 异构性小的物理主机能耗参数设置

空闲能耗：100～300之间。将其分为100～150,150～200, 200～250, 250～300 4 组，依据物理主机的资源大小，选择其中一个组，随机生成数据，选择原则一般依照：资源大的，能耗较小。以下选择的原则相同。

最大能耗：1 000～2 000之间。将其分为1 000～1 250, 1 250～1 500, 1 500～1 750, 1 750～2 000 4 组，同样依据物理机主机的资源大小，选择其中一组，随机生成数据。

2) 异构性大的物理主机能耗参数设置

空闲能耗：100～500之间。将其分为100～200,200～300, 300～400, 400～500 4 组，依据物理主机的资源大小，选择其中一组，随机生成数据。

最大能耗：800～3 500之间。 将其分为800～1 500,1 500～2 200, 2 200～2 900, 2 900～3 600 4组，依据物理主机的资源大小，选择其中一组，随机生成数据。

另外，实验中物理主机和虚拟机的资源大小参数的设置如下。

1) 物理主机的资源参数设置PMCPU：2 ～32 GHz //CPU；PMRAM：2～32 GB//内存；PMBW：100～500 M//带宽。

2) 物理主机的资源参数设置VMCPU：256 MHz～10 GHz//CPU；VMRAM：256 MB～10 GB//内存；VMBW：30 ～120 M//带宽。

5.3 实验结果

图4(a)～图4(d)分别是物理主机能耗异构小与异构大 2种实验环境下 DynamicPower(DY)、MinPM、FFD、BFD 4个算法资源分配的能耗情况。其中，纵坐标为能耗（单位为Wh），横坐标为实验编号。从图4中可以看出，本文提出的能耗优化资源分配算法DY和MinPM算法，随着物理主机数和虚拟机数的增加，能耗的节省要优于FFD和BFD算法，这主要是因为FFD和BFD只是寻求一个合理的资源分配解，而不是寻求能耗最优的资源分配解。就DY和MinPM 2种算法而言，DY要优于MinPM，因为DY算法考虑虚拟机动态能耗求得综合能耗最小的资源分配方式，而 MinPM 仅仅是求物理主机数的最小值，所以DY算法得到的能耗始终是小于MinPM的能耗。将图4(a)～图4(d)对比可以看出，当物理机的异构性越大时DY算法的能耗减少得更明显。

为了更好地分析物理主机的能耗异构性大小对资源分配结果的影响，下面给出2种异构环境下的能耗节能的比例情况，见图 5(a)和图 5(b)。其中，图 5(a)和图 5(b)分别表示图4中各组实验中4种算法的能耗与最大能耗相比所节省的能耗百分比。从图中可以看出，异构性大的环境下DY算法节省的能耗均在50%左右，而异构性小的环境下DY算法节省的能耗在40%左右，即异构性小环境下节能百分比明显大于异构性大环境下节能百分比。

(a) 物理主机异构小环境的能耗1

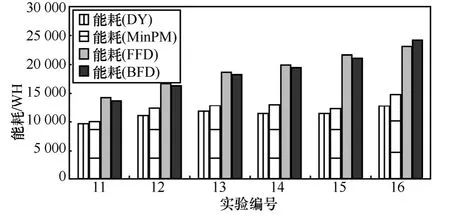
(b) 物理主机异构小环境的能耗2

(c) 物理主机异构大环境的能耗1

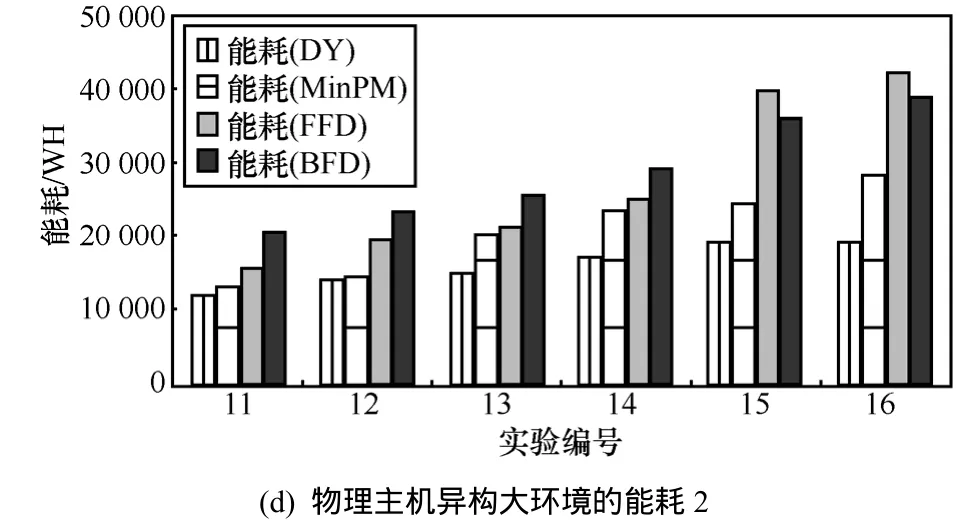
图4 能耗比较

除了能耗优化的考虑外，还需要考虑算法的运行效率的问题。图6是图4中各算法在各组实验中所对应的运行时间。

图5 节能百分比

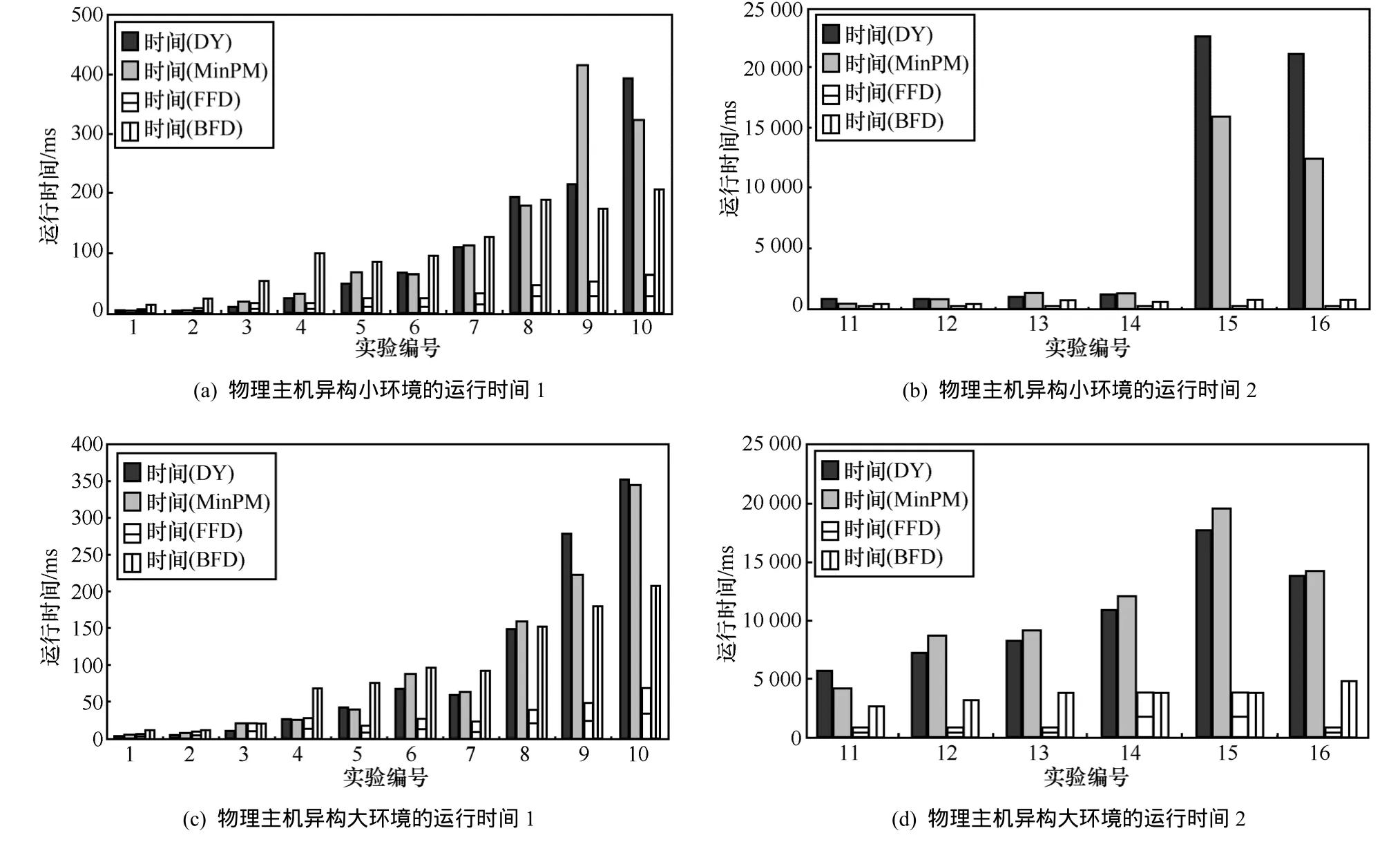
图6 算法运行时间比较

图6 (a)和图6(b)分别表示图4中各组实验的运行时间，纵坐标为运行时间，单位为毫秒(ms)。从上图中均可以看出，随着物理主机和虚拟机数的增加，DY和MinPM算法在运行时间上有比较明显的增加，而FFD和BFD 2种算法相比之下在运行效率上则具有很明显的优势，尤其是在物理机和虚拟机数量增加的情况下，这种优势越加明显。DY的运行效率则略优于 MinPM 算法，在物理主机异构性较大的情况，则DY的运行效率的优势更大，这主要是因为DY算法约束条件相比MinPM算法更多，搜索空间更小，所以求解更快。

6 结束语

本文主要研究在物理服务器异构情况下的能耗优化的资源调度问题。由于物理主机资源和能耗的异构，不同种类的虚拟机分配到同一物理主机上产生的动态能耗也不同。此时，能耗优化的问题并不是最小物理主机数。针对该问题，提出了一个基于CSP的能耗最优的资源调度模型，该模型支持异构应用程序和工作负载，并且同时支持增加资源到单节点的垂直伸缩方式和增加节点数的水平伸缩方式。在该模型中，将虚拟机的资源配置从虚拟机的动态部署中分离出来。虚拟机的资源配置模块旨在根据用户 SLA要求确定代价最小化的资源配置方案，虚拟机的动态部署旨在最优化数据中心的能源消耗。本文将这2个问题建模为约束满足问题，采用约束规划的方法求解该优化问题。模拟实验的结果验证了本文提出的能耗最优模型与算法的有效性。本文提出的模型和算法可以应用到云数据中心，不仅可以减少云数据中心的能耗和经营成外，而且这项工作还具有重要的社会意义，因为它可以减少现代IT基础设施CO2的释放量和能源的消耗量。

[1] BUYYA R, YEO C S, VENUGOPAL S. Market oriented cloud computing∶ vision, hype, and reality for delivering IT services as computing utilities[A]. HPCC’08[C]. Dalian, China, 2008. 5-13.

[2] BELOGLAZOY A, BUYYA R, LEE C Y, et al. A taxonomy and survey of energy-efficient data centers and cloud computing systems[J]. Advances in Computers, 2011,(82)∶47-111.

[3] GARG S K, YEO C S, ANANDSIVAM A, et al. Environmentconscious scheduling of HPC applications on distributed cloud-oriented data centers[J]. Journal of Parallel and Distributed Computing, 2011,71(6)∶ 732-749.

[4] BICHLER M, SETZER T, SPEITKAMP B. Capacity planning for virtualized servers[A]. WITS’06[C]. Milwaukee, Wisconsin, USA, 2006.1-6

[5] KHANNA G, BEATY K, KAR G, et al. Application performance management in virtualized server environments[A]. NOMS 2006[C].Vancouver, BC, 2006. 373-381.

[6] VERMA A, AHUJA P, NEOGI A. pMapper∶ power and migration cost aware application placement in virtualized systems[A]. Middleware'08 [C]. New York, NY, USA∶ Springer-Verlag, 2008. 243-264.

[7] HERMENIER F, LORCA X, MENAUD J M, et al. Entropy∶ a consolidation manager for cluster[A]. VEE’09[C]. New York, NY,USA∶ ACM, 2009. 41-50.

[8] RIETZ J, MACEDO R, ALVES C, et al. Efficient lower bounding procedures with application in the allocation of virtual machines to data centers[J]. WSEAS Transactions on Information Science And Applications, 2011, 4(8)∶157-170.

[9] BATU R R T, WHITE P. Fast approximate PCPs for multidimensional bin-packing problem[J]. Lecture Notes in Computer Science, 1999,1671∶245-256.

[10] TIAGO C F, MARCO A S N, RODRIGO N C, et al. Server consolidation with migration control for virtualized data centers[J].Future Generation Comp Syst, 2011, 27(8)∶ 1027-1034.

[11] VAN H N, TRAN F D, MENAUD J M. SLA-aware virtual resource management for cloud infrastructures[A]. CIT’09[C]. Washington DC,USA, 2009.357-362.

[12] VON LAZEWSKI G, WANG L, YOUNGE A J, et al. Power-aware scheduling of virtual machines in DVFS-enabled clusters[A].CLUSTER’09[C]. New Orleans, LA, USA, 2009.1-10.

[13] LIU L, WANG H, LIU X, et al. Greencloud∶ a new architecture for green data center[A]. ICAC-INDST '09[C]. New York, NY, USA,ACM, 2009.29-38.

[14] HARALICK R, ELLIOTT G. Increasing tree search efficiency for constraint satisfaction problems[J]. Artificial Intelligence, 1980, 14(3)∶263-313.

[15] JUSSIEN N, ROCHART G , LORCA X. The CHOCO constraint programming solver[A]. OSSICP’08[C]. Paris, France, 2008.

[16] SRIKANTAIAH S, KANSAL A, ZHAO F. Energy aware consolidation for cloud computing[A]. HotPower'08[C]. Berkeley, CA,USA, 2009. 1-15.

[17] BERL A, GELENBE E, GIROLAMO M, et al. Energy-efficient cloud computing[J]. The Computer Journal, 2010, 53(7)∶ 1045-1051.

[18] BELOGLAZOV A, BUYYA R. Energy efficient resource management in virtualized cloud data centers[A]. CCGRID ‘10[C]. Washington DC,USA, 2010. 826-831.

[19] RODERO I, JARAMILLO J, QUIROZ A. Energy-efficient application-aware online provisioning for virtualized clouds and data centers[A]. GREENCOMP’10[C]. Washington DC, USA, 2010.[20] 3A1B-4D5E.LSALAM H S, MALY K, KAMINSKY D. Analysis of energy efficiency in clouds[A]. Computationworld '09[C]. Washington DC,USA, 2009.416-422.

[21] YOUNGE A J, LASZEWSKI G , WANG L. Efficient resource management for Cloud computing environments[A]. GREENCOMP’10[C].Washington DC, USA, 2010. 357-364.

[22] CHANG F, REN J, VISWANATHAN R. Optimal resource allocation in clouds[A]. CLOUD’10[C]. Washington DC, USA, 2010. 418-425.

[23] LEE Y C, ZOMAYA A Y. Energy efficient utilization of resources in cloud computing systems[J]. The Journal of Supercomputing, 2012,60(2)∶ 268-280.

[24] KARMARKAR N, KARP R M. An efficient approximation scheme for the one-dimensional bin-packing problem[A]. FOCS’82[C].Washington DC, USA, 1982. 312-320.

[25] BELOGLAZOV A, ABAWAJY J H, BUYYA R. Energy-aware resource allocation heuristics for efficient management of data centers for cloud computing[J]. Future Generation Comp Syst, 2012, 28(5)∶755-768.

[26] KUMAR V. Algorithms for constraint satisfaction problems∶ a survey[J]. AI Magazine, 1992, 13(1)∶ 32-44.

[27] RIVIN I, ZABIH R. An algebraic approach to constraint satisfaction problem[A]. IJCAI'89[C]. San Francisco, CA, USA, 1989. 284-289.