液氮容器蒸发流量对压力阶跃变化的动态响应

刘惠民 邵雪锋 冯慧华

(上海船用柴油机研究所 上海 201203)

液氮容器蒸发流量对压力阶跃变化的动态响应

刘惠民 邵雪锋 冯慧华

(上海船用柴油机研究所 上海 201203)

对低温液氮容器在受到压力变化时的温度响应进行了动态分析，针对压力阶跃变化的特殊情况进行了温度响应的数值计算。结果表明，通常的蒸发率测试过程中，容器内液体是需要很长时间才能达到平衡状态的，但压力变化对蒸发流量的影响将随着时间衰减很快。提出了在压力阶跃变化情况下的蒸发流量的修正方法，并得到了试验验证。

蒸发流量 低温容器 压力阶跃变化 温度响应

1 引言

蒸发率是评定低温容器绝热性能的最重要的技术参数。理论研究表明，当夹层真空度优于10-3Pa后，其表观导热系数曲线趋于水平［1-2］，即容器漏热量不再受环境温度变化的影响。但是对于高真空多层绝热容器的实际测试表明，蒸发流量仍会出现周期性的明显波动，对此现象，文献［3-5］进行了试验测量和定性分析，认为是环境压力的波动造成了蒸发流量的瞬态变化。文献［6-7］从理论和试验验证角度揭示了蒸发流量波动同时受环境压力和环境压力变化率的双重影响，但没有进一步提出对环境压力的有效可行的修正方法。

本文考察了低温容器内液体的传热机理，得到了在压力阶跃变化情况下的液体温度响应关系，分析了容器在不同阶跃压力对蒸发流量的影响程度，并提出了修正压力变化影响的方法，并通过3.5 m3高真空多层绝热液氮低温容器的蒸发流量试验验证了修正方法的可行性。

2 蒸发量计算模型的建立

2.1 模型及假设

计算模型如图1所示。定义在一个任意时刻t时容器内所有液体所含的空间为控制容积，系统边界由气、液相分界面以及液体与容器内壁面的边界组成。对系统做出如下假设:(1)由于压力变化速率很小，气液界面可视为处于热力平衡状态，界面温度就等于系统压力下的液体的饱和温度;(2)压力为阶跃变化;(3)容器四周和底部绝热，只考虑由压力变化产生的界面蒸发，故系统可视为一维导热;(4)介质的导热系数和扩散系数视为常数。

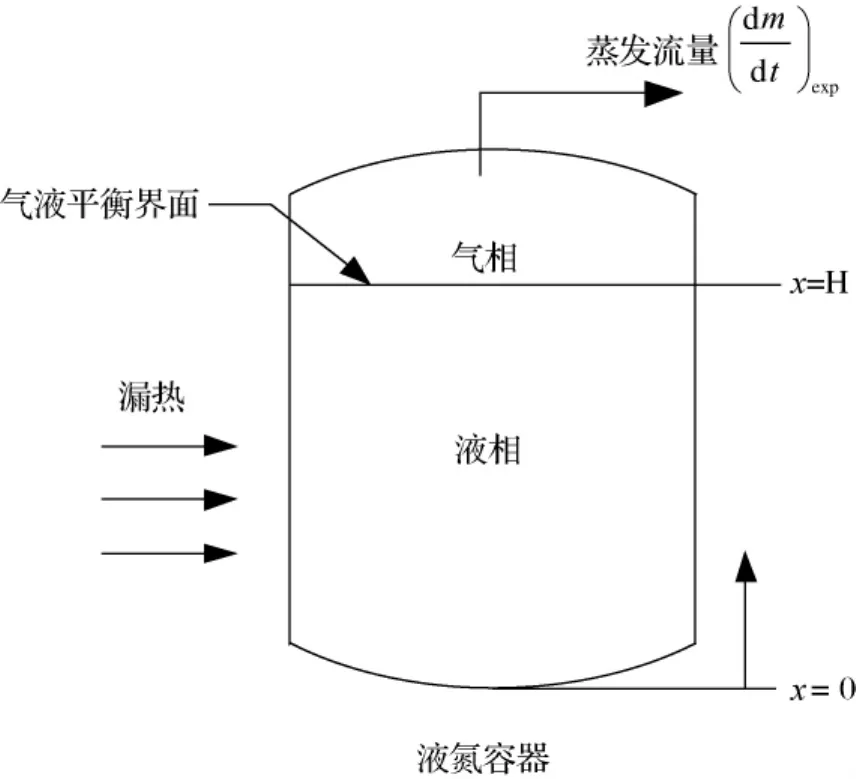
图1 液氮低温容器蒸发数学模型Fig.1 Schematic diagram of LN2boil-off model

2.2 数学方程

由假设条件，系统为一维扩散方程:

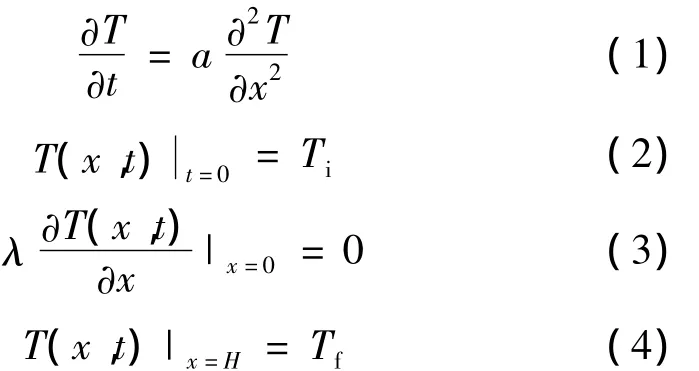
式中:a为液氮的热扩散率，m2/s;λ为液氮的导热系数，W/(m·K);Ti为系统的初始温度，K;Tf为气液界面的最终温度，等于对应压力下的液体饱和温度，K。

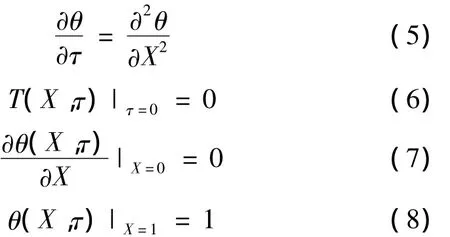
由式(5)—式(8)可以得到任意时刻容器内液氮的无因次温度分布。

气液界面梯度为:

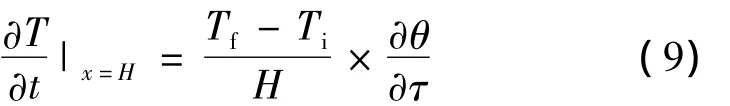
由此可以得到气液界面由于压力变化而产生的蒸发流量:

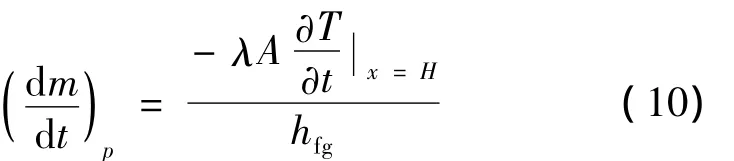
2.3 分析和讨论

图2给出了无因次温度随无因次时间和无因此位置的变化关系，图3给出了气液界面无因次温度梯度随时间的变化关系。

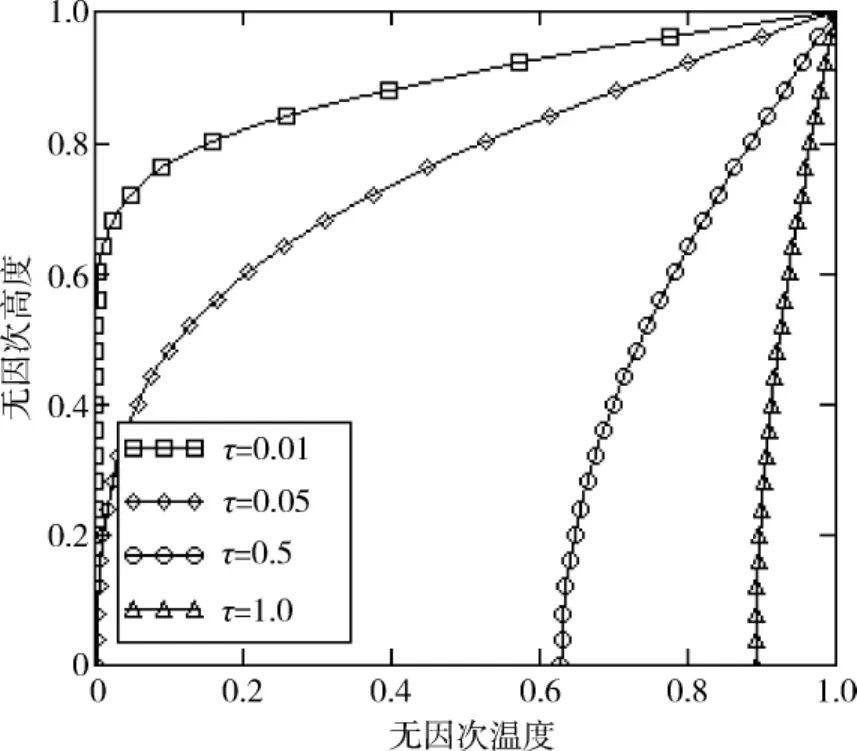
图2 无因次温度随无因次时间和无因次位置的关系Fig.2 Calculated dependence of dimensionless temperature with different dimensionless time and dimensionless height

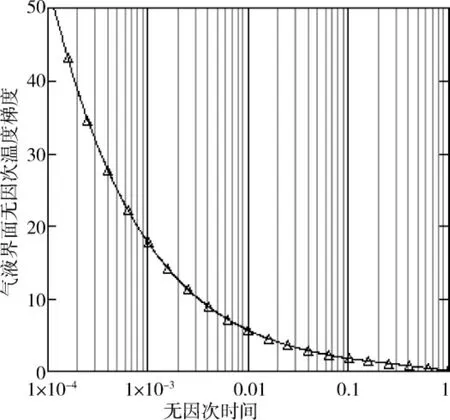
图3 气液界面处无因次温度梯度随时间的变化Fig.3 Calculated dependence of dimensionless temperature gradient at vapor/liquid interface with dimensionless time

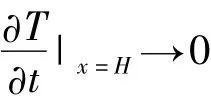
可见，在没有外部漏热或内部热源引起液体扰动的假想情况下，整个液体达到平衡状态的时间将大于3 160 h，远大于一般蒸发率试验中测量的间隔时间。这说明，如果出现阶跃压力变化，大多数试验中液体基本不会达到整体平衡。

压力增加时的结果由图4给出，蒸发流量为负值，即界面处发生液化。反之，压力减小时，蒸发流量为正值，即界面处发生汽化。由图可知，界面的蒸发流量及其变化速率在最初的时间内衰减很快，间隔1 h后，蒸发流量及其变化速率趋于平稳，相对初始状态已经小很多，可以认为界面达到了准平衡，此时测量得到的数值较为稳定。

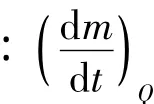
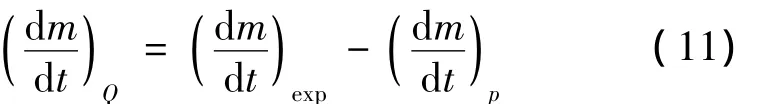
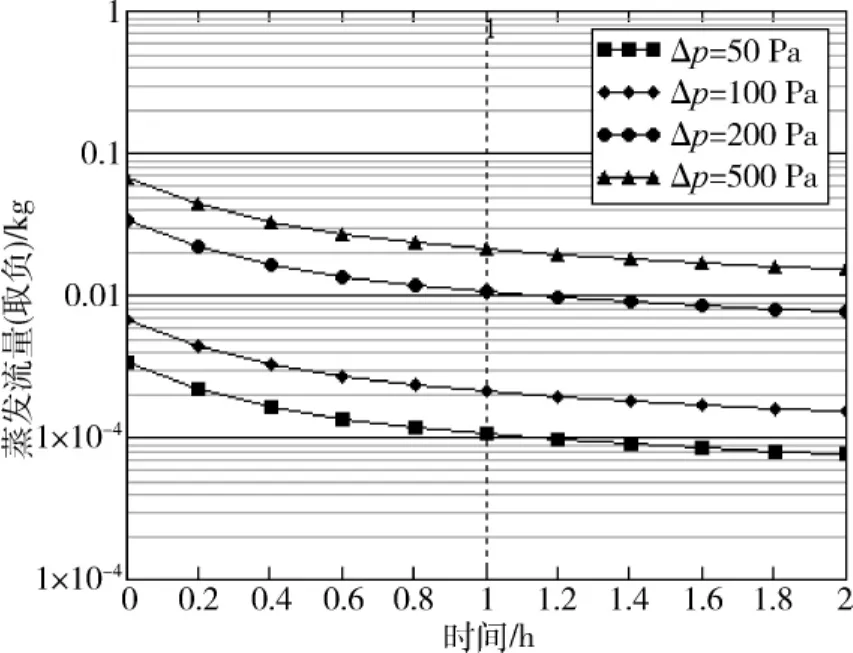
图4 蒸发流量随时间和阶跃压力的计算值Fig.4 Calculated variation of boil-off rate with time and step change

3 试验

3.1 试验系统及流程

对3.5 m3高真空多层绝热低温容器进行蒸发率测试，试验系统如图5所示。质量流量计采用热式气体质量流量计，量程为0.4—9.4 kg/h，精度为±1%FS;压力传感器采用高稳定性绝对压力传感器，量程10 kPa—70 MPa，精度±0.04%FS。试验流程按照国家标准《真空绝热深冷设备性能试验方法—第5部分:静态蒸发率测量》(GB/T18443.5-2010)进行。

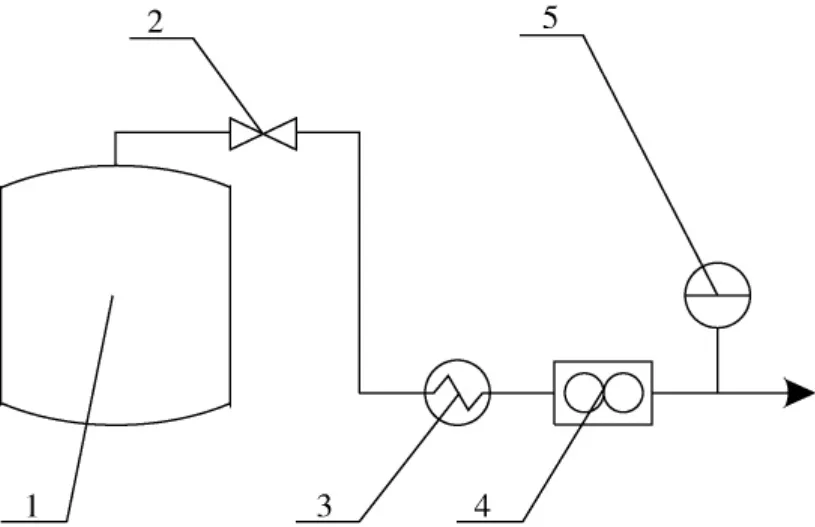
图5 蒸发率试验系统图1.液氮容器;2.泄放阀;3.加热器;4.质量流量计;5.绝对压力传感器Fig.5 Configuration of devices during LN2 boil-off measurement

3.2 试验结果分析

图6为蒸发率试验时得到的实测蒸发流量和环境压力曲线。由图可见，实测蒸发流量呈现不断波动的现象，波动趋势与大气压变化趋势反向，有一定的滞后。最大流量与最小流量相差可达30%以上。表明蒸发流量受大气压变化的影响很大，因此有必要对蒸发流量的测量数据进行修正，以消除大气压力波动对蒸发流量的影响。

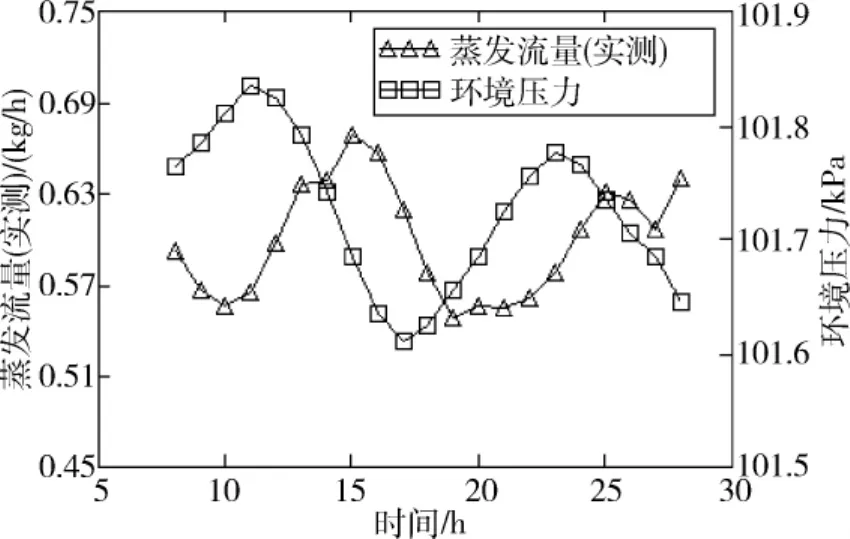
图6 蒸发流量与环境压力的变化关系Fig.6 Variation of mass flow with atmospheric pressure

图7给出了实测蒸发流量和修正后蒸发流量的对比。从图中可以看出，修正后蒸发流量波动明显较修正前稳定。修正后的蒸发流量是由于容器漏热而产生，这也从侧面说明了对于高真空多层绝热容器，环境温度的变化不是蒸发流量波动的主要影响因素，容器漏热量几乎不受外界环境温度变化的影响。修正后的蒸发流量真实反映了容器的绝热性能。

4 结论

建立了低温液氮容器受压力变化时的动态温度响应，分析讨论了压力阶跃变化这一特殊情况对蒸发流量的影响，并对蒸发率试验的测量结果进行了压力变化的修正，得出以下结论:

(1)对于气液界面的压力变化，容器内液氮由于较低的扩散特性而需要经历很长时间才能达到整体温度平衡，所需的时间远大于一般试验中采用的时间测量间隔。由于压力变化而引起的蒸发流量和蒸发流量的变化率在最初时间衰减很快，而间隔1 h后测量得到的数据较为稳定。

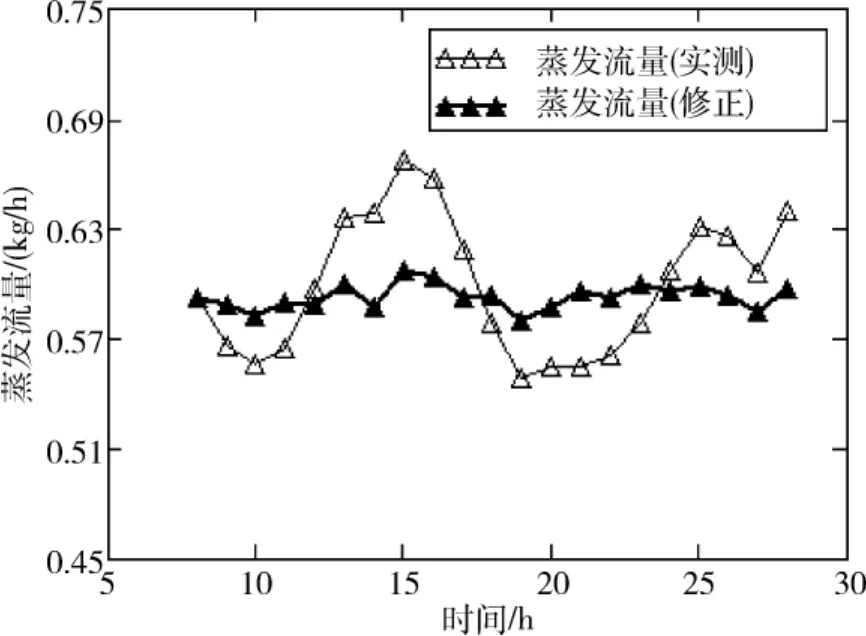
图7 实测蒸发流量和和修正结果对比Fig.7 Comparison of experimental andcorrected mass flow

(2)在蒸发率试验中，应对实际测量得到的蒸发流量进行修正，消除由于压力变化产生的影响，修正后的蒸发流量才能真实反映容器的绝热性能。

1 符锡理.高真空多层绝热理论研究和传热计算［J］.低温工程，1989(2):1-11.

2 符锡理.低温容器蒸发率的测定和评定［J］.低温与特气，1988(3):56-60.

3 刘根仓，汪荣顺.环境温度对高真空多层绝热性能影响的试验研究［J］. 低温工程，2010(3):22-25.

4 陈喜海，汪荣顺.低温容器蒸发率试验及蒸发量波动分析［J］.低温工程，2010(2):42-45.

5 Pavel Hanzelka，Jaroslav Horky.Problems of measurement of the helium boil off rate of tomographic magnets［J］.Cryogenics，1999(39):647-649.

6 刘惠民，冯慧华.环境压力对低温容器蒸发流量的理论分析和试验验证［J］. 低温工程，2012(2):60-64.

7 Hanzelka P，Musilova V.Influence of changes in atmospheric pressure on evaporation rates of low-loss helium cryostats［J］.Cryogenics，1995(35):215-218.

Influence of boil-off mass flow on step change in atmospheric pressure of liquid nitrogen tank

Liu Huimin Shao Xuefeng Feng Huihua

(Shanghai Marine Diesel Engine Research Institute，Shanghai 201203，China)

The dynamic analysis of temperature influence with pressure variations for a liquid nitrogen tank was described.The numerical solution was put forward for the special case when the tank was subjected to a step change in atmospheric pressure.The results indicates that the time requirement of system to reach equilibrium was exceedingly long compared to the duration of most of the experiments.However，the influence of the pressure variation decreases sharply with time initially.A correction was provided to account for the effect of pressure variation and verified by the boil-off experiment.

boil-off mass flow;cryogenic vessel;step change in atmospheric pressure;temperature response

TB611

A

1000-6516(2013)04-0065-04

2013-05-20;

2013-07-24

刘惠民，男，32岁，硕士、工程师。