利用数值法改进大学物理课中的演示实验
2013-09-17雷前召
雷前召
(渭南师范学院物理与电气工程学院,陕西渭南714000)
物理学是一门实验科学[1],其教学的各部分内容均程度不同地和实验相关.由于教学资源的限制[2],学生亲自操作的分组实验和理论教学很难做到同步进行;而教师的课堂演示实验往往因为实验设备不完善、仪器不精密导致实验现象不明显;或者因为实验繁琐,耽误时间影响教学进度.而采用数值计算方法[3]对实验进行模拟则可以克服这些缺陷,随着多媒体教学的普及,利用数值法模拟演示实验不仅是必要的,更是方便易行的.
1 模拟物理过程,有利于观察中间细节
大学物理中的机械波概念,其中的横波能够通过实验比较直观地将其波形展现出来,但纵波却很难在实验中展示波形.可以通过模拟弹簧动画来演示纵波的物理过程[4].
弹簧动画的模拟就是一个算法设计[5],利用椭圆方程x=x0+a cosθ,y=y0+b sinθ画椭圆代表弹簧模型,选取弹簧上32个点,标记其初始中心位置为参考位置点,将弹簧上选定点的各时刻的实时位置(振动偏移位置)和初始中心位置对比确定弹簧各中心点的位移.
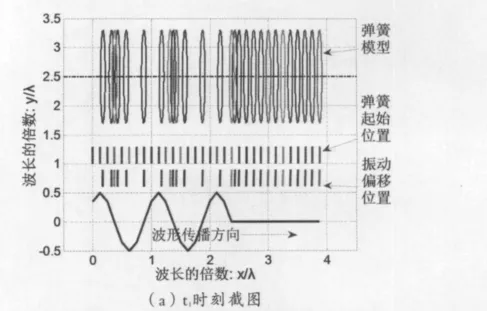
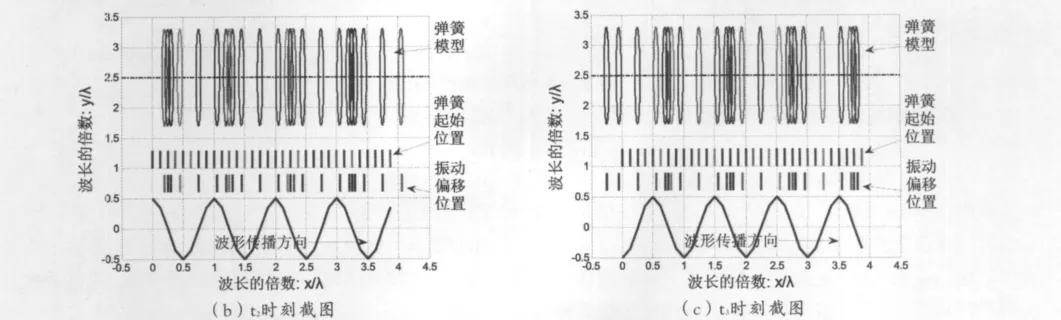
图1 弹簧模型、起始位置、偏移位置及波形传播动画截图
设椭圆方程中的a、b分别为0.04和0.8个波长,弹簧各点在其参考位置附近做简谐振动,模拟结果如图1所示.图1中从上往下依次为弹簧模型(显示各部分在该时刻的位置)、弹簧各部分中心点的起始位置及实时的各部分中心点的位置,后两者位置之差为其振动偏移量;图形底部为正弦波形,其纵向坐标即弹簧各点振动偏移量(此处按同比例放大3.5倍做出).
图1中各图正弦波的纵坐标为正的各个点,代表弹簧的位置在平衡位置右侧,偏离右侧越远,其纵坐标值越大;当纵坐标为负,实际位置在其平衡位置左侧,偏离左侧越远,其纵坐标值越小.在弹簧稀疏之处,弹簧相互间是拉力;而在弹簧处于紧密时,相互间是推力,弹簧的这种推拉之力正是弹簧振子的回复力,使得各点始终在自己的平衡位置附近振动,而振动的波形向前传播形成纵波,纵波的波动图像符合正弦规律.经过数值模拟,纵波的物理图像[6]变得清晰起来.
2 对比参数变化,参数意义明显
我们知道光栅衍射是单缝衍射和多缝干涉的综合效果.光栅衍射的光强公式为[7]

其中:u=πa sinθ/λ,v=πd sinθ/λ,其中的第一个分式是单缝衍射因子,第二个分式为缝间干涉因子[8].可以看出光栅衍射光强除了和电磁波波长λ有关外,还和缝宽a、缝间距d和光栅缝数N三个参数有着密切的关系.这种复杂关系使得各个参数的作用变得不易理解,如果借助一定形式的演示实验,课堂讲授就容易得多.这里借助数值计算得到电子版的模拟演示实验.
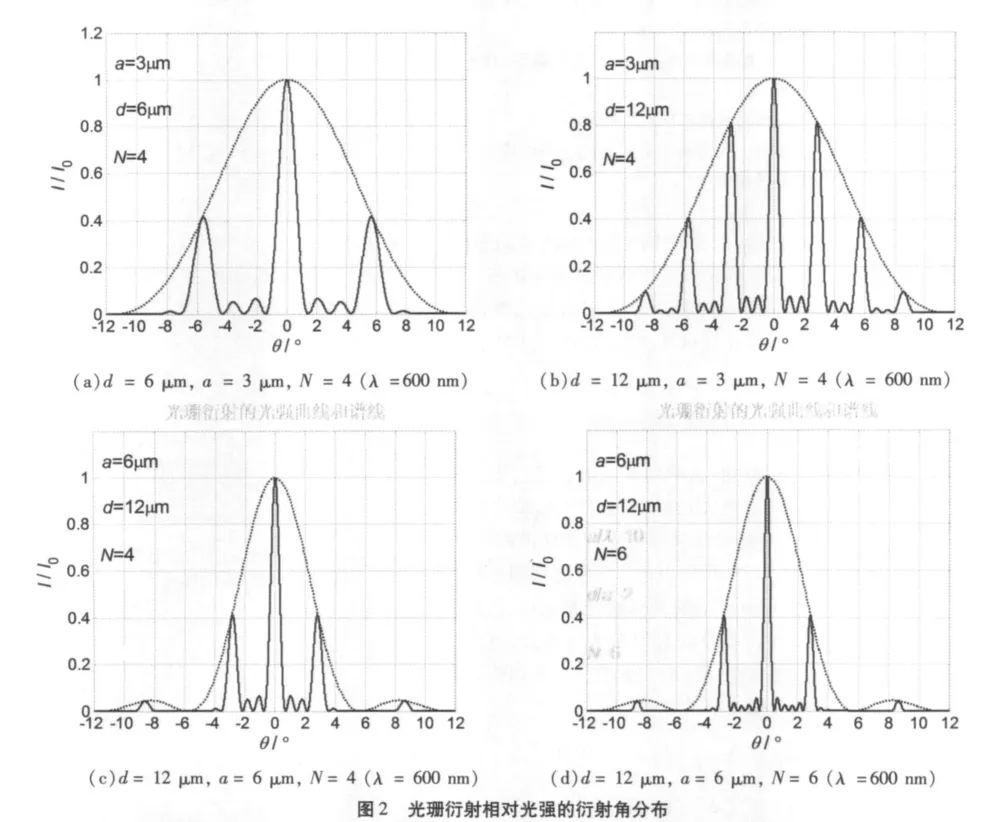
参数选取:设电磁波波长λ=600 nm不变,分别选择另外几个参数进行对比:(1)光栅常数d=6μm,缝宽 a=3μm,设光栅缝数N=4;(2)光栅常数d=12μm,缝宽a=3μm,设光栅缝数N=4;(3)光栅常数d=18μm,缝宽a=6μm,设光栅缝数N=4;(4)光栅常数d=18μm,缝宽a=6μm,设光栅缝数N=6.模拟结果如图2(a)、(b)、(c)和(d)所示.
模拟结果分析:
相同参数下,改变光栅常数d,中央明纹内主极大的条数就会改变.图2(a)和图2(b)分别对应d/a为2和4的情况,图2(a)中央明纹内有2个主极大,其中第2个主极大处于缺极位置;图2(b)中央明纹内有4个主极大,第4个主极大处于缺极位置.
保持 d/a和缝数N的值不变,改变缝宽a,中间明纹的宽度就会改变.图2(c)和图2(d)对应的a为6 μm;图2(a)、(b)对应的a为3μm,可以看出当a增大1倍,中间明纹的宽度会缩小1倍,反之亦然.
保持缝宽a和光栅常数d不变,改变光栅的缝数N,参见图2(c)和图2(d),单缝衍射以及各个主极大没有什么变化,但次极大的数目发生改变.当N=4时,次极大为2,当N=6时,次极大为4,次极大的数目比 N总是少2.
相信经过这样的对比,各参数的意义会变得非常清晰.
通过数值计算及模拟,同时验证了(1)式中的第一个分式是单缝衍射因子,也即强度因子,决定光栅各个主极大、极小位置;第二个分式为缝间干涉因子;同时验证了缝间干涉的明条纹形成的条件是sinθ=kλ/d(k=0,±1,±2,…),此方程即为光栅方程.
模拟结果同时可以验证缝间干涉明条纹缺级现象.单缝衍射暗条纹形成的条件是 sinθ=k'λ/a(k=±1,±2,…),如果由光栅方程决定的缝间干涉的明条纹衍射角与单缝衍射暗条纹的衍射角相等,这个明条纹就会缺失,称为缺级.所缺的级次为k=k'·d/a(k=±1,±2,…),其中 d/a是整数比.
光栅衍射的缺级现象是教学的一个难点,由于实验设备的精确度限制,即使干涉明暗条纹有时都很难清晰地观测到,缺级现象更是难以捕捉.然而通过数值模拟,缺级现象就能够准确展示,干涉明暗条纹更是准确无误地显示出来.如图3为N=3,d/a=2时红光的光栅衍射在光屏的衍射条纹模拟图,干涉条纹清晰,这里同样可以显示主极大在 ±2,±4,…处缺级.

图3 当N=3,d/a=2时数值模拟的光栅衍射的光屏分布
3 结语
本文只是挑选了物理学中的力学和光学两个典型实验利用数值计算进行了模拟分析,当然物理学各部分内容都可以类似地设计演示实验,并利用多媒体加以展示.
数值计算在大学物理课教学中不仅能有助于教师进行演示实验的模拟与仿真,而且在实现大学物理教学内容和教学手段的现代化方面能够发挥重要作用,对提高学生学习物理的积极性,提高教学效果,进而提高大学物理教学质量,培养高素质的人才都会起到非常重要的促进作用.
[1]John Losee.A Historical Introduction to the Philosophy of Science[M].Fourth edition.London:Oxford University Press,2001.
[2]许世军.大学物理实验与演示实验的一体化教学改革[J].物理通报,2001,(3):17-19.
[3]李梦霞,陈忠.《数值计算方法》直观教学研究[J].长江大学学报(自然科学版),2009,6(1):373- 374.
[4]胡盘新,钟季康.在大学物理教材中引入计算机数值解的尝试[J].物理与工程,2006,16(2):47-50.
[5]吴晓勤,熊之光,唐运梅,等.数值分析课程中算法设计的教学[J].湖南工业大学学报,2010,24(2):68-71.
[6]坚强,孙光厚,赵磊.基于数值计算与数值模拟的基础物理教学内容改革研究[J].九江学院学报(自然科学版),2010,88(1):117-120.
[7]梁绍荣,刘昌年,盛正华.普通物理学:第四分册(光学)[M].第3版.北京:高等教育出版社,2005.
[8]雷前召.迈克尔逊干涉仪测量折射率的实验研究[J].渭南师范学院学报,2011,26(10):68-74.
