接触电阻对导电纬平针织物柔性传感器的电－力学性能影响

王金凤，龙海如，李家成

（1.东华大学 纺织学院，上海 201620；2.广东瑞源科技股份有限公司，广东 普宁 515343）

目前市场上的人体健康监护设备存在价格昂贵、体积庞大、操作复杂、不能穿戴或穿戴不舒服等缺点，而由智能导电纤维及纺织技术制备的柔性传感器则可以克服以上问题.这种智能材料或者智能纺织品具有感知应力、应变、压力等功能，可以对人体的心跳、呼吸等生理参数进行实时检测.

针织物由于其独特的结构性能表现出柔软、舒适及弹性贴身等特点，因而采用智能材料制备的针织结构柔性传感器越来越受到人们的关注.针织物的拉伸状态直接关系到其变形性能，不同的力学模型[1－7]已对此进行了阐述，然而由于分析过程过于复杂，这些模型对于针织物张力与线圈间接触力的关系预测非常有限.本文通过综合运用文献[1，6]的针织物力学模型分析线圈中交叠纱线间的接触力，利用经验公式模拟预测接触电阻与接触力的关系，以便为基于针织结构柔性传感器的人体健康监护服装的研制奠定基础.

1 导电纬平针织物电阻

当一个已知电压加载于导电纬平针织物两端时，它的电阻会随施加在针织物两端的张力变化而变化.由于所用材料的高导电性，针织物的传导机制用一个纯电阻的电路网来分析.为了模拟针织物的变形，简化线圈电路的分析，作如下假设：

（1）导电纱线针织物线圈模型中纱线长度可以表述其实际长度；

（2）针织物线圈的变形是均匀的；

（3）线圈纱线除了交叠处外其他均为直线段；

（4）纱线半径相对于线圈长度的比例不超过4%（实际上是几何要求）；

（5）线圈针编弧和沉降弧长度近似相同.

导电纬平针织物的线圈结构如图1所示.一个线圈单元由2段圈柱、1段针编弧和1段沉降弧组成，从而其电阻包括4段与导电纱线自身电阻相关的纱段电阻（Rl），同时由于相互交叠的纱线间存在接触力，从而产生2个接触电阻（Rc）.由假设（5）可得，线圈针编弧和沉降弧纱段电阻近似相等，在图1中都用Rla表示，圈柱纱段电阻用Rlb表示.因此，导电纬平针织物的等效电路可以看作各纱段电阻和接触电阻组成的串并联复杂电路网.

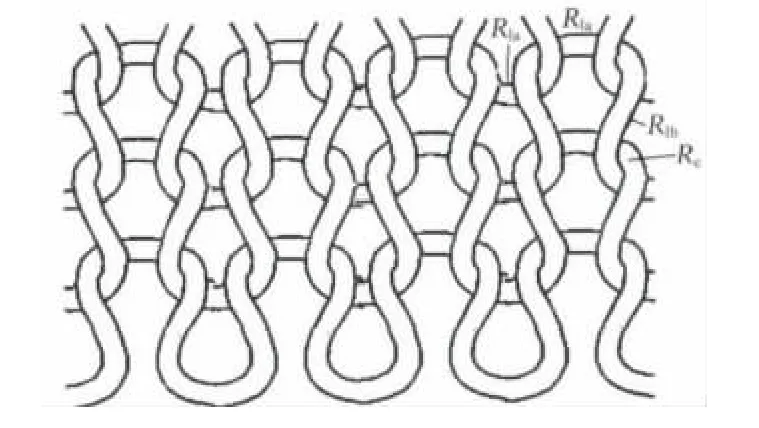
图1 导电纬平针织物结构Fig.1 A conductive weft plain knitted fabric structure

导电针织物在拉伸应变情况下，其电阻受纱线自身电阻、线圈纱段电阻转移及纱线间接触电阻3个因素的影响.金属导体电阻与它的长度成正比而与截面积成反比[8]，而随着针织物拉伸应变的增加，纱线长度增加、截面积减小，因此，纱线自身电阻随拉伸应变的增加而增加.经过笔者的理论分析和试验研究可以得知，线圈纱段电阻转移改变了导电纱线针织物的电阻，使其随横向拉伸应变的增加而线性增加.

2 接触电阻对导电纬平针织物电阻的影响

一些学者从20世纪50年代开始研究针织物的力学性能[4，9－10]，在针织物拉伸和回复过程中，线圈中相互交叠纱线在接触点处存在摩擦，交叠纱线间的接触力相应地随着针织物的伸长而变化，接触电阻也会随之变化.接触电阻与接触力的关系可从试验获得.

为了计算接触电阻与接触力的关系，假设：

（1）导电针织物线圈在受到小拉伸应变情况下，单位长度纱线电阻可认为是常数，不受拉伸变形的影响；

（2）纱线间接触电阻只与纱段的正接触力有关，并不考虑它们在交叠区域的接触长度.

2.1 导电针织物中纱线间接触力

纬平针织物及单元线圈双向拉伸受力如图2所示，其中，Fw织物是沿织物纵行方向作用在宽度lw上的织物张力，Fc织物是沿织物横列方向作用在宽度lc上的织物张力，Tw与Tc分别为纱线沿圈柱及沉降弧水平段方向的张力，Fw与Fc分别为1个单元线圈在纵行（两根圈柱）及横列方向上的张力，Ft为纱线间接触力，w为圈距，c为圈高，θ为圈柱与水平方向夹角.

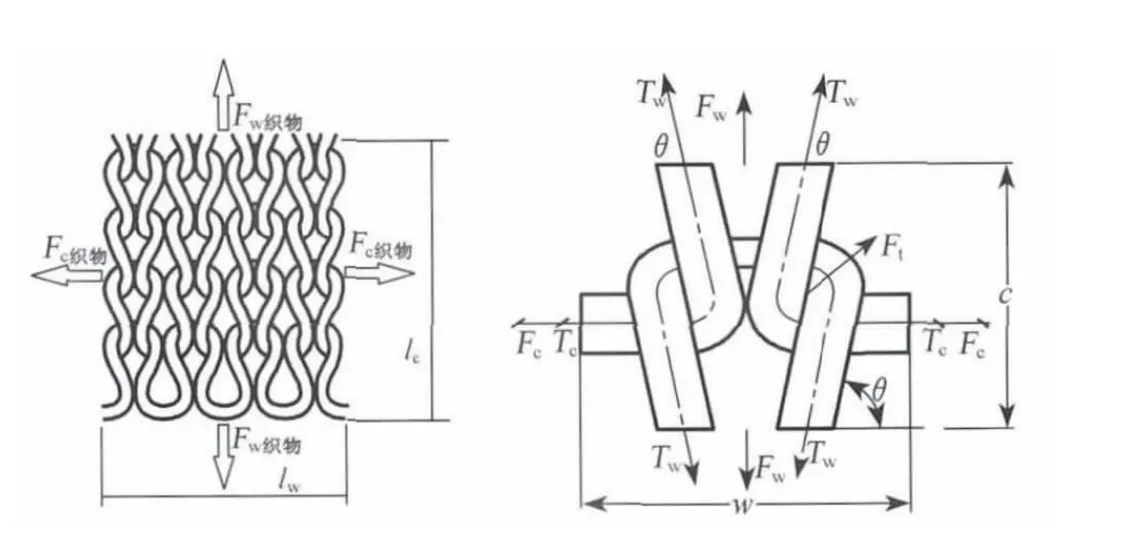
图2 纬平针织物及单元线圈双向拉伸受力图Fig.2 Biaxial tension of weft plain knitted fabric and unit loop

从织物应力定义可得

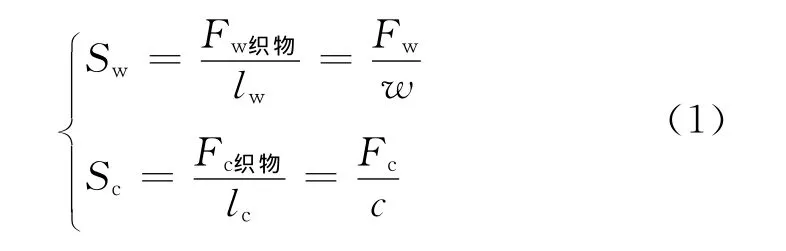
其中：Sw为织物沿纵行方向应力；Sc为织物沿横列方向应力.

由图2（b）可得

综合式（1）和（2）可得

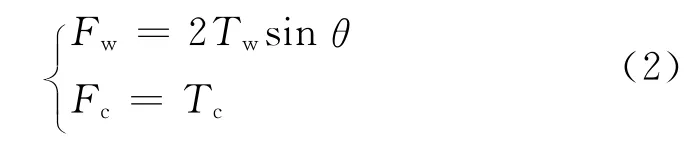
由 Kawabata模型[6]可得

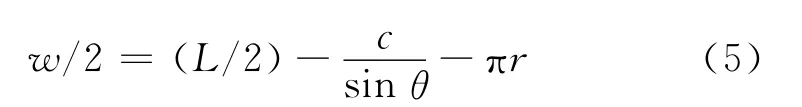
其中：r为纱线半径；L为线圈长度.

假设μ是纱线间摩擦因数，由Popper模型[1]和Kawabata模型[6]可得

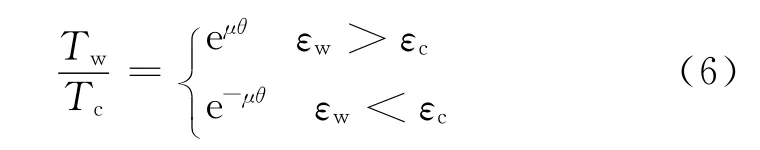
其中：εw为织物沿纵行方向应变；εc为织物沿横列方向应变.

综合式（4），（5）和（6）可得

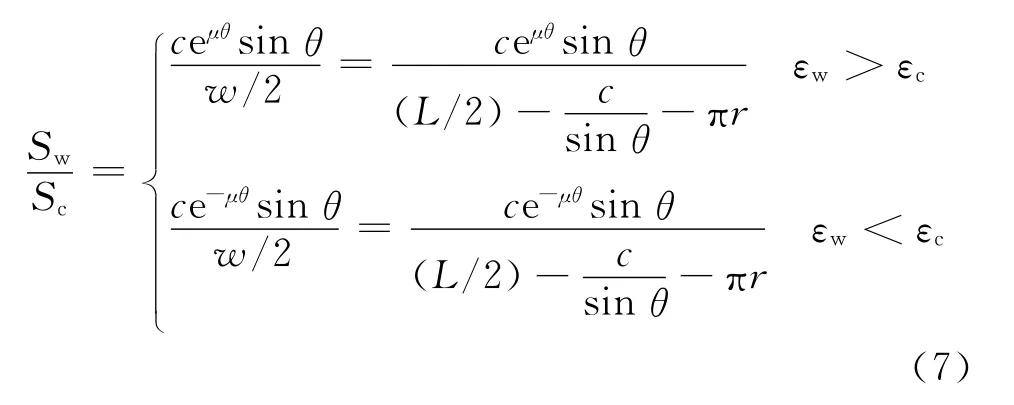
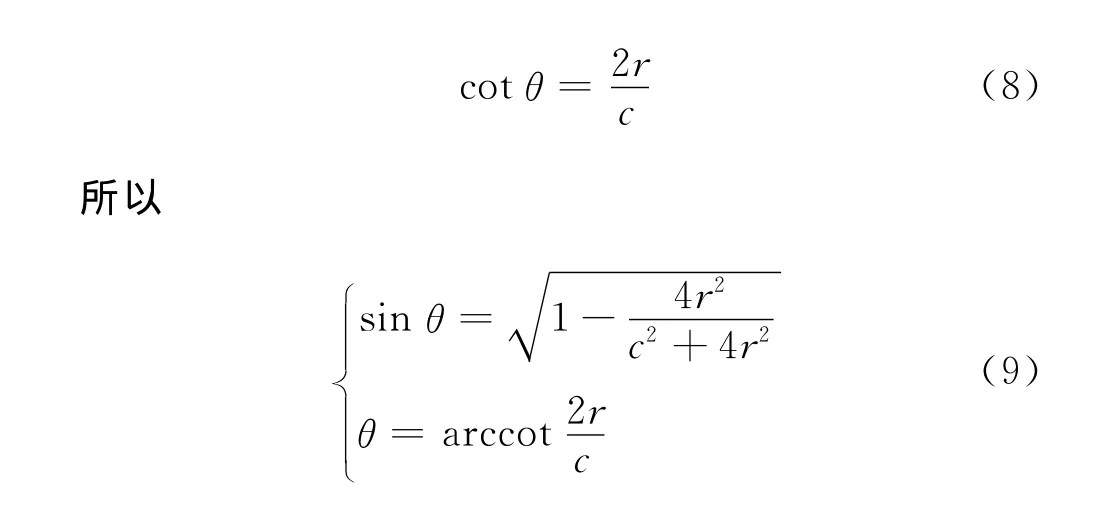
纱线倾斜角度θ可由式（8）表示为

综合式（7），（8）和（9）可得

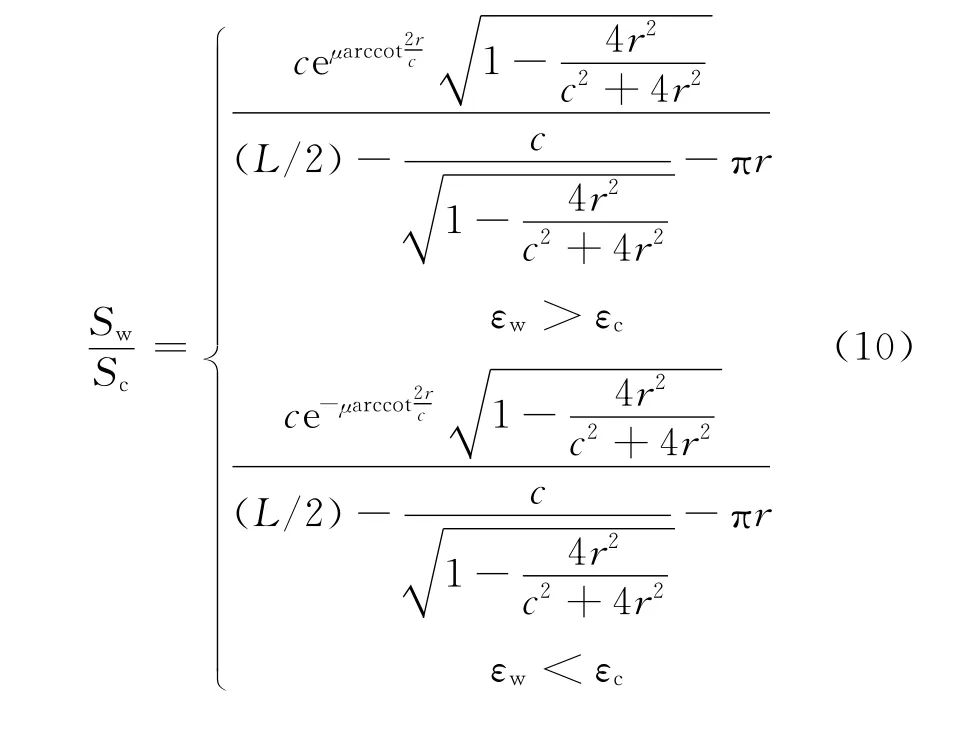
由Kawabata模型[6]可得纱线间接触力Ft

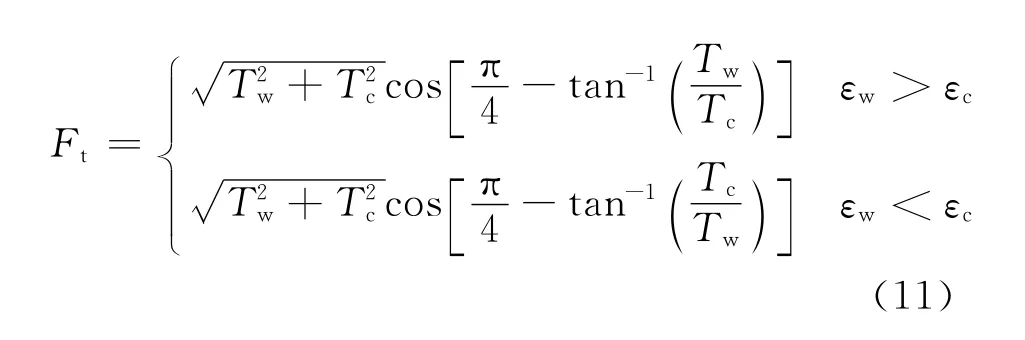
综合式（1），（2），（6）和（11）可得

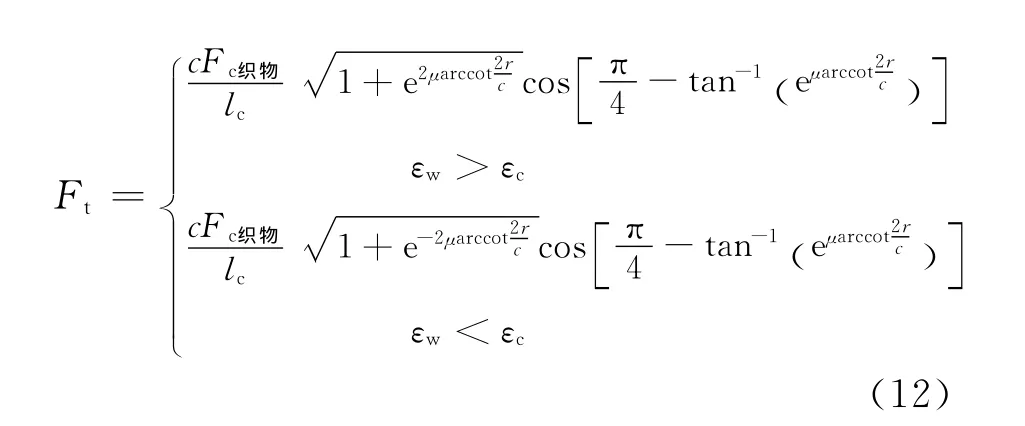
如果已知Sw和Sc以及针织物结构参数，求解式（1）和（12）分别可得Fc织物和Ft.

2.2 接触电阻与接触力的关系

针织物中接触力区域的受力分析如图3所示.为了简化计算过程，采用两个弯曲的纱线相互钩套来模拟导电针织物线圈中相互交叠的纱段.试样用一对夹子夹持，两端采用速度为0.1mm／min的定速拉伸，且加载张力为0～1N.试验中两个相互钩套的纱线受力分析如图4所示.

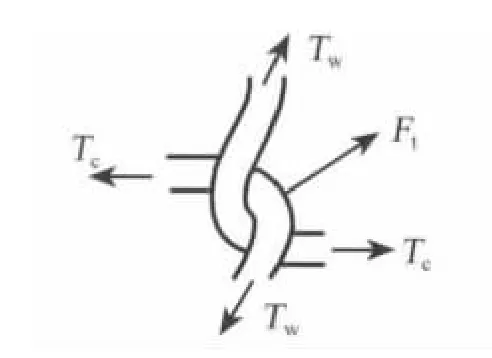
图3 针织物中接触力区域受力分析Fig.3 Tension analysis of contacting region in a knitted fabric

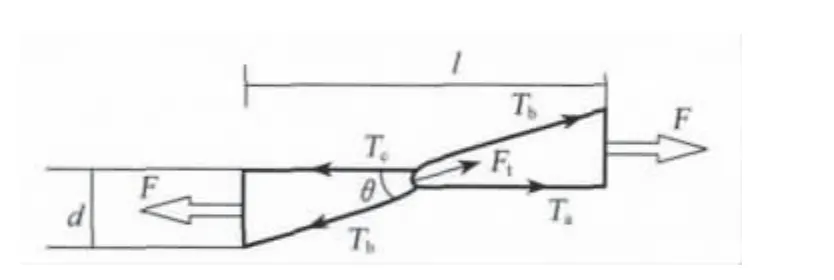
图4 两个相互钩套的纱线受力分析Fig.4 Tension analysis of two interlooped yarn

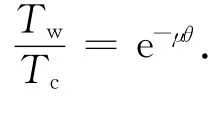
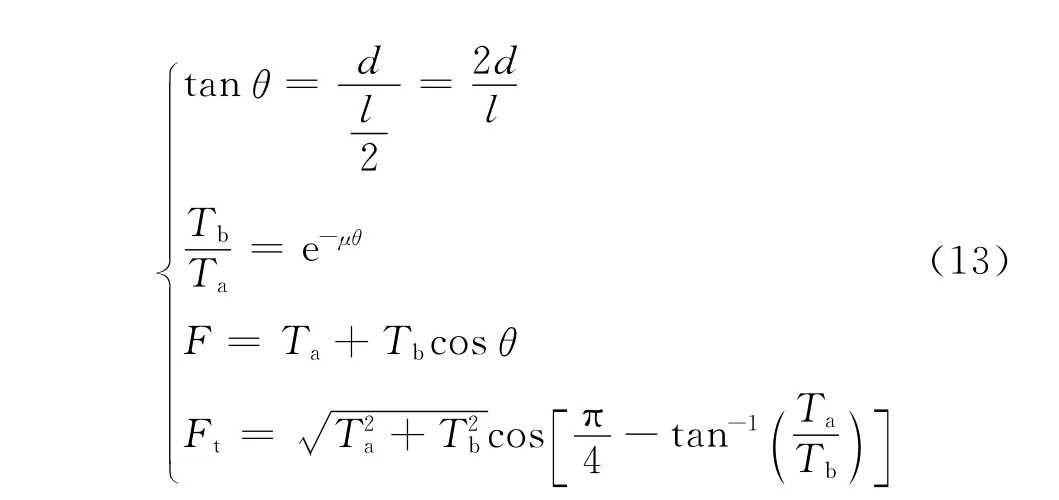
求解式（13）可得

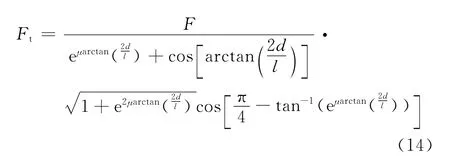
相互交叠的纱线两端点的拉伸张力与应变的关系用KES纱线拉伸仪测量；纱线间接触力与试样两端点加载张力F的关系由式（14）获得，综合以上分析可得纱线间接触力与应变的关系.通过拉伸试验，可以得到图5（a）所示的加载张力与伸长量的关系曲线，经式（14）计算得到图5（b）所示的接触力与伸长量的关系曲线.

相互交叠的纱线两端点的电阻与应变的关系用Keithley 2400型万用电表测得.纱线间接触电阻为试样两端电阻减去纱段自身电阻.通过试验可以得到图6所示的接触电阻与伸长量的关系.

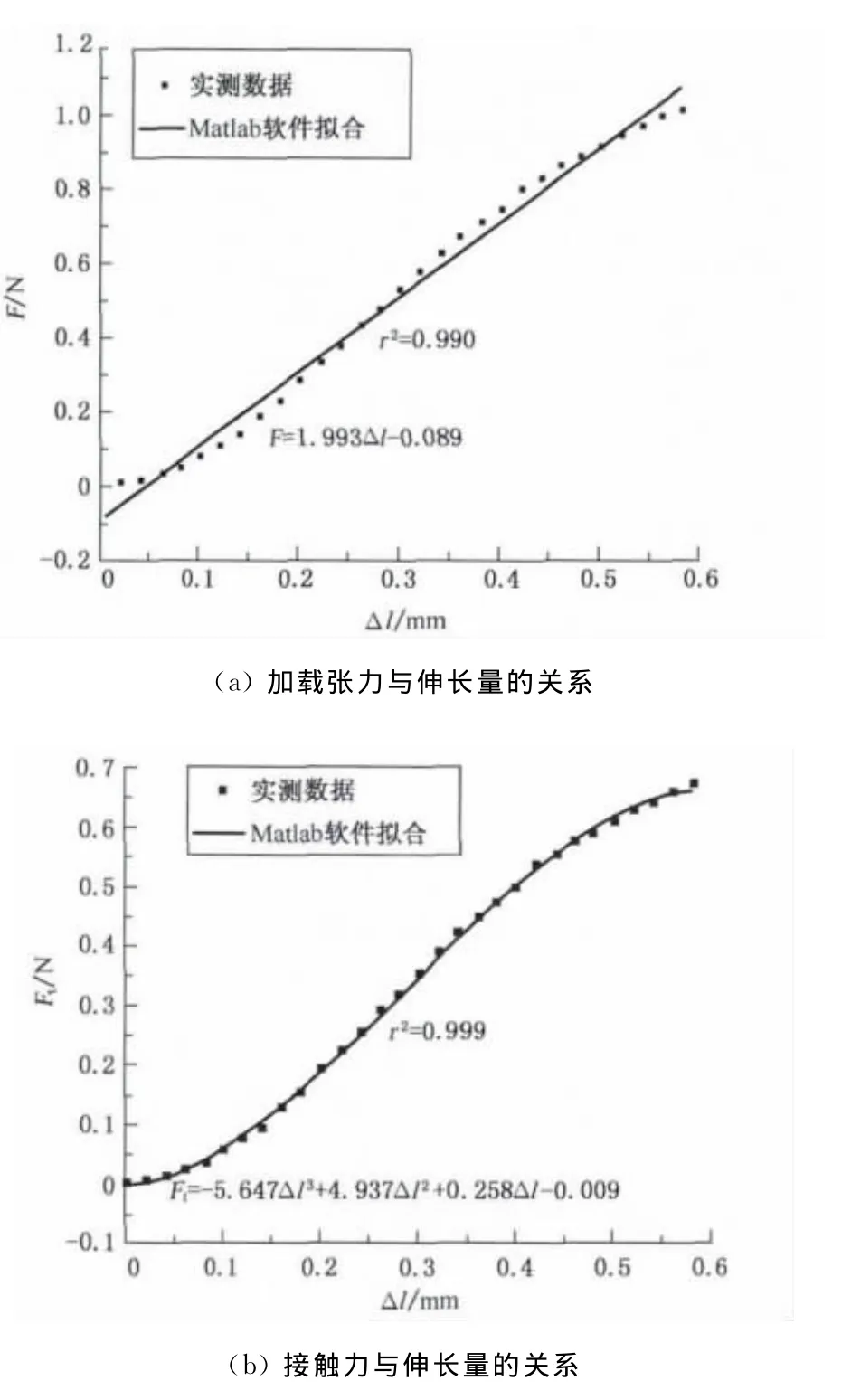
图5 加载力及接触力与伸长量的关系Fig.5 Relations between load force，contact force and elongation

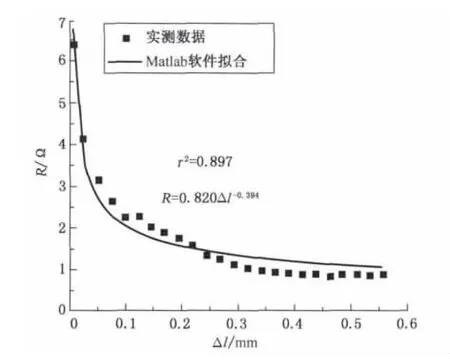
图6 接触电阻与伸长量的关系Fig.6 Relation between contact resistance and elongation

因此，综合图5和6的分析可得接触电阻R与接触力Ft之间的关系如图7所示.由图7可知，接触电阻R随接触力Ft的增加而呈幂函数减小，即R＝0.940F－0.264t，此曲线可以分为两个部分，接触力小于0.050N的“急速减小”阶段和接触力大于0.050N的“缓慢减小”阶段，这是由于在第一阶段镀银导电纱之间接触面有较大幅度的增长.的二维模型更复杂.此外，模型假设两个重叠的纱线接触电阻只与交叠部分的接触力有关，而并不考虑其接触长度，然而，大张力载荷拉伸时接触长度会变短，这可能影响模拟结果.另外，由于在大张力载荷下，纱线会伸长，纱线的电阻会随之增大，因此模拟数据小于试验值.

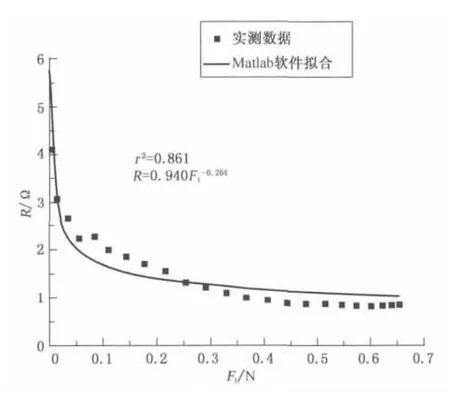
图7 接触电阻与接触力的关系Fig.7 Relation between contact resistance and contact force

如果两个接触材料是点对点的接触（如球与球、球与平面和柱状与柱状），则m＝0.5；如果两个接触材料是线对线接触（如柱状与平面），则m＝1.因为镀银导电纱是柱状结构，所以本文采用m＝0.5拟合，由此得到图8所示的拟合曲线.模型所得电阻值在一定范围内与试验数据吻合，模拟值比试验值小0.947.这是因为针织物线圈的三维结构比模拟纱线

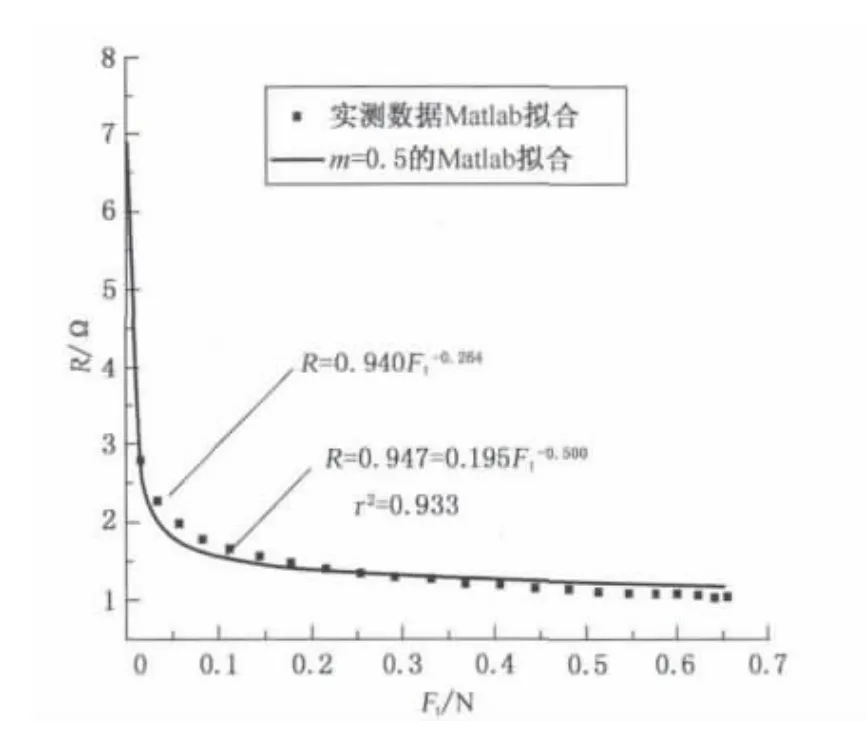
图8 经验公式拟合接触电阻与接触力的关系Fig.8 Relation between empirical equation fitting contact resistance and contact force

2.3 试样电阻与应变的关系

本文采用的导电针织物试样是由镀银锦纶丝编织而成，镀银锦纶丝的电阻率为0.516Ω／mm，试样的纵密为60横列／5cm，横密为75纵行／5cm.

当宽度lw为10cm，长度lc分别为4.0，4.5和6.4cm的导电针织物电阻与拉伸应变的关系，如图9（a）所示；当长度lc为4cm，宽度lw分别为2.5，5.0和10.0cm的导电针织物电阻与拉伸应变的关系，如图9（b）所示.图9中方点、圆点和三角点分布为实测数据，实线是由Matlab软件拟合所得曲线.当导电针织物拉伸应变在10%以内时，其电阻几乎是线性减小的，所以本文运用线性方程来拟合.由图9可知，不同横列数但相同纵行数的导电纱线针织物电阻有相同的减小趋势，不同纵列数但相同横列数的导电纱线针织物电阻也有相同的减小趋势；织物电阻随横列数的增加而减小并随纵列数的增加而增加；当导电纱线针织物受到小应变拉伸时，接触电阻在导电纱线纬平针织物电阻中发挥着重要作用.

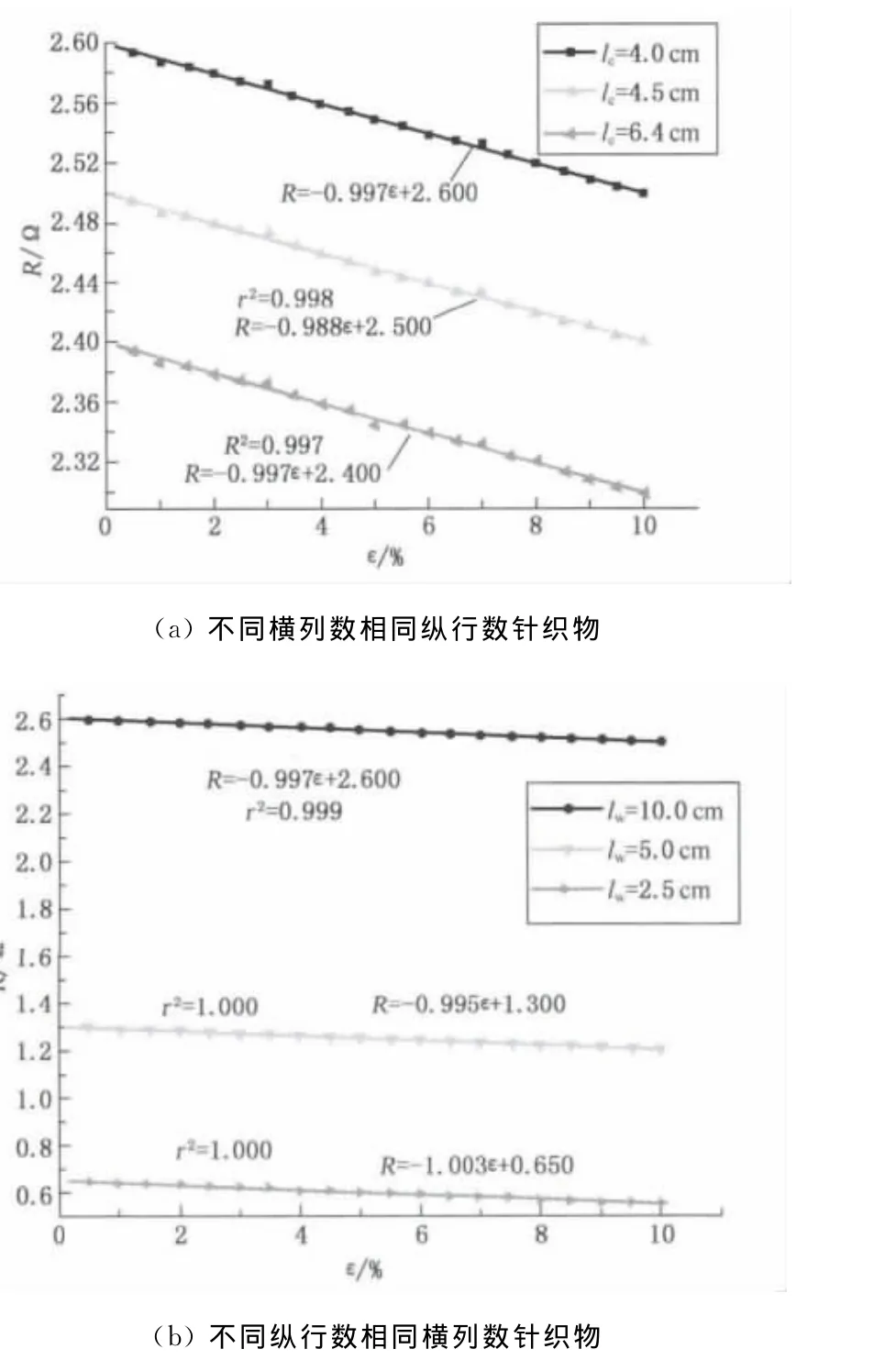
图9 在应变10%内导电纬平针织物电阻与应变的关系Fig.9 Relations between resistance and strain of conductive weft knitted fabrics within 10%strain

3 结 语

本文根据导电纬平针织物的线圈结构分析其电阻，如果只考虑接触电阻的影响，其等效电阻和拉伸应变的关系可由实验和经验公式获得.导电针织物的等效电路是综合串联和并联的复杂电路网.采用Popper和Kawabata针织物力学模型分析拉伸情况下线圈交叠纱线间接触力，为了简化接触力的计算，由两个弯曲的纱线相互钩套来模拟导电针织物线圈中相互交叠纱段.导电纱线间的接触电阻和接触力的关系可用经验公式求得.从理论分析和试验研究可得，接触电阻随接触力的增加而呈幂函数减小，由接触电阻引起的电阻变化是影响导电纬平针织物柔性传感器灵敏度的关键因素，其电阻随应变的增大而线性减小.此外，线圈转移、织物结构和纱线伸长也会影响导电纱线针织物传感器的性能.

参 考 文 献

[1]POPPER P.The theoretical behavior of a knitted fabric subjected to biaxial stresses [J].Textile Research Journal，1966，36（2）：148-157.

[2]WHITENEY J M，EPTING J L.Three-dimensional analysis of aplain knitted fabric subjected to biaxial stresses[J].Textile Research Journal，1996，36（2）：143-147.

[3]MACRORY B M， MCNAMARA A B. Knitted fabrics subjected to biaxial stress：An experimental study[J].Textile Research Journal，1967，37（10）：908-911.

[4]SHANAHAN W J，POSTLE R A.Theoretical analysis the tensile properties of plain-knitted fabrics：Part I The loadextension curve for fabric extension parallel to the course[J].Journal of the Textile Institute，1974，65（5）：200-212.

[5]HEPWORTH B.The biaxial load-extension behavior of a mode of plain weft-knitting：Part I [J].Journal of the Textile Institute，1978，69（4）：101-107.

[6]KAWABATA S.Nonlinear mechanics of woven and knitted materials[M]／／ CHOU T W，KO F.Textile Structural Composites.Amsterdam：Elsevier，1989：67-93.

[7]WU W L，HIROYUKI H，ZENICHIRO M.Computer simulation of the deformation of weft-knitted fabrics for composite materials[J].Journal of the Textile Institute，1994，85（2）：198-214.

[8]WILLIAM M M，WILLIAM R M.The bonded electrical resistance strain gage：An introduction[M].London：Oxford University Press Inc，1992：5-10.

[9]MUNDEN D L.The geometry and dimensional property of plain-knit fabrics[J].Journal of the Textile Institute，1959，50（7）：448-471.

[10]POSTLE R，MUNDEN D L.Analysis of the dry-relaxed knitted loop configuration[J].Journal of the Textile Institute，1967，58（8）：329-365.

[11]HOLM R.Electric contacts [M].New York：Springer-Verlag，1967：7-19.