Research of Multiagent Coordination and Cooperation Algorithm

Jun Li，Wen-Long Song，Yu-Rong He

(1.College Mechanical and Electrical，Northeast Forestry University，Harbin 150040，China;2.School of Energy Science and Engineering，Harbin Institute of Technology，Harbin 150001，China)

1 Introduction

In multiagent system，the interests of every agent are not the same.There will be conflicts with agents even though they accomplish the same task together.Therefore，the agent can take their actions according to the present state and the actions of others，and the final state is optimal equilibrium state which is recognized by all participants.The optimal equilibrium is Nash equilibrium of players to the present state.The game theory proves that any game has its Nash equilibrium solution，and then multiagent system must have the optimal solution.Artificial intelligence techniques overcome conventional model based approaches for the design of control algorithms［1－3］.Specifically，reinforcement learning(RL)methods［4］have been successfully applied in control applications［5－10］.Based on the game theory and reinforcement learning technology，many researchers have presented many methods.Littman introduced Minimax-Q algorithm of two-person zero-sum games［11］.Nash-Q algorithm of two-person general zero-sum games can be found in Ref.［12］.The non-zero-sum Markov games were adopted as a framework for multiagent reinforcement learning，and the learning model and learning algorithms of the metagame reinforcement learning were brought forward［13］.Q-learning from original single agent framework was extended to non-cooperative multiagent framework，and the theoretic framework of multiagent learning was proposed under general-sum stochastic games with Nash equilibrium point as learning objective［14］.However，there are amount of nonlinear equations calculation to obtain the generalsum stochastic games with equilibrium.Although Ou proved the convergence under certain restriction，the algorithm has not been applied to practical problems.So these methods can not be fit for large-scale multiagent system.

In this paper，an indirect approach is presented to seek the equilibrium solution of Markov game.Firstly，the Markov game is broken down into a sequence of state games which are independent.We need to find out the optimal equilibrium of every partial state game，and then these equilibrium games are merged on the basis of a chronological account of partial state games.The interest of pursuit group is the same in multiagent pursuit problem.The process of predator agents coordination is similar to the process of pure cooperative game.Therefore，we choose the pursuit problem to study multiagent coordination strategy based on Markov game.

2 Markov Games

In multiagent system，agent can take their actions according to the present state and the actions of others.In most cases the process of game is not over until so much is being done by agents.That is multistage game.Markov games are the modal multistage game.

Definition 1Pursuit problem Markov model:It is a tuple＜n，S，{Ai}，T，{Ri}＞where n is the set of agents，n=Np∪Ne;Np={1，2，…，n}is the set of predators;Ne={1，2，…，m}is the prey set.S is the set of system states;Aiis the set of agent i actions;the joint action space can be expressed as A=A1×…×An×An+1;T:S×A×S→［0，1］is state transition probability and R:S×A→R is a reward function.

All of predators try their best to find out the strategy with the greatest sum of cumulative reward discount.And predators must arrive at the destination next to the prey.Only by waging it can predators get paid.The joint strategy with best interests for predators is the optimal strategy of pursuit group.

3 Multiagent Coordination and Cooperation Mechanism

The optimal strategy in dynamic environment is the only goal of pursuit group，which needs agents to forecast environment and select the actions with preference.It is reinforcement learning that can complete preference action selection according to the environmental reward.All of agents optimize decision processes at the same time，and then it will not lead to convergence if other agents are regard as a part of environment.Equilibrium game summarizes the characteristics of agents homeostasis in game theory.If each player has to correctly predict the behavior of other players and take rational action，the game will arrive at an optimal and stable state for all agents.

Definition 2In n-person Markov game，for k=1，2，…，n，the Q-values of Nash equilibrium for player I is the function of the state s and the joint action(a1，…，an).We can explain that it is the sum of reward discount for player k when the games start from the state s，take the joint action(a1，…，an)，and then arrive at Nash equilibrium(π*1，…，π*n)，that is:

where rkis the reward function of player k;p(s'|a1，…，an)is the state transition probability;vk(s，a1，…，an)is the reward of player k;γ∈［0，1)is the discount factor.In this paper，we use the tabular method to solve multiagent pursuit problems.According to Nash equilibrium definition，the Q-values can be updated by Eq.(1)

where(π1，…，πn)is Nash equilibrium game of multiagent system andαt∈(0，1］is an appropriate learning rate.Here，except for rtk and st+1，we need the strategy valueπj(j≠k)prior knowledge of other agents to update the Q-values.Here，we uses the method of probability and statistics and Bayes formula to estimate the other policy knowledge［15］.

We assume that proi(s，j，ak)is the confidence degree for agent i to agent j under the state s，and agent i always assumes that agent j takes akaccordance with proi(s，j，ak).The initial value of proi(s，j，ak)takes the Dirichlet distribution，it is followed as Eq.(2)

After every agent takes their actions，agent i observes the new state s'and other agents’actions，then to revise proi(s，j，ak).According to the Bayes formula，

where p(s'|aj，ai)denotes the state transition probability after agent i and agent j takes the joint action to the state s'，which can be got from environment knowledge.p(s'|ai)denotes the state transition probability after agent i taking the single action to the state s';p(aj)can be replaced of proi(s，j，ak).proi(s，j，ak)can be updated by modifying the parameter Nkjon the basis of akof agent j.

In Q-values table，the columns represent the joint action policy of other agents(not including agent i)while the rows represent the overall action policy of agent i，and therefore the joint action probability figured as:

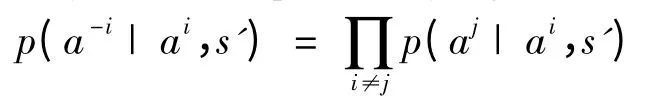
It is a repeated game learning model between agents.We can assume that every agent can take other agents’actions，and the agent chooses its optimal respond action by the probability estimation of other agents’actions.When the game is over，the agent can observe other agents’actions to revise their confidence.

4 Revising the Game Results

Because proi(s，j，ak)is used to calculate the joint action probability p(a－k|ak，s')，which impacts the results of updating Q-values.In this paper，we use relative mean deviation to evaluate the confidence of proi(s，j，ak).Then we can filter the actions forecasting with low confidence of proi(s，j，ak)to improve the game course.E is the value of relative mean deviation，and its fitting equation is as follows:

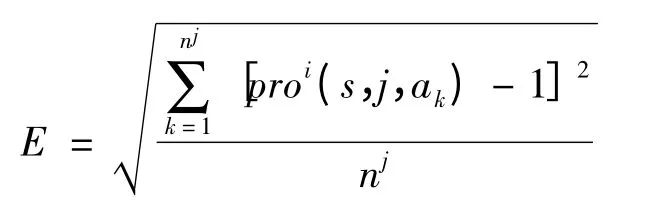
where njis the number of action types that agent j can choose under any states.Therefore，the confidence of proi(s，j，ak)is determined:

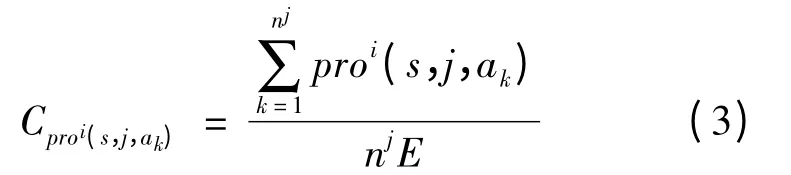
Obviously，there is

Eq.(3)can be modified to

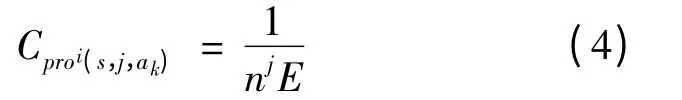
In order to guarantee the reliability of proi(s，j，ak)，Eq.(4)should satisfy a certain threshold，which is Cproi(s，j，ak)∈［α，β］，α，β≥0.5.It can ensure the effectiveness of games and reduce the number of trial and error to speed up the games speed.

5 Experimental Setting and Simulation Results

To evaluate the approach proposed in this paper，we perform the simulation experiments on pursuit problems under different situation.

5.1 Description of Convergence

Fig.1 shows the sketch map of the first simulation experiment:(a)is the initial state and(b)is the object state.There are six predators and two preys in a 15×15 grid square.The black solid round stands for a predator and the white one stands for a prey.Predators and preys can move to one of its adjacent four cells or remain on its current position.If the predator moves out of the boundary or get collided with other agents，it must stay it initial position next t.We use the parameter as:each predator i receives a reward Ri=200 when it helps to capture the prey and a negative reward of－50.0 when it collides with another predator，when an predator moves to the prey with other predators supporting which makes the prey captured，the reward is 1000.In all other cases the reward is－5;γis 0.95 andαtis 1.

Fig.1 Pursuit problem in grid-model

The results of 2500 experiments are shown in Fig.2.Obviously，our approach will converge to the optimal value after 1000 times of learning，which can prove the feasibility of the approach.At the same time，we should also pay attention to the curve at 250－1000 times experiments.It is not smooth and the learning process is iterative.It is the reason that predators are influenced by the environment.It takes much more time for agents to learn the action strategies near obstacles.

Fig.2 Sketch map of pursuit time steps

5.2 Effects of Different Exploration Strategies

With the experimental parameters unchanged，a pursuit situation is designed in Fig.3.Four predators chase a static prey.We compare the effects of three exploration strategies on the game results.They areεgreedy，Boltzman and weighted Boltzman exploration strategies.As shown in Fig.4，with the development of learning，the path length to capture the prey is gradually shortened;finally the three methods can converge to the optimal value(58)of the model.In contrast，the weighted Boltzman exploration strategy is much better than the other two.It uses the maximum Q-values Max Q(ai)=maxQ(π－i，ai)to revise the original value of ai.It is the joint action value of all agents，which is helpful to choose the optimal equilibrium for agents.Because the weight of preference choice is set in advance choice weighted to shorten the time of games.Theε-greedy exploration strategy choose the action with the maximum reward，which easily leads to fall into the local optimal values，consequently its convergence speed is the slowest.

Fig.3 Pursuit problem in grid-model

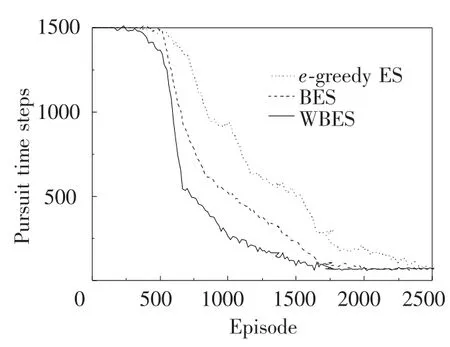
Fig.4 Results of different exploring strategies

5.3 Testing the Agent Mobile Trace

The experiment setting is the same with 4.2.As shown in Fig.5，we apply the convergent algorithm to test mobile trace of four agents in the same environment.The path length is obviously calculated on the grid number covered by agents.The results indicate that they are two different shortest paths(the optimal solution).That is，the optimal solution is not unique.Our algorithm can not be sure that agents choose the same optimal solution every time.

Fig.5 Motion trails of pursuers evolved by two different learning processes

6 Conclusions

In multiagent system，every agent can be thought as a player.The equilibrium decision of game theory can solve the convergent problem of mutltiagent reinforcement learning.We set up a Markov game model to pursuit problem.By solving the optimal equilibrium of Markov game，we can get the optimal cooperation and coordination games of multiagent.The simulation results show that evaders can be captured effectively and efficiently，and prove the feasibility and validity of the given algorithm.However，our algorithm may get different optimal equilibrium，which does not study on consistency problem in group decision making.

［1］Catalin B，Cristian V，Octavian A.Development of membrane controllers for mobile robots.Information Sciences，2012，187(3):33－51.

［2］He J J，Gu H，Wang Z L.Multi-instance multi-label learning based on gaussian process with application to visual mobile robot navigation.Information Sciences，2012，190(5):162－177.

［3］Rubio J J，Torres C，Aguilar C.Optimal control based in a mathematical model applied to robotic arms.International Journal of Innovative Computing，Information and Control，2011，7(8):5045－5062.

［4］Sutton R，Barto A G.Reinforcement Learning I:Introduction.Cambridge:MIT Press，1998.

［5］Hwang K S，Lin H Y，Hsu Y P，et al.Self-organizing state aggregation for architecture design of Q-Learning.Information Sciences，2011，181(13):2813－2822.

［6］Vien N A，Yu H，Chung T C.Hessian matrix distribution for bayesian policy gradient reinforcement learning.Information Sciences，2011，181(9):1671－1685.

［7］Cheng X，Shen J，Liu H，et al.Multi-robot cooperation based on hierarchical reinforcement learning.Lecture Notes in Computer Science，2007，4489:90－97.

［8］Mataric M J.Reinforcement learning in the multi-robot domain.Autonomous Robots，1997，4:73－83.

［9］Xiao H，Liao L，Zhou F.Mobile robot path planning based on Q-ANN.Proceedings of the IEEE International Conference on Automation and Logistics.Piscataway:IEEE Press，2007.2650－2654.

［10］Zhou C J.Robot learning with GA-based fuzzy reinforcement learning agents.Information Sciences，2002，145(1－2):45－68.

［11］Littman M.Markov games as a framework for multi-agent reinforcement learning.Proceedings of the Eleventh International Conference on Machine Learning.New Brunswick，NJ:Morgan Kaufman，1994.157－163.

［12］Hu J，Wellman M.Multiagent reinforcement learning:theoretical framework and an algorithm.Proceedings of the Fifteenth International Conference on Machine Learning.San Francisco，CA:Morgan Kaufman，1998.242－250.

［13］Gao Y，Zhou Z H，He J Z，et al.Research on Markov game-based multiagent reinforcement learning model and algorithms.Journal of Computer Research＆Development，2000，37(3):257－263.

［14］Ou H T，Zhang W D，Xu X M.Multi-agent learning based on general-sum stochastic games.Acta Automatica Sinica，2002，28(3):423－426.

［15］Li J，Pan Q S.A multiagent reinforcement learning approach based on different states.Journal of Harbin Institute of Technology(New Series)，2010，17(3):419－423.