Research on Two-Step Hydro-Bulge Forming of Ellipsoidal Shell with Larger Axis Length Ratio

Shi-Jian Yuan，Lan Hu，2，Zhu-Bin He，Bu-Gang Teng，Zhong-Ren Wang

(1.National Key Laboratory of Precision Hot Processing of Metals，Harbin Institute of Technology，Harbin 150001，China;2.Shanghai Aerospace Equipments Manufacturer，Shanghai 200245，China)

1 Introduction

The spherical shells and ellipsoidal shells are used increasingly in industry as water tanks，pressure vessels，containers，artistic objects，and components of special structures due to the advantages of the small wind area，the large capacity and the attractive outline.However，they are very difficult to be manufactured by using conventional processes.A traditional method for manufacturing ellipsoidal shells is stamping，in which petals are formed using dies and a press，and then assembled and welded into an ellipsoidal shell.On one hand，large-scale press and multiple die sets are usually needed because the curvature is changed from one point to another;on the other hand，precise cutting of curved blanks is difficult and many calibrations are needed.Therefore，higher costs and a longer produce period are usually unavoidable.Comparing with the traditional process，the integral hydro-bulge forming(IHBF)technology provides a more easy，economic and flexible way to manufacture spherical and ellipsoidal shells［1－7］.The process has a very strong flexibility towards the change of the shell dimensions;the cost is very low，because no presses and dies are needed.However，the direct integral hydro-bulge forming technology can only be used for manufacturing the ellipsoidal shell with a smaller axis length ratio.

The hydro-bulge forming of ellipsoidal polyhedron shells without constraint in short axis direction has been extensively researched［8－14］.It is found that difficulties arose when the axis length ratio increases.Fig.1 shows an ellipsoidal shell revolving along the y-axis and the characteristic dimensions.a and b are the lengths of the long axis and short axis respectively;the axis length ratio m equals a/b;φis the intersection angle between the shell normal and the rotating axis.It is shown by experiments that the short axis is elongated as the internal pressure increases，thus the axis length ratio can be obviously decreased.When the axis length ratio exceeds a critical value，the wrinkling usually occurs at the equator at the early stage of hydro-bulge forming［11－12］.It is found that for an ellipsoidal polyhedron shell under pressurizing，a critical value m0=exists.When m＞m0，the latitudinal(circumferential)stress at the equator area is in a compressive state.The wrinkling can take place in this area，and the weld can be bulged out of the shell surface，which is very difficult to eliminate with higher pressure values.When 1＜m≤m0，the latitudinal stress at the equator area is in a tensile state，and the shell is subjected to biaxial tensile stresses.The wrinkling cannot occur and the polyhedron shell can be bulged into the ellipsoidal shell successfully［2，13－14］.Fig.2 presents the diagram of the latitudinal stress versus axis length ratio m and position angleφ［2］.The latitudinal stress at the equator area changed to compressive as the axis length ratio exceeded

In the current paper，the two-step hydro-bulge forming technology is proposed to solve the problems encountered in hydro-bulge forming of ellipsoidal shell when the axis length ratio is larger thanExperiments and numerical simulations are carried out to study the plastic deformation pattern，the wrinkling and the latitudinal stress variation，and thickness distribution，with the axial constraint.

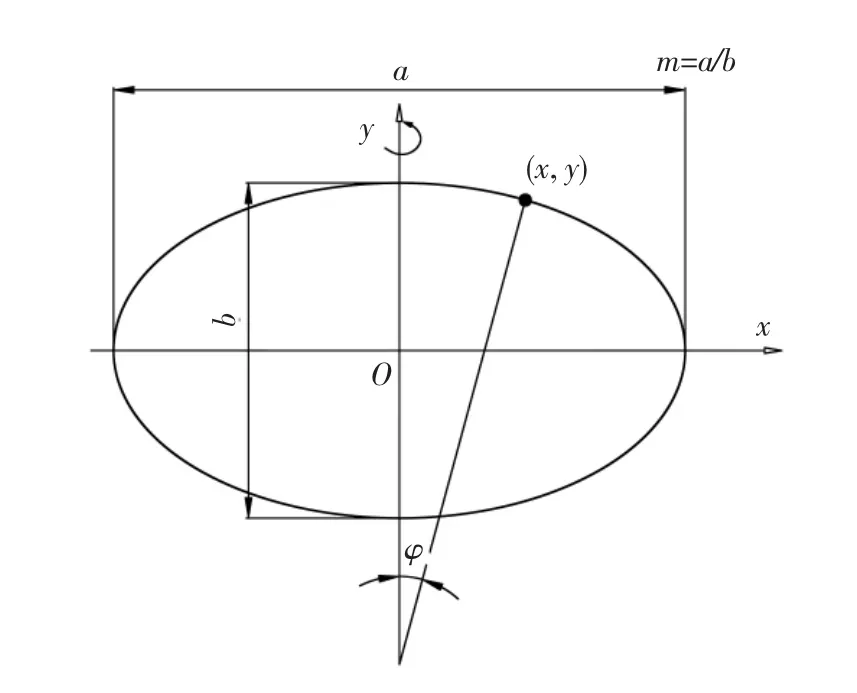
Fig.1 Characteristic dimensions of ellipsoidal shell

^Fig.2 Diagram of latitudinal stress versus axis length ratio m and position angleφ

2 Materials and Method

2.1 Assembly of Ellipsoidal Polyhedron Preform

The raw materials utilized in the investigation consisted of lateral petals，a central tube and two polar flat plates.Every lateral blank was cut according to the developed drawing of the polyhedron shell，and then roll-bent into a single-curvature petal［11］.The GTAW(gas tungsten arc welding)was used to assemble the petals and the central tube together.The lateral petals were firstly assembled by tack welding at several points to form the contour of the polyhedron preform，and then all the gaps of the structure were connected.Fig.3 shows the ellipsoidal polyhedron preform used in the experiment.It had 16 lateral petals and its initial axis length ratio was m=2，which was much larger than the critical value m0.The length of the long axis of the ellipsoidal polyhedron preform was designed as 1000 mm，whereby the length of short axis was 500 mm.The petals and the central tube were both made of carbon steel 1020.The initial wall thickness of the petal was 1 mm，whereby the central tube had a wall thickness of 8 mm，outer diameter of 219 mm and length of 520 mm.The yield strength and tensile strength were 225 MPa and 480 MPa respectively.The strain-hardening exponent was 0.25.

Fig.3 Assembly of ellipsoidal polyhedron preform

2.2 Process of Two-Step Hydro Bulge Forming of Ellipsoidal Shell and Comparison with Direct Hydro-Bulge Forming

The new two-step manufacturing process for producing ellipsoidal shell includes:(a)hydro bulge forming the polyhedron preform with the axial constraint，(b)replacing the central tube with two flat polar blanks after the first step of hydro-bulge forming process;(c)the ellipsoidal shell with flat polar blanks pressurized again to obtain a smooth surface.Water was firstly filled into the polyhedron structure at the beginning of each step，and then pressurized with a pump，with a slow pressuring rate(around 0.2 MPa/min).The polyhedron preform would endure the wrinkling at lower pressures and unfolding of the wrinkles at higher pressures.After the first step of hydro bulge forming，two circular plates made of carbon steel 1020 with a diameter of 290 mm and a thickness of 1 mm were used to replace the central tube.In the second step of hydro bulge forming，the ellipsoidal shell was pressurized to 1.2 MPa to form a smooth contour.

The sectional drawings of hydro-bulge forming of ellipsoidal shells with and without the axial restriction are shown in Fig.4，where p is the internal pressure.As can be seen in Fig.4(a)，the difference between the vertical sectional area(πab/4)and horizontal sectional area(πa2/4)is very large，and the resultant force along the vertical direction is much bigger than that along horizontal direction under a uniform pressure.Therefore，to satisfy the system balance，the difference between two sectional areas is about to decrease.Thus，the short axis of the ellipsoidal shell would be elongated，accompanied by the large shrinkage of the long axis.This can be referred to as the spherical tendency of the ellipsoidal shell under pressurizing.It is greatly possible that the shrinkage of the long axis inevitably causes the severe wrinkling.However，after applying the axial constraint(Fig.4(b))，the deformation modes of the ellipsoidal shell are dramatically changed.The central tube balances a part of the vertical resultant force and the growth of the short axis is restricted by using the central tube.The long axis would still be shrunk，but its degree is obviously reduced.

Fig.4 Deformation patterns of hydro-bulge forming of ellipsoidal shell

2.3 Finite Element Model

In order to describe the plastic deformation patterns of ellipsoidal shells with axial constraint，numerical simulations were preformed using ABAQUS/Explicit.Due to geometry and loading symmetries，only a half FE model was adopted in the simulations，as shown in Fig.5.The lateral petals and the central tube were both modeled by using S4R elements(a 4-node quadrilateral shell with reduced integration)，with a mesh size of 8 mm and five integral points along the thickness direction.The material model used for the shells were homogeneous and isotropic elasticplastic material following the Mises yield criterion.The welds in this investigation are simplified as follows:the intersection between the petal and the tube was tied together，whereby the welds between the petals were considered as lapped joints.No pre-applied stress is taken into account.Symmetry boundary conditions were created at the equator.Moreover，a linear loaded internal pressure was applied to the inner surface of the ellipsoidal shell.

Fig.5 FE meshes for ellipsoidal polyhedron preform

3 Results and Discussion

3.1 Experimental Results

As discussed in Section 2.2，the wrinkling is still likely to occur with the axial constraint，but the degree would be largely reduced.While the pressure reached 0.3 MPa，wrinkles started to occur at the lateral welds.The weld was bulged out of the shell surface clearly，as shown in Fig.6.When the pressure was above 0.8 MPa，the temperate zone began to expand and the wrinkling was alleviated gradually as the pressure increased.The wrinkles were unfolded under a higher level of pressure.The wrinkling phenomenon was almost removed when the pressure reached 2 MPa，as shown in Fig.7.Simultaneously，the shrinkage of the circumference at the equator was 3.5% after measuring.

Fig.6 Wrinkling occurred during first step of hydro-bulge forming process

Fig.7 Ellipsoidal shell after first step of hydro-bulge forming

After the first step of hydro-bulge forming，the central tube was removed and replaced with polar plates.Then the ellipsoidal shell was pressurized to 1.2 MPa to calibrate the shape.After the second stage，the ellipsoidal shell became smooth and the wrinkles were completely removed，as shown in Fig.8.It was noted that the calibration pressure could affect the axis length ratio in the absence of the axis constraint，thus a low pressure was adopted here.An additional shrinkage of the equator circumference in this step was measured to be 0.5%.The axis length ratio of the ellipsoidal shell was 1.8 after the second step of hydro bulging.

Fig.8 Ellipsoidal shell after two-step hydro-bulge forming

3.2 Sequence of Plastic Deformation with Axial Constraint

According to the yield criteria，as soon as the effective stress of a point reaches the yield strength of the material，plastic deformation would occur there.Fig.9 shows the expanding process of the plastic deformation in one of the lateral petals during hydrobulge forming with axial constraint.The shaded zone(dark grey)indicates that plastic deformation has occurred there.It is found that the plastic deformation firstly arises at the lateral weld when the pressure reaches 0.1 MPa(Fig.9(a))，and then expands to the areas near the pole and the equator(Fig.9(b)and 9(c)).Finally，it takes place at the temperate zone when the pressure reaches 1 MPa.The existence of the flexural effect at the lateral welds is the main cause of plastic deformation occurred early at this area［11］.

Fig.9 Plastic zone(dark gray)expansion when internal pressure reach

3.3 Wall Thickness Distribution

Fig.10 presents the wall-thickness distribution of the ellipsoidal shell at the end of the first step of hydrobulge forming when the pressure reaches 2 MPa.The maximum thinning occurs at the connected region between the petal and central tube，with a thinning ratio of 24.4%，followed by higher latitudinal areas.Multi-layered welding was applied to the connected areas between the petal and central tube in the experiments to prevent the split of these area.The wall thinning of the equator area is the lowest and the thinning ratio near the lateral weld is only 1.2%.It is also seen that the areas near the central tube are concave due to the axial restriction.To cover the concaved areas，the diameter of polar plates for the second step was chosen to be larger than the outer diameter of the central tube for the first step.

3.4 Latitudinal Stress Variation

Fig.10 Wall-thickness distribution of ellipsoidal shell after first step of hydro-bulge forming

Fig.11 Latitudinal stress distribution during first step of hydro-bulge forming

The latitudinal stress(outside surface)distribution during the first step of the hydro-bulge forming is shown in Fig.11.It is shown that the wrinkling is closely related to the compressive latitudinal stress of the ellipsoidal shell.At the early stage of bulging(0.25 MPa)，the compressive latitudinal stress is observed at the center of the petal at the equator.The maximum magnitude of the compressive stress at the equator is 259 MPa.While the pressure reaches 0.3 MPa，the instability occurs and the welds are bulged out of the surface，which agrees well with the experiments.The maximum magnitude of the compressive latitudinal stress at the equator increases to 264 MPa and the latitudinal tensile stress at the temperate zone is observed with the maximum value of 355 MPa near the weld.When the pressure exceeds 1 MPa，the areas with the compressive stress decrease with the expansion of the shell.When the pressure reaches 2 MPa，the wrinkling disappears，and the tensile latitudinal stress occupies the domain，except for the areas at the lateral weld.This is due to the unfolding of the wrinkles(flexural effect)，which changes the stress state at the outside surface from tension to compression at the lateral weld.

4 Conclusions

1)The two-step hydro-bulge forming process suggested in this paper is feasible to manufacture the ellipsoidal shells with the axis length ratio lager than

2)The central tube balances a part of axial force and changes the system equilibrium.With the axial constraint，the growth of the short axis is greatly reduced，and the deformation patterns of the ellipsoidal shell are dramatically changed.The shrinkage of the circumference of the equator after the first step of the hydro-bulge forming is 3.5% and an additional shrinkage of 0.5% occurs in the second step.

3)The wrinkling occurs in the first step of hydrobulging forming process，and it has a close relationship with the latitudinal stress distribution of the ellipsoidal shell.The compressive latitudinal stress is observed at the equator at the early stage of the first step of the hydro-bulge forming.With the increase of the internal pressure，the tensile latitudinal stress gradually dominates the top surface of ellipsoidal shell except for the equator areas near the lateral welds

4)It is predicted by the numerical simulations that the wall-thinning ratio near the joints between the petal and central tube is the largest，whereas the thinning ratio near the lateral welds at the equator is only 1.2%.The plastic deformation firstly arises near the lateral welds，and then expands to the areas near the pole and equator，and it takes place at the temperate zone finally.

［1］Zhang S H，Wang Z R，Wang T.The integrally hydroforming process of spherical vessels.Int.J.Pressure Vessels Piping，1990，42(1):111－120.

［2］Wang Z R，Liu G，Yuan S J，et al.Progress in shell hydroforming.J.Mater.Process.Technol.，2005，167(2－3):230－236.

［3］Hashemi J，Rasty J，Li S，et al.Integral hydro-bulge forming of single and multi-layered spherical pressure vessels.J.Pressure Vessel Technol.ASME，1993，115(3):249－255.

［4］Zhang S H，Jiang L，Wang B L，et al.Finite-element analysis of the integral hydrobulge forming of double-layer gap spherical vessels.Int.J.Pressure Vessels Piping，1996，68(3):161－167.

［5］Wang Z R，Zhi Y S，Zeng Y S，et al.Experimental research and finite-element simulation of plates hydrobulging in pairs.Int.J.Pressure Vessels Piping，1996，68(3):243－248.

［6］Teng B G，Yuan S J，Wang Z R.Experiment and numerical simulation of hydro-forming toroidal shells with different initial structure.Int.J.Pressure Vessels Piping，2001，78(1):31－34.

［7］Zhang S H，Wang B L，Shang Y L，et al.Threedimensional finite element simulation of the integral hydrobulge forming of a spherical LPG tank.Int.J.Pressure Vessels Piping，1996，65(1):47－52.

［8］Yuan S J，Zeng Y S，Wang Z R.The Integral hydrobulging forming of ellipsoidal shells.Proceedings of the 5th Internaltional Conference on Technology of Plasticity.Columbus，Ohio.1996.258－265.

［9］Wang Z R，Zeng Y S.Occurring and expanding of the plastic deformation in ellipsoidal shells subjected to internal pressure.Acta Mechanica Solida Sinica，1998，19(1):85－88.

［10］Wang Z R，Zeng Y S，Yuan S J，et al.The research on the plastic deformation of the hydro-bulge forming of ellipsoidal shells.Acta Mechanica Solida Sinica，1998，19(3):259－264.

［11］Zeng Y S，Wang Z R，Yuan S J.The numerical simulation of the integral hydrobulging of ellipsoidal shells.J.Mater.Process.Technol.，1997，72(3):358－362.

［12］Zhang S H，Danckert J，Wang Z R，et al.Numerical simulation of plastic deformation of pressurized oblate spheroid-inscribed single-curvature shells.J.Manuf.Sci.Eng.，2000，122(1):235－243.

［13］Zhang S H，Zeng Y S，Wang Z R.Theoretical analysis and experimental research into the integral hydro-bulge forming of oblate shells.J.Mater.Process.Technol.，1996，62(1):199－205.

［14］Zeng Y S，Yuan S J，Wang F Z，et al.Research on the integral hydrobulge forming of ellipsoidal shells.J.Mater.Process.Technol.，1997，72(1):28－31.