Impact of Online Community Structure on Information Propagation:Empirical Analysis and Modeling

Zhong He，Lian-Ren Wu，Xia Chen，Ting-Jie Lu

(School of Economics and Management，Beijing University of Post and Telecommunications，Beijing 100876，China)

1 Introduction

Rapid development of information and communication technology has increased the wide adoption of online social network in our life.Indeed，online social network，such as Sina Micro-blog，Twitter，and Facebook，has become an indispensable part of our life.Every day we sign in our homepages more than once to view and share information.These online social networks have common characteristics:instantaneity，simplicity and universality.Sina Microblog is taken for example.Unlike the traditional blog［1］，it allows the use of mobile devices to disseminate information by a length of 140 characters text anytime and anywhere.Investigating the online social network is crucial in a broad range of settings from information propagation，viral marketing to political purposes.

In recent years，online social network as a platform for the dissemination of information has been widespread concern.Cha and his colleagues collected the traces of photos propagated in Flick and tried to explore how far a photo would spread and the role of the friendship in the diffusion［2］.Their results showed that in Flickr，it was hard for a photo to propagate widely，even for the popular ones.Yang and Leskovec developed a linear influence model to model the information propagation in online social media by predicting which node would influence which other nodes in the network［3］.Furthermore，there are studies which have a focus on the impact of network topology structure on the information propagation［4－5］.An inspiring work［6］:it was found that in a mobile communication network if the weak ties were removed gradually there would be a phase transition in the network.

Online social networks not only have the characteristics of instantaneity，simplicity，and universality，but also the more important one is that it provides a huge platform for human interaction.Human interaction in online social networks generates online communities［7］.Networks with a community structure，or group networks，are common to many social and economic phenomena.Within the community，each individual is directly connected to most other individuals，but connections among different communities are relatively rare［8－9］.Many scholars have studied how community structure influences epidemic spread in social networks.For example，Wu and Liu presented a model with both an adjustable clustering coefficient and an adjustable degree of community.They found that the efficiency of epidemic spreading in this model depends mainly on the degree of community and decreases with the increase of the degree of community［10－11］.Huang and Li studied the epidemic spreading in scale-free networks with community structure［12］.For the information propagation in online social network，Tang et al.studied two tightly coupled topics in online social networks:relationship classification and information propagation［13］.They evaluated their approach with large scale real-world data from Renren network，showing that the performances of relationship classification and propagation maximization algorithm are pretty good in practice.

So far，we do not know how communities structure in online social network affect the range and velocity of information propagation.Here our goal is to solve this question.

2 Empirical Analysis

In this paper，we use the data collected from a social networking service site named Renren Network.It is a popular communication platform and has a total of 31 million active monthly users.

In this platform thousands of users can create personal pages and communicate with each other by sharing，commenting，and reposting messages.Along with the growth of friendship，there has been a variety of community structures.Jiang et al.studied the Renren social graph structure，and found it similar to the prior studies of Facebook’s social graph［14］.

Some kinds of activities are very popular in the Renren community，such as renewing the mood(literally updating personal state)，blogging，voting and sharing others’blogs.Leaving a message or commenting any of a photo，blog，state，etc.is quite commonly seen.Here，we focus on the activities of users renewing the mood(it refers to the condition they are in or what they are like at a particular time).If a user updates the state，his friends will comment on state.Then the user will reply the comments，and so forth.

In this paper，the dataset contains 76375 samples.Because Renren network is the real name system，most of the 76375 users are acquaintances in off-line.In more than two years，76375 users posted 631252 states and triggered 920584 comments.For each state，the timestamp，sender and the list of replier(but not the content)were recorded.Each user as a node，if one pair of users has comment interactions，we produce a link between the two nodes.For each user i，we use sidenotes the strength of comment and kidenotes node degree.

The results of data processing are shown in Figs.1 to 3.With further analysis of the 272 students of BUPT(Beijing University of Posts and Telecommunications)，it is found that each user has an average of 280 friends.The number of users’friends is heterogeneous.Some user’s friend number is over one thousand;however，some users only have a few dozen.In addition，only 13.4% of the friends would often access the user’s home page and comment on states.It can be seen from Fig.4，the circles is the nodes degree k(it means that the number of friends who comment the user’s states during the observation time window)，and the squares is the number of friends for each user.Nodes degree k to the number of friends is exponential growth with the exponent 1.5.

Fig.1 Distribution of degree

Fig.2 Distribution of strength

Fig.3 Correlation of nodes degree and nodes strength

Furthermore，we study the activity patterns of Renren users.We record the time intervals of users logging in their Renren homepage.It is found that，at the population level，the user active time interval follows power-law distribution(as shown in Fig.5).The result suggests that user activity patterns are heterogeneous.

Fig.4 Relationship between nodes degree and number of friends

Fig.5 Distribution of user active time interval

3 Model

We propose a SI(Susceptible-Infected)propagation model based on community structure to simulate the information propagation in online social networks.In the model，we consider a network with N nodes and G groups，where G≪N.Each group is thus a sub-network of nodes n=，which can be either scale-free，small-world，or random.All groups are placed on a two-dimensional square lattice.For each pair of adjacent groups，one node is chosen randomly from each group and a link is added between the two nodes.At this stage all groups are connected through a next-neighbor type of links.In addition，links among groups are generated by randomly selecting pairs of groups distance x in the square lattice according to the probability P(x)～e－γxand linking them，whereγis a control parameter.

In the spread process，initially all individuals are susceptible except for a single infected individual.And the node does not infect his neighbors at each time step.The time interval between two consequent active steps of an infected individual follows a power-law distribution P(τ)～τ－α.Each message may attract the individual’s attention with probabilityλ，namely，the individual will forward the message with probabilityλ.

4 Simulation Results

For a piece of information to spread on a group network，the number of links among the groups determines the range and velocity of information propagation.If the average degree＜k＞fixed，the minimally required average number of group linkscan be estimated［15］.Here，we analyze the relationship between the fraction of infected nodes I and the average number of links among the groups LM，as shown in Fig.6.In Fig.6，there are three curves corresponding to a sub-network of random(circles)，small-world(squares)，and scale-free(triangles).The main parameters are network size N=1×104and the number of groups G=50，other parameters areγ=0，α=2.5，＜k＞=10 andλ=0.5.Inset:the curves are in the semi-log scale.Each data point is the average over 2×103independent runs.

Fig.6 Fraction of infected node I as the function of Lm

In order to investigate the impact of human groups on the range of information spread，we let the number of groups vary from 50 to 500.And we fix other parameters，such as network size N=1×104，Lm=10，γ=0，α=2.5，＜k＞=10 andλ=0.5.From the simulation results，it is seen that that as G varies from 50 to 500，the fraction of infected nodes I remains approximately constant(between 0.7 and 0.8)(as shown in Fig.7).The mean infected time Tm，however，as shown in Fig.8，is apparently nonmonotonic and exhibits a bell-shape behavior.Three curves correspond to a sub-network of random(circles)，small-world(squares)，and scale-free(triangles).Each data point is the average over 2×103independent runs.

Fig.7 Fraction of infected nodes I as the function of the number of groups G

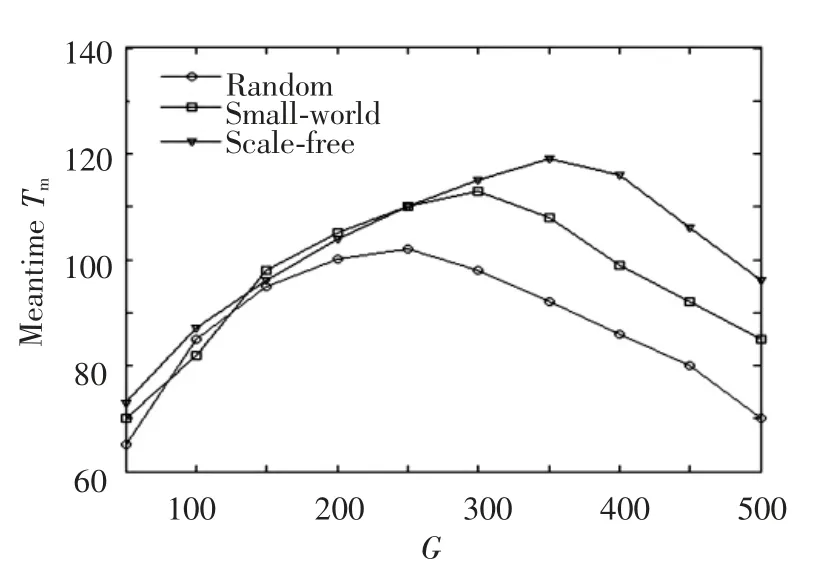
Fig.8 Mean infected time T m as the function of the number of groups G

5 Theoretical Exp lanation

In order to analyze the above results，we seek a theoretical explanation.We establish the SI model based on community structure and consider the spread of information from a seed node on a two-dimensional square lattice.According to the assumptions of the SI dynamics，once a node is infected，it cannot be infected again.It is assumed that a node i at the point r=(x，y)is infected at time t－τfrom the node j at r=(x，y－a)，whereτand a are the time step and lattice constant，respectively.At time t，this newly infected node infects one of its nearest-neighbor nodes，if it is susceptible.If all nearest-neighbor nodes of the newly infected nodes are susceptible except for the node at r=(x，y－a)，the probability for any of these susceptible nodes to be infected at time t+τis 1/3(as shown in Fig.9).

Let P(r，t)be the probability that a node at the point is infected at time r=(x，y).We have

Subtracting P(r，t+τ)from both sides and dividing byτ，we get，

Fig.9 Schematic diagram of propagation process

In the continuum limit a→0，τ→0，Eq.(1)is transferred to，

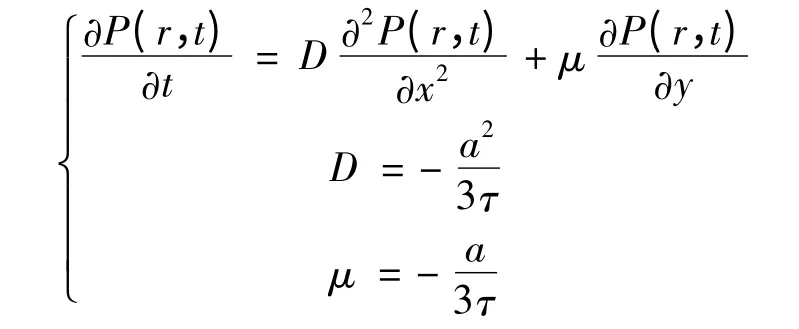
Since|D|≪|μ|，the diffusion term can be neglected，we get

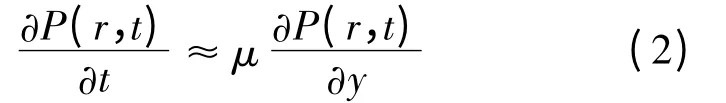
In Eq.(2)，the term on the right-hand side is derived by taking into account the fact that only the unidirectional spreading can also occur in the direction，so the equation governing the propagation of infection in the two-dimensional lattice is，

where v is a constant.For a complex network，although we are not able to derive a similar equation，the basic dynamical process for infection spreading is the same.

6 Discussion

With the popularity of Web 2.0 concept and the fast development of related technologies，the online Social Networking Service as a form of network application has developed rapidly.Nowadays，the online network has become an important platform to disseminate information，express views and interact with each other.Different from the traditional ways of information dissemination，online social network makes the spread of topics and opinions rapid，and increases the probability of sudden events happening.Therefore，the formation and evolution of opinions are becoming more complex and uncertain，and traditional mathematical model of spreading dynamics can not depict the phenomenon of information spreading and opinion evolution in online social network.In this paper，we proposed a SI(Susceptible-Infected)model based on community structure.In the model，the heterogeneity of users’active time was taken account.For a piece of information propagation in online social networks，we would expect the range and velocity of spread to increase with the number of groups G.We found，however，that the fraction of infected nodes I remains approximately constant and the mean infected time Tmcan be maximized for a specific value of G.And we also found that the number of links among communities determines the fraction of infected nodes:with the increases of the average number of links among communities，the fraction of infected nodes increases rapidly.

The results will be of great significance:the information will last relatively short for group networks which have either a small or a large number of groups.In the case of rumor propagated in an online community，assuming that the size of an online community is proportional to the number of groups in the underlying online social network，the rumor may last long not for communities of small or large size，but for those of medium size.The results can be useful for optimizing or controlling information，such as propagating rumors in online social networks.

［1］Li Z，Guan X H，Yuan R X.Modeling collective blogging dynamics of popular incidental topics.Knowledge and Information System，2012，31:371－387.

［2］Cha M，Mislove A，Gummadi K P.A measurement-driven analysis of information propagation in the Flickr social network.Proceedings of the 18thInternational Conference on World Wide Web.New York:ACM，2009.721－730.

［3］Yang J，Leskovec J.Modeling information diffusion in implicit networks.Proceedings of the 2010 IEEE International Conference on Data Mining.Washington DC:IEEE Computer Society，2010.599－608.

［4］Zhao J C，Wu J J，Xu F，et al.Information propagation inonline social networks:a tie-strength perspective.Knowledge and Information System，2012，32:589－608.

［5］Karsai M，Kivela M，Pan R K，et al.Small but slow world:how network topology and burstiness slow down spreading.Physical Review E，2011，83:1－4.

［6］Onnela J P，Saramaki J，Hyvonen J，et al.Structure and tie strengths in mobile communication networks.Proceedings of the National Academy of Science of the United of America(PNAS)，2007，104(18):7332－7336.

［7］Wu L R，Yan Q.Modeling dynamic evolution of online friendship network.Communications in Theoretical Physics，2012，58(4):599－603.

［8］Watts D J，Dodds P S，Newman M E J.Identity and search in social networks.Science，2002，296(5571):1302－1305.

［9］Palla G，Derenyi I，Farkas I，et al.Uncovering the overlapping community structure of complex networks in nature and society.Nature，2005，435:814－818.

［10］Wu X Y，Liu Z H.How community structure influences epidemic spread in social networks.Physica A:Statistical Mechanics and its Applications，2008，387(2－3):623－630.

［11］Liu Z H，Hu B.Epidemic spreading in community networks.Europhys.Lett.，2005，72(2):315－321.

［12］Wei H，Li C G.Epidemic spreading in scale-free networks with community structure.Journal of Statistical Mechanics:Theory and Experiment，2007，1:14－20.

［13］Tang S J，Yuan J，Mao X F，et al.Relationship classification in large scale online social networks and its impact on information propagation.Proceedings of INFOCOM.Washington DC:IEEE Computer Society，2011.2291－2299.

［14］Jiang J，Wilson C，Wang X，et al.Understanding latent interactions in online social networks.Proceedings of the 10thACM SIGCOMM Conference on Internet Measurement.New York:ACM，2010.369－382.

［15］Huang L，Park K，Lai Y C.Information propagation on modular networks.Physical Review E，2006，73:1－4.