齿轮箱减振降噪优化设计方法研究

李宏坤，郭 骋，房世利，丁 健

(1.大连理工大学 机械工程学院，大连 116024;2.大连理工大学 工业装备结构分析国家重点实验室，大连 116024;3.沈阳鼓风机集团公司，沈阳 110869)

齿轮传动是应用最为广泛的机械传动方式，其被广泛应用于机械电子、采矿冶金、汽车交通、航空航天等领域。随着现代工业化程度的不断提高，包括齿轮箱在内的机械设备的振动与噪声问题正在越来越受到重视。齿轮箱振动、噪声的主要来源为轮齿之间啮合时的相互作用，相关研究表明齿轮箱是以结构噪声为主的设备，对振动、噪声传递路径进行分析可知，其主要分为3种途径:一是齿轮对啮合过程产生的啮合声以固体声的形式经齿轮、轴和轴承等传递至箱体，通过箱体各壁面振动辐射到齿轮箱外部空间中，形成所谓第一次空气声;二是齿轮对啮合过程产生的啮合声直接辐射到齿轮箱内部空间中，再传递至箱体各壁面使其振动向箱外空间辐射噪声，形成所谓第二次空气声;三是啮合声通过齿轮箱存在的各种缝隙向外辐射。研究表明齿轮箱约90%～95%的辐射声能量是通过第一种途径［1］。因此，齿轮箱箱体的优化设计是整个齿轮箱减振、降噪优化设计的重要研究内容。

国内外学者在齿轮箱减振、降噪优化设计方面已经开展了广泛的研究工作［2－7］，但是研究的越深入就会遇到更多更难的问题，至今为止很多的研究工作仍然处在理论与试验研究、振动噪声数值仿真方法研究等阶段，在此基础上探究齿轮箱的振动与辐射噪声特性，并寻找薄弱环节，进行相应的结构改进工作。针对较普遍存在的振动与噪声不同步优化考虑、结构改进存在的盲目性等问题，本文采用振速法原理、有限元求解、贡献量分析等方法，在兼顾齿轮箱箱体振动和噪声特性的基础上，采用优化求解器对其进行优化求解与改进设计。

1 理论基础

研究表明，齿轮箱类主要辐射结构噪声的设备，其结构表面振动速度与辐射噪声之间存在着一定的比例关系，但是以降噪为目标的结构改进时常出现表面振动速度降低，但降噪效果却不明显的现象，这说明了这一类结构其辐射噪声的特性受到声辐射面积、表面振速、声辐射效率等多种振动、声学因素的影响［8］。本文为了实现在箱体优化求解过程中能够兼顾振动、噪声两个特性，分别利用贡献量分析、振速法原理等对箱体的特性进行分析，并制定了能够表征箱体振动、噪声量的优化目标函数。

1.1 模态贡献量分析

结构模态贡献量分析能够计算结构在确定的载荷激励下各阶模态对于不同位置响应的贡献量大小，其不仅与结构本身的固有特性有关，还与结构所受到的载荷以及响应的位置有关。

由于一个结构系统的振动微分方程经过模态变换之后可得到用模态参数表示的非耦合振动微分方程为:

式中:yj为模态坐标;ωj为第j阶模态固有圆频率;ξj为模态阻尼;fj为模态坐标中的载荷。

对于一个稳态的正弦激励而言，fj具有如下的形式:

其中:fjc为复数力幅值;Ω为施加的圆频率;

假如式(1)在任何时刻都成立，则需要yj具有如下形式:

其中:yjc为第j阶模态坐标值的复幅值;

将式(3)微分，并将其与式(2)代入式(1)得到:

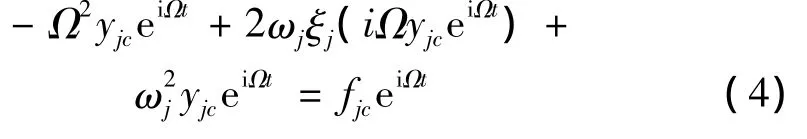
整理得:

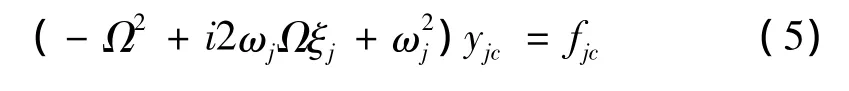
则:

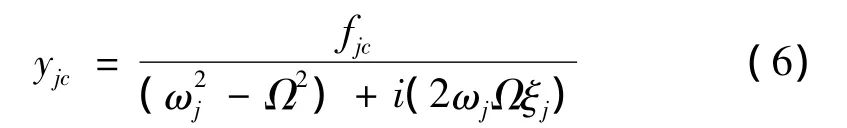
来自各阶模态的贡献量则可以表示为:

其中，{Cj}为第j阶模态的贡献量;{φj}第j阶模态振型向量。

最终，复位移可以通过下式获得:

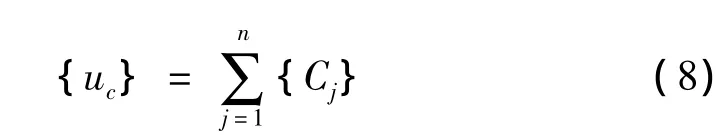
1.2 振速法原理

振速法实际上是在研究振动与声之间关系的基础上提出的方法，结构声辐射引起的空气声功率级可按如下公式计算［9］:

本文利用ANSYS软件的动力学模块对齿轮箱进行稳态动力学计算求解，提取齿轮箱箱体非支撑面外表面各节点的振动速度求解振动速度级均值LV'i，那么速度级均值则可通过下式来获得:

式中:L'Vi为未修正的实际振动速度级;KIi、Kmi为修正因数(一般情况下可忽略);

根据式(9)也可以发现，如果振动结构的辐射效率σ已知，那么可通过计算结构表面振速的均方值来获得其所辐射的声功率级。为此本文将应用高效的声学求解软件LMS Virtual.Lab Acoustics对齿轮箱箱体辐射效率σ进行求解。

1.3 ANSYS优化求解原理

采用ANSYS软件的优化求解器进行箱体的优化求解计算，在ANSYS软件中提供了两种优化求解方法分别是零阶方法和一阶方法。零阶方法能够满足大多数工程问题的求解需要，是一个较为完善的处理方法。一阶方法适合于对求解精度有更高要求的场合，其利用偏倒数求解基于目标函数对设计变量的敏感程度。本文采用一阶方法来进行齿轮箱箱体的优化求解［10］。一阶方法首先需要将约束问题通过引入罚函数的方式转换为非约束问题，以此来提高问题求解的效率，接着将目标函数与状态变量罚函数求偏导数以确定在设计空间中的搜索方向。在迭代过程中使用最速下降法或者共轭梯度法直到求解结束。下面对一阶方法原理进行简要的概述。首先通过下式将约束问题转化为非约束问题:

其中:Q 无量纲，为非约束的目标函数;Px，Pg，Ph，Pw为施加于约束的设计和状态变量的罚函数;f0为从当前的设计集中选取的参考目标函数值;约束的满意度是通过响应面参数(response surface parameter)即q这个参数来控制的。对设计变量施加外部罚函数(Exterior penalty functions)Px。状态变量约束使用扩展内部罚函数(extended-interior penalty functions)Pg，Ph，Pw。

2 齿轮箱贡献量分析

2.1 齿轮箱稳态振动响应分析

本文采用Solidworks软件完成了整个齿轮箱的建模工作，将齿轮啮合模型导入ADAMS软件并进行相关设置完成齿轮对刚性体动力学建模。根据实际工况，主要设置为在四个轴承位置定义转动副;在主动轴输入端添加驱动，转速设置为1 500 r/min;在从动轴输出端定义负载扭矩为2 N/m;在两齿轮之间定义接触力。仿真计算之后能够对各轴承中心位置所承受的载荷变化曲线进行提取，图1为输出轴负载端轴承位置水平方向受力频谱图。

齿轮箱为两圆柱直齿齿轮单级传动方式，输入小齿轮和输出大齿轮的齿数分别为55和75，结合上图可知，轴承所承受的激励力主要频率成分为1 375 Hz及其倍频，1 375 Hz为1 500 r/min转速下齿轮箱的啮合频率。

图1 输出轴负载端轴承位置水平方向受力频谱图Fig.1 Frequency domain curve of the output shaft at the load end in the horizontal direction

本文利用ANSYS软件的APDL参数化设计语言完成齿轮箱箱体的建模、加载、求解和后处理等工作。为了提高求解的效率和精度，研究中采用solid187单元对箱体进行网格划分，总共划分了95 771个单元，116 714个节点，箱体三维模型如下图2所示。

图2 齿轮箱箱体三维模型与有限元模型Fig.2 The model of gearbox housing

另外，轴承是较难处理的环节，为了适当简化系统，在箱体4个轴承所在位置的中心建立mass21质量单元，并将之与轴承座相应位置节点通过combin14弹簧阻尼单元进行连接来模拟轴承，并对mass21单元分配相应的质量属性。

采用建立的有限元模型进行模态仿真计算，与模态试验结果进行对比，验证有限元模型的可靠性。提取ADAMS计算得到的轴承中心位置的载荷谱，利用APDL编写程序将其读入 ANSYS中并加载至相应mass21单元位置。完成相关设置之后即可进行箱体稳态振动响应求解。

2.2 齿轮箱模态贡献量分析

根据模态贡献量原理可知，结构振动时其主要贡献模态与结构的振动响应频率有关，从ADAMS和ANSYS稳态振动响应求解结果可知，齿轮箱主要的振动响应频率为1 375 Hz，另外，实际测试结果也表明，箱体各壁面的振动以法向为主，因此，本文选取箱体各壁面具有代表性典型节点，对模态贡献量进行整理与分析。使用箱体模态叠加法对齿轮箱箱体进行谐响应计算，计算完成之后即可对各阶模态贡献量进行输出。由于在ANSYS软件中，软件最后对模型所有节点的信息进行了输出，软件也没有对该文件提供相应的后处理功能，因此，使用LabView软件编制了提取程序，实现了对包含贡献量数据的结果文件的提取。典型节点位置如图3所示。由于篇幅所限，本文中只给出了1 375 Hz频率成分振动响应模态贡献量分析结果。

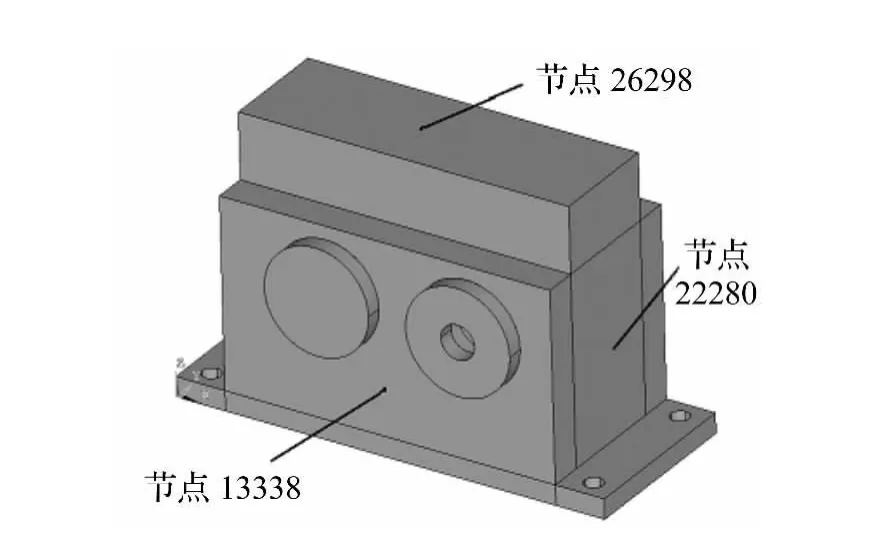
图3 齿轮箱箱体典型节点位置Fig.3 The typical node position of the gearbox

图4 频率1 375 Hz下模态贡献量Fig.4 The modal contribution coefficient at 1 375 Hz

从图4可知，在1 375 Hz振动响应下三个节点位置均以第三阶模态贡献量最大，由于1 375 Hz频率成分的振动响应幅度远大于其余频率成分，因此，可以判定齿轮箱在1 500 r/min转速条件下，箱体振动响应主要贡献模态为第三阶，该阶模态也是下文优化设计的主要目标之一。

2.3 齿轮箱声学面板贡献量分析

采用LMS Virtual.Lab Acoustics声学仿真计算软件对齿轮箱进行声学面板贡献量分析，以确定声学主要贡献面板。首先，本文根据齿轮箱箱体本身的形状特点进行了边界元网格和面板区域的划分，如图5所示。

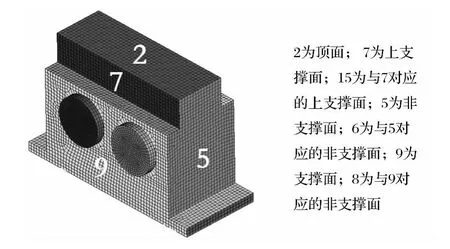
图5 齿轮箱箱体边界元网格和面板区域划分Fig.5 Boundary element mesh and panel division of the gearbox housing

本文共划分了如图5所示的21个面板区域，并建立ISO3744－1994场点网格，最后插入ATV响应计算模块，在此基础上对声学面板贡献量进行分析。本文对面板声功率贡献量进行了求解，计算结果如图6所示。

图6 1 375 Hz面板声功率级贡献量Fig.6 Panel acoustic power level contributions at 1 375 Hz

从图中我们可以发现，5、6号非支撑面声功率级最大，两者的辐射声功率级分别达到了70.32和72.05 dB，箱体总的辐射声功率级为74.74 dB。

2.4 振速法齿轮箱箱体声功率级求解

根据1.2中论述的振速法的相关原理与公式，在箱体稳态振动响应求解的基础上，使用APDL语言编写相应的程序，求解箱体面板的辐射声功率级。考虑到求解的复杂性，为了尽量减少误差的引入，同时也不失去计算的意义，本文对齿轮箱箱体非支撑面的辐射声功率级进行求解。

主要利用式(9)对非支撑面的辐射声功率级进行求解，需要注意的是式中参数σ称之为辐射效率，该参数表征了结构辐射噪声的能力，它除了与结构固有的结构性能有关之外，还与结构所承受的激励力特性以及结构所在的声环境有关。本文采用LMS Virtual.Lab Acoustics对齿轮箱箱体辐射指数进行求解。

图7 齿轮箱非支撑面辐射效率Fig.7 The radiation efficiency of the gearbox unsupported surfaces

图7为计算得到的齿轮箱非支撑面的辐射效率对数曲线，从图中可以发现辐射效率σ随着频率的增加而增加，当达到第一个峰值之后，其幅值有所下降，接着又逐渐增加直到逐渐在1附近上下波动。随着频率的增加，声波波长变短，振动模态不同相位部分声辐射之间的相互影响越小，因此，频率越高，声辐射效率越高。一般认为，在临界频率以上辐射效率σ≈1。临界频率是指结构表面弯曲波波长和空气中声波波长相等时的振动频率。对于图7中曲线出现的一些异常波动，幅值甚至超过了1，主要是由于结构边界元模型一些结构特征之间的相互影响造成的，可以忽略。

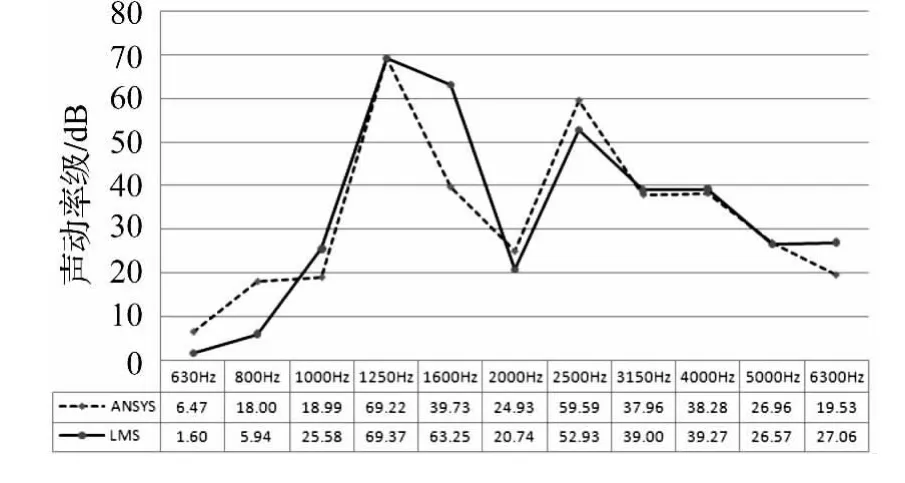
图8 齿轮箱5号非支撑面辐射声功率级对比Fig.8 The comparison of acoustic power level radiated from panel 5

由于ANSYS稳态振动响应直接计算得到的为各节点的位移，所以，在0～6 000 Hz频带范围内，以125 Hz为频率间隔，对两非支撑面所有节点的位移值进行微分，总共计算48处频率下的速度有效值，继而求解非支撑面上的速度级均值，对计算得到的辐射效率曲线相应频率下的值进行提取，引入非支撑面的辐射面积为0.033 52 m2完成相关参数设定。最终即可实现在有限元计算后处理中完成齿轮箱非支撑面辐射声功率级的求解。

图8为利用LMS软件和有限元振速法计算得到的5号非支撑面辐射声功率级的对比，由图可知，频率范围在630 Hz至6 300 Hz内，利用振速法和LMS软件的声功率结果趋势相近，特别是在主要频率为1 375 Hz，即以1 250 Hz为中心频率的频带范围内，两种计算方法的结果相差很小。两者计算结果较为一致，验证了有限元振速法的可靠性。

3 齿轮箱优化设计

前文采用ANSYS软件对齿轮箱箱体的稳态振动响应进行了求解，在此基础上结合振速法与辐射效率的求解，在有限元计算后处理中实现了箱体非支撑面辐射声功率及的求解。从声学面板贡献量分析结果可知，箱体非支撑面的辐射声功率及要远大于其余面板，因此，其辐射噪声数值能够代表整个箱体的噪声辐射水平。

整个优化求解过程需使用APDL语言完成，包括:建模、网格划分、模态计算、加载、振动响应求解、后处理(非支撑面声功率级求解)、优化设计变量、设置优化参数，然后就可利用ANSYS软件的优化求解器进行循环优化求解，最后得到优化计算结果。

从模态贡献量结果可知，第三阶模态为箱体振动的主要贡献模态。因此，本文齿轮箱箱体减振降噪优化设计的目标函数有两个，分别为非支撑面的辐射声功率级降低和第三阶模态的固有频率的提高。

通过设定合理的变量区间，对计算结果能够起到积极的影响。采用一阶方法，迭代20次，优化求解之后，得到了一组最优的壁面厚度组合。利用该组壁厚尺寸对齿轮箱箱体重新进行建模、加载、有限元和声学仿真计算，验证降噪效果。此处仅列举了5号非支撑面优化前后辐射声功率级三分之一倍频程对比图，如图9所示。

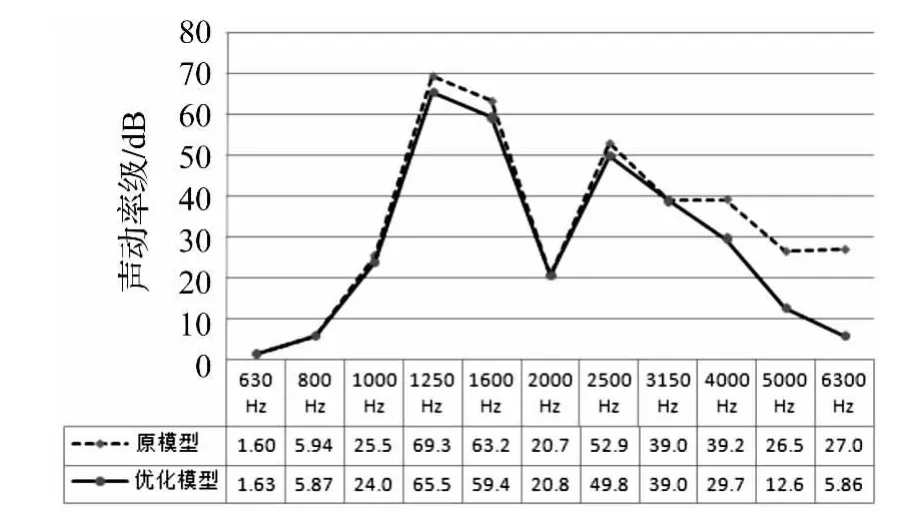
图9 5号非支撑面辐射声功率级优化前后对比Fig.9 The chart of the comparison of the radiated acoustic power level of the panel 5

从表1可知，两非支撑面的辐射声功率级降幅分别达到了3.84 dB和6.61 dB，与此同时，整个齿轮箱箱体辐射声功率级也下降了5.32dB。这说明对齿轮箱箱体的主要噪声源进行噪声控制能够同时对齿轮箱整体的辐射噪声进行较好控制;采用本文的齿轮箱箱体的减振、降噪优化设计方法能够取得较好的优化效果。

表1 优化前后声功率级对比Tab.1 The comparison of the acoustic power level before and after the optimization

4 结论

(1)对某齿轮箱箱体的结构模态贡献量进行了分析，识别出第三阶模态为主要贡献模态。对齿轮箱箱体进行了声学面板贡献量分析，确定了其主要噪声辐射源为两非支撑面。

(2)结合振速法原理，在齿轮箱箱体有限元振动响应计算的基础上，实现了其非支撑面辐射声功率级的求解，该参数能够较好的表征整个箱体的振动、噪声情况。

(3)采用ANSYS软件的优化求解器，实现了齿轮箱箱体的减振、降噪优化求解，得到了箱体最优壁面厚度组合。本文的相关研究对齿轮箱的振动、噪声控制提供了借鉴意义。

［1］徐志锋，邵忍平.齿轮系统噪声预估及声诊断方法研究［J］.计算机测量与控制，2009，17(9):1688 －1691.XU Zhi-feng，SHAO Ren－ping.Forecast of sound pressure level of gear systems and fault diagnosis based on acoustics［J］.Computer Measurement＆ Control，2009，17(9):1688－1691.

［2］薛延华，吴新跃.一种齿轮箱振动控制方法［J］.海军工程大学学报，2001，13(1):99 －103.XUE Yan-hua，WU Xin-yue.A method of controlling gearbox vibration ［J］.Journal of naval university of engineering，2001，13(1):99－103.

［3］Eiichirou－TANAKA.Vibration and sound-radiation analysis for designing a low-noise gearbox with a multi-stage helical gear system［J］.Mechanical Systems Machine Elements And Manufacturing，2003，46(3):1178－1185.

［4］Guan Y H.Experimental study on active vibration control of a gearbox system［J］.Journal of sound And Vibration，2005，282:713－733.

［5］张 雷.船用齿轮箱的灵敏度研究及结构优化［D］.哈尔滨:哈尔滨工程大学，2010.

［6］焦映厚，孔 霞，蔡云龙，等.基于FEM和BEM法的大型立式齿轮箱振动噪声计算及测试分析［J］.振动与冲击，2012，31(4):123 －127.JIAO Ying-hou，KONG Xia，CAI Yun-long，et al.Vibration noise calculation and testing analysisoflarge vertical planetary transmission gearbox based on FEM and BEM［J］.Journal of Vibration and Shock，2012，31(4):123 －127.

［7］周建星，刘 更，马尚君.内激励作用下齿轮箱动态响应与振动噪声分析［J］.振动与冲击，2011，30(6):234 －238.ZHOU Jian-xing，LIU Geng，MA Shang-jun.Vibration and noise analysis of gear transmission system［J］.Journal of Vibration and Shock，2011，30(6):234 －238.

［8］李 民，舒歌群，梁兴雨.4100QB柴油机齿轮室盖声辐射效率试验研究［J］.农业工程学报，2010，26(12):148－152.LI Min， SHU Ge-qun， LIANG Xing-yu. Experimental research on radiation efficiency of the gear-cover of 4100QB diesel engine［J］.Transactions of the CSAE，2010，26(12):148－152.

［9］GB/T 16539－1996声学 振速法测定噪声源声功率级 用于封闭机器的测量:［S］.

［10］张朝晖.ANSYS11.0结构分析工程应用实例解析［M］.北京:机械工业出版社，2008.