弹性接触层对双层柱壳中纵波传播特性的影响

高康华，王明洋，宋春明

(解放军理工大学 国防工程学院，南京 210007)

双层圆形柱壳是常用的工程结构之一，如工业中含防护层的输运管道、城市地铁和水底隧道等。此类结构往往轴向长度较大，径向材料差异、壳体厚度以及层间接触方式等均会影响结构的振动特性，为此可通过研究结构中弹性波传播特性分析其动力响应，重点主要在于波频散关系的确定和波结构分析两个方面，当前国内外学者对多层介质中弹性波传播作了大量研究，通常方法是根据边界和层间接触条件构建波频散特征方程，数值求解后得到频散曲线，进而确定各阶模态相应的位移和应力的波结构。如Lowe［1］详细介绍了构建频散方程的传递矩阵法和全局矩阵法，并给出求解复杂频散方程的数值解法;Ryden等［2－4］在此基础上分别推导了多层板和多层柱壳中纵波传播频散方程，研究了三层道路结构和覆盖粘弹性材料层的弹性中空柱壳结构中导波的传播特性，但主要针对的是层间固结接触条件［5］，即内外壳体接触面上应力位移均保持连续。对于层间光滑接触［6］，即接触面法向应力、位移连续，切向应力为零，Valle等［7］研究了该条件下中空柱壳内部包裹实心圆杆结构的周向导波;张慧玲等［8］对层间光滑接触时双层复合筒结构中周向导波的传播进行了理论和数值研究，二者均采用了二维线弹性平面应变理论，未考虑波的轴向传播。对于层状介质中较复杂的层间接触，Rokhlin等［9］采用薄粘弹性层分隔两个不同固体半无限空间的力学模型，分析了粘弹性接触面层对波传播特性的影响;张慧玲等［10］在该模型基础上建立了层筒结构的层间界面模型，进而研究层间界面特性对周向导波的影响。此外，他得安等［11］对超声纵向导波在复合管状结构中传播特性进行分析，侯秀慧等［12］研究了正交各向异性夹层圆柱壳中轴对称自由简谐波的传播问题，得到各种夹层结构波传播的频散关系。

本文将在上述文献基础上，针对具有较薄弹性接触层的双层中空柱壳结构提出确定频散关系的简化方法，并分析接触层特性对轴对称纵向导波频散关系及壳体内应力和位移的影响，为此类结构动力响应分析提供理论参考。

图1 具有薄弹性接触层的双层柱壳模型简图Fig.1 Calculation diagram of double layered cylinder with a thin elastic contact layer

1 基本理论

图1给出了具有较薄弹性接触层的双层中空柱壳结构模型，材料均视为各向同性弹性介质，此类结构实际上是层间固结接触的三层柱壳，但当接触层厚度h0远远小于波长λ0时，可忽略接触层介质惯性运动，引入弹性层接触界面条件简化频散方程。图中a为柱壳内半径，d为外半径，b为中心距外壳内壁距离，h0、h1、h2分别为接触层、内壳和外壳的厚度。

忽略体力，柱坐标系(r，θ，x)下 Navier运动方程为:

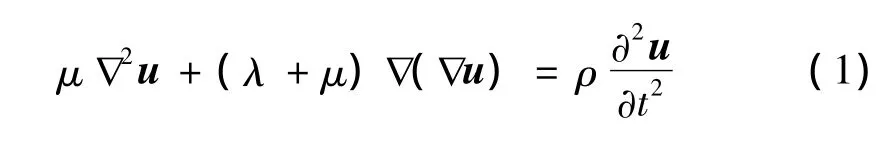
式中:u 为关于 ur，uθ，ux的柱壳位移矢量，ur，uθ，ux为r，θ，x方向上的位移;ρ为材料密度;λ，μ为拉梅常数;t为时间变量;∇和∇2分别为那勃勒算子和拉普拉斯算子。

利用Helmholtz定理有:式中:φ 为位移场标量势函数，ψ 为关于 ψr，ψθ，ψx的位移场矢量势函数，ψr，ψθ，ψx为 r，θ，x 方向上分量。

为方便计算，引入标量势函数χ，Φ，使得:

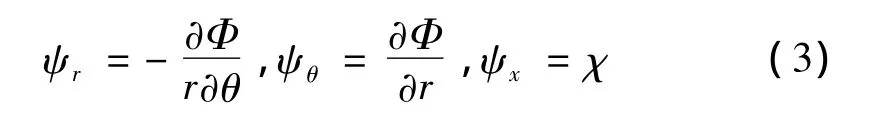
将式(2)、(3)代人式(1)可得:

式中:cp=，分别为膨胀波速和等容波速。

轴对称条件下 uθ≡0，∂/∂θ≡0，壳体位移及应力可视为仅关于势函数φ、Φ的函数，有:

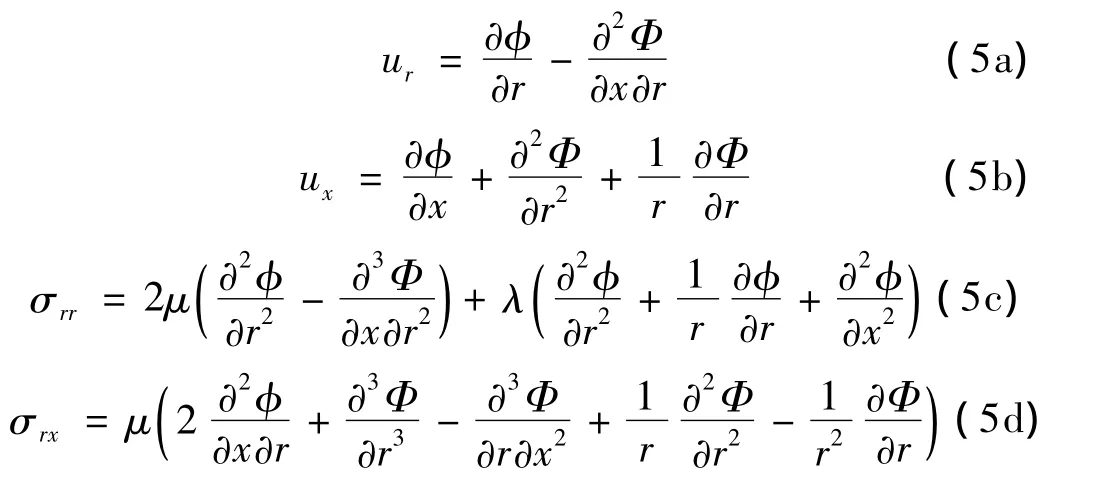
式中:σrr为径向应力，σrx为轴向应力。

轴对称条件下，式(4)前两项可化为:

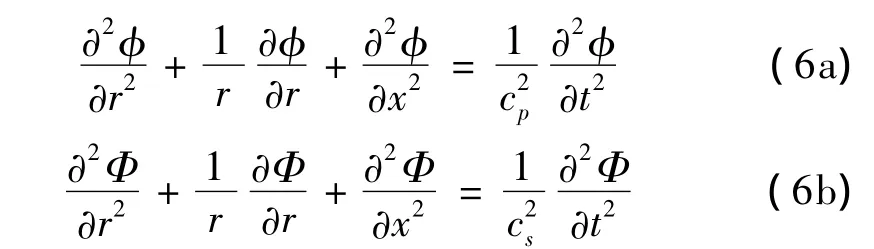
假设纵波沿x正向传播，方程组(6)解设为:

式中:k为波数，角频率ω=kcf，cf为相速度，i表示虚部单位。

将式(7)代入式(6)可得到 φ0(k，r)、Φ0(k，r)的关于贝塞耳函数表达式，具体可按文献［13］选取，在此主要考虑第一模态中cf＜min(cs，cp)的情况，故选用虚宗量贝塞尔函数，并对相关参数无量纲化，令Mp=cf/cp，

式中:A，B，C，D 为系数;I0，K0为零阶第一类和第二类虚宗量贝塞尔函数。

将式(8)代入式(5)可得柱壳关于无量纲量r—，的位移、应力表达式如下:

式中:I1，K1为一阶第一类和第二类虚宗量贝塞尔函数。

双层圆形柱壳各内外层壳体位移、应力均可用式(9)确定。为方便研究，令0=h0/λ0，xs=h1/h2，xs1=h0/h2，γ1= μ0/μ21=h1/d2=h2/d=cs/cp，则 ε1=1－(1+xs+xs1)2，ε2=1 －2。计算时各层无量纲波速有以下关系:

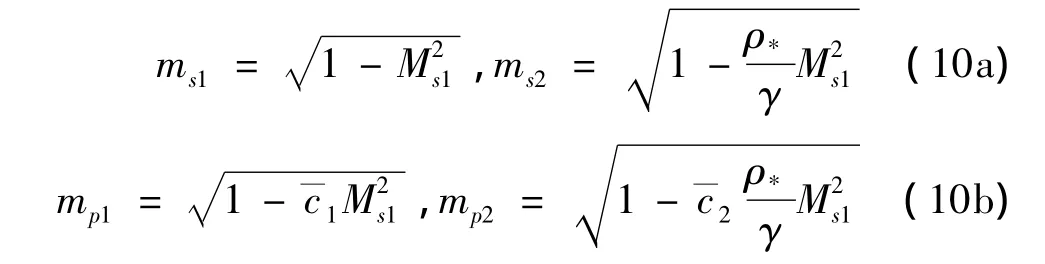
式中:γ = μ2/μ1，ρ*;下标1、2表示柱壳内、外层。

系数 Ai，Bi，Ci，Di(i=1，2)可根据层间接触条件及边界条件确定。对具有弹性接触层的双层柱壳，在内外自由边界条件下有:

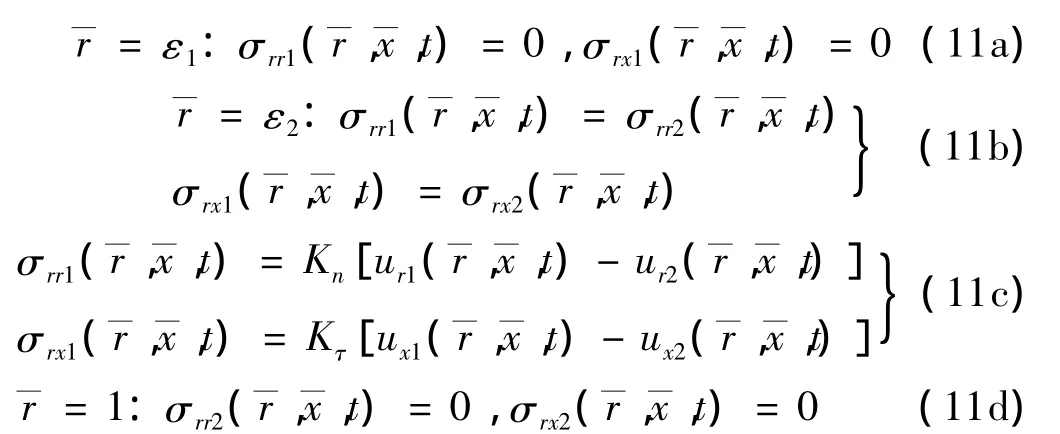
式(11c)即为忽略接触层惯性运动后引入的弹性层接触界面条件，其中 Kn=E0/h0，Kτ= μ0/h0，E0、μ0为夹层的弹性模量和剪切模量，Kn、Kτ为夹层单位层厚的法向和切向刚度。当Kn→∞和Kτ→∞时，式(11c)即转化为固结连接边界条件［10］:

将式(9)代入式(11)中可得到双层柱壳关于参数Ai，Bi，Ci，Di(i=1，2)的线性齐次方程组，写成矩阵形式如下:

式中:X=［A1，B1，C1，D1，A2，B2，C2，D2］，A 为系数矩阵，其中的元素aij(i=1…8;j=1…8)见附录。

式(12)有非零解的条件是矩阵A行列式等于0，即:

式(13)即为轴对称纵波在具有较薄弹性接触层的双层柱壳中传播的频散方程，可将其视为关于无量纲波数η和相速度Ms1的超越方程，此类方程求解方法很多［1，13－14］，常用方法是先固定未知参数 η 或 Ms1的值，再在确定的范围内按一定步长对Ms1或η进行逐步搜根，从而得到方程的数值解，并绘制出相应的频散曲线。由于此处不涉及到波的衰减和泄漏，可采用二分法求解这一实频散方程，即满足计算稳定性又可避免方程根的遗漏［1］。根据得到的频散曲线，可将给定波数 η 相应的(η，Ms1)代入式(12)，求得系数 Ai，Bi，Ci，Di(i=1，2)，并根据式(9)计算壳体内位移和应力。

2 算例分析

文献［13］给出了单层镍铬铁合金管的轴对称纵向导波相速度频散曲线，计算参数为:a=8.23 mm，d=9.45 mm，壁厚 d'=1.22 mm，ρ=8.4 g/cm3，cp=6.29 km/s，cs=3.23 km/s。用本文方法计算时可认为内外层壳体和接触层材料一致，计算参数取为:ρ1=ρ2=8.4 g/cm3，h1=0.8 mm，h2=0.32 mm，h0=0.1 mm，cp1=cp2=6.29 km/s，cs1=cs2=3.23 km/s。图 2 为本文方法计算结果与文献中曲线的对比图，图中f为频率。

图2 单层镍铬铁合金管的相速度频散曲线Fig 2 Phase velocity dispersion curves of a single layer nickel-chromium alloy pipe

图2中显示本文方法的计算结果与文献［13］中计算曲线较为吻合，表明h0≪λ0时本文方法的正确性。应当注意的是，弹性波是扰动借助连续介质中各质点惯性运动形成的附加弹性力而逐渐传播的过程，本文忽略接触层介质惯性运动而引入弹性层界面接触条件，实际上是忽略了接触层介质的动力响应，这在h0≪λ0时是能够满足工程需要的，但在h0增大或波长减小时，会给计算结果带来一定偏差，下面通过算例进行分析。

选取内外层壳体材料为钛，接触层为铜的双层柱壳，计算参数:接触层泊松比 ν0=0.333，γ1=0.874，γ=1，ρ*=1，ρ1= ρ2=4.46 g/cm3，cp1=cp2=6.06 km/s，cs1=cs2=3.23 km/s。用式(9)～式(13)计算纵向 L(0，1)模态相速度频散曲线，并将得到的结果与DISPERSE软件［13］计算生成的频散曲线进行对比，如图3所示。

图3 双层柱壳纵向L(0，1)模态相速度频散曲线Fig 3 Phase velocity dispersion curves of double layered cylinder for longitudinal L(0，1)mode

图3给出了接触层厚度不同时纵向L(0，1)模态相速度频散曲线，其中运用DISPERSE软件计算时，考虑了夹层的惯性运动，将结构视为钛—铜—钛三层弹性中空柱壳结构。图中曲线表明，当波数较大时，波长较短，用本文方法的计算结果与DISPERSE生成的频散曲线有偏差，接触层厚度越小，偏差越小;随着波数的减小，波长增大，两种计算曲线逐渐一致，说明此时忽略接触层惯性运动对频散曲线影响不大。表1列出了不同层厚情况下，两种方法计算得到的相速度相对差值Δcf在较小范围内的h0临界值，计算参数如前所示。

表1 Δcf在较小范围时h0的临界值Tab.1 The maximum value of h0under the smaller range of Δcf

表1中 Δcf= cf1－cf2/cf2，其中 cf1和 cf2分别为在给定波数时用本文方法和DISPERSE软件计算得到相速度值，0l为给定差值范围时0的最大值。表1显示此例中Δcf较小时，h0至少要比波长λ0小两个量级，且相对差值越小，0l也越小，从而验证了本文方法在h0≪λ0时的合理性。

下面通过算例说明接触层特性对双层柱壳结构内纵波传播的影响，主要考虑纵波L(0，1)模态。初始条件为:ν0=0.28，x3=10，xs1=0.1，2=0.004，γ1=0.001，γ =100，ρ*=100，1=2=0.553，ε1=0.9556，ε2=0.995 8。图4给出了弹性层接触和固结接触两种界面条件下双层柱壳纵向L(0，1)模态频散曲线，固结接触时不考虑夹层，按接触界面应力、位移连续采用全局矩阵法［1－4］计算。

图4 弹性层接触与固结接触时L(0，1)模态频散曲线对比Fig 4 Comparisons of L(0，1)mode disperse curves between results calculated under elastic contact layer interface condition and continuous contact interface condition

图4中当η≤15时两种接触界面情况下的频散曲线较为一致，表明波数较小时弹性接触层对频散关系影响不大;随着波数的增大，η＞15时，两种界面条件下的频散曲线逐渐产生差异，且夹层厚度越大差异越大，说明对于短波长而言接触层特性影响不可忽略。此外，图4还表明相同条件下泊松比对纵波L(0，1)模态的频散关系影响不大。

图5给出了波长较短的η=40时具有弹性层接触的双层柱壳内应力、位移分布，并与层间固结接触进行了对比。图中无量纲量，其中上标“0”表示根据初始条件计算所得参数值，下标“max”表示相应参数的最大值。

图5 壳体内应力和位移分布Fig 5.Distribution of stress and displacement along cylinder shell thickness

图5显示双层柱壳含有弹性层接触界面时，径向应力σrr由内壳内壁沿径向增大至接触面处达到峰值，而后逐渐减小，轴向应力σrx在接触面处增长速率增大，峰值位于外层壳体，径向位移ur在内层壳体中随着半径增大而增大，但在外层壳体中变化不大。此外，与层间固结接触相比，接触层的弹性特性使得位移ur、ux在接触面处产生突变，随着γ1的增大或xs1的减小，内外层壳体在接触面处的位移差异逐渐减小，相应的应力、位移幅值也逐渐减小，表明夹层刚度Kn、Kτ的增大使得壳体内应力位移减小。此外，文献［10］指出当 Kn→∞和Kτ→∞时，弹性层接触条件即转化为固结连接边界条件，在本例中相同厚度条件下γ1增大至0.005时，两种接触条件求得的应力、位移值较好的趋于一致(图中曲线3和曲线5)也表明了这一点。

3 结论

本文研究了轴对称纵向导波在具有较薄接触层的双层中空柱壳中传播频散特性，并通过算例分析了接触层参数对纵向L(0，1)模态下壳体内应力、位移分布的影响。结论如下:

(2)与层间固结接触条件相比，弹性接触层特性对纵波频散关系及壳体内应力位移的影响在波数η较大时较为显著，壳体内应力位移随着接触层厚度的减小和单位刚度Kn、Kτ的增大而减小，而受接触层泊松比影响较小。

［1］Lowe M J S.Matrix techniques for modeling ultrasonic waves in multilayered media［J］.IEEE Uffc，1995，42(4):525－542.

［2］Ryden N，Lowe M J S.Guided wave propagation in threelayer pavement structures［J］.Acoustical Society of America，2004，116(5):2902 －2913.

［3］James B，Rose J L.Guided wave resonance tuning for pipe inspection［J］.Journal of Pressure Vessel Technology，2002，124:303－310.

［4］Rose B J.Guided wave propagation in an elastic hollow cylinder coated with a viscoelastic material［J］.IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，2004，51(11):1547 － 1556.

［5］Achenbach J D.Wave propagation in elastic solids［M］.New York:North Holland，1984.

［6］Kuhn G J，Lutsch A.Elastic wave mode conversion at a solidsolid boundary with transverse slip ［J］.The Journal of the Acoustical Society of America.1961，33:949 －954.

［7］Valle C，Qu J M，Jacobs L J.Guided circumferential waves in layered cylinders［J］.International Journal of Engineering Science，1999，37:1369 －1387.

［8］张慧玲，尹晓春.光滑接触的双层复合圆筒中的周向导波［J］.船舶力学，2010，14(8):930 －937.ZHANG Hui-ling，YIN Xiao-chun.Guided circumferential waves in a double-layered hollow composite cylinder with a free-sliding interface［J］.Journal of Ship Mechanics，2010，14(8):930－937.

［9］Rokhlin S L，Wang Y J.Analysis of boundary conditions for elastic wave interaction with an interface between two solids［J］.The Journal of the Acoustical Society of America，1991，89(2):503－515.

［10］张慧玲.复合筒结构中的周向导波［D］.南京:南京理工大学，2008.82 －91.

［11］他得安，刘镇清，贺鹏飞.复合管状结构中超声导波的位移分布［J］.复合材料学报，2003，20(6):130 －136.TA De-an，LIU Zhen-qing，HE Peng-fei. Displacement distribution of longitudinal guided waves in composite pipes［J］.Acta Materiae Compositae Sinica，2003，20(6):130 －136.

［12］侯秀慧，邓子辰，周家喜，等.夹层圆柱壳中弹性波传播的辛特性分析［J］.固体力学学报，2010，31(4):363－368.HOU Xiu-hui， DENG Zi-chen， ZHOU Jia-xi ， et al.Symplectic analysis for elastic wave propagation in sandwich cylinder［J］.Chinese Journal of Solid Mechanics，2010，31(4):363－368.

［13］罗斯 J L著.何存富，吴斌，王秀彦译.固体中的超声波［M］.北京:科学出版社，2004.

［14］龚家元.水中覆阻尼层弹性板及柱壳中的漏lame波研究［D］.哈尔滨:哈尔滨工程大学，2010.

附录:系数矩阵A中元素aij取值如下: