减振器对井下钻具振动特性的影响分析

祝效华，胡志强

(西南石油大学 机电工程学院，成都 610500)

由于钻井是一个非常复杂的动态过程，钻具振动不可避免，在钻遇硬岩时振动尤为剧烈。受振动的影响，钻压和扭矩不能均匀地施加于井底岩石，并在钻具中产生较大纵向和剪切交变应力，引起井下钻具特别是MWD、LWD、RSS等精密仪器失效。此外，由于剧烈振动，钻头与井底岩石处于间歇性接触状态，使其有效破岩时间大幅度减小，影响钻井效率。为降低振动对井下钻具的危害，目前各油田普遍采用的方法是使用钻具减振器，但现场实践表明，使用减振器后，钻具振动并非都能得到明显减缓，因振动引起的钻具断裂事故仍时有发生［1］。

国外对钻具减振器的相关研究始于上世纪60年代。Kreisle等［2］运用Laplace理论分析了减振器对钻具纵向振动的影响。Skaogen等［3-5］利用MWD测得的振动数据分析了在一定转速范围内，不同减振器的减振效果。美国APS公司［6］研发了一种磁流变主动减振器(AVD)，并通过实验证明该减振器能提高机械钻速。国内学者对钻具减振器也做了大量研究，章扬烈［7］采用模拟实验的方法分析了减振器的使用效果，发现减振器能降低钻头动载，提高牙轮钻头钻井效率。李子丰［8］建立了钻具振动的数学模型，并采用分离变量法求解，提出减振器可能加剧井下钻具振动。张晓东等［9-10］等分别研究了减振器安装位置和刚度对其隔振效果的影响，分析结果对减振器现场使用具有一定的指导意义，但前者将井下钻具等效为一个七自由度系统、后者忽略了中和点以上钻具的振动特性，模型过于简化。目前尚无系统研究减振器阻尼和扭转减振器对井下钻具振动特性影响的文献公开发表。

本文基于虚功原理建立了井下钻具动力平衡方程，并采用数值模拟技术系统分析了纵向减振器特征参数(刚度、安装位置和阻尼)对钻杆(减振器上方钻具)和钻头(减振器下方钻具)振动特性的影响，确定了不同刚度纵向减振器最优阻尼取值范围，并探讨了扭转减振器的减振效果。分析结果对减振器的现场使用和优化设计，减缓井下振动，提高钻具使用寿命和钻井效率等具有重要意义。

1 钻具振动模型建立

1.1 基本假设

为便于分析研究，忽略次要因素，在不影响分析结果的前提下作如下假设:

(1)井下钻具为均质弹性直杆;

(2)钻具轴线与井筒轴线重合，忽略钻具的弯曲变形;

(3)地面以上的悬挂系统等效为一定刚度的无阻尼弹簧;

(4)略去静钻压和转盘匀速转动等静载荷的影响，仅分析井下钻具在井底振动激励下的响应。

1.2 力学模型

根据以上假设，并将井下钻具离散为n个微元，可以得到如图1所示的力学模型。

图1 井下钻具力学模型Fig.1 Mechanical model of down-hole drilling tools

1.3 动力平衡方程

根据虚功原理得出井下钻具动力平衡方程:

其中:M、C、K、P(t)分别为井下钻具系统的质量矩阵、阻尼矩阵、刚度矩阵和外载荷矢量(t)、(t)和u(t)分别表示井下钻具的加速度、速度和位移矢量。

引入地面和井底边界条件即可解得井下钻具的动力响应，且其响应分为自由振荡和稳态响应两个部分，由于阻尼的作用，自由振荡很快衰减至零，因此在分析中仅考虑稳态响应。

2 数值模拟

以L9井为研究对象，分析所用的钻具组合及相关参数:Ф311.1 mm三牙轮钻头+Ф229 mm减振器×5.78 m+Ф229 mm 钻铤 ×8.75 m+Ф229 mm 短钻铤 ×2.39 m+Ф203 mm 钻铤 ×9.23 m+Ф310 mm 稳定器×1.94 m+Ф203 mm 钻铤 ×9.35 m+Ф310 mm 稳定器× 1.71 m+Ф203 mm 钻铤 ×44.34 m+Ф127 mm 钻杆;钻具用钢弹性模量E=2.1 ×105MPa，密度 ρ=7.85×103kg/m3，泊松比0.3。

2.1 减振器对井下钻具纵向振动特性的影响

钻头纵向振动的位移幅值与井底岩石高低差密切相关，采用激励位移法，将悬挂系统顶端固定，井下钻具纵向振动的边界条件为:

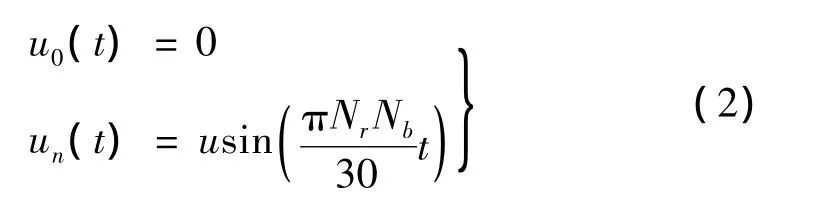
其中:u为波状井底高低差，Nr(1～200 r/min)为钻头转速，Nb为牙轮个数。

2.1.1 纵向减振器刚度对井下钻具纵向振动特性的影响

减振器刚度不同时，井口钻杆振幅和波动钻压幅值随转速变化曲线分别如图2和图3所示，从中可看出:

(1)减振器对井下钻具的各阶共振转速(曲线波峰对应的转速)有很大影响，且在减振器刚度k∈(3.5～7 kN/mm)范围内，井下钻具的低阶共振转速随减振器刚度降低而降低，高阶共振转速变化不大。

(2)在不同转速区域内，减振器对井下钻具振动幅值的影响不同:当Nr＜80 r/min时，减振器有加剧钻具振动的趋势，且减振器刚度越小，钻具振动越剧烈，L9井在该井段的钻进转速为65～70 r/min，靠近井下钻具的第三阶共振转速，是造成钻具断裂故事频繁发生的主要原因;当Nr＞80 r/min时，井下钻具尤其是钻头的响应曲线趋于平缓，减振器具有良好的隔振效果，且减振器刚度越小、转速越大，隔振效果越好。

2.1.2 纵向减振器安装位置对井下钻具纵向振动特性的影响

图4和图5是分别是减振器安装位置不同时，井口钻杆振幅和波动钻压幅值随转速变化曲线，从中可以看出:

(1)井下钻具的各阶共振转速随减振器距钻头距离增大而略有增大。

(2)当Nr＜50 r/min时，减振器离钻头越近、减振器下方钻具的质量越小，钻杆振幅越大;Nr＞50 r/min时，减振器离钻头越近、减振器下方钻具的质量越小，钻杆振幅越小。分析结果与文献［5］中的实测规律基本吻合。

(3)不同转速区域内，减振器安装位置对波动钻压幅值的影响有很大差异。从保护钻头的角度出发，当Nr＜50 r/min时，减振器应距钻头一定距离，随着转速增大，减振器最优安装位置趋向于逐渐靠近钻头。

图2 减振器刚度不同时钻杆振幅随转速变化曲线Fig.2 Shock absorber with different stiffness Amplitude of drill pipe versus rotary speed

图3 减振器刚度不同时波动钻压幅值随转速变化曲线Fig.3 Shock absorber with different stiffness Weight amplitude of bit versus rotary speed

图4 减振器安装位置不同时钻杆振幅随转速变化曲线Fig.4 Shock absorber in different installation site Amplitude of drill pipe versus rotary speed

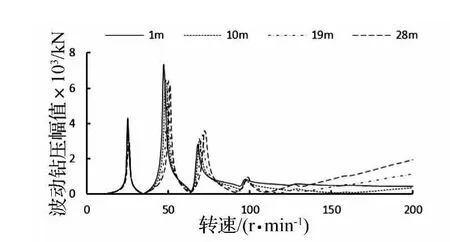
图5 减振器安装位置不同时波动钻压幅值随转速变化曲线Fig.5 Shock absorber in different installation site Weight amplitude of bit versus rotary speed

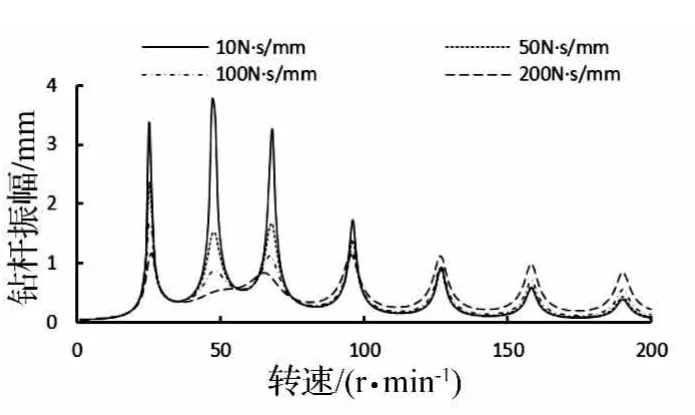
图6 减振器阻尼不同时钻杆振幅随转速变化曲线Fig.6 Shock absorber with different damping Amplitude of drill pipe versus rotary speed

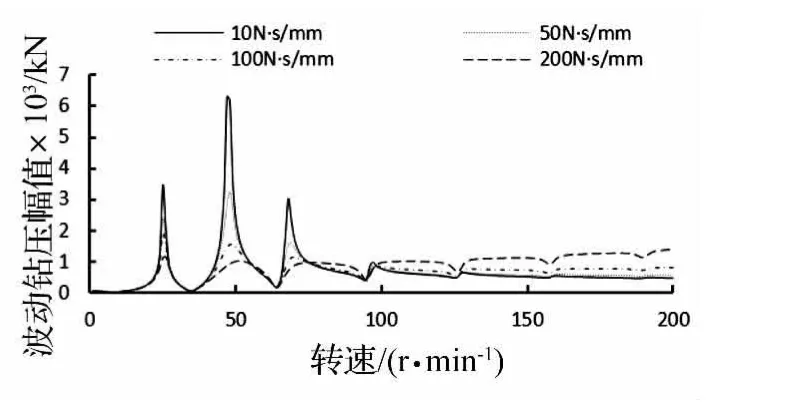
图7 减振器阻尼不同时波动钻压幅值随转速变化曲线Fig.7 Shock absorber with different damping Weight amplitude of bit versus rotary speed

2.1.3 纵向减振器阻尼对井下钻具纵向振动特性的影响

减振器阻尼不同时，井口钻杆振幅和波动钻压幅值随转速变化曲线分别如图6和图7所示(分析所用阻尼值参考自美国APS公司的AVD减振器)，从中可以看出在减振器阻尼c∈(10～200 N·s/mm)范围内:

(1)当Nr＜100 r/min时，在共振转速区域，井下钻具的共振幅值随减振器阻尼增大而明显降低;在非共振转速区域，减振器阻尼对井下钻具振动的影响很小。

(2)当Nr＞100 r/min时，随着减振器阻尼增大，井下钻具振动加剧、减振器减振效果降低。

由于不断变化的钻具组合(钻具长度)和复杂的井下环境，在实际钻井过程中，难以精确计算出井下钻具的各阶共振转速，尤其是在共振转速变得非常“密集”的深井中，因此选择阻尼适当的减振器，能大大增加井下钻具对转速的鲁棒性，尽最大可能减少因剧烈共振引起的钻具失效。

图8 钻杆振幅随减振器阻尼变化曲线Fig.8 Amplitude of drill pipe versus the damping of shock absorber

Nr∈(1～100 r/min)时，井口钻杆振幅和波动钻压幅值随减振器阻尼变化曲线分别如图8和图9所示，从中可以看出，减振器阻尼存在一个最优值ξ，当阻尼小于该最优值ξ时，井口钻杆和钻头响应的最大值和平均值都随减振器阻尼增大而明显减小;当阻尼大于ξ时，井下钻具响应的最大值随减振器阻尼增大而增大，平均值变化不大。

表1 不同刚度纵向减振器的最优阻尼取值范围Tab.1 The relationship between stiffness and optimum damping

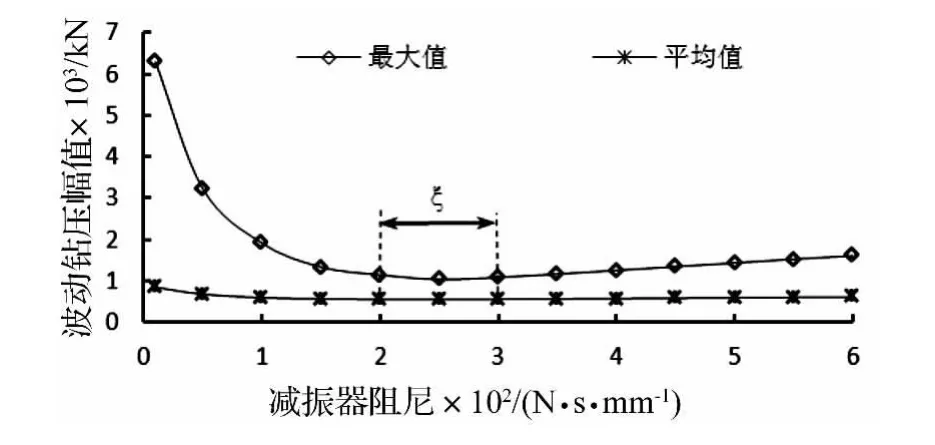
图9 波动钻压幅值随减振器阻尼变化曲线Fig.9 Weight amplitude of bit versus damping of shock absorber

表1为不同刚度纵向减振器最优阻尼的取值范围，从中可以看出，随着减振器刚度增大，其对应的最优阻尼值增大。

2.2 减振器对井下钻具扭转振动特性的影响

2.2.1 纵向减振器对井下钻具扭转振动特性的影响

根据牙轮钻头破岩过程中的力学性能与运动规律，将其与井底岩石之间的相互作用简化为质点在正弦曲线上的运动，并忽略静载，可以得到如图10所示的钻头与井底岩石相互作用模型。其中:W为波动钻压，Fr为波动扭矩，Fn为岩石对钻头的法向反作用力，Ff为岩石对钻头的摩擦力，v为钻头的运动方向，φ(0＜θ＜π/2)为钻头的运动方向与Fr之间的夹角。

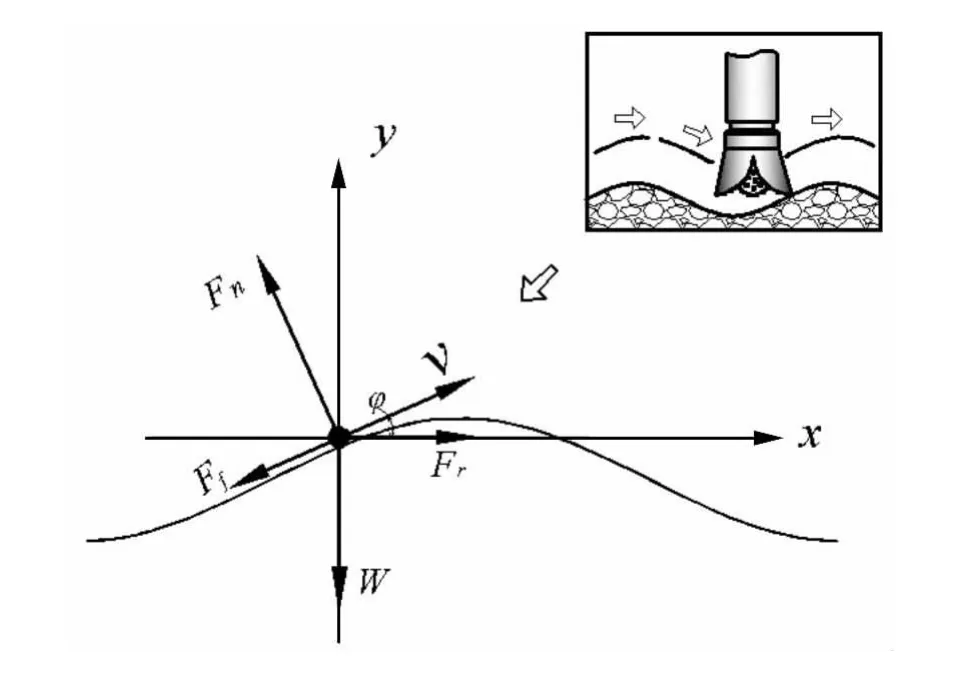
图10 钻头和井底岩石相互作用模型Fig.10 Interaction between bit and rock

参照钻头与井底岩石相互作用的力学模型，并根据牛顿第二定律得出钻头的受力平衡方程:

式中:μ为钻头与岩石之间的摩擦系数。

将式(4)代入式(3)解得:

由上述方程可以看出，在牙轮钻头破岩过程中，波动扭矩幅值主要由波动钻压幅值、钻头与岩石之间的摩擦系数μ以及夹角φ决定。在井底岩层一定的情况下，波动扭矩幅值与波动钻压幅值存在正相关性，因此纵向减振器对井下钻具的扭转振动和纵向振动具有相似的影响。

2.2.2 扭转减振器对井下钻具扭转振动特性的影响

目前对钻具扭转减振器的研究较少，且无相关标准，因此引用文献［7］中所提到的双向减振器作为分析对象。

由于井底钻具的扭转振动比地面系统剧烈得多，在分析井下钻具扭转振动时，假设地面系统固定。此外，由于钻头波动扭矩基本由钻头与岩石之间的摩擦系数和钻压决定，在分析中采用激励扭矩法，井下钻具扭转振动的边界条件为:

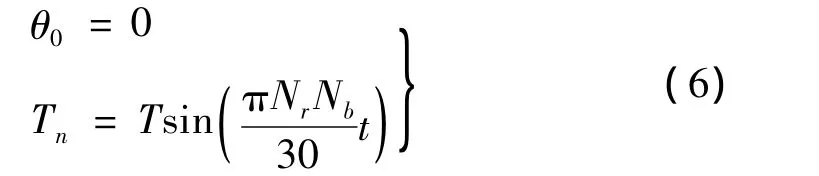
其中:T为钻头扭矩波动幅值。

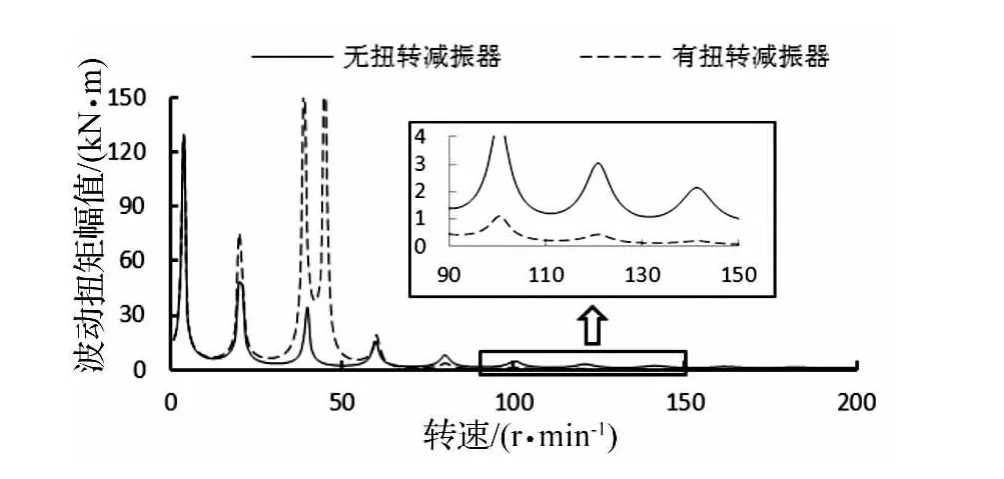
图11 有/无扭转减振器时上部钻杆波动扭矩幅值随转速变化曲线Fig.11 With or without torsion shock absorber Torque amplitude of top drill pipe versus rotary speed

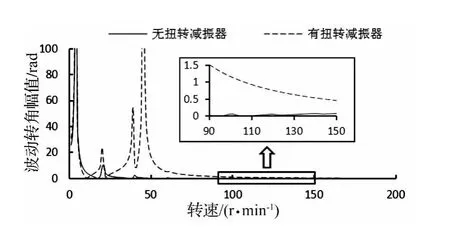
图12 有/无扭转减振器时钻头波动转角幅值随转速变化曲线Fig.12 With or without torsion shock absorber Rotor angle amplitude of bit versus rotary speed

图11为有/无扭转减振器时，井口钻杆波动扭矩幅值随转速变化曲线;图12为有/无扭转减振器时，井底钻头波动转角幅值随转速变化曲线。从中可以看出，当Nr＜65 r/min时，扭转减振器使钻杆和钻头扭转振动加剧，尤其是在Nr∈(30～50 r/min)范围内;当Nr＞65 r/min时，扭转减振器能降低上部钻杆波动扭矩幅值，但同时加剧了钻头处的扭转振动。

3 结论

根据牙轮钻头在破岩过程中的力学性能和运动规律，分析了纵向减振器特征参数(刚度、安装位置和阻尼)对井下钻具振动特性的影响，并探讨了扭转减振器的减振效果。结果表明:不同转速下，减振器对井下钻具振动特性的影响不同，同一转速下，其对钻杆和钻头振动的影响规律也可能存在差异;减振器阻尼的科学选择对提高井下钻具对转速的鲁棒性具有重要意义，且减振器最优阻尼值随其刚度增大而增大;纵向减振器对井下钻具的纵向振动和扭转振动具有相似的影响。在确定减振器最优特征参数时，建议在考虑转速的基础上增加对钻杆和钻头振动特性的关注。

［1］郑新权.隆9井-中国石油一口高难井［M］.北京:石油工业出版社.

［2］Kreisle L F，Vance J M.Mathematical analysis of the effect of a shock sub on the longitudinal vibrations of an oil well drill string［J］.SPE Journal，1970，10(4):349-356.

［3］Skaogen E，Kyllingstad A.Performance testing of shock absorbers［C］.SPE 15561，1986.

［4］ Skaugen E， Kyllingstad A， Aarrestad T A， etal.Experimental and theoretical studies of vibrations in drill strings incorporating shock absorbers［C］.WPC 22217，1987.

［5］Warren T M，Oster J H，Sinor L A，et al.Shock sub performance tests［C］.SPE 39323，1998.

［6］Wassell M E，Cobern M E，Saheta V.Active vibration damper improves performance and reduces drilling costs［J］.World Oil，2008:108-111.

［7］章扬烈.钻柱运动学与动力学［M］.北京:石油工业出版社，2001.

［8］李子丰.油气井杆管柱力学及应用［M］.北京:石油工业出版社，2008.

［9］张晓东，李 俊，梁红军.减振器安装位置对钻柱纵向振动的影响研究［J］.西南石油大学学报，2007，29(3):146-149.

ZHANG Xiao-dong，LI Jun，LIANG Hong-jun.Influence of shock absorberinstallation position on the drillstring longitudinal vibration［J］.Journal of Southwest Petroleum University，2007，29(3):146-149.

［10］何逸飞，郑 平，刘祚才，等.减振器减振效果的控制因素分析［J］.石油矿场机械，2008，37(11):33-36.

HE Yi-fei，ZHENG Ping，LIU Zuo-cai，et al.Analysis of controlling factors of damping effect of absorber［J］.Oil Field Equipment，2008，37(11):33-36.

［11］ Apostal M C，Haduch G A，Williams J B.A study to determine the effect of damping on Finite-Element-Based，Forced-FrequencyvResponse models for bottom hole assembly vibration analysis［C］.SPE 20458，1990.

［12］ Omojuwa E，Osisanya S，Ahmed R.Dynamic analysis of stick-slip motion of drillstring while drilling［C］.SPE 20930，2011.

［13］ Bailey J J，Finnie I.An analytical study of drillstring vibration ［J］.Journal of Engineering for Industry，Transaction of the ASME，1960，82(2):122-128.

［14］高 岩.三牙轮钻头钻进时钻柱纵向振动的特征［J］.石油学报，2000，21(6):93-96.

GAO Yan.Axial vibration performance of drillstring when drilling with three-cone bit［J］.Acta Petrolei Sinica，2000，21(6):93-96.

［15］朱才朝，谢永春，刘清友，等.牙轮钻头纵向横向扭转振动动力学仿真研究［J］.振动与冲击，2002，21(1):46-51.

ZHU Cai-chao， XIE Yong-chun， LIU Qing-you， et al.Dynamic simulation of roller cone bit system with lengthways，transverse and torsional vibrations［J］.Journal of Vibration and shock，2002，21(1):46-51.

［16］ Khulief Y A，Al-Naser H.Finite element dynamic analysis of drillstrings［J］.Finite Elements in Analysis and Design，2005，41:1270-1288.

［17］祝效华，贾彦杰，童 华.气体钻井钻柱振动特性及控制措施［J］.石油学报，2012，3(2):293-297.

ZHU Xiao-hua， JIA Yan-jie， TONG Hua. Vibrating characteristics of drill string in gas drilling and its control measures［J］.Acta Petrolei Sinica，2012，33(2):293-297.