基于信号共振稀疏分解的阶比分析及其在齿轮故障诊断中的应用

孙云嵩，于德介，陈向民，李 蓉

(湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082)

齿轮是传递动力和旋转运动的关键部件，广泛应用于各种机械设备之中。当齿轮出现点蚀、脱落和裂纹等局部故障时，将导致故障轮齿与其他轮齿滑动接触表面之间的润滑油膜破裂，产生冲击现象［1］。该冲击包含了齿轮局部故障的重要信息，但由于受齿轮振动信号传递路径(齿轮-轴-轴承-轴承座-测点)的影响［2］，测取的冲击信号比较微弱，往往淹没在齿轮、轴等机械零部件自身振动的周期谐波信号中，因此，如何从齿轮故障信号中有效地提取冲击是齿轮局部损伤诊断的关键。

近年来，许多学者致力于齿轮局部故障的冲击特征提取研究，取得了较多的研究成果。刘小峰等［3］根据瞬态冲击成分和平稳信号在时频空间内分布特征的不同，将代表齿轮故障特征的瞬态冲击从复杂的多分量振动信号中提取出来，该方法的提取效果较好，但计算量大，且阈值不好控制;杨富春等［4］根据冲击信号具有显著的非高斯特性来提取齿轮故障信号中冲击成分的频率特征，对恒转速的信号有较好的分析效果，但不适用于变转速情况;李友荣等［5］利用小波包将信号分解到不同频段，然后选择有效频段进行故障信号重构，提取齿轮故障信号中的周期冲击成分，在谐波成分与冲击成分的频率相差较大的情况下具有较好的冲击提取效果，但当两者频带重叠交叉时分析效果则不理想;袁静等［6］将相邻系数降噪思想引入到平移不变多小波中，揭示出了齿轮早期裂纹的微弱故障特征信息，降噪效果好，但自适应性不佳，对谐波成分抑制性不足。李辉等［7］在MOM机制的基础上，综合利用TH-MOM阈值更新策略、自适应字典选择等措施对传统MAC算法进行了改进，较好的提取了轴承多故障特征。

Selesnick［8］最近提出了信号共振稀疏分解方法，该方法根据信号中周期谐波成分与瞬态冲击成分品质因子(定义为中心频率与带宽的比值，用Q表示)的不同，将信号分解为包含周期谐波成分的高共振分量与包含瞬态冲击的低共振分量。周期谐波成分为窄带信号，具有高的品质因子，而瞬态冲击成分为宽带信号，具有低的品质因子，因而，根据品质因子的差异，可实现周期谐波成分与瞬态冲击成分的分离。当齿轮处于恒定转速时，低共振分量中的冲击将按照一定的时间间隔规律重复出现，但由于受电压波动、负载等影响［9-10］，齿轮往往处于非平稳转速下，导致低共振分量中冲击之间的时间间隔不均匀，并不满足频谱分析的平稳性要求［11］，因而，需预先对低共振分量进行平稳化。

工程实际中常采用阶比跟踪方法［12］来实现信号的平稳化，其基本思想是将时域非平稳振动信号进行等角度重采样，转化为角域平稳振动信号。常用的阶比跟踪方法有硬件阶比跟踪法、计算阶比跟踪法［13-14］、基于瞬时频率估计的阶比跟踪法［15］等。其中，基于瞬时频率估计的阶比跟踪法因无需安装角度编码盘、转速计等硬件，近年来得到了广泛的关注。而在基于瞬时频率估计的阶比跟踪法中，其核心问题是如何从原始振动信号中准确地提取出转速信号。线调频小波路径追踪算法［16］采用分段拟合的思想，能有效地提取信号中的转速信号。相对于峰值追踪算法，线调频小波路径追踪算法具有拟合精度高、抗噪能力强等优点，因而在机械故障诊断领域得到了应用［17-18］。

由于信号共振稀疏分解方法能有效地实现周期谐波成分与瞬态冲击的分离，凸显齿轮故障特征;而线调频小波路径跟踪算法能从原始振动信号中精确的估计出转速信号，因此，本文将信号共振稀疏分解方法，阶比跟踪方法和线调频小波路径追踪算法相结合，提出一种基于信号共振稀疏分解的阶比分析方法。该方法首先利用信号共振稀疏分解方法对齿轮振动信号进行分解，得到包含周期谐波成分的高共振分量和包含瞬态冲击成分的低共振分量，然后，采用线调频小波路径跟踪方法从齿轮振动信号中提取出转速信号，根据该转速信号对低共振分量进行等角度重采样，最后对角域重采样信号进行包络谱分析，根据包络谱中故障特征阶比进行齿轮故障诊断。应用实例表明，本文方法能有效地提取出变转速下的齿轮瞬态冲击成分，凸显齿轮故障特征。

1 信号共振稀疏分解方法

1.1 信号的共振属性

信号的共振属性用品质因子Q定义。Q越大，信号的频率聚集性越好，具有越高的共振属性;反之，Q越小，信号的时间聚集性越好，具有越低的共振属性。图1表明了信号共振属性的概念。图1左边为信号时域波形图，右边为对应的幅值谱图。图1(a)、(c)为单周期脉冲信号，品质因子Q较小，定义为低共振信号;图1(b)、(d)为持续多个周期的脉冲信号，品质因子Q较大，定义为高共振信号。图1(a)所示信号与图1(c)所示信号、图1(b)所示信号与图1(d)所示信号之间可通过时间尺度的变化互相转化，时间尺度的变化会引起脉冲信号频率发生变化，但对信号的共振属性没有影响，即具有相同的品质因子。所以高、低共振信号都可能同时包含了低频信号和高频信号。高共振信号可通过具有高Q的基函数来实现稀疏表示，而低共振信号则可通过具有低Q的基函数来实现稀疏表示。

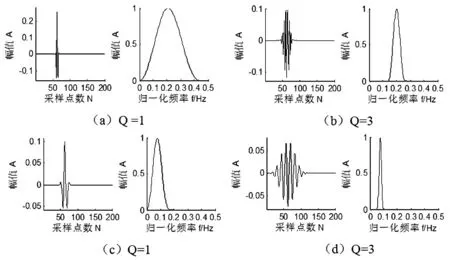
图1 不同品质因子信号的时域波形及频谱Fig.1 Signal with different quality-factor and the specrtum

传统的线性滤波方法按频带划分对信号进行分解，但当信号分量的中心频率相近且频带相互重叠时，如图1中(a)与(b)、(c)与(d)所示信号的中心频率重叠在一起，此时线性滤波方法就会失效，而信号共振稀疏分解方法从信号共振属性角度出发，综合考虑了信号中心频率与频率带宽因素，能有效分离中心频率相近且中心频率带相互重叠但具有不同品质因子的信号分量。

1.2 品质因子可调小波变换

二进制小波变换作为一种恒Q变换(其Q值由所选基函数确定)，在对分段光滑信号的稀疏表示中显示了其有效性，但由于其品质因子相对较低，频率分辨率不高，因而在对频率分辨率要求较高的信号分析中，二进制小波不适用。有理膨胀小波本质上为一种过完备的二进制小波变换，相对于二进制小波具有更高的品质因子和更高的频率分辨率。品质因子可调小波变换［7］与有理膨胀小波变换类似，具有完全离散、完美重构、适度完备、依赖于两通道滤波器组，并利用离散傅里叶变换计算等特点。但相对于有理膨胀小波变换，品质因子可调小波变换概念简单;利用基为2的快速傅里叶算法，计算更加高效;品质因子和冗余度更容易量化。

信号共振稀疏分解方法利用品质因子可调小波变换分别获取高Q变换与低Q变换的基函数库，并计算其相应的变换系数。可调品质因子小波变换通过带通滤波器组实现，其两通道滤波器组如图2所示。

图2 两通道滤波器组Fig.2 Two-channel filter banks

品质因子可调小波变换利用图2(a)所示两通道分解滤波器组以迭代的方式实现信号的分解，L层品质因子可调小波变换如图3所示，图3中Vjh表示信号经过第j层变换得到的高频系数，Vjl表示经过第j层变换得到的低频系数，j=1，…，L。

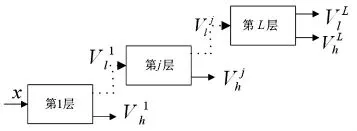
图3 品质因子可调小波变换图Fig.3 Plots with adjustable quality factor

1.3 高共振分量和低共振分量的分离

信号共振稀疏分解方法利用形态分量分析［7，19-20］将信号中各成分按振荡特性进行非线性分离，建立起高共振分量和低共振分量各自的最佳稀疏表示形式。

假定观测信号x可表示为两个信号x1与x2之和:

形态分量分析的目的即是从观测信号x中分别估计出源信号x1和x2。假定信号x1和x2可分别用基函数库(或框架)S1和S2(S1、S2具有低的相关性，本文中S1、S2分别表示为高、低品质因子可调小波的滤波器组)表示，形态分量分析的一种目标函数可表示为:

式中:W1，W2分别表示信号x1，x2在框架S1、S2下的变换系数;λ1、λ2为正则化参数，λ1、λ2的取值对分解出的高共振分量与低共振分量的能量分配有影响，给定λ1，增大λ2会使λ2所对应分量的能量减少;同时增大λ1、λ2的值，则会使残余信号能量增大。

在式(2)中，由于l1范数不可微、且参数较多，使得式(2)的求解变得困难。信号共振稀疏分解方法利用分裂增广拉格朗日搜索算法［8］，通过迭代更新变换系数W1，W2，使目标函数J最小化，最终实现高共振分量和低共振分量的有效分离。

假设目标函数J最小时，对应的高共振和低共振变换系数分别为，，则求取的高共振分量和低共振分量的估计值分别表示为:

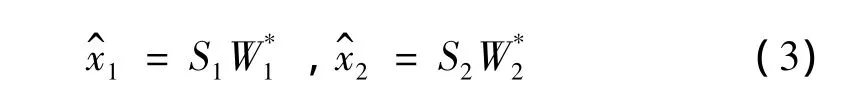
2 线调频小波路径追踪算法

展开系数an的大小反映了f(t)与基函数的相似程度［21］。

线调频小波路径追踪算法采用的多尺度线调频基元函数如下

式中:D 为基元函数库;haμ，bμ，I(t)为多尺度线调频的基元函数;I为动态分析时间段，I=［kN2-j～(k+1)·N2-j］，其中N为分析信号的采样长度，j为分析尺度系数，j=0，1，…2-j-1;Kaμ，bμ，I为归一化系 数，使得，aμ为频率偏置系数，bμ为调频率。根据采样定理，aμ+2bμt＜fs/2;1I(t)为矩形窗函数，当t∈I时，1I(t)=1，当 t∉I时，1I(t)=0。

式(5)定义的多尺度线性调频基函数在动态分析时间段内的瞬时频率为 aμ+2bμt。多尺度线性调频基函数通过对信号进行逐段投影分析，计算获得每个时间分析段内的最大投影系数和对应的线调频基元函数，该基元函数即为在时间分析段中与分析信号最为相似的频率成分，适合在小的动态分析时间段内逐段拟合频率呈曲线变化的频率。线调频基函数的多尺度特性使得它具有了动态匹配分析信号的特性，而基函数中包含的调频率信息则使得其适合分析频率呈曲线变化的非平稳信号。

当信号与多尺度线性调频基函数越相似时，其投影系数也越大，基元函数的能量也越大，因此要求找到一种动态分析时间段连接方法，在该连接方法下满足在整个分析时间内使连接的所有基元函数信号的总能量最大，即:

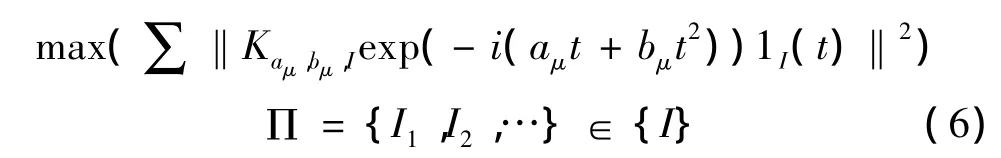
∏覆盖整个分析时间段，不能重叠，其对应的最大投影系数和基元函数分别为:

∏的连接方法应保证连接的基函数在整个分析时间段内的总能量最大。线调频小波路径追踪算法提出的连接算法如下:

(1)初始化。以i为时间支持区序号，d(i)为第i个时间支持区之前分解信号的总能量，pre(i)为连接到第i个时间支持区的前置时间支持区序号，e(i)为第i个时间支撑区最大投影系数对应的分解信号的能量，初始化时，置d(i)=0，pre(i)=0。

(2)对于动态分析时间段集合{Ii，i∈Z}中的每一个元素Ii，查找出与其相邻的所有下一个动态分析时间段集合{Ij}，即{Ij}中所有元素的起始时间与Ii相邻。如果:

有:

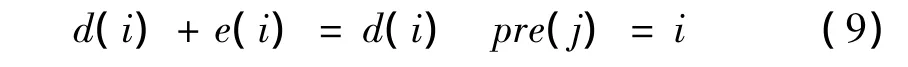
∏的连接方法可以保证在整个分析时间段内基元函数组合形成的信号与分析信号最为相似，而基元函数在动态分析时间支撑区∏={I1，I2，…}内的瞬时频率为 aμi+2bμiti，ti∈Ii，对应的线性直线连接形成的频率曲线则是对分解所得信号的瞬时频率估计。

3 基于信号共振稀疏分解的阶比分析

当齿轮发生故障时，振动信号主要由瞬态冲击成分和齿轮的啮合频率、转频等谐波成分组成。信号共振稀疏分解方法能够将瞬态冲击成分与谐波干扰成分进行分离，从而去除谐波干扰成分对故障诊断结果的影响。在进行非平稳齿轮振动信号分析时，线调频小波路径追踪算法可以有效的提取转速信号，将非平稳振动信号转化为角域平稳信号，从而满足信号分析对信号平稳性的要求，同样其提取的转速信号也能够将时域非平稳的瞬态冲击成分转化为角域平稳的瞬态冲击成分，以便利于故障诊断。因此本文首先用信号共振稀疏分解方法提取瞬态冲击成分，然后利用线调频小波路径追踪算法获得齿轮箱转速信号，根据转速信号对提取的冲击信号进行等角度重采样，再对角域冲击信号进行阶比分析，完成基于信号共振稀疏分解的阶比分析过程。主要分析步骤如下:

(1)对齿轮故障振动信号进行共振稀疏分解，将信号分解为高共振部分和低共振部分;

(2)利用线调频小波路径追踪算法对原信号进行瞬时频率估计，得到瞬时啮合频率，根据瞬时啮合频率求出瞬时转频;

(3)用三阶多项式对瞬时转频进行拟合，有:

a，b，c，d为三阶多项式系数，由最小二乘法拟合得到［14］;

(4)确定阶次跟踪的最大分析阶次Dmax;

(5)计算重采样后数据的长度N和等角度重采样的键相时标 Tn，根据求出的键相时标Tn，利用Lagrange线性插值公式对低共振分量进行插值，求出低共振分量在角域里对应于键相时标 Tn的幅值x(Tn)。其中N根据式(11)得出，键相时标 Tn根据式(12)得到，幅值x(Tn)根据式(13)得到。式(11)～(13)的表达式如下:

式中:T为时域采样的总时间，f(t)为频率拟合函数。

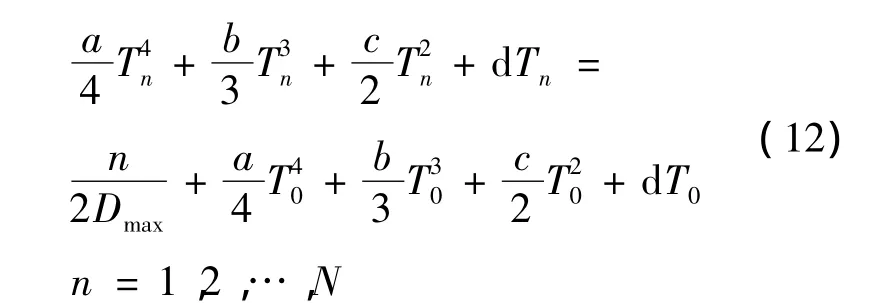
式中:T0为时域采样开始时间。

(6)对 x(Tn)(n=1，2，3，…，N)进行包络阶次分析，根据得到的低共振分量阶比谱进行故障诊断。

基于信号共振稀疏分解的阶比分析原理框如图4所示。

4 应用实例

4.1 断齿及正常齿轮分析

将齿轮箱故障试验台上的某一主动齿轮的一个齿进行破坏，即将某一主动齿轮切割一个齿，模拟齿轮断齿故障，在变转速下采集一组断齿齿轮振动信号。输入轴齿轮齿数为55，输出轴齿轮齿数为75，采样频率为4 096 Hz，采样时长为2 s，正常齿轮和断齿齿轮参数相同。图5为变转速条件下采集到的断齿齿轮振动信号时域波形，从中可以看出断齿信号存在间隔不均匀的冲击。

图4 基于信号共振稀疏分解的阶比分析原理框图Fig.4 Schematic of the order domain analysis method based on resonance-based sparse signal decomposition

利用共振稀疏分解方法对断齿振动信号进行分解，取高品质因子Q1为5，低品质因子Q2为1，结果如图6所示，图6(a)为高共振分量，即信号谐波分量，图6(b)为低共振分量，即提取的瞬态冲击，冲击的时序间隔并不均匀，具有非平稳性，很难直接看出有效信息。

图5 断齿齿轮实测信号Fig.5 Measured broken gear vibration signal

利用线调频小波路径追踪方法进行转频估计，得到转速信号如图7中所示。利用拟合转频将提取到的故障冲击信号角域平稳化，对平稳化后的冲击信号部分进行包络阶次分析，得到阶次谱结果如图8所示。当齿轮发生故障时，齿轮箱振动信号主要表现为以故障齿轮所在轴转频及其倍频为调制频率的啮合频率调制，且振动能量和包络能量较大。图8仅可见一个明显的峰值谱线，峰值1点坐标为(2，0.018 47)，说明调制频率为转频的2倍频，可见该齿轮发生故障，且无干扰分量。分析结果验证了本文所提出的基于信号共振稀疏分解的阶比分析方法的有效性。

为了进行对比，用线调频小波路径追踪算法对该断齿齿轮振动信号进行阶比分析，得到结果如图9。从图中可以看到有两个明显峰值谱线，峰值点1、2坐标分别是(0.757 9，0.061 05)、(2.021，0.131 2)，据此分析得齿轮调制频率为0.757 9倍频和2.021倍频，二倍频为齿轮故障引起的调制频率，但0.757 9倍频不是转频及其整数倍频。由于齿轮故障振动信号中存在一些谐波干扰信号，在解调时会作为干扰分量出现在阶比谱中，可以诊断0.757 9倍频为信号中的干扰成分造成的。在基于信号共振稀疏分解的阶比分析方法中，由于将瞬态冲击信号与谐波干扰信号分离，避免了干扰成分的影响，因此更有利于齿轮故障分析。

同样可以得到正常齿轮振动信号经过信号共振稀疏分解后的阶比谱如图10所示。峰值1、2、3、4点坐标分别为(1.022，0.002 485)、(2.022，0.002 737)、(4.044，0.002 439)、(5.044，0.002 057)，说明其调制频率分别为一倍、二倍、三倍、四倍等转频。但与图8相比，正常齿轮阶比谱中峰值明显相对较小。由于齿轮加工误差会引起的齿形误差等问题，导致齿轮在运转过程会引起一定程度的冲击，在振动信号分析过程亦会出现转频调制现象，但其能量小，不会对故障齿轮信号分析造成影响。

图6 断齿齿轮信号共振稀疏分解结果Fig.6 The resonance-based sparse signal decomposition results of the broken gear vibration signal

图7 线调频小波路径追踪算法拟合的断齿齿轮转频曲线Fig.7 The rotation frequency of the broken gear obtained by the chirplet path pursuit algorithm

图8 断齿齿轮低共振分量阶比谱Fig.8 The order spectrum of the low-resonance component of the broken gear

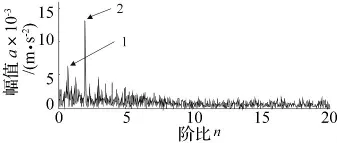
图9 断齿齿轮振动信号阶比谱Fig.9 The order spectrum of the broken gear

图10 正常齿轮振动信号低共振分量阶比谱Fig.10 The order spectrum of the low-resonancecomponent of the normal gear

4.2 轮齿裂纹故障分析

利用线切割技术在轮齿根处加工出宽0.1 mm、深3 mm的槽，并在无负载条件下模拟齿轮齿根裂纹。输入轴齿轮齿数为37，输出轴齿数为37，在变转速条件下利用加速度信号传感器拾取振动信号，采样频率为2 048 Hz，采样点数为4 096，在变转速情况下采集到的齿轮裂纹振动信号如图11所示。

利用共振稀疏分解方法对裂纹信号进行分解，取高品质因子Q1为5，低品质因子Q2为1，得到高共振分量如图12(a)所示，低共振分量如图12(b)所示。低共振分量冲击的时序间隔不均匀，具有非平稳性，难以直接看出有效信息。

图13为利用线调频小波路径追踪方法得到的转频曲线。利用拟合转频曲线对低共振分量等角度重采样，再对角域平稳信号进行包络阶次分析，得到阶次谱结果如图14所示。图14仅可见一个明显的峰值谱线，峰值1点坐标为(2，0.040 53)，说明调制频率为转频的2倍频，可见该齿轮发生故障，且无干扰分量。分析结果再次验证了本文方法的有效性。

为了进行对比，利用拟合转频曲线直接对裂纹齿轮振动信号等角度重采样，再对角域平稳信号进行包络阶次分析，得到结果如图15所示。从图中可以看到有两个明显峰值谱线，峰值点 1、2坐标分别是(0.537 9，0.050 76)、(2.005，0.097 75)，据此分析得齿轮调制频率为0.537 9倍频和2.005倍频，二倍频为齿轮故障引起的调制频率，但0.537 9倍频不是转频及其整数倍频，同样可以诊断0.757 9倍频为信号中的干扰成分造成的。从图14与图15的对比可以看出，本文方法能够有效分离瞬态冲击信号与谐波干扰信号，去除干扰成分的影响，更有利于齿轮故障分析。

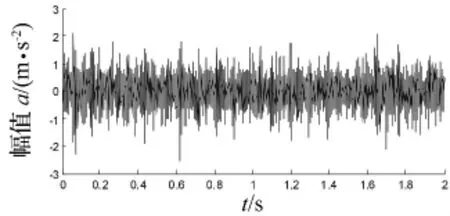
图11 轮齿裂纹振动信号Fig.11 Vibration signal of the cracked gear

图12 裂纹齿轮振动信号共振稀疏分解结果Fig.12 The resonance-based sparse signal decomposition results of the cracked gear vibration signal

图13 线调频小波路径追踪算法拟合的裂纹齿轮转频曲线Fig.13 The rotation frequency of the cracked gear obtained by the chirplet path pursuit algorithm

图14 裂纹齿轮振动信号低共振分量阶次谱Fig.14 The order spectrum of the low-resonance component of the cracked gear

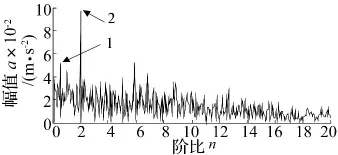
图15 裂纹齿轮振动信号阶比谱Fig.15 The order spectrum of the cracked gear

5 结论

本文将信号共振稀疏分解方法与线调频小波路径追踪算法相结合，提出基于信号共振稀疏分解的阶比分析方法，并将其应用于非平稳转速状态下的齿轮箱故障诊断。结合应用实例分析，得到如下结论

(1)信号共振稀疏分解方法能有效分离中心频率相近且中心频率带相互重叠但具有不同品质因子的信号分量。将共振分解方法应用于冲击故障特征提取，能够将瞬态冲击与谐波分量分离，去除干扰分量，提高瞬态冲击成分提取能力。

(2)将基于信号共振稀疏分解的阶比分析方法应用于实际齿轮振动信号分析，结果表明该方法能够将谐波分量与冲击分离，从而有效克服了干扰信号对齿轮故障诊断的影响，与线调频小波路径追踪算法结合，保证了阶比分析结果的准确性，为非平稳转速下齿轮箱故障的特征频率的提取、故障识别和诊断提供了一种新的分析方法。

［1］褚福磊，彭志科，冯志鹏，等.机械故障诊断中的现代信号处理方法［M］.北京:科学出版社，2009.

［2］丁 康，李巍华，朱小勇.齿轮及齿轮箱故障诊断实用技术［M］.北京:机械工业出版社，2005.

［3］刘小峰，柏 林，秦树人.基于自适应时频分解的瞬态冲击信号提纯［J］.机械工程学报，2008，44(11):166-170.LIU Xiao-feng，BO Lin，QIN Shu-ren.Transient impulse signalextraction based on self-adaptive time-frequency decomposition［J］. Chinese Journal of Mechanical Engineering，2008，44(11):166-170 .

［4］杨富春，周晓军，张志刚.基于滑动峰态算法的信号弱冲击特征提取及应用［J］.振动与冲击，2009，28(4):103-105，109.YANG Fu-chun，ZHOU Xiao-jun，ZHANG Zhi-gang.A new extraction method and its application for weak impulse characteristic based on sliding kurtosis algorithm［J］.Journal of Vibration and Shock，2009，28(4):103-105，109.

［5］李友荣，曾法力，吕 勇，等.小波包分析在齿轮故障诊断中的应用［J］.振动与冲击，2005，24(5):101-103.LI You-rong，ZENG Fa-li，LÜ Yong，et al. Gear fault diagnosis by using wavelet packet［J］.Journal of Vibration and Shock，2005，24(5):101-103.

［6］袁 静，何正嘉，王晓东，等.平移不变多小波相邻系数降噪方法及其在监测诊断中的应用［J］.机械工程学报，2009，45(4):155-160.YUAN Jing，HE Zheng-jia，WANG Xiao-dong，etal.Translation-invariant multiwavelets denoising using neighboring coefficients and its application to monitoring and diagnosis［J］.Journal of Mechanical Engineering，2009，45(4):155-160.

［7］李 辉，郑海起，唐力伟.基于改进形态分量分析的齿轮箱轴承多故障诊断研究［J］.振动与冲击，2012，31(12):135-140.LI Hui，ZHENG Hai-qi，TANG Li-wei.Bearing multi-fault diagnosis based on improved morphological component analysis［J］.Journal of Vibration and Shock，2012，31(12):135-140.

［8］Selesnick I W.Resonance-based signal decomposition:a new sparsity-enabled signal analysis method［J］. Signal Processing，2011，91(12):2793-2809.

［9］Lu B，Li Y Y，Wu X，et al.A review of recent advances in Wind Turbine condition monitoring and fault diagnosis［C］.Power Electronics and Machines in Wind Applications.IEEE，2009.1-7.

［10］Heyns T，Godsill S J，Villiers J P，et al.Statistical gear health analysis which is robust to fluctuating loads and operating speeds［J］.Mechanical Systems and Signal Processing，2012，27:651-666.

［11］李 辉，郑海起，杨绍普.基于角域平均和连续小波变换的齿轮故障诊断研究［J］.振动与冲击，2007，26(11):16-19.LI Hui，ZHENG Hai-qi，YANG Shao-pu.Gear fault diagnosis based on angle domain average and continuous wavelet transform［J］. Journal of Vibration and Shock，2007，26(11):16-19.

［12］Shao H，Jin W，Qian S.Order tracking by discrete gabor expansion［J］.IEEE Trans on Instrumentation and Measurement，2003，52(3):754-761.

［13］Bossley K M，Mckendrick R J，Harris C J，et al.Hybrid computed order tracking［J］.Mechanical Systems and Signal Processing，1999，13(4):627-641.

［14］Saavedra P N，Rodriguez C G.Accurate assessment of computed order tracking［J］.Shock and Vibration，2006，13(1):13-32.

［15］郭 瑜，秦树人，汤宝平，等.基于瞬时频率估计的旋转机械阶比跟踪［J］.机械工程学报，2003，39(3):32-36.GUO Yu，QIN Shu-ren，TANG Bao-ping，et al.Order tracking of rotatingmachinerybased on instantaneousfrequency estimation［J］.Chinese Journal of Mechanical Engineering，2003，39(3):32-36.

［16］Candès E J.Detecting highly oscillatory signals by chirplet path pursuit［J］.Applied and Computational Harmonic Analysis，2008，24(1):14-40.

［17］刘 坚，彭富强，于德介.基于线调频小波路径追踪阶比跟踪算法的齿轮箱故障诊断研究［J］.机械工程学报，2009，45(7):81-86.LIU Jian，PENG Fu-qiang，YU De-jie.A new order tracking method based on chirplet path pursuit and its application to gearbox fault diagnosis［J］.Chinese Journal of Mechanical Engineering，2009，45(7):81-86.

［18］陈向民，于德介，罗洁思.基于线调频小波路径追踪阶比循环平稳解调的齿轮故障诊断［J］.机械工程学报，2012，48(3):95-101.CHEN Xiang-min，YU De-jie，LUO Jie-si.Gear tooth fault diagnosis by using order cyclostationary demodulating approach based on chirplet path pursuit［J］.Chinese Journal of Mechanical Engineering，2012，48(3):95-101.

［19］Starck J L，Moudden Y，Bobina J，et al.Morphological component analysis:an adaptive thresholding strategy［J］.Image Proceedings of IEEE，2007，16(11):2675-2681.

［20］Wright S J，Nowak R D，Figueiredo M A T.Sparse reconstruction by separable approximation［J］.IEEE Trans.on Signal Processing，2009，57(7):2479-2493.

［21］罗洁思，于德介，彭富强.齿轮箱故障振动信号的阶比多尺度形态学解调［J］.机械工程学报，2010，46(11):114-120，128.LUO Jie-si，YU De-jie，PENG Fu-qiang.The order multiscale morphology demodulation of the vibration signal of a fault gearbox with rotating speed fluctuation［J］.Chinese Journal of Mechanical Engineering，2010，46(11):114-120，128.