基于SIMULATION的龙门横梁有限元模态分析

山东法因数控机械股份有限公司 韩立光 路永军 孙科科

1.引言

龙门横梁是龙门式数控钻床一个极其重要的大件，它起着支撑钻削动力箱和连接立柱等关键零部件的作用。钻削动力箱通过滚动导轨副将钻削过程中受到的动态钻削力传递给龙门横梁。由于钻削工程中载荷变动较大，机床在工作状态下将承受不稳定复杂剧烈的振动。龙门横梁作为重要连接件，如果在工作中发生共振，则将严重影响工件加工质量，同时降低钻削刀具使用寿命。对龙门横梁进行动态特性的深入研究和振动稳定性的研究，分析其动态薄弱环节及结构优化设计等工作都是建立在模态固有频率和振型等动态特性的基础上而完成的［1］。

有限元分析法是目前一种比较可靠的分析方法，分析精度较高。本文利用SIMULATION有限元分析软件对龙门横梁建立动力学模型，并对龙门横梁的动态特性进行分析，求解出其振动的前5阶固有频率和振型等动态特性参数，为整机的优化设计及振动稳定性等分析提供科学的依据［2］。

2.有限元模态分析理论

对于一般多自由度的结构系统而言，任何运动皆可以由其自由振动的模态来合成。有限元的模态分析就是建立模态模型并进行数值分析的过程。模态分析的实质就是求解具有有限个自由度的无阻尼的运动方程的模态矢量。根据弹性力学中的有限元法，经分析可得龙门横梁在笛卡儿坐标系中的运动微分方程:

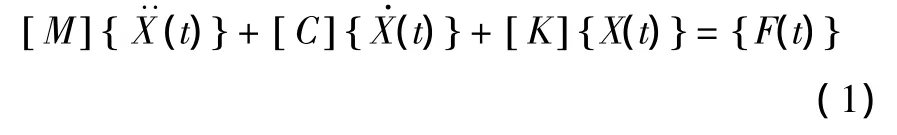
式中[M]﹑[C]和[K]分别为弹性系统的质量矩阵、阻尼矩阵和刚度矩阵，均为n阶方阵;n为节点自由度数;分别为加速度向量、速度向量和位移向量;(F{t})为动激励载荷向量。

因结构阻尼较小，对固有频率和振型影响甚微，可忽略不计。在这种情况下，分析结构的固有频率与振型问题转化为求解特征值与特征向量问题。那么，忽略结构阻尼，则由 (1)式可得横梁振动系统的特征方程为:

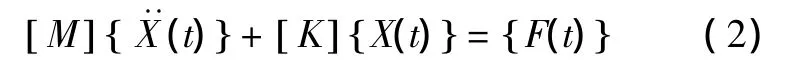
而弹性系统的自由振动又可以分解为一系列简谐振动的叠加，式中[ ]M﹑[]K均为实数对称矩阵。方程具有下列简谐运动形式的解:

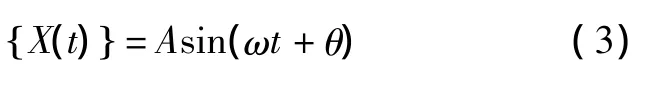
式中A为自由振动时结构各节点的振幅向量。此特解表示系统内各个坐标偏离平衡值时均以同一频率ω和同一初始相位角θ作不同振幅的简谐运动。将 (3)式代入 (2)式，化作矩阵[]K和[]M的广义特征值问题:

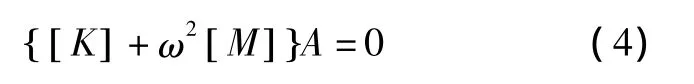
因为A为振幅自由振动时结构各节点的振幅向量。振动客观存在，故其值不为零，所以上式简化为:

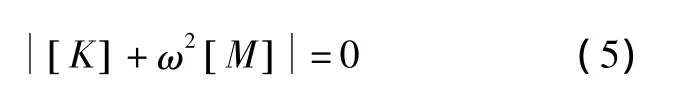
式 (5)是关于ω2的n次方程，解此方程可得结构的n个固有频率;ω2称为广义特征值，对应于每一个固有频率ω。由式 (4)可以确定一组各节点的振幅值A，称为广义特征向量。系统按第i阶固有频率所作的振动称作系统的第i阶模态:

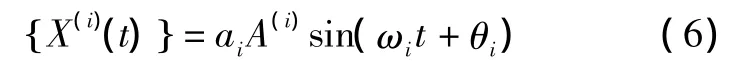
式中ai﹑θi为任意常数，取决于初始运动状态。列阵A(i)表示系统作第i阶主振动时，各坐标振幅的相对比值，此值由系统的物理性质确定，与初始运动状态无关。系统的固有频率和对应的模态完全由系统的物理参数矩阵[K]和[M]确定，为系统的固有特性。

从以上分析可知，龙门横梁的模态分析问题的实质即为求式 (5)中的ω2和式 (4)中A的解的问题，是一个广义特征值、特征向量问题［3］。

3.三维有限元模型的建立

建立准确而可靠的龙门横梁有限元计算模型是一项极为重要的工作。该龙门横梁采用Q235-A碳钢板焊接。内部采用肋板与加强筋交错的封闭箱形结构。将三维模型进行适当的简化与处理，可以在很大程度上节约计算时间与成本。模型的简化主要遵循以下原则:

(1)简化功能件和非承载构件。

(2)压缩部件上的螺纹孔、锥销孔等对模态影响甚小的特征。

(3)对于一些结构上的孔、台肩、凹槽、翻边，在截面形状特性等效的基础上尽量简化，对截面特性影响不大的特征予以忽略。

按照以上简化原则，运用SOLIDWORKS建立的龙门横梁三维模型，如图1所示:

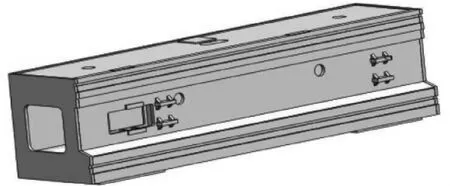
图1 有限元分析三维模型图

4.有限元模态分析

(1)建立频率算例。建立一个新的算例，算例类型制定为频率算例。建立算例后，在算例中指定部件材料属性。该处龙门为焊接件，材料采用Q235-A，弹性模量E=2.1e+011，泊松比μ=0.28，密度ρ=7800kg/m3

(2)模型网格划分。有限元分析前需对模型进行网格划分。网格划分是有限元前处理中的主要工作，也是整个有限元分析效果的关键所在。网格的优劣对整个结构分析的有效性和可靠性具有全局性的影响。网格的类型及疏密同样取决于分析的目的与精度要求。网格划分得越精细，即每个单元大小越小，模型的计算结果越精确;但是这样复杂的有限元模型将会花费大量的人力、物力在设计前的处理、数据准备、数据计算、数据整理和后处理上，考虑到计算的经济性，应适当选择网格大小。本文的网格划分注意了以下几点:

①自动划分和人工干预相结合。边角处自动过渡，提高计算精度。

②划分网格时检查单元质量，及时修正，以免计算结果出现大的误差。

③有限元网格与结合几何特征的协调性。

生成网格模型如图2所示:

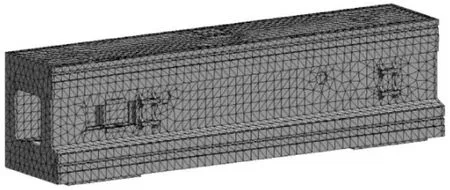
图2 模型网格图

(3)施加约束载荷。建立了网格后，还要模拟龙门横梁的实际约束情况。龙门横梁是通过下底面的螺栓孔与立柱连接。因此在这些螺纹孔施加固定约束，模拟螺栓连接。由于重力始终客观存在，并且可能对机构的形状及其形态属性造成很大的影响。故本处考虑重力影响，给部件施加重力引力作用。施加约束载荷后，如图3所示。

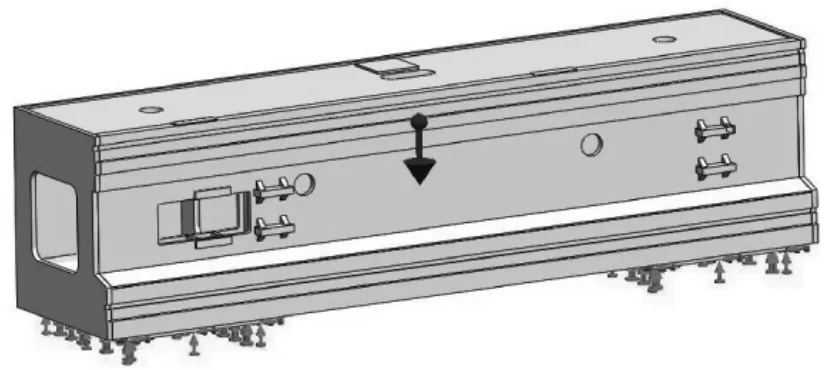
图3 施加约束图

(4)有限元分析与结果验证。由于结构的振动可以表达为各阶固有振型的线性组合，其中低阶的振型对结构的动力影响程度比高阶振型大得多。因此，低阶振型决定了结构的动态特性。对龙门横梁的研究主要关注对其影响较大的低阶模态。经过计算，此处取计算结果的前5阶振型模态。同时，用激振器对横梁进行正弦扫频激励，在其上布置20个检测点，拾取振动信号［4］。得到的计算结果与实验值对比如附表所示。

横梁前5阶固有频率与振型结果验证

前5阶振型图如图4所示:

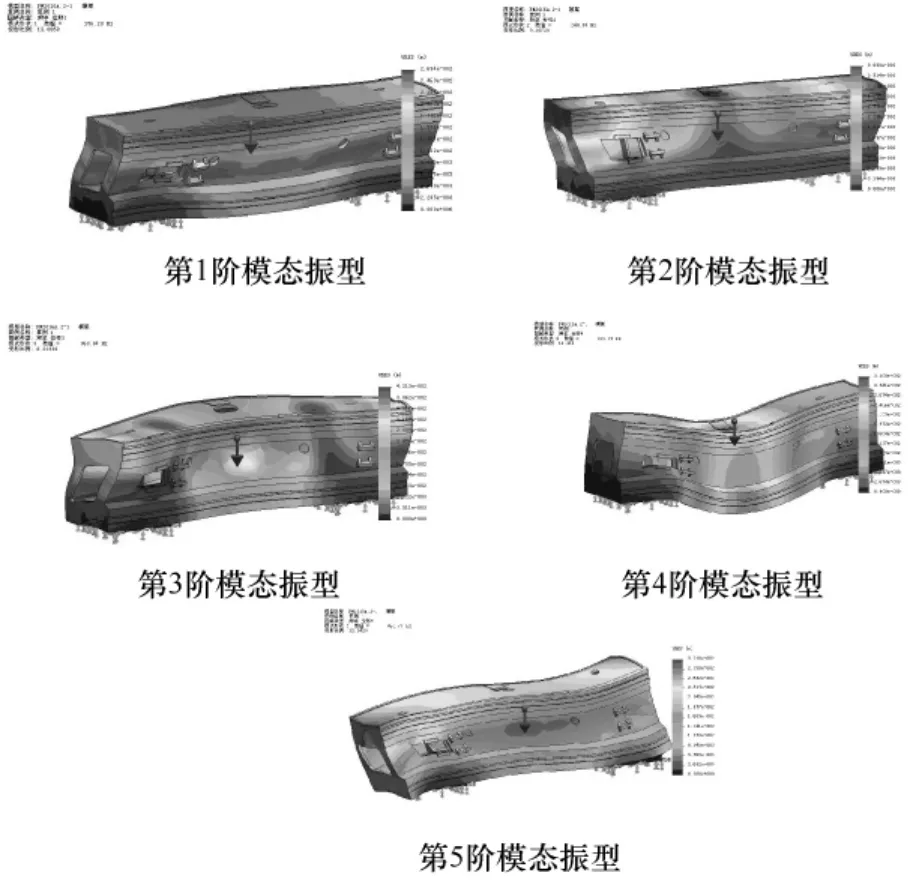
图4 前5阶振型图

从表中可以看出，计算结果与实验值较吻合，最大误差为第4阶模态振型，误差值为3.25%，在可接受范围之内。通过模态振型图中可以看出，振幅较大的且对加工有较大影响的为第1阶与第3阶模态振型。由这两个模态振型可以看出前后方向的摆动是该件的薄弱环节。该摆动振动也将在刀具加工过程中加快刀具磨损，如引起共振，甚至会出现崩刀现象。为增强前后方向刚度，可考虑增加前后壁板筋板和增加前后壁板厚度来弥补该方向刚度的不足［5］。经改进后，实际生产中工作状况较为理想，加工质量完全符合要求。

5.结论

在设计及结构优化改进阶段进行有限元模态分析是现代机械设计发展的趋势。本文基于有限元模态分析基本理论，建立了数控钻床龙门横梁的模态分析有限元模型，并计算了其在重力状态下的振动响应。所建有限元模型的计算结果同龙门横梁模态试验结果吻合很好，为该零部件详细设计和改进优化提供了理论依据，保证了设计的安全性，节省了整机成本。□

［1］ BeitzW，Kuttner K H.Mechanical Engineering-Manual.Berlin:Sp ringer Publishing Company，1987:3-7.

［2］林有希，高诚辉，高济众.大型机床动态特性的整机有限元分析.福州大学学报，2003(2):69-72.

［3］白化同，郭继忠.模态分析理论与实验［M］.北京:北京工大学出版社，2001.

［4］张玉琴，冯山岭，张淑红;桥式起重机的动力学模型与仿真计算 ［J］;重型机械科技，2005(3):1-3.

［5］朱岳东，张志军.基于动力学特征的车铣机床横梁的优化设计［J］.沈阳工业学院学报，2004，23(4):11-13.