基于Logistic回归模型的人口预测分析*

张小乐，黄晶霞

(1.楚雄师范学院数学系，云南 楚雄 675000;2.云南大学信息学院，云南 昆明 650031)

1.Logistic回归模型参数估计的研究意义

Logistic回归模型不仅可以应用于人口预测，还可用于医疗卫生、社会学、经济学等各个领域。在统计研究过程中，我们经常会遇到因变量为虚拟变量的情形，例如，在人口预测中生存率与死亡率、发病与未发病、性别比例问题。这时用线性回归模型的方法对此类问题进行研究已不再可行，而logistic回归模型可同时分析包含离散变量和连续变量的多个自变量，并能有效地分析自变量之间的交互作用，为多个自变量与因变量之间的相互关系提供一个定量描述。

本文在介绍Logistic回归模型的基础上，基于数值微分和最小二乘曲线拟合对Logistic回归模型进行了参数估计，这种方法对人口、资源、环境等的发展和预测具有应用价值.只要满足Logistic生长过程的事物，就可以采用Logistic函数预测，而在用Logistic函数进行预测的时候，本文中的估计方法就能发挥作用。

2.Logistic回归模型介绍

Logistic模型是1938年Verhulst－Pearl在修正非密度方程时提出来的，他认为在一定的环境中种群的增长总存在一个上限，当种群的数量逐渐向着上限上升时实际增长率就要逐渐地减少，因而也被称为 Verhulst－Pearl方程［1］。

人口问题是影响我国发展的重要因素，准确预测出未来人口的发展趋势有重要的指导意义，我们考虑种内对资源的竞争，自然资源、环境条件等因素对人口的增长起阻滞作用，且随着人口的增加，阻滞作用越来越大。

我们记时刻t的人口为x(t)，并将x(t)看作连续、可微的函数。记初始时刻(t=0)的人口为x0.假设人口增长率为常数r，也就是说单位时间内x(t)的增量等于r乘以x(t)。我们考虑t到t+△t时间内人口的增量，则有

令△t→0，则得到x(t)满足如下的微分方程

阻滞作用体现在对人口增长率r的影响上，使得r随着人口数量x的增加而下降.若我们把人口增长率r表示为人口数量x的函数r(x)，则r(x)是减函数，于是(2)式可写为

设r(x)是x的线性函数，即

这里的r表示人口很少时(理论上设x=0)的增长率，即人口不受环境和资源限制的固有增长率。为了明确参数s的意义，引入最大人口容量xm，即自然资源和环境条件所能容纳的最大人口数量。则当x=xm时，人口的增长率为零，即增长率r(xm)=r－sxm=0，从而得到，于是(4)式可改写为

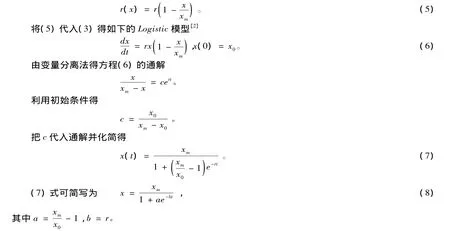
3.Logistic回归模型的参数估计

Logistic回归模型的参数估计的方法有很多，如极大似然估计、最小二乘估计、稳健估计、Bayes估计等等。本文用数值微分和曲线拟合法对logistic模型进行参数估计，并进行实证分析。

由Logistic模型的解(8)中可知，只要对参数xm，a，b进行估计即可，主要方法和步骤如下:

(1)首先求xm.对(6)式变形得到

(2)求参数a、b.将 (8)式变形为

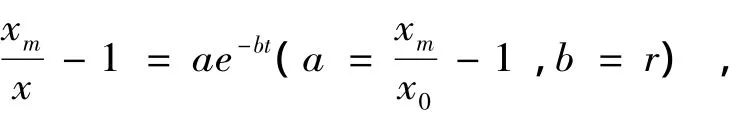
4.Logistic人口模型在人口预测中的应用

根据中国统计局在《统计年鉴》中公布的“1950—2010”年人口统计数据，本文只选取1980年到2005年的总人口数据(见表1)来拟合。

表1 1980—2005年中国人口数据(万人)

首先运用数值微分得到年增长率的值，然后再利用Matlab软件进行拟合［6］。

通过Matlab软件画出散点图(见图1)可以看出该图是一条单调函数的图像，且是指数型的，因此可以选用一次多项式进行拟合。

图1 1980—2005年拟合数据点

由表一中的数据估算出 xm=15.14(单位:亿)，a=0.5726，b=0.05073，从而得到中国人口的Logistic回归模型的具体表达式为

通过Matlab软件进行拟合可以直观地看到数值的变化情况(见图2)，预测的数据和实际数据曲线拟合得比较好。

图2 1980—2005年数据点与拟合曲线

于是求出预测中国人口的具体公式

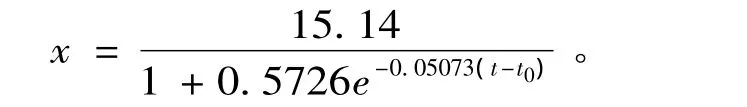
我们取1980年的人口总数为x0=9.8705(注:单位:亿)。

根据上式可以计算2000和2005年的人口数:

当t=20时，

误差都较小，说明预测结果比较准确。

下面来预测2015年的人口总数，即取t=35，则

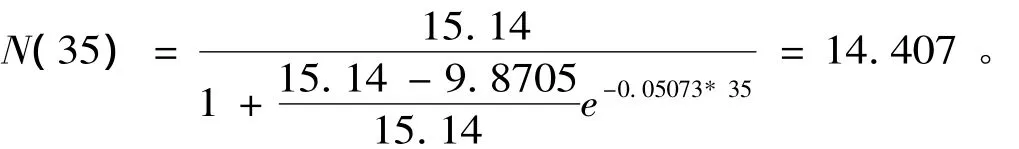
以此类推，我们可以估算出未来几年的中国人口数(见表2)。

表2 由上述公式可估算未来2015—2040年的中国总人口数:(单位:亿)

5.小结

本文基于数值微分和最小二乘曲线拟合对Logistic回归模型进行了参数估计，这种方法对人口、资源、环境等的发展和预测具有应用价值，由此计算了我国2000年到2005年总人口数的误差情况，并预测了2015年—2040年我国的人口总数。只要满足Logistic生长过程的事物，就可以采用Logistic函数预测，而在用Logistic函数进行预测的时候，本文中的估计方法就能发挥作用。

［1］姜启源.谢金星.叶俊.数学模型［M］.北京：高等教育出版社，2003：12—14.

［2］马修斯 (Mathews，J，H)，芬克 (Fink，K.D.).周璐.数值方法［M］.北京：电子工业出版社，2010：12—14，207—208，261—264.

［3］李秋红.何先平.数学模型在人口增长中的应用［J］.太原师范学院学报，2008，7(2)：55—56.

［4］李华中.Logistic模型在人口预测中的应用［J］.江苏石油化工学院学报，1998，10(2)：32—33.

［5］邵晓峰.张克新.黄冈市人口增长模型的研究［J］.数学的实践与认识，2008，38(13)：97—101.

［6］任玉杰.数值分析及MATLAB实现［M］.北京：高等教育出版社，2007：213—216.