一维光子晶体的电场分布特性＊

王 婧，巴 诺，吴向尧，刘晓静，张斯淇，李 宏，马 季，董 贺

（吉林师范大学物理学院，吉林四平 136000）

一维光子晶体的电场分布特性＊

王 婧，巴 诺，吴向尧，刘晓静，张斯淇，李 宏，马 季，董 贺

（吉林师范大学物理学院，吉林四平 136000）

推导出任意角度的入射光在一维光子晶体中传播的电场分布公式，分析一维光子晶体的电场分布特性.数值分析表明，入射光角度、光子晶体介质层排列方式、缺陷层和缺陷层折射率均对一维光子晶体电场分布特性产生不同的影响.

一维光子晶体；电场分布；缺陷层

光子晶体是人工制造的新型光学材料，1987年由Yablonovitch［1］和John［2］首次提出，因为该光子晶体能够有效地抑制光的自发辐射，降低噪声和能量的损耗，可作为优良的光传导介质，所以在物理学界引起了广泛的关注［3］.与半导体能带结构相似，当引入缺陷时，在光子晶体禁带中会出现缺陷态，从而导致光子的局域化.光子晶体的缺陷或杂质在带隙中产生定域的电磁波模式［4－5］，具有非常广泛的用途.

笔者以目前已有的光垂直入射时的透射率及色散关系等研究结果为基础，推导出光任意角入射时的透射率及反射率的精确表达式和光任意角入射时一维光子晶体内部电场强度分布的解析式，并对一维光子晶体的电场分布特性进行了详细的研究，分别讨论了一维光子晶体介质层排列方式、缺陷层位置、入射光角度和缺陷层折射率对一维光子晶体的电场分布特性的影响，为不同的一维光子晶体应用需求提供了理论依据.

1 光任意角度入射时的传输矩阵及透射率

对一维光子晶体，光在各介质层中均沿直线传播，只考虑TE波（E偏振与入射面垂直），已知电磁场边值关系：在介质交界面的切向方向上的电场强度和磁场强度是连续的.图1中E0和H0是界面Ⅰ上侧的场矢量，EⅠ和HⅠ是界面Ⅰ下侧的场矢量，EⅡ和HⅡ是界面Ⅱ下侧的场矢量.界面Ⅰ上方Ei1，Et1，Er1分别为电场分量入射光波，透射光波和界面Ⅰ下方入射到界面Ⅰ的光波［6］.

图1 任意角度的入射光在一维光子晶体介质中的传播

对于界面Ⅰ，Ⅱ上方，由电场和磁场的边值关系可知：

其中：xA和xB分别为A，B2点在x坐标的分量；xB＝xA＋tan·a（a为界面Ⅰ和界面Ⅱ之间的介质层A厚度）；n1为A的折射率.令则（3）式为

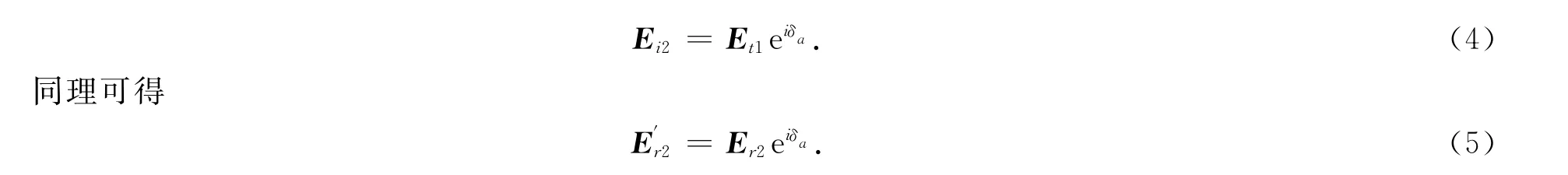
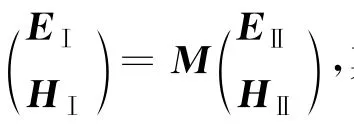
（8）式即为光在半个周期介质层中的传播矩阵.令介质层A，B的厚度分别为a，b，折射率分别为n1，n2，折射角分别为，，且由折射定律可知则入射角为的光在2个半周期介质层A中的传输矩阵为

于是1个周期的传输矩阵M为

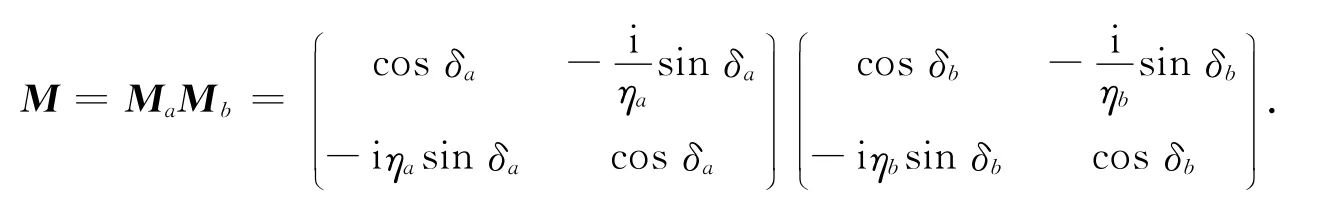
对于第N个周期，电场强度EN，EN＋1和磁场强度HN，HN＋1满足的关系式为

由（9）式最终可得到任意入射角的光在N个周期光子晶体中的特征方程为

其中M＝M1M2...MN＝MaMbMaMb...MaMb.

任意角度时的透射系数t、透射率T和反射系数r和反射率R分别为

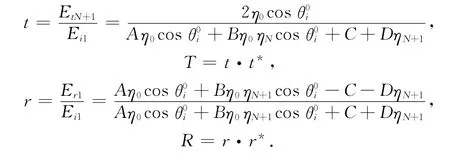
2 任意角度的入射光在一维光子晶体中的场强分布

由任意入射角的光在一维光子晶体中的传播矩阵可得

其中：N为第N周期；ΔzN为光在第N周期内的传播距离；E0，H0分别为入射电磁场强度，分别是光在第N周期内的电场和磁场强度.光在一维光子晶体内场强分布如图2所示.

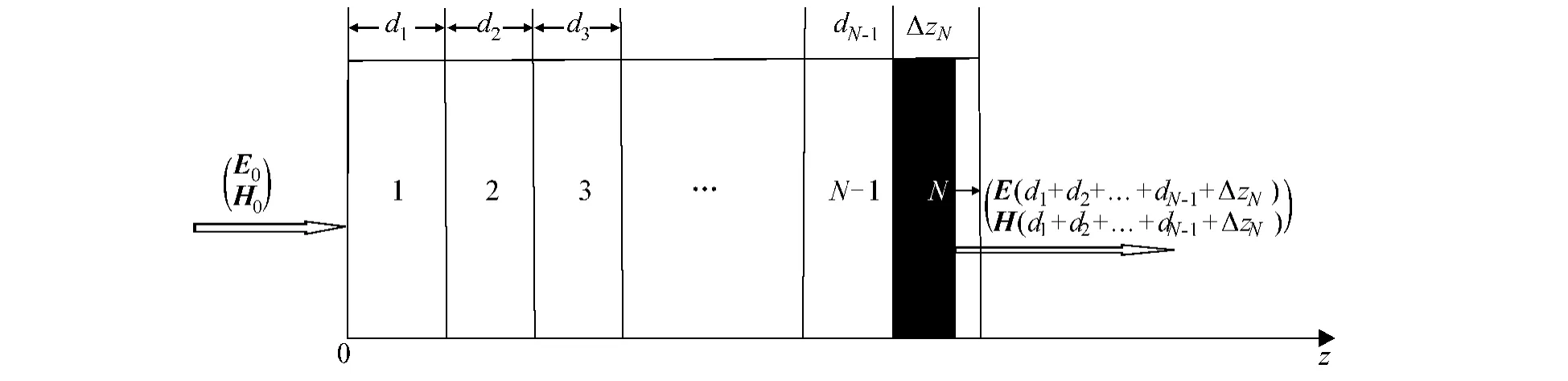
图2 光在一维光子晶体内场强分布

运用相应变换可得

由（10）至（12）式即可得到得任意角入射的光在一维光子晶体中的电场分布公式为

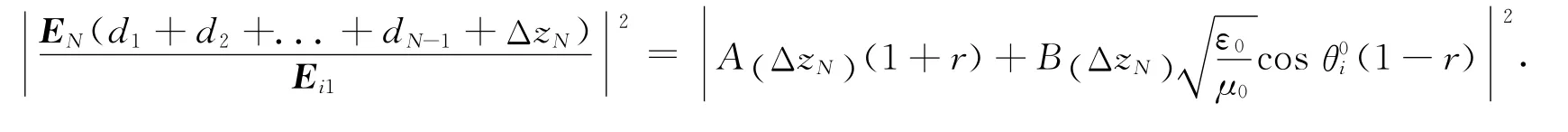
3 数值分析

文中讨论的一维光子晶体的A，B介质层分别由Si和Al2O3构成，折射率分别为n1＝3.42，n2＝1.766，介质层厚度分别为a，b，光学厚度n1a＝n2b＝λ0／4，中心波长λ0＝679×10－9m，对应角频率ω0＝2πc／λ0，c为真空中光速.

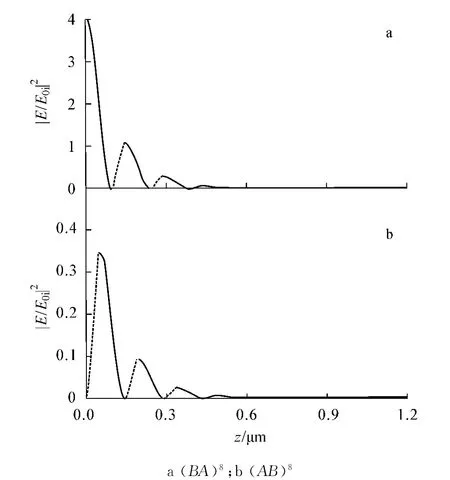
图3 光在不同结构的一维光子晶体中的场强分布曲线（θ＝0°）

图3为垂直入射的光在（BA）8，（AB）8结构的一维光子晶体中传播的场强分布曲线，横轴表示光在一维光子晶体中的传播位置z，纵轴表示光在不同位置所对应的场强与入射场强比值的模方，虚线为光在介质层A中光的场强分布曲线，实线是介质层B中光的场强分布曲线，入射光角频率ω＝ω0.从图3可看出：无论A，B介质如何排列，光在无缺陷一维光子晶体中传播时，其电场分布总是在A介质层中逐渐增强，B介质层中逐渐减弱.已知na＞nb，即在无缺陷的一维光子晶体中，光在相对折射率较大的介质中传播时，其电场分布总是呈增长趋势，而在相对折射率较小的介质中传播时，其电场分布总是呈减弱趋势.结果表明，垂直入射的光在（BA）8结构的一维光子晶体中的场强明显高于（AB）8结构的一维光子晶体中的场强.

图4为垂直入射的光在（AB）6D（BA）6，（BA）6D（AB）6结构的含缺陷一维光子晶体中传播的电场分布曲线.其中横纵轴坐标和虚实线含义同图3，黑粗线为光在缺陷层中传播的场强分布曲线，缺陷层D均相同，折射率nd＝1.457，光学厚度ndd＝λ0／2，入射光角频率ω＝ω0.

图4 光在不同结构的一维光子晶体中的场强分布曲线（θ＝0°）

从图4可发现：（1）当在一维光子晶体中加入缺陷后，光在A，B介质中的场强分布趋势发生了变化，无论A，B介质如何排列，光在含缺陷一维光子晶体中传播时，在缺陷层前的介质中，其电场分布总是在A介质层中逐渐减弱，B介质层中逐渐增强，而在缺陷层后的介质中，其电场分布总是在A介质层中逐渐增强，B介质层中逐渐减弱.（2）垂直入射的光在（AB）6D（BA）6结构的一维光子晶体中的场强明显高于（BA）6D（AB）6结构的一维光子晶体中的场强，但在缺陷层内场强的分布情况不同，前者虽然最大值较高，但其在缺陷层内分布趋势是先减弱后增强，在缺陷层中心处场强趋近0，后者场强最大值虽然无前者高，但其在缺陷层内分布趋势是先增强后减弱，在缺陷层中心处场强达到最大值.

比较图3，4还可发现，若一维光子晶体掺入缺陷层，则缺陷层附近的电场强度会得到明显增强，其增强程度与光子晶体结构有关.

图5为不同入射角的光在（AB）6D（AB）6结构的含缺陷一维光子晶体中传播的电场分布曲线，其中横纵轴的含义同图3.图5中黑粗线为光在缺陷层中传播的场强分布曲线，缺陷层D均相同，折射率和入射光角频率同图4，光学厚度ndd＝λ0／4.由图5可发现，对相同结构的含缺陷层一维光子晶体，逐渐增大其入射光角度，其场强分布随之逐渐减小.

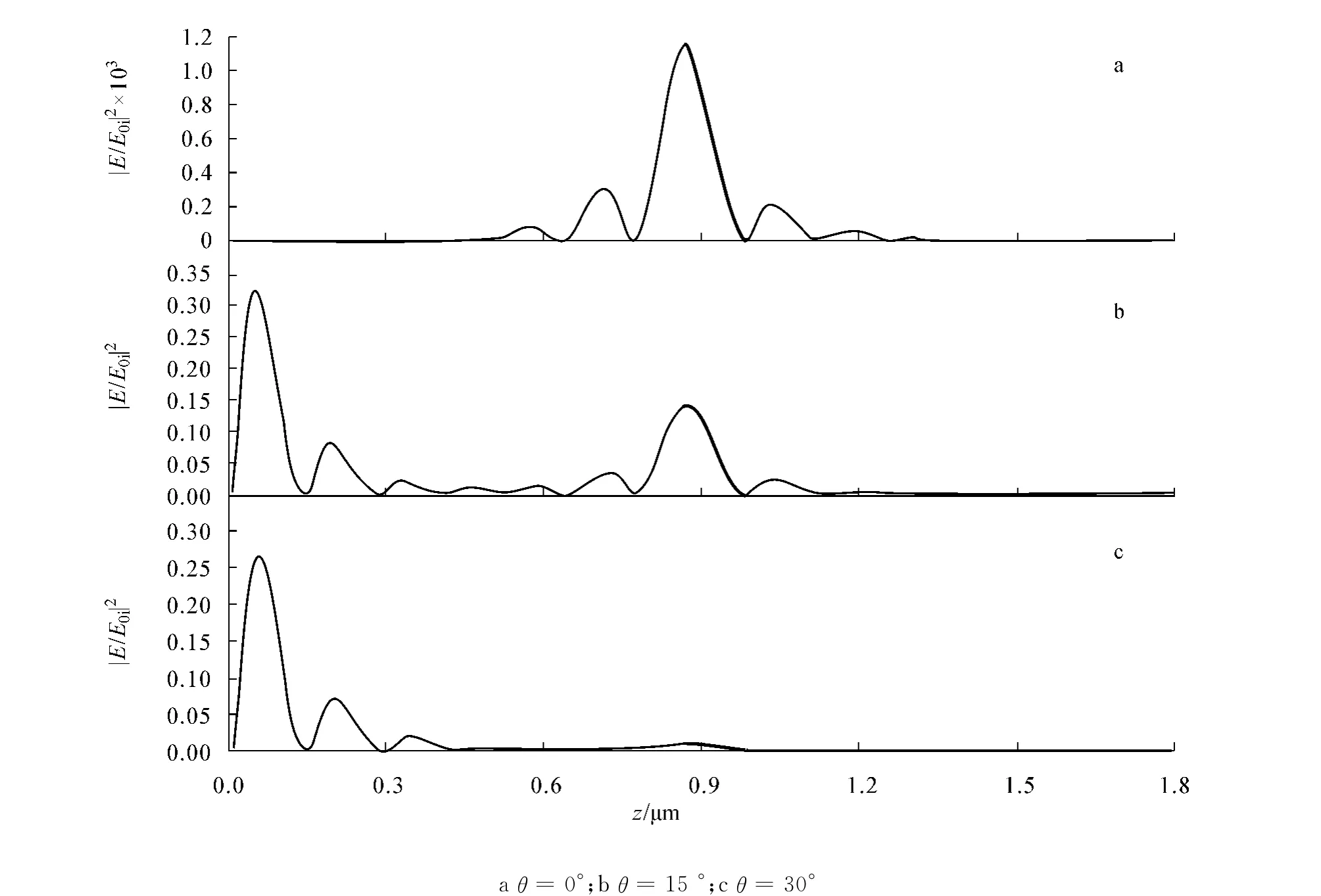
图5 不同角度入射光在（AB）6 D（AB）6结构的一维光子晶体中的场强分布曲线

图6为光在3种不同折射率的缺陷层一维光子晶体中传播的场强分布曲线，结构均为（AB）6D（AB）6，缺陷层折射率nd分别为1.457，2.55和4，光学厚度均为ndd＝λ0／4，入射光角频率均为ω＝2ω0，入射光角度θ＝30°.图6中黑粗线为光在缺陷层中传播的场强分布曲线，其中横纵坐标含义同图3.比较图6中不同缺陷层折射率nd下的电场分布可发现，随缺陷层折射率逐渐增大，缺陷层处的场强随之逐渐减小.

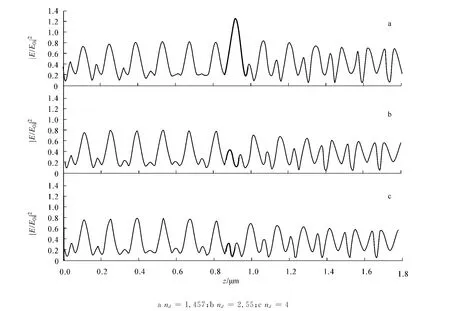
图6 不同nd条件下入射光在（AB）6 D（AB）6结构一维光子晶体中的场强分布曲线

4 结语

对任意角度入射的光在一维光子晶体中传播的透射率、电场分布公式进行推导，并利用推导公式对一维光子晶体的场强分布进行数值分析，结论如下：

（1）在无缺陷的一维光子晶体中，无论A，B介质如何排列，光在折射率较大的介质中传播时，其电场分布总是呈增长趋势，而在折射率较小的介质中传播时，其电场分布总是呈减弱趋势；垂直入射的光在（BA）8结构的一维光子晶体中的场强明显高于（AB）8结构的一维光子晶体中的场强.

（2）当在一维光子晶体中加入缺陷层后，光在A，B介质中的场强分布趋势发生了变化，无论A，B介质如何排列，光在含缺陷层一维光子晶体中传播时，在缺陷层前的介质中，其电场分布总是在A介质层中逐渐减弱，B介质层中逐渐增强，而在缺陷层后的介质中，其电场分布总是在A介质层中逐渐增强，B介质层中逐渐减弱.垂直入射的光在（AB）6D（BA）6结构的一维光子晶体中的场强明显高于（BA）6D（AB）6结构的一维光子晶体中的场强，但在缺陷层内场强的分布情况不同.

（3）对相同结构的含缺陷层一维光子晶体，场强分布随入射光角度增大而减小.

（4）一维光子晶体缺陷层附近的场强随缺陷层折射率增大而减小.

［1］ YABLONOVITCH E.Inhibited Spontaneous Emission in Solid－State Physics and Electronics［J］.Physical Review Letters，1987，58（20）：2 059－2 062.

［2］ JOHN S.Strong Localization of Photons in Certain Disordered Dielectric Superlattices［J］.Physical Review Letters，1987，58（23）：2 486－2 489.

［3］ 汤炳书，戴丽莉.二维周期复合介质构成的光子晶体能带结构［J］.吉首大学学报：自然科学版，2001，22（4）：63－68.

［4］ SAJEEV JOHN.Photonics：Light Control at Will［J］.Nature，2009，460：337－337.

［5］ RUSSELL P.Photonic－Crystal Fibers［J］.Science，2003，299：358－362.

［6］ 刘晓静，张伯军，王 婧，等.一维光子晶体中光场分布特性分析［J］.物理学报，2012，61（23）：237 801.

（责任编辑 陈炳权）

Electric Field Distribution Properties of One－Dimensional Photonic Crystals

WANG Jing，BA Nuo，WU Xiang－yao，LIU Xiao－jing，ZHANG Si－qi，LI Hong，MA Ji，DONG He
（Institute of Physics，Jilin Normal University，Siping 136000，Jilin China）

The electric field distribution formula of the transmitted incident liqut at arbitrary angle in onedimensional photonic crytals is deduced.The electric field distribution properties of one－dimentional photonic crystals are thus researched.The research shows that the incident angle，permutation of dielectric mode of photonic crystals，defect mode and defect mode refractive index can make different influences on the election field distribution in one－dimensional photonic crystals.

one－dimensional photonic crystals；electric field distribution；defect mode

O734

A

10.3969／j.issn.1007－2985.2013.03.00

1007－2985（2013）03－0039－07

2013－03－15

国家自然科学基金资助项目（11247201）

王 婧（1987－），女，吉林白山人，吉林师范大学物理学院硕士研究生，主要从事凝聚态理论物理学研究

吴向尧（1965－），男，安徽安庆人，吉林师范大学物理学院教授，博士，主要从事凝聚态理论物理学研究，E－mail wuxy2006＠163.com.