电锤冲击系统的波动力学研究＊

刘德顺，杨志高，杨书仪

（湖南科技大学先进矿山装备教育部工程研究中心，湖南 湘潭 411201）

引 言

电锤是将电能转变为冲击能，在混凝土、楼板、砖墙和石材上钻孔的一种常用手动工具。在其工作过程中，通过电动机将电能直接或者间接转变为冲锤的动能，冲锤以一定速度撞击冲杆，通过钻头作用于工作对象上，使其发生破碎并形成孔眼。撞击在瞬间完成，产生峰值极大的应力波脉冲，具有力放大功效。

在电锤这类利用撞击原理工作的冲击机械中，参与撞击的各个部件在撞击瞬间同时发生位移和变形，因而必须应用弹性动力学理论予以解释。又由于大多数冲击机械中各个冲击部件呈杆状，可以应用弹性动力学中一维波动力学理论进行近似分析，这不仅使冲击机械动力学建模和分析变得更简捷和直观，而且其分析精度可以达到工程要求［1，2］。所以，冲击机械波动力学研究成为该领域最为常见的方法。

Hustrulid等应用波动力学对凿岩冲击系统中应力波的传播规律、应力波波形与冲击能量传递效率的关系等问题进行了系统的研究［3］。Lundberg等分析了冲击系统中各个部件与工作介质力学特性的匹配关系，编制了冲击系统撞击凿入全过程的数值模拟程序［4］。徐小荷、刘德顺、邹定详等对冲击系统中应力波的产生和传播、各冲击部件动态响应特性以及工作介质的力学建模也进行了广泛研究［5～7］。刘德顺等基于特征线法和入反射波法分别描述了应力波在变波阻杆中的传播规律，提出了根据弹性杆上一点状态矢量依次计算钻头波阻的反演原理与计算方法，并对两种反演方法进行了验证与讨论［8，9］。刘德顺等对应用于采掘工程、建筑工程和加工工程等行业的冲击机械及其研究成果进行了系统梳理，提出了以弹性杆为核心元件的4元件冲击系统动力学建模方法，并根据冲击系统力学模型中所包含的独立的弹性杆件数将常见的冲击机械系统分为一元、二元和三元冲击系统［5］。以凿岩机械为代表的二元冲击系统波动力学研究颇多，但鲜见有电锤这类三元冲击系统波动力学研究报道。

1 电锤冲击系统波动力学建模

1．1 电锤冲击系统部件建模

根据电锤的结构特点和波动力学理论，可将电锤组成冲击系统的诸部件抽象为3个弹性杆部件，如图1所示。在工作中，冲锤以初速度v0接触并撞击冲杆，冲杆、钻头与工作对象均为紧密接触。

图1 电锤冲击系统结构Fig．1 The structure of an electric hammer impact system

在力学模型中，弹性杆被抽象为有质量和弹性的细长杆，如图2（a）所示。假设杆在变形时它的截面始终保持为平面，说明杆的截面上只受轴向应力。也就是说，弹性杆中的任一点的位移均满足一维波动方程式中u为杆中质点（截面）的位移，c为杆材料的纵波波速。

图2 力学模型中的基本元件Fig．2 The basic components in mechanical model

实际上，2个冲击部件之间接触并非同时全面接触，而是存在一个由小变大的接触面局部变形过程，工程上可以将2个相撞部件接触面的局部变形抽象为无质量的虚拟弹簧［5］，如图2（b）所示。弹簧的力学方程可表示为

式中u1，u2分别为弹簧元件两端的位移；k为撞击面的局部变形系数。

这里需要特别指出的是，通常在应用波动力学分析冲击机械时，习惯视压应力为正；并且弹性杆之间只能传递压应力，而不能传递拉应力；当弹性杆两个接触面上力等于0时，该面就处于自由状态，称之为自由面，也就是说自由面上作用力为0。

1．2 工作对象建模

混凝土、砖墙和岩石等工作对象的动力学特性对整个电锤冲击系统有着重要影响。一方面它作为冲击系统的一个重要边界条件，需要用它来定解波动方程，计算冲击凿入过程；另一方面，研究工作对象的力学特性，为预测凿进速度、电锤冲击系统各部件与工作对象的合理匹配关系提供依据。对于岩石、混凝土等脆性工作对象，电锤冲击系统工作端的作用力与凿深（位移）一般呈线性关系，如图3所示。从数学角度而言，这种线性关系可以用如下函数来描述

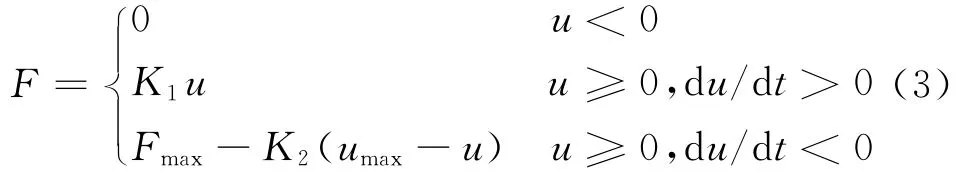
式中K1，K2分别为工作介质的加载系数和卸载系数；F为凿入力；u为凿入深度；Fmax，umax分别为最大凿入力与最大凿入深度。

图3 力－凿深曲线Fig．3 The force－penetration relationship curve

1．3 电锤冲击系统的性能指标

为了评估电锤冲击系统的性能，这里定义凿入深度为电锤单次撞击中工作端的最大位移量umax，它表征了电锤冲击系统的生产效率；定义电锤的效率η为冲击系统对工作对象所作的功与冲锤的动能之比值，它表征了电锤的能量利用率。

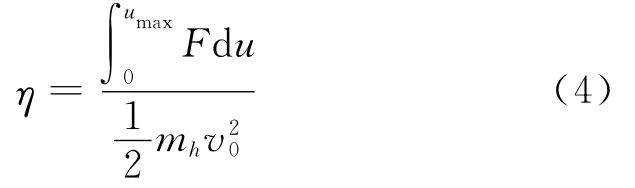
式中mh为冲锤的质量，v0为冲锤的初始撞击速度。

2 电锤冲击系统数值计算方法

2．1 离散处理

对于具体的电锤冲击系统，由于其部件结构形状、边界条件复杂，很难直接得到波动方程（1）的解析解，而只能采用离散数值计算方法求得数值解。在数值计算时，选定时间步长τ，由于应力波在弹性杆中的传播速度为c，那么相应的空间步长（单元轴线长度）为δ＝cτ。将冲击系统中各个弹性杆沿轴线离散成等长的若干单元，并按顺序从左至右给各离散界面编号。数值计算中，时间步长越小，单元长度越小，计算结果的精度越高。单元长度选取应根据冲击系统总长度与冲击部件形状结构来确定。在冲击系统长度较短或冲击部件形状结构复杂时，单元长度应尽量取得小些，以便获得更为精确的计算结果。

对波动方程（1）采用行波法求解，即认为在每个离散单元中同时作用这相向而行的两个波：顺波和逆波。用符号Pi，j，Qi，j表示单元界面上顺波受力值与逆波受力值，其中第一个下标i表示单元位置（i＝1，2，3，…），第二个下标j表示时间（j＝1，2，3，…）。用Fi，j表示单元界面上力作用力值，vi，j表示单元界面速度，它们之间存在如下关系

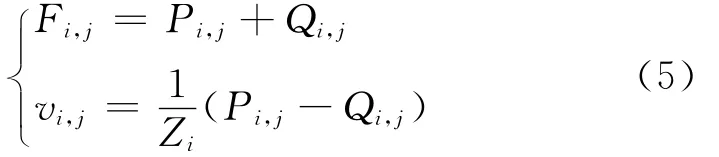
2．2 初始值的确定

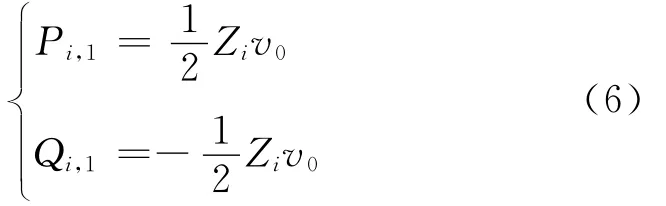
式中Zi为冲锤i单元的波阻。撞击发生后，顺、逆两波在撞击界面按透反射原理进行传播。

2．3 应力波传播

波动方程（1）的解由向右传播的顺波P和向左传播的逆波Q叠加而成。而无论是顺波还是逆波，它们在冲击部件中传播时，会在波阻发生变化的单元界面上发生应力波的透射、反射，根据透反射规律就可以得到冲击部件各个界面各个时刻的顺波、逆波。为了表示的方便，根据应力波的传播规律，用Pi－1，j－1，Qi＋1，j－1分别表示到达界面的顺波与逆波，用Pi，j，Qi，j分 别 表 示 越 过 界 面 之 后 新 的 顺 波 与 逆波，如图4所示。

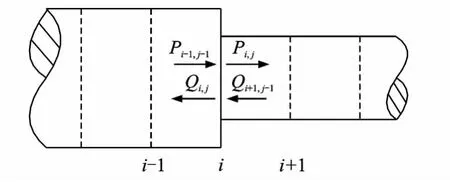
图4 应力波在波阻突变界面的传播Fig．4 Propagation of stress wave in the interface of impedance saltation

根据透反射关系可得

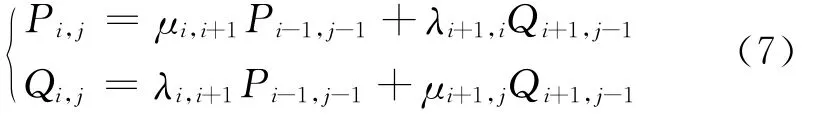
这里将一个波阻为Zi的单元向波阻为Zi＋1的单元传播时透射系数和反射系数表示为

式中μi，i＋1为透射系数，λi，i＋1为反射系数。

应力波在通过波阻发生改变的界面传播时，在界面两侧的作用力和速度分别相等，根据式（5）有

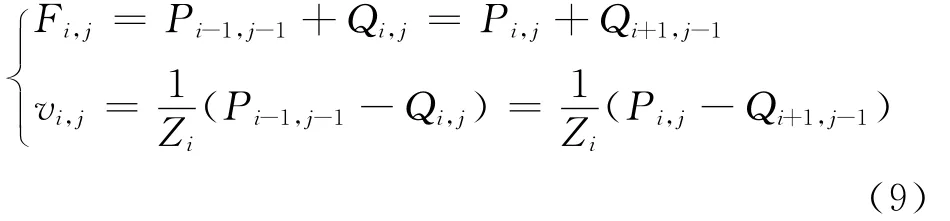
2．4 自由面

当部件界面未受到其他部件及其界面约束时，该界面就为自由面。在冲击系统中，冲锤的非撞击面即左端面始终为自由面，即有

当相邻部件之间发生分离时，则相邻部件界面均为自由面，在分离期间按自由面处理。

2．5 弹簧界面

由于将2个相撞部件接触面的局部变形抽象为无质量的虚拟弹簧，当应力波传播遇到弹簧元件时，弹簧变形量（ui，j－ui′，j）和撞击力Fi，j之间满足公式（2），如图5所示。

图5 弹簧界面处理Fig．5 The spring deformation model

在计算时，已知本时刻到达弹簧界面的顺波Pi－1，j－1和 逆 波Qi＋1，j－1以 及 上 一 时 刻 的 弹 簧 力Fi，j－1，本时刻的弹簧力Fi，j可由下式求得［6，7］

求得Fi，j后，离开弹簧界面的顺波Pi，j和逆波Qi，j便可利用应力波的叠加关系求出，如下

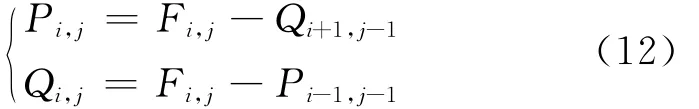
由于应力波在通过弹簧元件时，弹簧会发生压缩变形，弹簧界面两侧的速度不相等，根据式（5）可以得到

式中vi，j，vi′，j分别表示弹簧界面左右两侧的速度。

式中ui，j，ui′，j分别表示弹簧界面两侧的位移。弹簧的变形量L可表示为

2．6 工作端

到达工作端的应力波，一部分透射进工作对象使其破碎成孔；另一部分形成反射逆波，其幅值和形状取决于入射波的形状及工作对象的性质，如图6所示。工作对象力学模型采用如图2所示的弹性模型，则从工作端的反射逆波为［6］

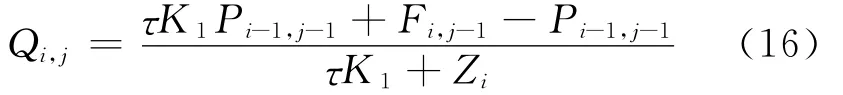
当工作端与工作介质接触时，接触界面两侧的作用力和速度分别相等，计算出反射逆波后，根据式（5）即可求出凿入力与凿入速度的大小

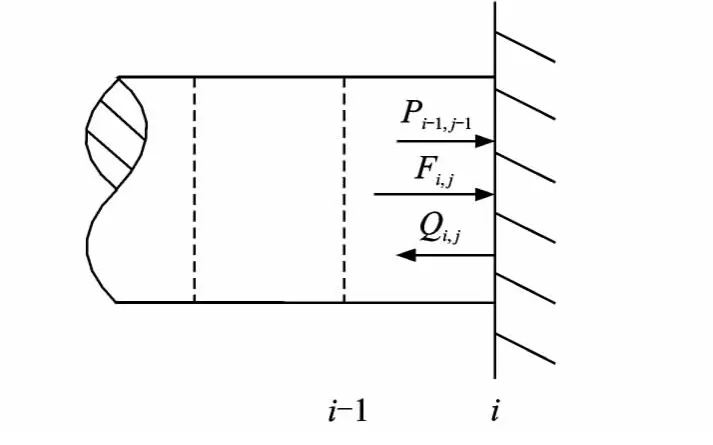
图6 应力波在工作端的传播Fig．6 Propagation of stress wave in working interface

随着钻头的凿入，凿入速度逐渐下降，最后钻头会被弹起，此时计算反射逆波时，将加载系数K1换成卸载系数K2。

2．7 界面分离处理

冲击系统中各个部件之间只能传递压应力。当出现拉应力时，原来相邻2个部件接触界面将发生分离。随着应力波在各个部件中来回传递，出现压应力时，相邻2个部件界面又将出现恢复接触的趋势。这个过程在整体上表现为部件振荡，分离界面变为自由面。由于将2个相邻部件接触面的局部变形抽象为无质量的虚拟弹簧，所以两者接触、分离、再接触过程可以根据相邻界面的位移差（也就是弹簧变形量）来判别处理。当L＞0时，表明2冲击部件接触；L＜0时表明2冲击部件分离，则此界面必须按自由面处理。

根据以上冲击系统数值计算方法，可以编制出电锤冲击系统波动力学数值模拟程序。软件程序能够实现冲击系统任一时刻的受力状态、任一点的受力历程和位移、任一冲击部件的运动状态的计算与显示和冲击系统的凿入量和效率等指标的计算。

3 电锤冲击系统波动力学模拟分析与实验验证

3．1 电锤冲击系统波动力学模型及其参数

本例中的某型号电锤冲击系统包含冲锤、冲杆及钻头三元件，冲锤在气动驱动下作往复运动撞击冲杆，冲杆产生的冲击力以应力波的形式作用于钻头，其力学模型如图7所示。

图7 电锤三元冲击系统力学模型Fig．7 The mechanics model of an electric hammer impact system involving three rods

在模型中，冲锤、冲杆及钻头的材料相同，钻头工作端硬质合金钻刃由于所占的比重很小，可以忽略其影响，因此冲锤、冲杆及钻头的力学性能参数可视为相同。其中，材料纵波波速c＝5 100m／s，材料密度ρ＝7 830kg／m3。由于工作介质为混凝土，其加载系数K1＝45MN／m，卸载系数为K2＝135 MN／m；冲锤与冲杆、冲杆与钻头撞击局部变形采用虚拟弹簧模拟，其刚度k1＝k2＝760MN／m，这些系数是通过实验获得的。冲击初速度v0＝10．5m／s，各冲击元件之间初始间隙为0。在模拟中选取时间步长τ＝0．196μs，单元长度δ＝1mm，将整个冲击系统离散成570个单元，如表1所示。

冲击系统离散之后，各界面上的截面积如表2所示。

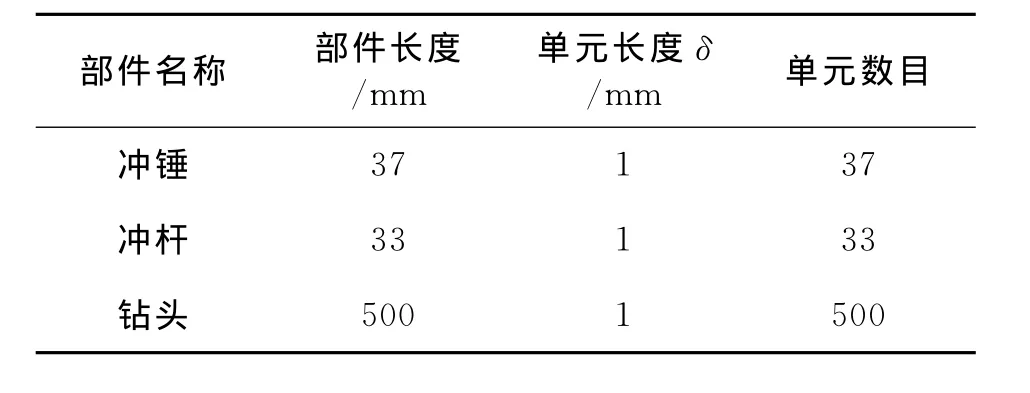
表1 电锤冲击系统离散处理Tab．1 The discrete processing of an electric hammer impact system

表2 冲击系统各单元界面的截面积Tab．2 The cross－sectional areas of element interfaces in an electric hammer impact system

3．2 电锤冲击系统数值模拟分析

通过数值模拟，电锤冲击系统部件应力幅值分布如图8所示。结果表明，冲锤中的最大压应力为281MPa，最大拉应力为19MPa；冲杆的最大压应力为281MPa，最大拉应力为21MPa；冲锤和冲杆中的应力分布总的特征是：前端压应力较大，后端出现了一定拉应力。钻头中的最大压应力为349 MPa，最大拉应力为367MPa，钻头受到的拉压应力幅值相当。

图8 电锤冲击系统应力分布Fig．8 The distribution of stress in an electric hammer impact system

为了进一步了解冲击系统各个部件中应力变化规律，分别选取图8各冲击部件中应力较大的A，B，C三处截面，其应力波历程分别如图9～11所示。

从图9和图10可以看出，冲锤撞击冲杆后，冲锤、冲杆中的应力波幅值在20μs内就由零骤增到250MPa，再经过80μs又重新下降到零附近。经过390μs后，冲杆中的应力波出现小幅增加，这是因为应力波在钻头中来回传递一次的时间是196μs。经过2个周期后，反射波中出现压应力，使钻头与冲杆又重新接触，钻头中的应力波透射到冲杆之中。经过650μs后，冲锤、冲杆中的应力波增大，这是因为冲杆在获得钻头传递过来的能量后，冲杆产生反弹，并与之前脱离接触的冲锤发生二次碰撞冲击，使冲锤、冲杆中应力波增大。从图11可以看出，钻头中出现了很大的拉应力，这是由于混凝土相对较软，混凝土没有吸收入射应力波的全部能量，能量以拉伸波的形式反射回来。

图9 冲锤上A处应力波Fig．9 The stress wave of point A in the punch hammer

图10 冲杆上B处应力波Fig．10 The stress wave of point B in the punch pole

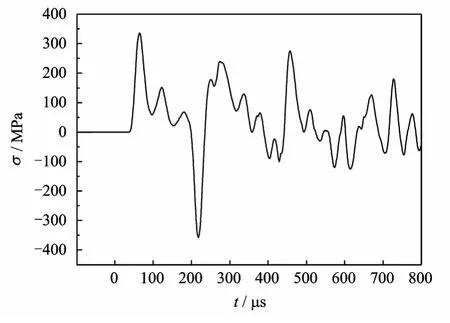
图11 钻头上C处应力波Fig．11 The stress wave of point C in the drill

综合以上分析得出如下结论：（1）在电锤冲击系统中，钻头中的应力比冲锤、冲杆中的应力大，并且承受的拉应力较大，容易促使钻头发生疲劳断裂，这可能是造成钻头寿命较冲锤、冲杆短的重要原因。（2）从各个部件应力波历程中峰值大小来看，对电锤凿入深度、效率和各个部件疲劳寿命有着决定性影响的是应力波历程中的前面1～2周期。（3）电锤这类包括3个弹性杆的三元冲击系统波动力学规律与以凿岩机为代表的二元冲击系统是基本相同的，只是冲杆、冲锤等冲击部件的回弹有着特殊性。

根据电锤冲击系统波动力学模拟分析可知：在给定条件下，该型号的电锤最大凿入力19 866N，相对应的凿深为u0＝0．441mm，效率η＝0．57。

3．3 试验验证

为了验证冲击系统波动力学建模和数值计算方法的可行性，对某型号电锤数值模拟进行实验对比分析。采用BX120－2AA应变片、Synergy动态信号采集系统组建电锤冲击测试系统，如图12所示。在本测试中，选择钻头上两个测点进行测试，冲击对象为普通混凝土试块。Synergy动态信号采集系统采用高速瞬态记录模式，采样频率设置为2MS／s，同时使用2个高速采集通道，将2个测点的采集数据并行记录到板载高速内存中，最后保存到内置硬盘中。对于测试系统记录中的电锤单次撞击期间通过2个测点的应力波波形，经MATLAB小波包进行消噪处理后，得到清晰准确的实测应力波波形。

实测的电锤钻头应力波与数值模拟结果如图13和图14所示。由图可见，在应力波历程关键的前面1～2个周期中，数值模拟结果与试验结果二者吻合较好，这表明本文提出的电锤冲击系统波动力学建模和数值模拟方法能够较好地反映冲击系统中应力波变化规律，可以运用于具体电锤的设计开发之中，减少电锤样机的试验次数，缩短开发周期，减少开发费用。模拟和实验都表明，钻头承受着与压应力相当的拉应力，这需要在电锤冲击系统设计时合理匹配各部件尺寸，尽量减少钻头拉应力，提高钻头使用寿命。

图12 电锤冲击测试系统Fig．12 The electric hammer impact test system

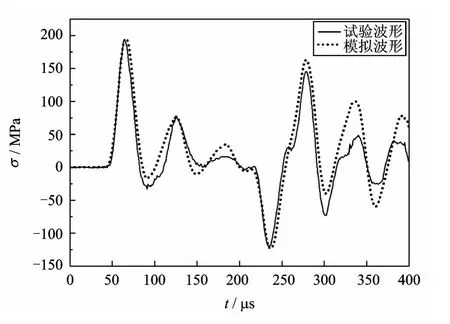
图13 钻头测点1应力波曲线Fig．13 The stress wave curve of the first point in the drill

图14 钻头测点2应力波曲线Fig．14 The stress wave curve of the second point in the drill

数值模拟结果与试验结果二者误差来源于实验测试中的随机性，采用的一维波动力学模型取代三维实体的误差和模型参数的实验辨识误差等。从时间历程来看，应力波的前半部分，也就是冲击系统的入射应力波，其波形取决于冲锤和冲杆的几何结构和力学性质。由于冲锤和杆的均匀性较好，其几何尺寸和力学性质容易精确测定，故波形的前半部分模拟结果与试验结果吻合程度较高。应力波波形出现拉应力部分是由钻头工作端反射回来的应力波决定的，因此这段波形不但与入射应力波有关，还取决于工作端工作对象的力学特性。由于数值模拟中工作对象的力学模型采用的是线弹性模型，而实际的工作对象并不是理想的线弹性模型，这样后半部分模拟结果与试验结果的吻合程度就低些。由于误差的累积效应，越往后数值模拟与试验结果误差越大。

4 结 论

（1）本文建立了以弹性杆为核心的电锤冲击系统波动力学模型。应用透反射关系法，提出了电锤冲击系统波动力学数值计算方法。以某型号电锤为例，通过电锤试验测试验证了电锤冲击系统波动力学建模和数值求解方法是正确可行的。

（2）应用电锤冲击系统数值模拟软件可获知电锤冲击系统各部件，特别是装于电锤内部不便于测试的冲锤、冲杆的应力范围、应力历程以及整个系统性能。这可以减少或者代替样机试验，降低新型电锤的开发成本和周期。

（3）模拟分析和实验表明，电锤冲击系统中钻头承受的应力比冲锤、冲杆中的应力大，特别是承受了较大的拉应力，这是引发钻头疲劳断裂，造成钻头寿命较冲锤、冲杆短的重要原因，在设计中应该引起足够重视。

［1］ Xu L．Finite element analysis of the impact process of concrete drilling［J］．Int．J．Computer Applications in Technology，2005，24（1）：1—16．

［2］ Luciaano E Chiang，Dante A Elias．A 3DFEM methodology for simulating the impact in rock－drilling hammers［J］．International Journal of Rock Mechanics and Mining Sciences，2008，45：701—711．

［3］ Hustrulid W A，Fairhurst C．A theoretical and experimental study ofthe percussive drilling of rock PartⅠ－Ⅳ［J］．Int．J．Rock Mech．Mining Sci ＆ Geo．Abstract．1971，8：311－333，335－356．1972，9：417—429，431—449．

［4］ Lundberg B．Energy transfer in percussive rock destruction—Ⅰ－Ⅱ：comparison of percussive methods［J］．Int．J．Rock Mech．Min．Sci．＆Geo．Abstract，1973，10（5）：381—399，401—419．

［5］ 刘德顺，李夕兵，朱萍玉．冲击机械动力学与反演设计［M］．北京：科学出版社，2007．

Liu deshun，Li xibing，Zhu pingyu．Dynamics and Inverse Design of Impact Machines［M］．Beijing：Science Press，2007．

［6］ 徐小荷．撞击凿入系统的数值计算方法［J］．岩石力学与工程学报，1983，3（1）：75—83．

Xu Xiaohe．The digital calculation method of striking penetration system［J］．Chinese Journal of Rock Mechanics and Engineering，1983，3（1）：75—83．

［7］ 邹定详．杆件纵向撞击面局部变形的非线性模型［J］．东北大学学报，1980，01：121—129．

Zou Dingxiang．A nonlinear theoretical model of the partial deformation on longitudinally striken surface bars［J］．Journal of Northeastern University，1980，01：121—129．

［8］ 刘德顺，何先可，段凯，等．基于入、反射波的杆波阻特性反演方法［J］．煤炭学报，2009，34（9）：1 281—1 284．

Liu Deshun，He Xianke，Duan Kai，et al．The inversion of variable characteristics impedance of the rod basedon incident waves and reflection waves［J］．Journal of China Coal Society，2009，34（9）：1 281—1 284．

［9］ 刘德顺，何先可，段凯．基于特征线的杆波阻特性两点应变法反演研究［J］．振动与冲击，2011，30（2）：69—72．

Liu Deshun，He Xianke，Duan Kai．Inversion of characteristic impedance of a drill bit using two－point Strain measurement based on characteristic lines［J］．Journal of Vibration and Shock，2011，30（2）：69—72．