换刀机构圆弧分度复合凸轮三维建模*

2013-09-12邹运，王盟

组合机床与自动化加工技术 2013年8期

邹运，王盟

(大连高金数控集团有限责任公司，辽宁大连 116620)

1 弧面凸轮运动规律与方程

采用机械式的复合凸轮机构代替电子控制，是提高系统可靠性的有效方法。复合凸轮实际上是通过两套凸轮机构组合在一起来实现动作的耦合，换刀系统的复合凸轮是由实现机械手旋转动作的分度凸轮和实现机械手插刀、拔刀到动作的槽式凸轮组合而成。

自动换刀系统机械手的换刀动作顺序是在初始位置顺时针旋转60度，此时机械手一端抓住主轴上的旧刀具一端抓住运刀轨道上的新刀具，机械手拔刀165mm，逆时针旋转180度，插刀165mm，把旧刀具放到运刀轨道上，新刀具插在主轴上，顺时针旋转60度，停在了原来初始位置，换刀机构和复合凸轮实物如图1，图2所示。

图1 换刀机构

图2 复合凸轮

机械手的旋转是通过复合凸轮的分度轮及锥齿轮旋转实现的;机械手的插刀、拔刀直线位移动作是通过复合凸轮的沟槽凸轮及其连接的摆杆摆动实现的。工程图纸上复合凸轮配合轨迹的要求如图3所示。

图3 凸轮运动曲线

图3中上边这条曲线是摆杆直线输出位移，下边这条曲线是分度轮旋转角度输出，横坐标是复合凸轮的电机驱动的转动输入角度。图中标识“MS”为改进正弦修正，“CW”为顺时针旋转，“CCW”为逆时针旋转。由图中可以看出在摆杆移动过程和分度轮旋转过程都是用改进正弦修正，在输出值变化的曲线段两端的1/8处是分界点，其整个加速度曲线用三段三角函数曲线代替，这样的曲线的优点是加速度值较小而且整个域内连续，把图3中初始值和终值及表1中的各个几何参数带入改进正弦加速度运动规律，可得出复合凸轮输出运动方程如下。

摆杆输出端的运动方程S(φ(t))：

分度轮转角输出端的运动方程Φ(φ(t))：

参数说明：h—从动件行程;β—凸轮行程角;φ—凸轮转角;s(φ)—从动件位移;v(φ)—从动件速度;a(φ)—从动件加速度。

2 凸轮三维建模

采用solidwork复杂曲面建模技术建立弧面分度凸轮机构的基本几何参数如表1所示。

表1 复杂曲面弧面分度凸轮机构基本几何参数

弧面分度凸轮的毛坯是通过凸轮的顶弧面半径画弧，然后利绕中心线旋转生成。具体命令是首先草图绘制，画出凸轮截面边界轮廓，然后利用特征工具栏中的旋转凸台/基体命令绕中心线旋转草图360°得到弧面分度凸轮基体的毛坯，然后在凸轮底面新建草图，画出凸轮所在凸轮的轮廓圆后，使用特征工具栏中的拉伸凸台/基体命令生成凸轮所在的凸台，最终得到弧面分度凸轮的毛坯模型，以下的操作命令均在该毛坯上执行。在SOLIDWORKS中绘制3D草图，利用插入→草图绘制的实体→方程式驱动的曲线命令在凸轮毛坯上建立啮合的滚子的理论廓面曲线如图5所示。

图4 弧面分度凸轮的毛坯模型

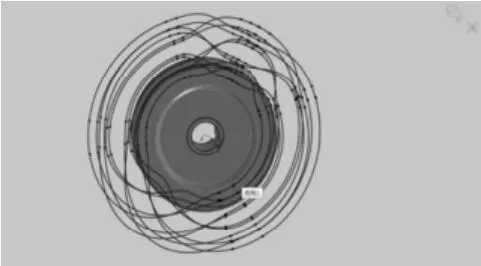
图5 分度盘弧面曲线

空间复合凸轮自动换刀装置中弧面分度凸轮的运动可以分为起始段，分度1段，停歇1段，分度2段，停歇2段，分度3段和结束段，各段行程如表2所示。

表2 各段行程

对同一个滚子来说，最低点K1和最高点K2的轨迹曲线相互平行，所有滚子的轨迹曲线组成封闭的3对互相平行的6条封闭曲线。下面以滚子1的K1点为例说明其轨迹曲线建模过程，其方程如表3所示。

表3 曲线方程

(续表)

同理，令r=45，可以得到滚子1的K2点的理论轨迹曲线。应该注意的是，SOLIDWORKS中的对于角度的单位默认为弧度，因此凸轮和分度盘的转角等单位应该先化为弧度之后再代入，同时，建立曲线的时候应该注意坐标系的建立是否正确，弧面分度凸轮的旋转轴应该是Z轴，否则建立的曲线会产生很大偏差。分度盘所有滚子的理论滚子绘制出来之后，应用插入→曲面→边界曲面命令，将不同半径相互平行的轨迹曲线扫描生成空间曲面，即为弧面分度凸轮的理论廓面曲面。生成理论轮廓曲面之后，使用SOLIDWORKS中插入→切除→加厚命令对凸轮毛坯进行实体切除，理论廓面曲面的法向偏置距离为分度盘滚子的半径15mm，即得到了弧面分度凸轮的精确轮毂曲面模型，生成的复杂曲面弧面分度凸轮如图6所示。