刀库及自动换刀装置可靠性熵法评定技术*

金渊源，冯虎田

(南京理工大学机械工程学院，南京 210094)

0 前言

链式刀库及机械手属于典型高可靠性要求的大型复杂系统，其系统组成主要是不同指数型单元组成的复杂串联系统。在进行可靠性研究时，以大型加工中心为样本进行多台、多次可靠性现场试验耗资巨大、周期太长，是极其不现实的，甚至在子系统级别的可靠性试验也不能像电子元器件一样进行大批量的综合试验。因此很难获取足够的现场试验数据和故障样本，此时进行系统的可靠性综合评估是非常困难的。本文在总结分析传统可靠性评估方法的基础上，利用信息论中的相关理论对不同环境下的试验信息进行折合，利用复杂系统各子系统、各零部件的试验数据进行折算分析，以金字塔模型［1］为基础进行复杂系统可靠性综合评定。

1 传统方法局限性

传统方法的可靠性评估方法主要以概率统计相关理论为基础的，主要包括经典方法、Bayes方法和Fiducial方法。在过去50多年的可靠性综合评估技术方面，这些理论有着非常重要的作用，但是，随着研究对象日益复杂，可靠性试验的数据样本信息明显减少。基于传统方法的可靠性评估技术在数据处理与分析方面有着明显的缺陷与不足。

(1)经典方法，常见的有MML法、SR法、L-M法等。主要是以点估计不变为原则，对试验数据进行压缩处理，虽然计算简单，但损失大量的有用信息，应用在大型复杂系统当中，由于试验信息的多次压缩和信息缺失的逐层累加使得整机系统的可靠性评估过于保守。

(2)Bayes方法和Fiducial方法，理论出发点是“有界随即变量的分布函数由各阶矩的无穷序列唯一确定”，即令系统的近似分布和精确分布拥有尽可能多的矩相等来进行分布拟合与数据处理［2］。这种方法将主观信息作为先验信息，然后进行推理论证，用样本信息修正先验信息，然后进行统计推断，是解决小样本推断的有效方法之一，其关键点是构造包含丰富主观信息的先验分布。但是，目前的科研实践中，验前分布不易选取，并且在数据处理方面仅利用可靠性的两阶矩，部分信息缺失。并且由于其数学计算太过复杂，可靠性特征量逐层递减的特点，应用在单元系统复杂的可靠性评估存在缺陷。Fiducial方法经过多年摸索，不宜进行大型系统的可靠性评定。

(3)理论分析与科学试验方法可以从材料特质、失效机理与零部件磨损等方面预计复杂产品的行为结果和故障模式，从而得到产品的一些基本可靠性信息，这些信息常常来自于专家经验，是通过实践的积累得到的基于实际使用状况的人类大脑对客观规律的主观反映，此类方法仅能从部分方面对可靠性进行评估，结果往往依赖于多年的实际工作经验。

2 基于信息论试验信息折算

对系统可靠性的数据分析，如果像单元一样，根据系统的试验数据来进行统计推断，在工程上存在很大困难，甚至不可能。因此，在进行系统可靠评定时，常以“金字塔”模型为基础，充分利用系统以下各级的可靠性数据，缩短试验周期，以较少的系统运行数进行可靠性综合评定。

对于机电一体化的复杂系统，应根据系统的现场试验数据，将单元的试验数据折算成系统的指数型(成败型)等效数据，并将此数据与真实试验数据进行综合，得到系统的综合信息，以此为数据基础，根据指数型评定方法求出系统可靠性的特征量近似限［3-5］。

(1)不同环境下单元试验信息折合

对于单一因素的环境试验，在实验室中可方便的进行模拟，但若产品在综合环境下进行工作，在实验室试验总很难完全模拟实际工况，故采用现场数据统计计算得出环境因子，并进行可靠性试验单元信息折合。

设某种产品寿命服从指数分布，在环境A下对环境B的环境因子为K，若在环境A，B下分别进行定数截尾试验，记为(zi，τi)，i=A，B;zi表示在环境 i下的失效次数，τi表示系统在环境i下的现场试验时间。

因此，可以知道环境因子K置信度为γ的置信上限为：

在数据处理当中，若要将环境A下的试验信息折合到环境B当中，需利用环境因子K的置信上限，即：(ZB，τB)→(ZA，τA/K)，在与环境 A 下的试验信息相综合即可得到最后的折算数据：

(2)不同指数型单元试验信息折合

设系统由m(m≥2)个相互独立的指数型单元组成，已知第j(j=1，2，…，m)个单元的指数型数据为(zj，ηj)，zj为第 j个单元的实际失效次数，ηj为第 j个单元的等效任务次数，任务时间为t0j，总试验时间为τj，失效率为λj，根据指数分布的无记忆性，第 j个单元在每个等效任务数内就具有相等的可靠度Rj和不可靠度Fj(Fj=1－Rj)。第j个单元在总体试验时间τj内应该提供的信息量为：

组成系统m个不同指数型单元在全部试验时间内所提供总信息量为：

如果将Rj、Fj取其极大似然估计 MLE、，带入公式当中，可以得到不同指数型单元组成指数型系统时单元试验信息商法折合的通用公式：

Rt0即为系统完成一次任务时的成功概率P，则公式又可以表示为：

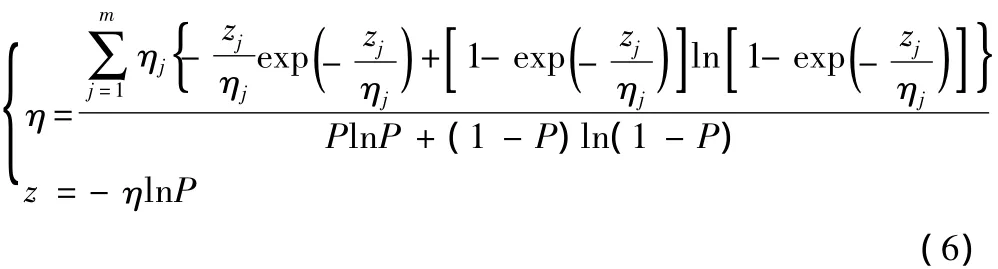
3 串联系统可靠性熵法评定近似限

迄今为止，由于试验向量的排序仍然存在困难，不便应用于实际工程中，且求解精确解的方法在计算上也过于复杂，因此求解近似解较有实际意义。国内外经过多年研究，在针对串联系统模型的可靠度近似下限方面，主要有经典方法与Bayes方法两种［6－7］。下面针对本文的信息熵理论，在参考国内外可靠度近似评定技术的基础上，采用经典方法，得到针对指数型单元系统的可靠性第二近似限。记为。若系统由熵法折合的等效试验数据为(失效次数，任务数)=(Z，η)，系统实际试验数据为(失效次数，任务数)=(Z'，η')，则可以得到：

单元可靠性平等方法中失效率非随机化最优置信计算公式有：

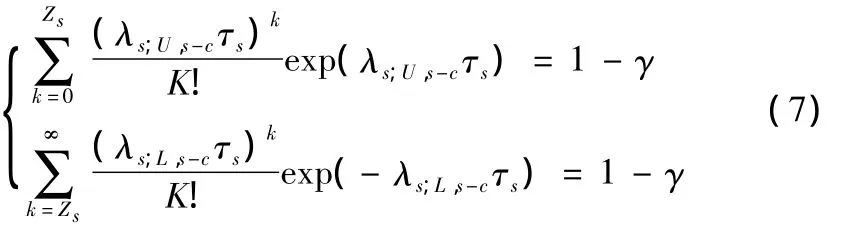
若以λs;U，s－c表示系统失效了的非随机化最优置信上限，t表示系统的任务时间表示自由度为2Zs+2的χ2分布的γ分位数，则可以得到基于经典法的系统可靠度第二近似限为：

表1 链式刀库及机械手厂级数据及实验室数据统计表

图1 链式刀库及机械手金字塔分级结构图

4 工程应用

针对本文研究对象大连高金链式刀库及机械手系统，进行“金字塔”分级时可简化分为三级：整机级、分系统级、部件级。当然根据具体情况，如需更准确的数据评定，可向下再细分为零件级。链式刀库及机械手系统各分系统级寿命表现形式基本类似，均可近似认定为指数分布类型。设链式刀库及机械手整机的指数分布特征量用(Z，τ)表示，分系统级的指数分布特征量可以用(Zn，τn)来表示，部件级的指数分布特征量用(Znx，τnx)来表示。图1给出了链式刀库及机械手系统金字塔型分级。表1给出了链式刀库及机械手厂级数据及实验室数据。

(1)下面以换刀机械手为例进行环境信息折合计算。

设换刀机械手每次换刀时间为1分钟，将生产厂商试验数据折合成实验室现场实验数据，则可知：

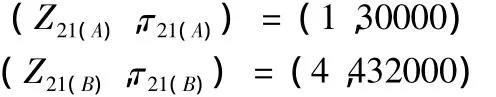
若置信度取为0.9。则可计算环境因子K。

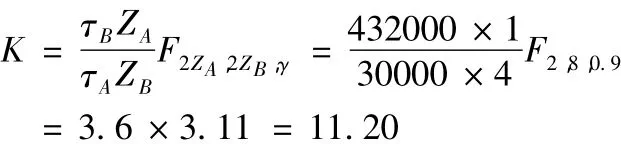
由此可以进行信息折合，得到：

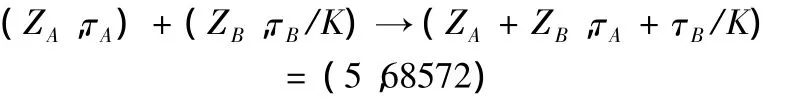
(2)其他部件试验数据进行同样处理，可得到基于生产厂商和实验室试验数据的可靠性折合数据，再以此为基础，进行部件试验信息折合。

设各部件在等效任务数内失效数(τi，ηi)则有：

① 储刀配套装置部件(Z11，τ11)=(1，30000);

② 链条传动装置(Z12，τ12)=(0，30000);

③ 交流伺服电机(Z13，τ13)=(4，37300);

④ 推刀、锁刀装置(Z14，τ14)=(2，33334);

⑤ 换刀机械手(Z21，τ21)=(5，68572);

⑥ 凸轮传动装置(Z22，τ22)=(5，68572);

⑦ 三相异步电机(Z23，τ23)=(2，30000);

⑧ 气压配套系统(Z31，τ31)=(1，30000);

⑨ 数控系统(Z32，τ32)=(4，30000);

⑩ 检测装置(Z33，τ33)=(1，30000)。

将这些部件的可靠性特征量带入公式5、公式6中计算，则可以得到其部件级试验信息折合。计算可得：

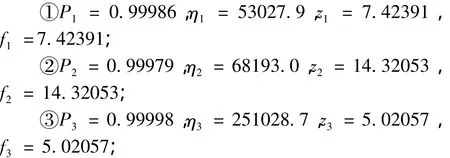
同样，应用信息熵折合原理，分系统的指数分布特征量折合为系统级可靠性分布特征量，即可得到链式刀库及机械手的可靠性特征量。

刀库分系统为(Z1，τ1)=(7.42391，53027.9);机械手分系统为(Z2，τ2)=(14.32053，68193.0)，控制装置分系统为(Z3，τ3)=(5.02057，251028.7)，代入公式5、公式6中计算可得：

P=0.99963，η =81440.56652，z=30.13301，f=30.13301

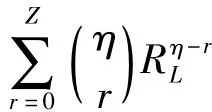
查χ2分布分位数表并经线性差值计算可得如下计算结果：

因此得出置信度为0.8与0.9时的系统可靠度第二近似下限。

5 结论

本文利用信息论中的相关知识，对不同试验环境下的现场试验信息进行数据折合，并研究了针对可用“金字塔”模型分级的复杂机电产品系统、分系统、零部件之间试验数据的信息折算问题。解决了使用传统方法对复杂机电产品进行可靠性评定时试验样本少、试验周期长、真实试验数据信息量不足等问题。在大型数控机床可靠性评定方面具有广泛应用价值。

［1］冯虎田.火箭导弹发射系统可靠性研究［D］.南京：南京理工大学，2000.

［2］李总根.大型复杂系统可靠性综合的信息熵方法［J］.中国安全生产科学技术，2008(3)：54－58.

［3］Easterling R.G.Approximate confidence limits for system reliability.JASA，1972：220 －222.

［4］Preston P.F.Confidence limits for system reliability，ADA047533，1976.

［5］王振邦.成败型系统可靠性综合评定的H-熵法［J］.系统工程与电子技术，1989(8)：66－81.

［6］施军.系统可靠性评定的熵(法)近似限［J］.航空学报，1996，17(5)：543 －548.

［7］孙有朝，等.发动机可靠性多级综合的信息熵法第一近似限［J］.航空动力学报，2002，17(4)：412－415.

［8］施军，邓克绪，段文颖.k/N(G)系统可靠性评定的熵(法)近似限［J］.航空学报，1998，19(1)：30－34.