机车发动机用凸轮轴磨削新工艺*
2013-09-12王歆令沈南燕何永义
王歆令,李 静,沈南燕,何永义
(1.上海市机械自动化及机器人重点实验室,上海 200072;2.上海大学机电工程与自动化学院,上海 200072)
0 引言
凸轮轴是机车发动机关键零部件之一,主要的作用是控制机车气门的开启和闭合,与发动机的功率、扭矩输出以及运转的平顺性有很直接的关系,因此凸轮轴加工质量的高低很大程度上影响着发动机性能的优劣。
机车发动机用凸轮轴具有重量大、体积大、型线复杂、多相位等特点,特别是部分轮廓可能因为性能或控制需求设计为凹弧线(该段型线曲率为负),在实际加工中会引起砂轮干涉及表面烧伤等问题,大大增加了加工难度。因此,通常采用半径较小的砂轮进行整周磨削的传统工艺,但是加工的效率和精度均受到影响。为了实现机车发动机用凸轮轴的高效高精度加工,与上海机床厂有限公司合作共同开发MK8340/1500凸轮轴数控切点跟踪磨床。本文将从凸轮随动磨削机理及运动模型出发,结合机车发动机用凸轮轴的几何特征,详细分析了带有凹弧线段凸轮轴的加工难点,提出凸轮凹弧段轮廓重构方法及大小砂轮配合磨削新工艺。
1 凸轮凹弧段加工难点
1.1 机车发动机用凸轮轴描述
本文加工对象是两根长度不一的机车发动机用凸轮轴,长轴型号为青岛淄柴博洋8N330,长度为901.5mm、基圆半径为70mm;短轴型号为青岛淄柴博洋6N330,长度为459.4mm、基圆半径为73mm。每根凸轮轴上均按顺序配有进气凸轮、排气凸轮以及油泵凸轮。长短轴上各凸轮凹弧段轮廓对应角度范围及该范围内最小曲率半径如表1所示。

表1 长短轴各凸轮内凹型线轮廓对应角度范围及该范围内最小曲率半径
由表1可知,长轴上的油泵凸轮与短轴上三片凸轮均存在凸弧段和凹弧段。
1.2 运动干涉
本文凸轮轴加工采用切点跟踪磨削法,它通过数控磨床头架驱动工件旋转,砂轮架根据头架位置随动跟踪进行磨削。现以短轴上油泵凸轮为例,根据切点跟踪磨削运动模型[1-2],在头架匀角速度旋转的情况下,分别求出使用大小砂轮加工时砂轮中心的位移X。凸轮转角在[0°,360°]区间上取等间隔的3601 个点 αi(i=1,2,…,3601),求出各点对应砂轮中心位移Xi(i=1,2,…,3601)后,将相邻两个凸轮转角点对应的砂轮中心位移相减,得到一组差值,仿真结果如图1和图2所示。

图1 大砂轮加工时砂轮中心位移差值曲线
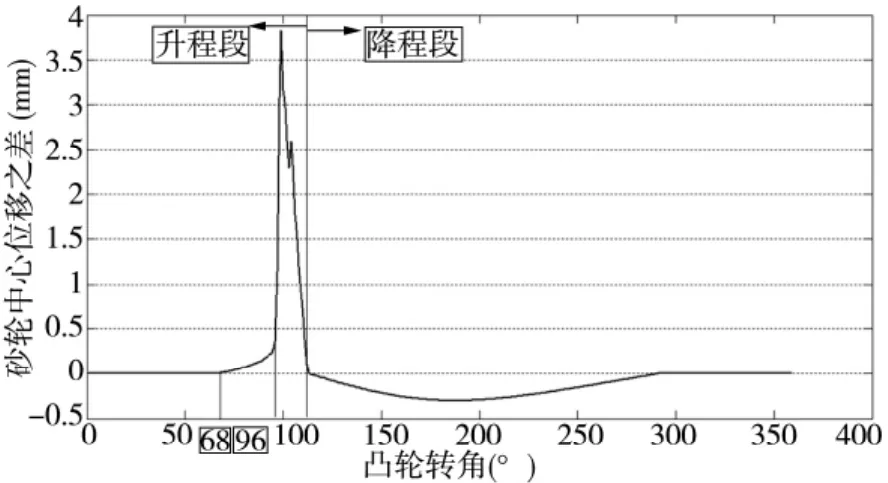
图2 小砂轮加工时砂轮中心位移差值曲线
比较图1和图2可知,小砂轮磨削油泵凸轮升程段期间,相邻两点砂轮中心位移差值始终为正,表示砂轮架始终向远离凸轮的方向运动,符合切点跟踪磨削规律,而大砂轮磨削油泵凸轮升程段期间,在凸轮转角为68°~96°时(油泵凸轮凹弧段轮廓处),相邻两点砂轮中心位移差值为负,表示砂轮架突然出现向靠近凸轮方向运动的状况,此时砂轮将与油泵凸轮发生干涉。因此,无法利用大砂轮按照切点跟踪磨削方法完成该凹弧段轮廓的加工。
1.3 表面烧伤
在实际磨削加工中,针对凸轮这类非圆零件而言,其各磨削点的接触弧长不尽相同。式(1)是凸轮磨削时砂轮与工件的运动接触弧长公式[3-4]:

其中,L为磨削点的运动接触弧长,Rs为砂轮半径,vw为工件的速度,vs为砂轮的线速度,ap为磨削深度。ρ为磨削点的曲率半径,当ρ>0时为凹弧段的曲率半径,ρ<0时为凸弧段的曲率半径。
假设ρ>RS,由式(1)可得,在磨削点位置相同且砂轮线速度及磨削深度一定的情况下,与磨削凸弧段时相比,磨削凹弧段时的运动接触弧长较长。若凹弧段上磨削点曲率半径与砂轮半径越接近,则运动接触弧长越长。因此使用大砂轮磨削凸轮凹弧段时,接触区域增大,砂轮与凸轮凹弧段之间空隙减小,冷却液不易流入,热量不易散发,局部温升过高,最终将导致凸轮表面烧伤。
1.4 效率与精度
虽然使用小砂轮磨削带有凹弧段的凸轮可以避免运动干涉,但是其运动接触长度较小,进给量小,导致磨削时间长,加工效率低。此外,小砂轮为了达到较高的线速度,转速需要提高,因此,加速了砂轮的磨损,长时间大进给量磨削时加工精度无法保证。
2 凸轮轴磨削新工艺
2.1 大小砂轮配合磨削新工艺
在磨削加工带有凹弧段的凸轮时,单独使用大砂轮可能带来运动干涉和表面烧伤问题,而单独使用小砂轮则会对加工效率和精度产生影响。为了避免这些问题,本文提出大小砂轮配合磨削的新工艺,即加工前期使用大砂轮进行粗磨和半粗磨,当运动到凸轮凹弧段时按照新的轨迹走刀,避开该凹弧段,将大部分工件余量磨完之后使用小砂轮进行凸轮整周的精磨和光磨,期间磨完未加工的凹弧段。该工艺充分利用了大小砂轮磨削的优点,可同时保证加工精度和效率。
凸轮凹弧段轮廓重构是该磨削工艺实施的重点,既要保证砂轮走刀过程中不磨削到凸轮凹弧段,又要使砂轮进给过程中尽可能平稳,无振动冲击。
2.2 凸轮凹弧段轮廓重构方法
为了充分利用大砂轮磨削的优点,将凸轮凹弧段轮廓重新构建成凸弧,然后根据新的轮廓给出一组新的升程值,并求得新的加工轨迹,使得大砂轮磨削加工时避开凹弧区域。如图3所示,首先在凸轮轮廓上选取A、B两个点以确定重构的范围,选取的两点要满足以下三点要求:
(1)轮廓上两点A、B所圈定的区域必须包含凸轮完整的凹弧线段;
(2)为保证重构以后凹弧段向外凸,要求A、B两点的切线交点在凸轮轮廓外;
(3)A、B两点切线形成的夹角应尽可能接近180°,使砂轮运动轨迹长度缩小。

图3 凸轮凹弧段轮廓重构示意图
构建曲线的数学表达式常采用多项式,其特点是运算速度快、曲线形状易于控制,适合于工程运用。若多项式的阶数过低,则很难保证曲线在连接点上的连续性,然而采用过高阶数的多项式,则很难控制曲线的形状。因此,本文采用三次多项式进行凹弧段轮廓重构,既能保证曲线在连接点上的连续性又能容易使曲线保持外凸的形状。
2.2.1 基于三次多项式的凸轮凹弧段轮廓重构
为了实现重新构建的凸弧段与其余凸轮轮廓段在连接点A、B上连续且光滑过渡,就需要满足两段曲线在连接点处的坐标及一阶导数均相同。由一般数学知识可知,一个三次多项式根据这四个条件可确定。三次多项式方程如公式(2)所示:

首先根据提供的凸轮角度升程值表,推出凸轮轮廓点的极坐标(θi,ρi),然后将这些点转换成直角坐标(xi,yi),并进行三次样条曲线拟合,求出连接点A、B的斜率kA,kB,将其代入如下公式即可求出三次多项式的系数:
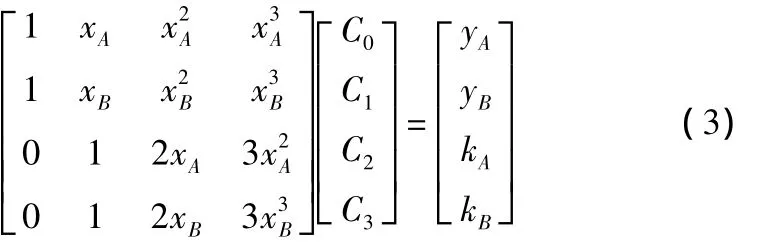
最后根据三次多项式可求得新的凸轮轮廓和升程值[5-6],进而求出新的大砂轮加工轨迹。以短轴油泵凸轮为例,其重构范围为58°~102°,重构前后的凹弧段轮廓如图4所示。
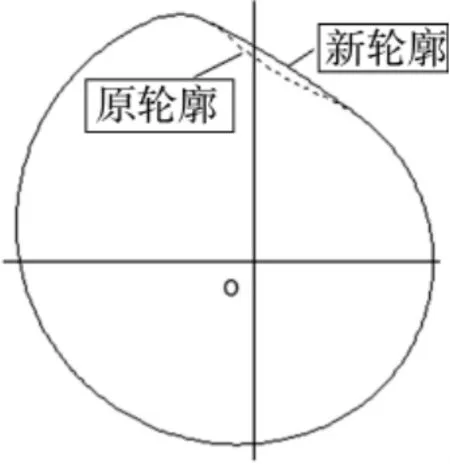
图4 重构前后的凸轮凹弧段轮廓
2.2.2 凸轮重构段砂轮架速度优化
凸轮轮廓的改变将直接影响头架的速度和加速度,从而导致砂轮架的速度和加速度也发生变化。本文在恒线速度规律控制下进行仿真,基圆转速为10r/min,根据切点跟踪磨削运动模型[1]以及短轴油泵凸轮升程值,计算得到头架转速和砂轮架的位移,并分别对其进行求导处理后最终得到砂轮架进给速度、加速度和头架的加速度。图5和图6为头架的转速、加速度曲线,图7和图8分别为砂轮架的速度、加速度曲线。
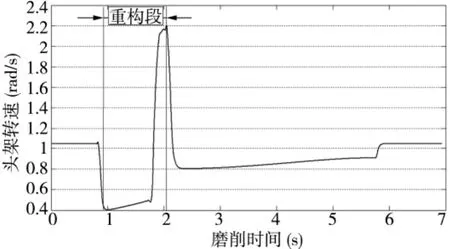
图5 头架转速曲线
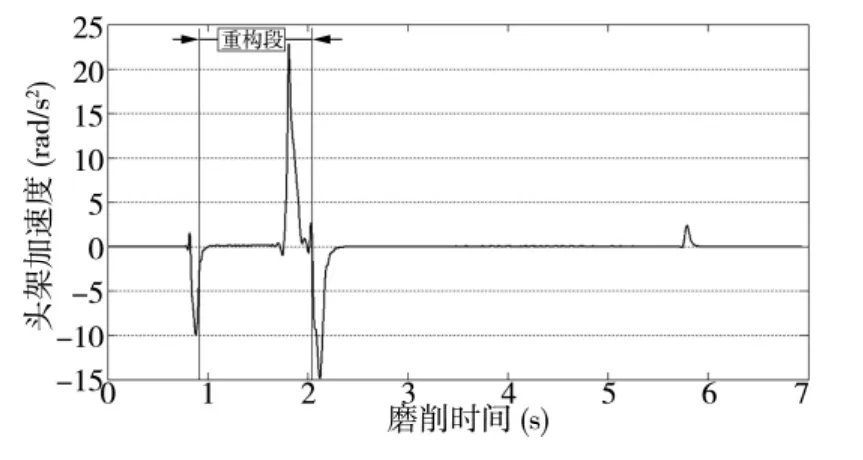
图6 头架加速度曲线


图7 砂轮架进给速度曲线
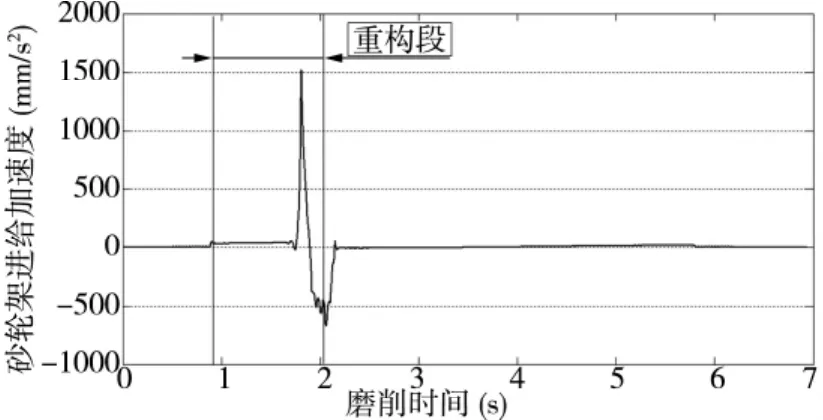
图8 砂轮架进给加速度曲线
从图中可以看出,在重构范围内的砂轮架进给加速度最大可达到1520mm/s2。由于机车用凸轮轴体积和重量都较大,因此在实际磨削中,受到机床伺服系统性能和本身惯性的制约,砂轮架加速度过大会使得X轴有较大的滞后,跟踪误差变大,同时产生机床振动,影响凸轮磨削表面质量。由此可见,利用三次多项式进行凸轮凹弧段轮廓重构可能会影响砂轮架的运动性能。
由于在凸轮重构段头架与砂轮架的速度变化趋势一致,本文提出通过降低头架的加速度,减小砂轮架加速度,以此优化砂轮架速度的方法。具体实施过程为:在凸轮重构范围内,确定头架转速曲线上与砂轮架过大加速度相对应的区域,构造三次多项式曲线替代原有区域上的转速曲线,首尾连接点要求连续且平滑过渡,新的转速曲线趋势要求更为平缓,可达到降低该段头架加速度的目的。
图9为局部优化前后的头架转速曲线,图10和图11分别为局部优化后的头架加速度、砂轮架进给加速度曲线。由图可知,头架在重构段上的加速度减小,砂轮架的进给加速度也从原来的1520mm/s2降到了654mm/s2。因此,从仿真结果看出该方法能达到降低该段砂轮架加速度的目的。

图9 局部优化前后的头架转速曲线
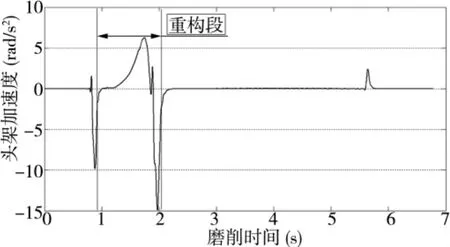
图10 头架加速度曲线
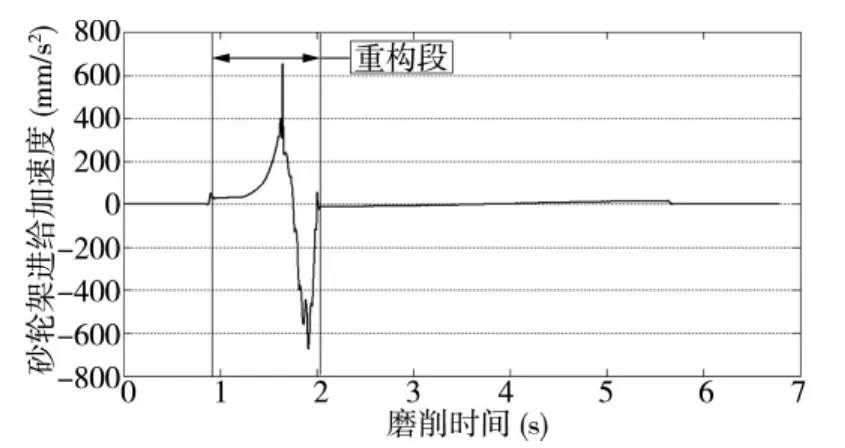
图11 砂轮架进给加速度曲线
3 凸轮轴磨削新工艺实验
凸轮轴磨削新工艺实验在与上海机床厂有限公司合作共同开发MK8340/1500凸轮轴数控切点跟踪磨床上进行,该机床配有发那科310i-MODEL A数控系统,采用双砂轮回转结构,通过发那科高速磨削循环和进给叠加实现凸轮轴的磨削加工,图12为凸轮加工实验环境。
实验对象为短凸轮轴上的油泵凸轮,主要工艺参数如下:基圆半径r=73mm、大砂轮半径RBS=175mm、小砂轮半径 RSS=95mm、砂轮线速度 ν=80m/s、基圆转速 n=10r/min、粗磨进给量 a1=20μm/r、半粗磨进给量2、精磨进给量 a3=5μm/r,磨削过程采用恒线速规律控制。

图12 凸轮加工实验环境
磨削加工后通过ADCOLE检测仪检测出的凸轮升程误差曲线如图13所示,凸轮升程最大误差为-0.024mm,凹弧段最大误差为-0.011mm。相比传统磨削工艺,在保证相同精度的条件下提高了加工效率。
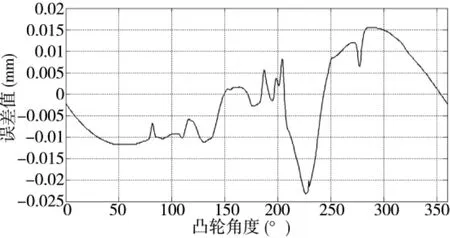
图13 凸轮升程误差曲线
4 结语
实验结果表明本文提出的机车发动机用凸轮轴磨削新工艺具有一定的实用性和可行性,磨削过程中所采用的轮廓重构方法以及砂轮架速度优化方案能够满足凸轮磨削加工的精度和效率要求,为凸轮轴高速磨削提供了一种新方法。
[1]肖真健.数控磨床磨削凸轮轴类零件的数学模型与试验研究[D].湖南:湖南大学,2001.
[2]许第洪.切点跟踪磨削法核心技术的研究[D].湖南:湖南大学,2005.
[3]李静,何永义,沈南燕,等.大功率船用柴油机凸轮的恒磨削量磨削新策略[J].机床与液压,2008,36(5):301 -303.
[4]李伯民,赵波.现代磨削技术[M].北京:机械工业出版社,2003.
[5]刘善林,胡鹏浩,王会生.基于SolidWorks二次开发的凸轮廓线精确设计及运动仿真[J].机械传动,2008,32(5):46-48.
[6]方芳.基于SolidWorks的平面凸轮设计系统研究[D].成都:西南交通大学,2010.
[7]李人厚,张平安.精通Matlab 5[M].西安:西安交通大学出版社,2001.
[8]盛晓敏,宓海青,陈涛,等.汽车凸轮轴的高速精密磨削加工关键技术[J].新技术新工艺,2006(8):61-64.
[9]李勇,段正澄,胡伦骥.数控凸轮轴磨削指令曲线的优化[J].制造业自动化,2006,28(6):47 -50.
[10]Rowe,W.Brian.Principles of Modern Grinding Technology[M].William Andrew,2009.
