数控加工中非圆曲线轮廓的三圆弧逼近方法
2013-09-12金艳玲杨东武姚东成
金艳玲,杨东武,姚东成
(1.中航工业西安飞行自动控制研究所,西安 710065;2.西安电子科技大学机电工程学院,西安710071)
0 引言
目前,一般的数控机床只具备直线插补和圆弧插补功能。当加工由双曲线、椭圆、摆线等非圆曲线组成的平面轮廓时,就得用若干直线段或圆弧段去逼近其轮廓,并计算出逼近线段与非圆曲线的交点或切点,即插补节点。采用直线段逼近非圆曲线,一般数学处理较简单,但节点计算时的坐标数据较多,且由于各节点连接处存在尖角,刀具在尖角处不能连续对零件进行切削,导致零件表面出现硬点或刀痕,从而降低加工表面质量。采用圆弧段逼近非圆曲线,不仅可大大减少程序段的数目,而且当采用彼此相切的圆弧段来逼近非圆曲线时,能够使工件表面整体光滑,有利于加工表面质量的提高。
用圆弧逼近数控加工曲线的方法分为两大类,即细分曲线(即离散点列或列表曲线)的插值或拟合[1-2]以及自由型曲线的拟合[3-5]。自由型曲线拟合方法是在已知零件轮廓曲线方程时较常采用的插补方法,具有误差控制精准的优点。本文讨论自由型曲线的拟合方法。
曲率圆法是对自由型曲线拟合的基本方法,有时也被称为等误差圆弧逼近法,其原理是通过控制所生成的插补圆弧段与实际工件轮廓曲线均位于曲率圆与偏差圆之间,以使圆弧插补的逼近误差总小于或等于插补容差。相比与其它圆弧插补方法,它具有编程时算法设计简单,误差控制直接的优点,成为数控编程类教材中圆弧插补的基本方法[6]。采用彼此相切的圆弧段来逼近非圆曲线时,能够使工件表面整体光滑,加工质量较高。文献[3-4]中的整体最优双圆弧逼近方法计算参数多,计算量大,程序设计复杂。文献[7-9]中变步长双圆弧逼近方法的误差控制采用后验方式,即先构造圆弧后通过在插补区间取点的方式检验误差,通过误差检验结果实时调整步长并重新生成圆弧;方法中的步长调整没有规律可循,导致每个插补区间的圆弧生成与误差检验可能会多次反复,数据处理过程的计算量较大。
借鉴曲率圆法中的误差控制原理,本文给出非圆曲线轮廓的一种三圆弧逼近方法。在介绍方法基本思想的基础上,给出圆弧插补节点及圆弧参数的计算步骤,并进行方法的可行性分析。
1 三圆弧逼近方法
1.1 圆弧插补节点的计算
设平面轮廓曲线具有显式表达式,且加工时的插补容差为δa>0。在曲率极值点、拐点以及曲率非连续点处将整个轮廓曲线划分为多段,这样,每一局部段就是曲率单调的。不妨设某一段曲线)AP的曲率是单调下降的,如图1所示。
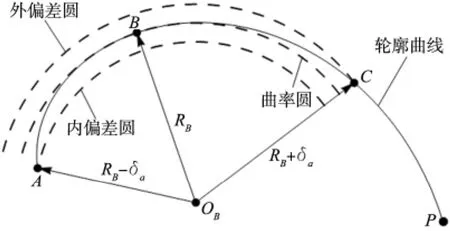
图1 三圆弧插补节点的确定
设点B(xB,yB)为曲线上的一点,记该点的曲率圆圆心为OB,曲率半径为RB,则曲率圆圆心OB(ξB,ηB)及半径RB的计算公式为:
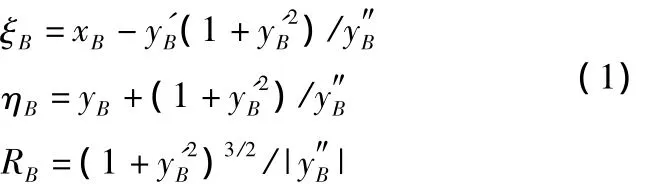
式中,yB=f(xB)为点B的纵坐标,y'B与y″B分别为曲线y=f(x)在点B处的一阶和二阶导数值。
记点A的坐标为(xA,yA),则点B(xB,yB)的坐标可通过求解方程式:

得到。
为求解以上非线性方程式(2),设点D(xD,yD)为曲线上的动点,且其曲率圆圆心为OD,曲率圆半径为RD,同时,构造函数:

则函数z1的零点即为点B的横坐标xB。
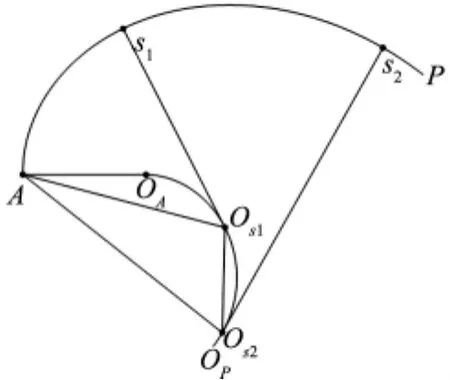
图2 第二个插补节点的确定

式(5)和式(6)表明,当动点D由点A运动到点P的过程中,函数z1单调递增。同时考虑到,当动点D位于点A时,函数z1的值取负值-δa。因此,只要曲线的弧长足够,函数z1的零点存在且唯一,即就是点B存在且唯一。
点B的坐标确定后,由式(1)可求得曲率圆圆心OB(ξB,ηB)以及半径RB。类似地,若构造函数:

且取x∈[xB,xP],则函数z2的零点即为点C的横坐标xC。容易证明,函数z2同样单调递增,且在曲线的弧长足够的情况下,在区间[xB,xP]上存在且仅存在唯一的零点。于是,点C可唯一确定。
1.2 三圆弧的构造方法
当圆弧插补节点A和C确定后,连续相切的三个插补圆弧段分别构造如下:
(1)第一段插补圆弧为过A点且与点A和点B处的曲率圆均相切的圆弧。
(2)第三段插补圆弧为过C点且与点C和点B处的曲率圆均相切的圆弧。
(3)设第一段与第三段插补圆弧与点B处的曲率圆分别相切于点E和点F,则点B处的曲率圆上位于点E和点F之间的圆弧段为第二段插补圆弧。

图3 插补圆弧的构造
如图3所示。若记第一段和第三段插补圆弧(点线)的圆心分别为O1(ξ1,η1)和O3(ξ3,η3),半径分别为R1和R3,且点A和点C处的曲率圆圆心分别为OA(ξA,ηA)和OC(ξC,ηC),半径分别为RA和RC,则应有点A、OA、O1三点共线,点E、O1、OB三点共线,且点C、O3、OC三点共线,点F、OB、O3三点共线,且有:
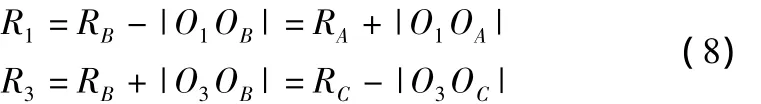
曲率圆圆心OA和OC的坐标以及RA和RC可参照式(1)计算。插补圆弧半径R1和R3通过求解以下两个一元二次方程得到,方程的根仅取R1>RA和R3<RC。

插补圆弧圆心O1和O3的坐标计算公式为:

1.3 三圆弧逼近方法的可行性分析
下面证明点E必位于圆弧段 内。如前所述,轮廓曲线的渐屈线应该是凹向一致且光滑连续的。由渐屈线的性质知:

采用反证法进行证明。假设存在过A点且与点A和点B处的曲率圆均相切的圆弧',它与点B处的曲率圆相切于点E',且点E'位于圆弧段上。记圆弧的圆心为O',且直线OO'与直线OB的A1B交点为点G,见图4。特别地,当点E'与点B重合时,圆心O1'与点G重合。由于圆弧 与点A和点B处的曲率圆分别相切于点A和点B,因此:
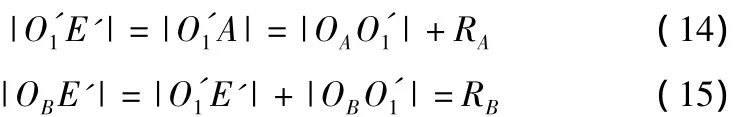
结合式(13)~(15),可得:

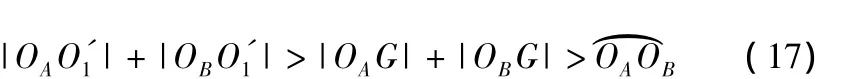
显然,式(16)与式(17)矛盾。
类似地,可以证明点F必位于圆弧段内。因此,所作三圆弧的最大插补误差在容差范围之内,即该三圆弧逼近方法是可行的。
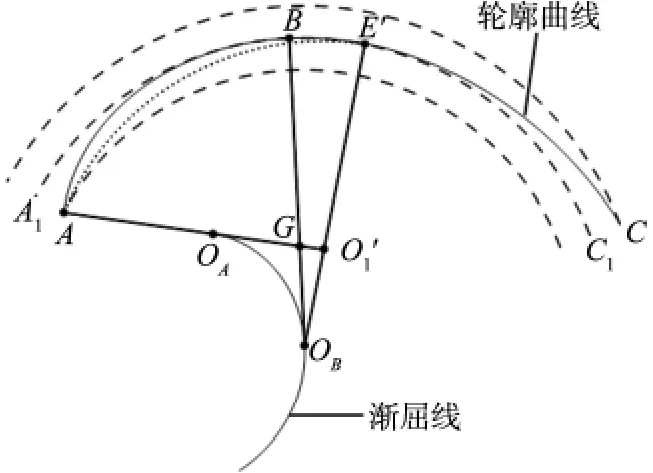
图4 三圆弧相切点的位置
1.4 算法流程
对于任意给定的平面轮廓曲线,三圆弧逼近的总体步骤为:首先在曲线的曲率极值点、拐点以及曲率不连续点处将整个轮廓曲线划分为多段,并通过一定的旋转或镜像变换使每个曲线段都满足曲率连续且单调递减的条件。其次,对每个曲线段分别应用三圆弧逼近方法生成所需的拟合圆弧样条曲线。最后,将所生成的圆弧样条曲线做相应的反变换以连接各部分形成整体轮廓的圆弧样条曲线。
对于每一个经变换后的曲线段(直线段除外),三圆弧逼近的算法流程如下:
(1)记曲线段的起点为A,终点为P,并计算相应的曲率圆圆心OA(ξA,ηA)和OP(ξP,ηP),以及曲率圆半径RA和RP。以k表示当前三圆弧样条曲线段的序号,并令k=1。
(2)分别计算式(3)所定义的函数z1在点A及点P处的函数值,即z1(xA)和z1(xP)。若函数值z1(xA)和z1(xP)异号,则在区间[xA,xP]上求解该非线性函数的零点并计算得到相应的点B;否则,转至第⑤步。
(3)计算点B处的曲率圆圆心OB(ξB,ηB)和半径RB,以及式(7)所定义的函数z2在点B及点P处的函数值,即z2(xB)和z2(xP)。若函数值z2(xB)和z2(xP)异号,则在区间[xB,xP]上求解该非线性函数的零点并计算得到相应的点C;否则,转至第⑥步。
(4)计算点C处的曲率圆圆心OC(ξC,ηC)和半径RC;由式(9)~(12)分别计算当前三圆弧中第一段和第三段插补圆弧的半径R1、R3以及圆心O1和O3的坐标;由OB、O1及点E的位置关系计算点E的坐标,由OB、O3及点F的位置关系计算点F的坐标,并保存R1、RB和R3以及点A、C、O1、OB、O3、E和F的信息后,令k=k+1,并将点C记作点A返回到第②步继续执行。
(5)将点P记作点B并依据式(9)和(11),计算R1和点O1,由OB、O1及点E的位置关系计算点E的坐标,保存R1和RB以及点A、O1、OB、和E的信息后退出。
(6)将点P记作点C并由式(9)~(12)分别计算当前三圆弧中第一段和第三段插补圆弧的半径R1、R3以及圆心O1和O3的坐标;由OB、O1及点E的位置关系计算点E的坐标,由OB、O3及点F的位置关系计算点F的坐标,并保存R1、RB和R3以及点A、C、O1、OB、O3、E和F的信息后退出。
2 数值算例
一椭圆曲线零件,其长半轴为50mm,短半轴为30mm,椭圆方程为:

因椭圆关于X轴和Y轴对称,选第二象限进行圆弧插补,则所选曲线段的曲率连续且单调递增,无需进行图形的旋转或镜像变换。
设插补容差为δa=0.01mm,采用文中所提的三圆弧逼近方法,得到的三圆弧7组共20段圆弧,圆心坐标及半径如表1所示。

表1 各圆弧段的中心及半径 (单位:mm)
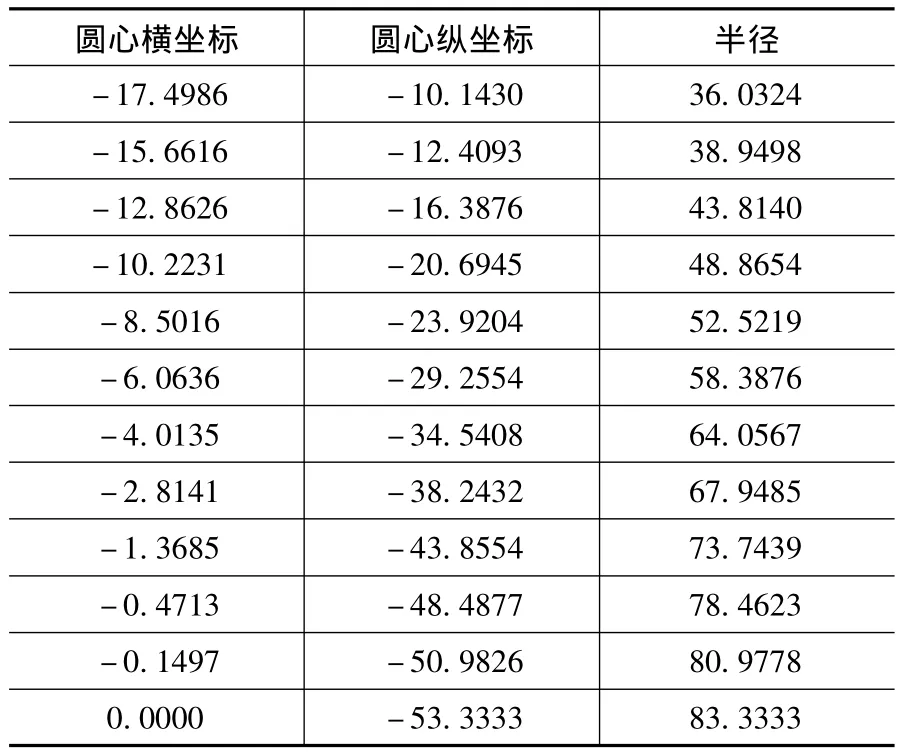
(续表)
3 结论
(1)论文提出了一种三圆弧逼近非圆曲线的方法,并证明了该方法的可行性。
(2)论文所提方法采用曲率圆以及相应的偏差圆来确定插补节点并构造连续相切的圆弧,计算简单,误差控制直接,便于工程应用。
[1]徐建明,刘飞,何援军,等.离散点列的局部双圆弧逼近[J].东华大学学报(自然科学版),2005,31(4):62 -65.
[2]乐英,韩庆瑶,王璋奇.数控加工中非圆曲线的最小二乘圆弧逼近[J].华北电力大学学报,2006,33(6):102 -104.
[3]虞铭财,杨勋年,汪国昭.整体最优双圆弧拟合[J].高校应用数学学报A辑,2004,19(2):225-232.
[4]蔡慧林,戴建强.基于遗传算法的相切圆弧逼近非圆曲线算法[J].兰州交通大学学报(自然科学版),2007,26(6):5-9.
[5]岳秋琴,蒋幸幸.数控编程中圆弧逼近非圆曲线的数据处理[J].机械研究与应用,2003,16(3):56-60.
[6]张洪江,侯书林.数控机床与编程[M].北京:北京大学出版社,2009.
[7]陈明君,赵清亮,董申,等.基于双圆弧步长伸缩数控插补非圆曲线算法的研究[J].机械工程学报,2003(39):111-116.
[8]张莉彦,邱辉,陈虎,等.平面曲线的双圆弧最佳逼近[J].组合机床与自动化加工技术,2002(12):34-36.
[9]关耀奇.双圆弧逼近在椭圆零件加工中节点值的求解[J].组合机床与自动化加工技术,2003(1):59-60.
