基于多色集合理论的机械零件加工路线方法研究*
2013-09-12祝天荣徐新胜陶西柱
祝天荣,徐新胜,陶西柱
(中国计量学院质量与安全工程学院,杭州 310018)
0 引言
随着科技的进步,人们对所需产品的要求也越来越高。对于机械产品,伴随着计算机技术的发展,生产商则面临着结构复杂、小批量、多品种、生产周期短以及低成本和高质量的生产要求。促使生产制造商采用先进的制造技术和生产模式。俗话说“机械制造,工艺为本”,任何先进的产品设计,都要在工艺保证的前提下进行。工艺水平直接影响产品质量,因此一个产品的工艺设计过程中,工艺加工路线的选择和确定是至关重要的环节。加工路线是指将零件上所有加工对象的加工方法按照一定的方法、规则组成的相关排列顺序。由于加工方法以及加工对象的多样化,加工要求的个性化以及决策过程的经验性,使得加工工艺的决策尤为困难。针对工艺决策,人们常用的方法有传统决策方法决策表和决策树、采用专家系统、基于遗产算法数学建模等方法,每种方法各有不同的特点。应用传统决策方法,决策知识和算法并不能独立;采用专家系统,可以解决传统决策方法的不足;基于遗传算法的数学建模,虽然解决了加工工艺路线问题,但是所得到的最优路线,只是一定范围内的最优解,带有一定的局限性。本文则是采用一种新的系统分析工具——多色集合理论,进行机械零件加工路线的确定。并且以箱体类零件为例验证该理论的可行性。
1 箱体类零件加工路线分析
箱体类零件是机器或部件的基础零件,它主要包括一些轴、套、齿轮等相关零件。所以加工一个箱体类零件时,面临的加工对象有平面、槽、凹坑、光孔、锥孔和螺纹孔等。针对不同的加工对象,所采用的加工方法和加工工具各有不同。对于平面加工一般方法是铣削、刨削和磨削,而箱体零件上对孔、孔距以及相互位置的精度要求都比较高,常用的孔的加工方法是钻、扩、镗和铰。
箱体零件的加工过程一般可以分为粗加工、半精加工、精加工和光整加工等四个阶段。在实际的生产加工过程中,选择加工工艺路线时,不仅要遵循先面后孔,粗精分开、先粗后精,先基准再其它以及工序集中、先主后次的基本原则,并且要考虑到产品成本及经济效益问题。所以,如何快速准确的得到产品加工工艺路线和选择出最佳路线是我们急需解决的问题。
2 多色集合理论
2.1 多色集合理论基本思路
传统的集合是指所有元素的全体,在该集合中元素仅仅是名字的不同,它并不能描绘集合本身以及组成元素的其他相关性质。基于如何扩大普通集合论仿真可能性的思想,俄罗斯Pavlov V V教授(国际信息学院院士,CAD CAM CAE委员会副主席)提出了一种新的系统理论工具——多色集合理论,在整个研究过程中,于1988年产生了多色图的概论,1995年产生了多色集合的概念,2000年提出了多色集合的体系结构。
多色集合理论的核心思想是使用标准的数学模型来仿真不同的对象(产品、设计过程、工艺过程、生产系统)。在多色集合中,集合本身和集合中所有的元素都将会被涂上不同的颜色来表示其全部不同的性质,这是传统集合所不能满足的特征之一。
2.2 多色集合理论基本概念
对于多色集合A=(a1,…,ai,…,an),元素ai的个人颜色集合为F(ai)=(f1,…,fi,…,fk),其中ai∈A。F(a)是所有元素个人颜色的集合。集合A的统一颜色为F(A)=(F1,…,Fj,…,Fm),其中Fj对应着集合A的第j个性质。一般情况下F(A)≠F(a),也就是说,多色集合的性质一般并不是其所有组成元素性质的简单叠加。
多色集合所有元素的个人颜色可以用布尔矩阵表示为:
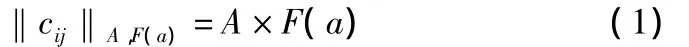
如果Fj∈F(ai),则cij=1,否则cij=0。
元素的个人颜色和多色集合统一颜色之间的相关关系可以用布尔矩阵表示为:

如果个人颜色fi影响到统一颜色Fj的存在,那么cij=1,否则cij=0。
多色集合统一颜色和其组成元素之间的相关关系可以用布尔矩阵表示为:
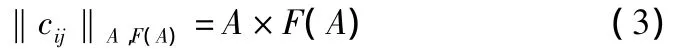
如果元素ai影响到统一颜色的存在,那么cij=1,否则cij=0。
多色集合元素的组成是颜色Fj(A)的体Ak(Fj),统一颜色的体用布尔矩阵可表示为:
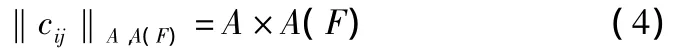
其中A(F)是统一颜色所有体的集合。
综上所述,多色集合是由6个成分确定的,其具体的表示为:

3 多色集合理论的加工路线建模
现实生产系统中普遍存在着层次结构,为了得到我们所要加工工件的加工路线,需要对工件加工系统逐层分解,分成若干层,每层包括目标、方法,因此我们可以应用多色集合的层次递阶结构对加工过程进行建模。
针对层次递接结构我们进行多色集合定义,我们把每个过程方法定义为元素ai,元素具有统一颜色F(A)和个人颜色F(ai)。统一颜色指该方法所要实现的目标。个人颜色就是对该方法的具体描述,其分为两种情况:如果该方法不是最底层的操作,那么可以将该方法看成是下一层的目标,也即上层的个人颜色是下一层的统一颜色;若该方法不能再分解,那么个人颜色就是该方法的描述。在每层中,从目标到方法的推理矩阵,在多色集合中我们用个人颜色与统一颜色的关系矩阵来表示,有的时候也附带推理矩阵的约束条件,这个是推理过程的核心内容。
应用多色集合建模及应用步骤如下所示:
步骤1:根据给出的机械零件图,找出所要加工的具体对象目标,建立递接层次结构图,得到,…,的值,并将这些值用布尔向量表示,满足目标要求为1,否则为0。
步骤2:由个人颜色与统一颜色的关系矩阵、元素与个人颜色之间的关系矩阵及其对应的约束条件,找出相应可行的方案。
步骤3:根据生产的经济性和实际性选出最佳方案路线。
4 实例分析
某箱体零件的零件简图如图1所示。
根据零件简图以及加工工艺的相关规则,应用多色集合进行递阶结构的建模。如图2所示,对递阶结构图进行多色集合描述,其中:
方法层(加工工序):a1为粗铣;a2为半精铣;a3为精铣;a4为粗刨;a5为半精刨;a6为精刨;a7为粗镗;a8为半精镗;a9为精镗;a10为钻孔;a11为粗铰;a12为精铰;a13为攻丝。
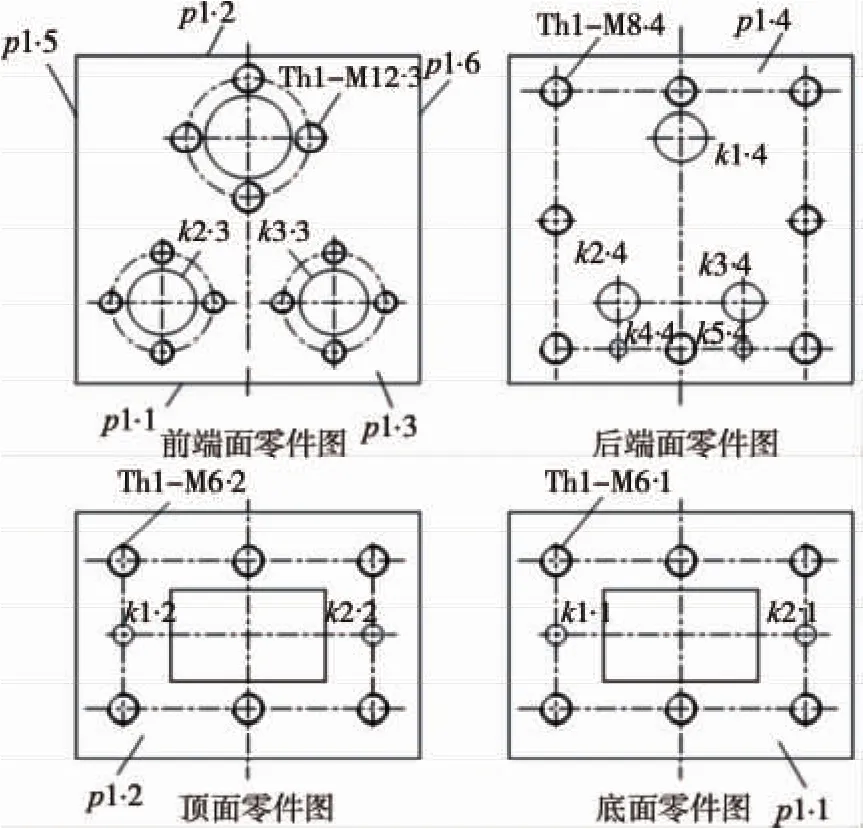
图1 箱体零件的结构简图

图2 箱体零件递阶结构图

图3 个人颜色与统一颜色以及元素与个人颜色之间的布尔矩阵图
根据上面的分析,我们可以在遵循加工工艺规则以及确定基准的情况下,对所得到的加工工序进行合理的编排,进而得到零件的加工路线,具体方法在此不一一说明。最后我们可以得到该零件的加工工艺路线为:①粗刨(粗铣)p1.1~p1.6;②半精刨(半精铣)p1.1~p1.6;③精刨(精铣)p1.1~p1.4;④粗镗k1-3.3,k1-3.4;⑤钻Th1-M6.1,k1-2.2,Th1-6.2,Th1 -M12.3,k4 -5.4,Th1 -M8.4;⑥半精镗k1-3.3,k1-3.4;⑦粗铰k1-2.2,k4-5.4;⑧攻丝Th1-M6.1,Th1-M6.2,Th1-M12.3,Th1-M8.4;⑨精镗k1-3.3,k1-3.4;⑩精铰k1-2.2,k4-5.4。
由上述理论得到的工艺路线可知,基本上是符合典型加工路线的。由此可见,应用多色集合理论进行加工路线的选取是可行的。
5 结论
通过本例的验证,说明在零件加工工艺中,应用多色集合理论建模,能够快速的选择满足生产要求的工序,并根据相关准则,编制零件加工工艺路线。由此说明了多色集合的灵活性和实用性,目前国内对多色集合理论及其应用的研究还很少,有待我们进一步深入研究。
[1]陈红霞.机械制造工艺学[M].北京:北京大学出版社,2010.
[2]于俊一.典型零件制造工艺[M].北京:机械工业出版社,1989.
[3]朱景,李宗斌,高新勤,等.基于多色集合的工作流建模及路径求取算法[J].西安交通大学学报,2006,40(3):348-352.
[4]张博,张洪涛,赵珊珊,等.基于多色集合理论的产品装配规划建模与算法研究[J].西安交通大学学报,2005,39(11):1254-1258.
[5]袁林忠,伍宪彬.遗传算法在机械零件加工工艺决策中的应用和实现[J].机械设计与制造,2005(1):73-75.
[6]Pavlov V V.M a them a tics simulation of discrete production system[J].Information Technology,1995(0):15 -19.
[7]唐永刚,李宗斌,李善仓.基于多色集合理论的概念设计形式化解决方法[J].西安交通大学学报,2004,38(1):68-72.
[8]Pavlov V V.Polychromatic sets and graphs for CALS in machine building[M].Moscow:Stankin Press,2002:20 -35.
[9]Li Z B,Xu L D.Polychromatic sets and its application in simulating complex objects and systems[J].Computers&Operations Research,2003,30(6):851 -860.
