应用含参量定积分证明Wallis公式*

何郁波，王 亚，罗思雯，彭 丽

(1.怀化学院数学系，湖南怀化 418008;2.湖南省岳阳县杨林中学，湖南岳阳 414115)

应用含参量定积分证明Wallis公式*

何郁波1，王 亚1，罗思雯1，彭 丽2

(1.怀化学院数学系，湖南怀化 418008;2.湖南省岳阳县杨林中学，湖南岳阳 414115)

利用一个含参量的定积分，给出了Wallis公式的一个新的证明方法.

Wallis公式;含参量定积分;迫敛性

Wallis公式为

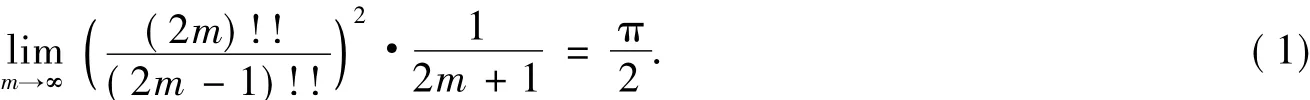
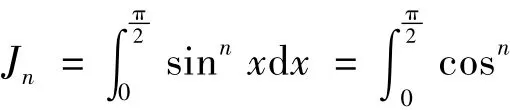
引理1设J(m，n)

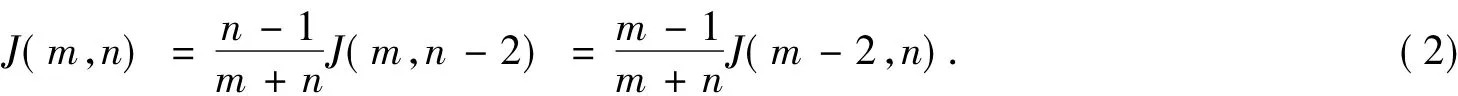
证明因为

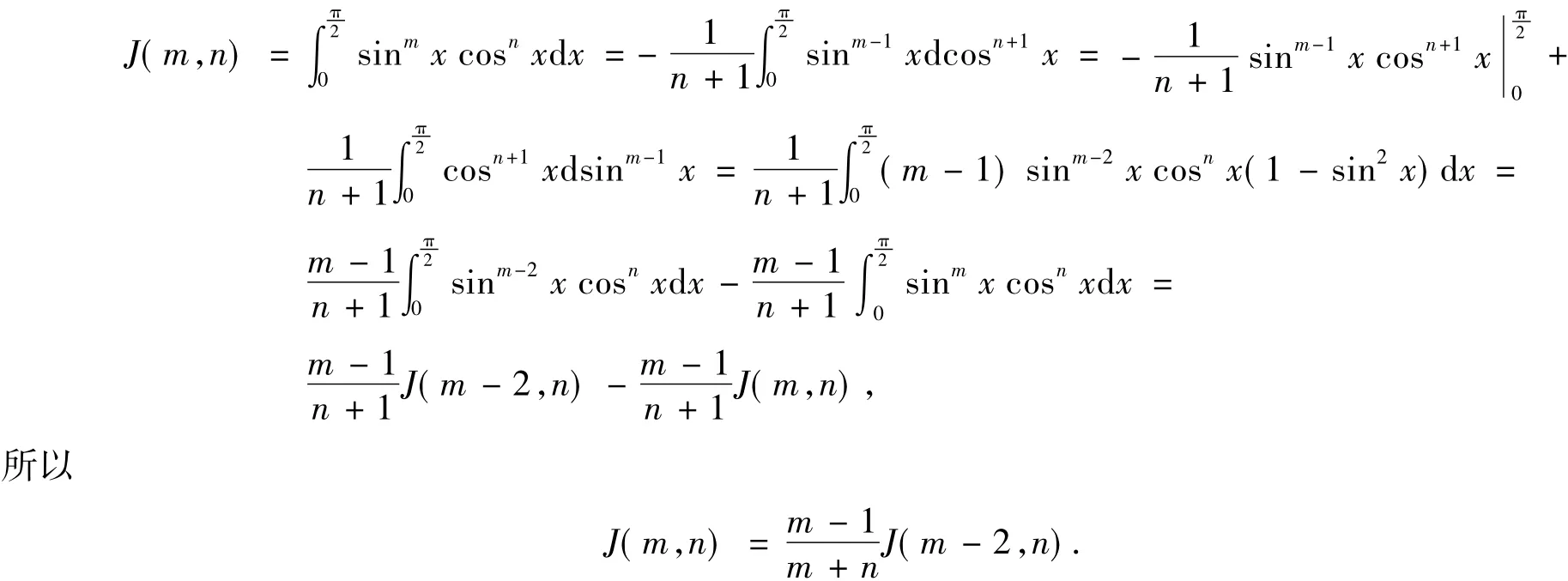
类似可证得

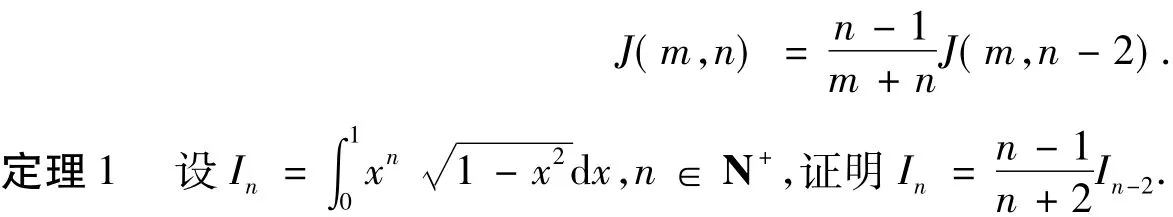
证明令x=sint，由引理1有

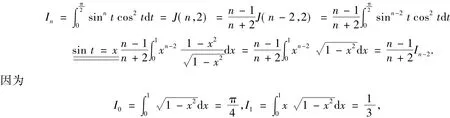
所以由定理1可知，当n=2m(m=1，2，…)时，有

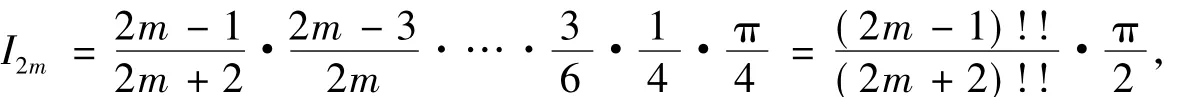
当n=2m+1(m=0，1，2，…)时，有

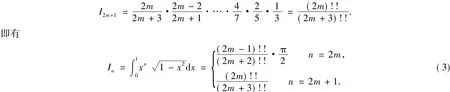
另一方面，根据定积分的保不等式性质知，当x∈(0，1)时，有

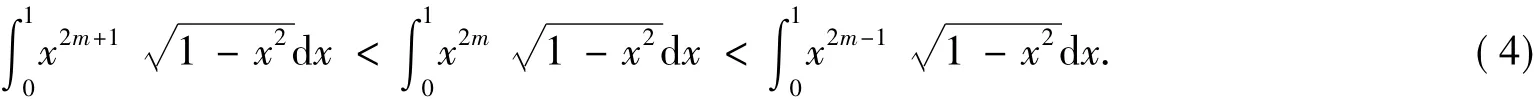
由(3)，(4)式即得

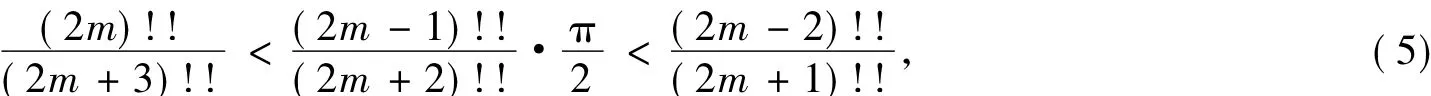
从而由(5)式可得

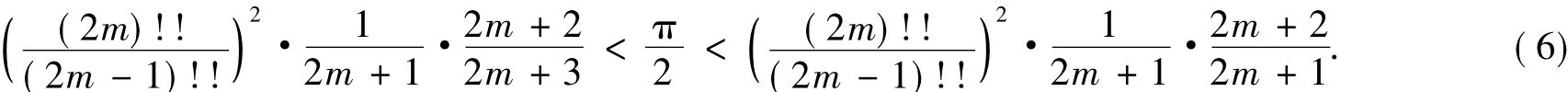
此即Wallis公式.

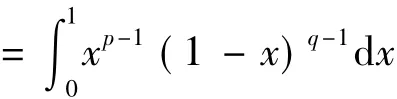
此定理1的证明也可以采用如下证明方法:

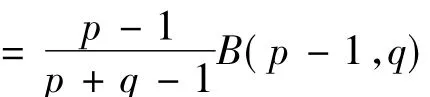
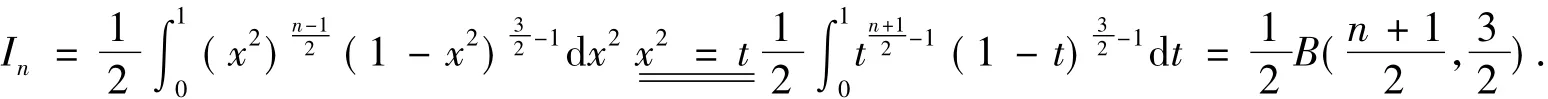
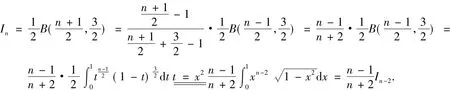
［1］ 华东师范大学数学系.数学分析(上册)［M］.北京:高等教育出版社，2001.

［2］ 刘玉琏，傅沛仁.数学分析讲义(上册)［M］.北京:高等教育出版社，2008.

［3］ 刘 证.Wallis公式的一个新证明［J］.高等数学研究，2005，8(1):14-17.

(责任编辑 向阳洁)

Applying Definited Integral with a Parameter to Prove the Wallis Formula

HE Yu-bo1，WANG Ya1，LUO Si-wen1，PENG Li2
(1.Department of Mathematics，Huaihua Uvinersity，Huaihua 418008，Hunan China; 2.Yanglin Middle School of Yueyang County，Yueyang 414115，Hunan China)

A definite integral with a parameter is applied to design a new way to prove Wallis Formula.

Wallis formula;definite integral with a parameter;squeeze theorem

O178

A

10.3969/j.issn.1007-2985.2013.02.004

1007-2985(2013)02-0019-03

2012-10-23

怀化学院教改项目(201031)

何郁波(1979-)，男，湖南岳阳人，怀化学院数学系讲师，硕士，主要从事非线性互补问题与微分方程数值解研究.