一类广义格路的计数*

唐保祥，任 韩

(1.天水师范学院数学与统计学院，甘肃天水 741001;2.华东师范大学数学系，上海 200062)

一类广义格路的计数*

唐保祥1，任 韩2

(1.天水师范学院数学与统计学院，甘肃天水 741001;2.华东师范大学数学系，上海 200062)

连结m×n的棋盘上一对对角顶点的路称为广义格路.利用限位排列计数方法，得到m×n的棋盘上长为m+ n+2的广义格路的计数公式.

棋盘;广义格路;字符序列;双射

1 基本概念

通常2维平面上的格路是平面棋盘上沿着方格的边向右、向上行进的一条路.格路计数的方法和已有结果，在组合计数和组合恒等式的证明中有一定应用［1-9］.文中所指的广义格路，是平面棋盘上沿着方格的边向左、向右、向上和向下4个方向都可以行进且不相交的格路.

为了研究问题不产生歧义，给出下面精确定义.

定义1将宽和长分别为m和n个单位的矩形的长和宽分别m和n等分，再依次分别连结对边上的等分点，所得图形称为一个m×n的棋盘，记作Qm×n.

定义2设A和B是m×n的棋盘Qm×n上最大矩形的一对对角顶点，棋盘Qm×n上一条沿着小方格的边向左、向右、向上和向下4个方向都可以行进且不相交的由A到B的路，称为Qm×n上A到B的一条广义格路.

对任意正整数m和n，棋盘Qm×n上A到B的所有广义格路有多少条，至今未见到相关结果的文献.笔者用限位排列计数方法，得到了m×n的棋盘Qm×n上一对对角顶点间长为m+n+2的广义格路的显式计数公式.

设S1是由字符x，y和y-1形成的满足下列3个条件的字符序列的集合:

定理1设有i个字母a，j个字母b，k个字母c，1≤i＜j.将这些字母排成字符串，要求若i＞1，每2个相距最近的a之间至少有1个b，且最左边的字母a的左边和最右边的字母a的右边至少各有1个b.设f(i，j，k)表示满足上述要求的所有字符串的个数，则

在如今电动网联化的大趋势下，轻量化显得尤其的重要。减轻汽车车身的质量能在一定程度上增加电动车的里程，降低能耗。由于在汽车零部件的结构件中，常用的材料是玻纤增强型的复合材料，将振动力场引入复合材料注塑的全过程，能够增强和优化玻纤的取向，降低剪切力场对玻纤的破坏，从而达到提高制品力学性能的目的，给结构设计师提供了对制品进行优化的空间，实现制品的轻量化。

证明显然集合S1和S2都是有限集合，且只有m=n=1时，S1=S2=Ø，结论成立.下面假设m= n≥2.做集合S1到S2的对应法则f如下:∀l1∈S1，将序列l1中的每个x换成y，每个y换成x，将y-1换成x-1，将上述变换所得的新字符序列记为l2，即f(l1)=l2，则l2∈S2.易知f是集合S1到S2的双射，所以

(2)字符串xy-1x在S1的每个字符序列中都以整体形式恰出现1次(在S1的字符序列中算3个字符);

对于中国农民而言，“纠纷宝塔理论”所刻画的由下至上的纠纷解决层级结构并非是一个需要“攀爬”的实体[14]，而是一个可以灵活选择而跳跃达至的扁平结构。乡土正义系统是纠纷解决过程中以农民的法律资源选择为主的法律秩序公共品集合体。就本文的分析所及，乡土正义供给系统看似具有层级性，但在农民进行法律资源选择的过程中，正义系统中的部件结构却是扁平化的，农民既可以找村干部调解纠纷，也可以向派出所寻求帮助，也可以综合利用乡镇政府的熟人关系网络来促成纠纷的解决。

(1)S1的每个字符序列的长度均为m+n+2，其中恰有1个y-1，m+1个y，n个x;

(3)S1的每个字符序列中，xy-1x作为一个整体，在其之前和之后至少各出现1个字符y.

其二，英国国内以牛津为中心，掀起了轰轰烈烈的天主教复兴运动，力图洗涤生活在工业文明尘埃下的国人日益模糊的信仰，唤醒他们心中的纯洁本质。此项运动为拉斐尔前派的诞生做好了精神铺垫。

(3)S2的每个字符序列中，yx-1y作为一个整体，在其之前和之后至少各出现1个字符x.

(2)字符串yx-1y在S2的每个字符序列中都以整体形式恰出现1次(在S2的字符序列中算3个字符);

(1)S2的每个字符序列的长度均为m+n+2，其中恰有1个x-1，n+1个x，m个y;

2 主要结果及其证明

废了抛光技术我还混个逑？除了抛光，我啥也不会。我在大发厂打了六年工，天天戴口罩，戴手套，和抛光机打交道。多复杂的异型产品，再多的瑕疵，到了我手里，往抛光机上一抛，麻子也能放光彩。林老板是赏识我的，有意栽培我，去年刚提我当了抛光课长。谁知才一年，我就提出辞工了。其实我也没料到，要不是阿花三番五次地催我，我不会考虑辞工。

RC4目前应用范围十分的广泛，它被应用在SSL/TLS(安全套接字协议/传输层安全协议)标准中，以及作为无线局域网标准的一部分，还被应用在无线系统以保证无线链路的安全。从各种各样的应用，我们可以看出来RC4算法是目前网络通信的重要组成部分，这个算法非常的重要。

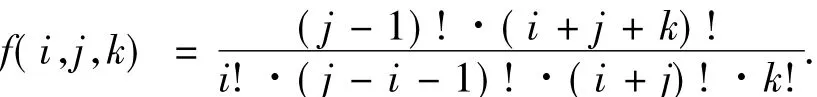
设S2是由字符x，y和x-1形成的满足下列3个条件的字符序列的集合:

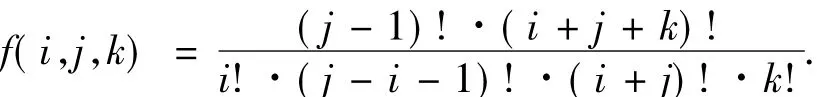
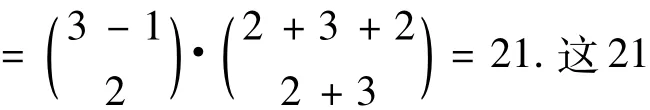
定理2对上述字符集合S1和S2，若m=n，则有

科技查新事实型数据应用的重点是：基于数据库围绕查新人员或机构、研究领域以及创新主题，开展数据的挖掘和信息统计分析服务，为政府决策提供参考，为科研人员的课题选择提供信息服务。研究的侧重点在于将科技查新数据应用到企业技术创新研究中，从科技查新事实型数据库来推演分析企业的技术创新活动，尤其是基于湖北省科技查新数据库，从企业的产品创新出发，识别出全省的新兴产业、前沿产业和重点产业，并通过关联分析，找出技术创新、企业发展和产业升级的痛点，精准推演政策需求，并通过实证研究，为科技企业培育工程的精准施策提供更有价值的参考。

定理3设A和B是m×n的棋盘Qm×n上最大矩形的一对角顶点，P是棋盘Qm×n上由A到B长为m +n+2的广义格路的集合，对上述字符序列集合S1和S2，令S=S1∪S2，

证明显然S1∩S2由A到B的一条广义格路，若在整个路途中共向右走了n步，向上走了m+1步，向下走了1步，称之为p1类广义格路;若在整个路途中共向右走了n+1步，向上走了m，向左走了1步，称之为p2类广义格路.对由A到B的一条广义格路，每向右走1步，顺次记1个字符x;向上走1步，顺次记1个字符y;向左走1步，顺次记1个字符x-1;向下走1步，顺次记1个字符y-1.那么对∀pi∈P，若i =1，就唯一得到S1的字符序列l1;若i=2，就唯一得到S2中的字符序列l2.反之，对∀l1∈S1，则唯一对应于P中一条p1类广义格路;∀l2∈S2，则唯一对应于P中一条p2类广义格路.所以集合P和S间存在一个双射，从

定理4设A和B是m×n的棋盘Qm×n上最大矩形的一对角顶点，P是棋盘Qm×n上由A到B长为m +n+2的广义格路的集合，令f(m，n)

消费的转型升级无形中提升了生活质量，因此人们对高品质生活的追求促进了新电商的发展，大数据时代下能清晰了解消费群体的喜好，因此商户能够相对科学判断消费者的需求，从而为特定人群匹配相应产品，从而降低成本同时还提高了服务质量。

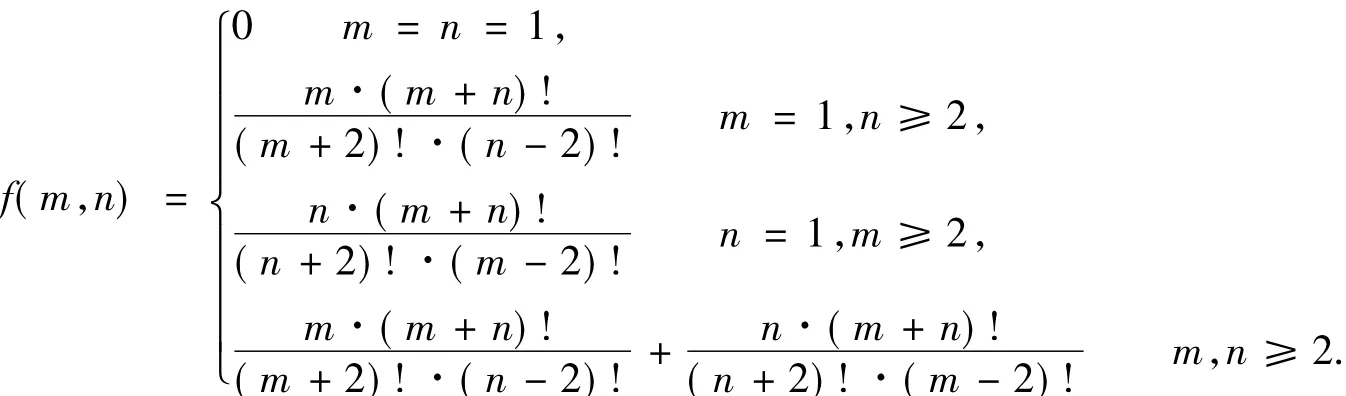
证明由定理3知，对给定的m，n，需要求

情形1m，n≥2.

对于S1的字符序列，将xy-1x作为一个整体看成字母a，将y看成字母b，将x看成字母c，由S1的定义知，S1中的每个字符序列唯一对应着一个满足定理1条件的有1个a，m+1个b，n-2个c的字符串;对于S2的字符序列，将yx-1y作为一个整体看成字母a，将x看成字母b，将y看成字母c，由S2的定义知，S2中的每个字符序列唯一对应着一个满足定理1条件的有1个a，n+1个b，m-2个c的字符串.因此由定理1知，

例22×3的棋盘一对对角顶点间共有f(2，3)=13条长度为7的广义格路，这13条广义格路以及对应的字符序列如图1所示.

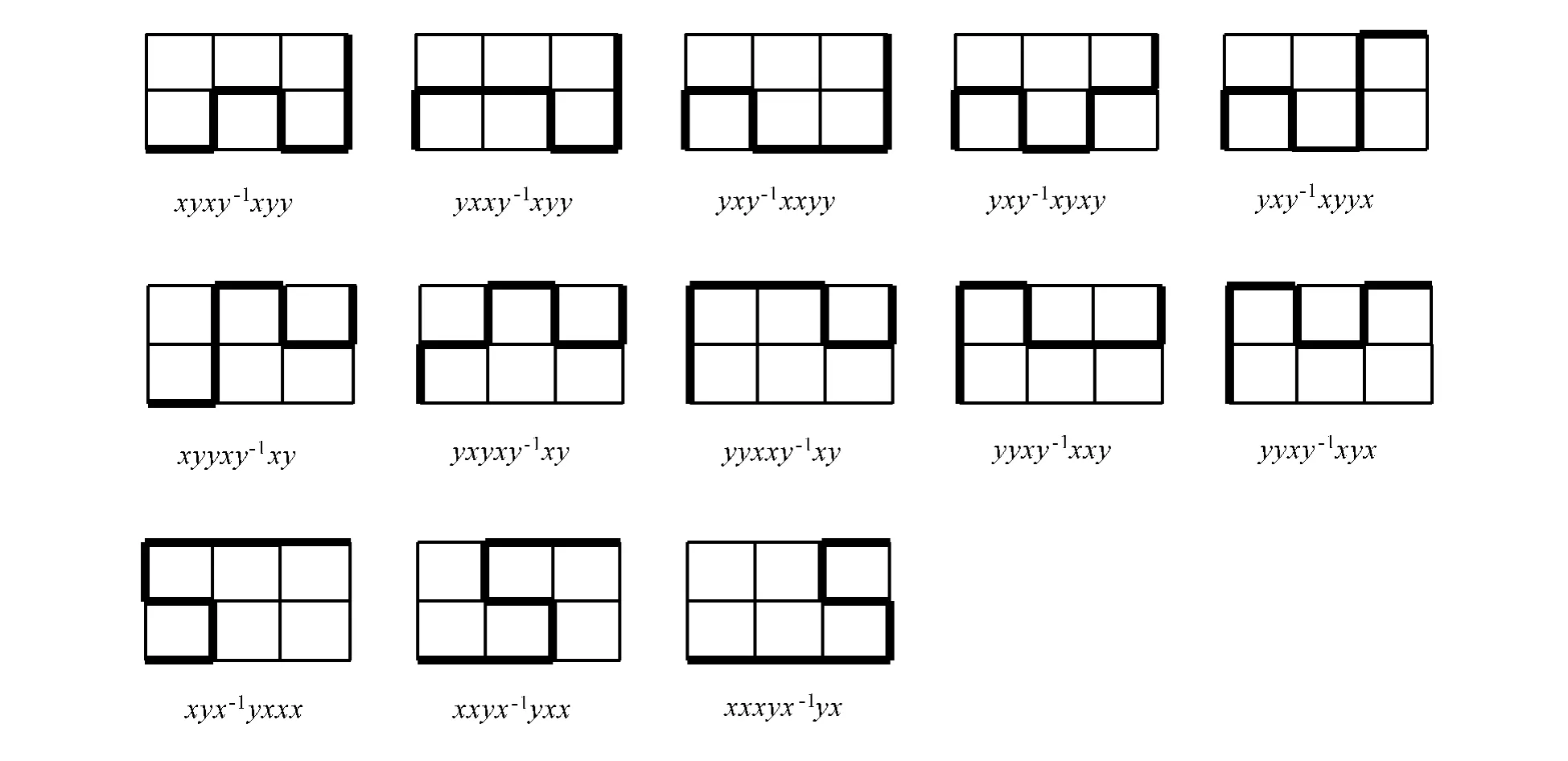
图1 2×3棋盘一对对角顶点间的13条广义格路

［1］ MOSER L，ZAYACHKOWSKY W.Lattice Paths With Diagonal Steps［J］.Scripta Math.，1963，26:223-229.

［2］ CHU Wen-chang.On the Lattice Path Methods in Convolution-Type Combinatorial Identities［J］.Chinese Quarterly Jounal of Mathematics，1988，3(4):1-5.

［3］ KAPARTHI S，RAO H R.Higher Dimensional Restricted Lattice Paths with Diagonal Steps［J］.Discrete Appl.Math.，1991，31:279-289.

［4］ 初文昌.格路计数与经典分拆恒等式［J］.系统科学与数学，1992，12(1):52-57.

［5］ 王天明，马欣荣.格路与组合恒等式［J］.大连理工大学学报，1994，34(6):628-632.

［6］ 王天明，马欣荣.格路与Vandermonde卷积恒等式［J］.大连理工大学学报，1996，36(6):639-644.

［7］ LU Qing-lin.A Note on Lattice Paths with Diagonal Steps in Three-Dimensional Space［J］.Journal of Mathematical Research and Exposition，2005，25(3):447-450.

［8］ 王恒亮，陈晶晶，王 燕.几个格路计数问题的推广［J］.天津城市建设学院学报，2006，12(3):234-236.

［9］ 常海廷，卢青林，陈美娟.基于格路模型的组合恒等式及其证明［J］.徐州工程学院学报:自然科学版，2009，24(2):7 -9.

(责任编辑 向阳洁)

Counting of One Kind of Generalized Lattice Path

TANG Bao-xiang1，REN Han2
(1.School of Mathematics and Statistics，Tianshui Normal University，Tianshui 741001，Gansu China; 2.Department of Mathematics，East China Normal University，Shanghai 200062，China)

The generalized lattice path is made by joining path which is on a pair of diagonal vertices on the chessboard ofm×n.The counting formula of the generalized lattice path whose length ism+n+2 on chessboard ofm×nhas been obtained by using the counting method of the spacing permutations.

chessboard;generalized lattice path;character sequence;bijection

O157

A

10.3969/j.issn.1007-2985.2013.02.001

1007-2985(2013)02-0001-04

2012-12-02

国家自然科学基金资助项目(11171114)

唐保祥(1961-)，男，甘肃天水人，天水师范学院数学与统计学院副教授，主要从事图论和组合数学研究.