AHP问题的研究及应用*

徐永琳

(西北民族大学数学与计算机科学学院，甘肃兰州 730030)

AHP问题的研究及应用*

徐永琳

(西北民族大学数学与计算机科学学院，甘肃兰州 730030)

层次分析法(AHP)是经典的多属性决策方法，在很多领域得到了应用.研究AHP的基本理论，给出了确定权重的AHP方法，描述了采用AHP解决多目标决策问题的方法和步骤，通过具体消费者购房的实例，为消费者的实际消费决策提供科学合理的方法.

AHP;判断矩阵;标度;多目标决策;权重

层次分析法(Analytic Hierarchy Process，简称AHP)是由美国运筹学家，匹兹堡大学T.L.Saaty教授于20世纪70年代初期提出的，它通过构造层次结构和比率分析可以将各属性上决策者定性的判断与定量的方向结合起来，将各种因素层次化，并逐层比较多种关联因素，为分析和预测事物的发展提供可定量依据，提供了人类决策思维活动的有效性和机动性.AHP的原理基于矩阵论和实验心理学研究，结构明确、简单易懂，能被各个领域的人快速掌握，使用AHP的关键点是使决策者形象化地使用属性层次结构来构造复杂的多属性决策问题成为可能，对于复杂和较大的递阶层次结构问题，使用AHP更具有鲁棒性［1］.

1 基本概念

定义1(有序集)若集合E中所有的元素都满足自反性、对称性和传递性，则称E为有序集;若还满足完备性，则称为整体有序集，否则称为局部有序集.

定义2E为有序集，∀x，y∈E，记

定义3设H是带有惟一最高元素c的有限的局部有序集，若它满足如下条件，则称H为一个递阶层次:

(1)存在H的一个划分{Lk}(k=1，2，…，m)，其中L1={c}，每个划分Lk称为一个层次;

(2)对于每个x∈Lk(1≤k≤m-1)，X-非空且X-⊆Lk+1;

(3)对于x∈Lk(2≤k≤m)，X+非空，且X+⊆Lk-1.

定义4以每2个方案(或子目标)的相对重要性为元素的矩阵称为判断矩阵.判断矩阵是层次分析法的核心.判断矩阵的元素aij具有3条性质:(1)aii=1;(2)aij=1/aji;(3)aij=aik·akj.判断矩阵的元素aij可以利用决策者的知识和经验估计出来.

定义6［2］对于正互反矩阵A=(aij)n×n，若满足aij×ajk=aik，则称A为一致性矩阵.它满足:

(1)若A一致，则AT也一致;

(2)A的每一行均为任意指定的另一行的正数倍，从而r(A)=1;

(3)A的最大特征根λmax=n，其余特征根皆为0;

(5)当A为正互反判断矩阵时，它的归一化的右主特征向量w=(w1，w2，…，wn)T就是其排序权向量.

AHP的基本思想:将复杂问题分解为若干层次，在最低层次通过两两对比得出各因素的权重，经过由低到高的层层分析计算，最后计算出各方案对总目标的权数，权数最大的方案即为最优方案.

2 AHP的基本步骤

2.1 分析系统中各因素间的关系，建立系统的递阶层次结构模型

首先将决策系统中各因素之间的关系条理化、层次化，在深入分析的基础上按目标层、准则层、方案层划分出各层次，建立一个有效合理的递阶层次结构模型，对于成功解决问题具有决定性意义.

2.2 构造正互反矩阵

构造正互反矩阵是将每一层元素针对上一层因素所涉及的相互之间的重要性做出比较，将比较的数值直接用矩阵形式表示出来.正互反矩阵可以清楚地表示上一层因素支配的下层有关因素之间的相对重要性.构造两两比较的判断矩阵.选定上一层次中某个确定的准则，对本层次的各个元素关于这个准则的相对重要性进行两两比较，选用合适的标度对这些重要性程度进行合理的赋值，从而构造出一个阶数与被比较元素数目相同的判断矩阵;在进行两两比较时，假设专家组能够比较在递阶结构同一层次的任意2个元素Bi和Bj，并提供它们重要性比率的数值bij(这一层有n个元素).若元素Bi优于Bj则bij＞1;相应地，反过来的性质也成立.根据判断矩阵的互反性，对于一个由n个元素构成的判断矩阵只需给出其上(或下)三角的n(n-1)/2个判断即可.判断矩阵中的每个元素可通过表1给出的绝对数标度产生［3］，从而计算出元素重要性的比率.表1中量化等级时所用1～9标度的描述性解释表示等级的级差是等间隔的，选择1～9之间的整数及其倒数作为量化标度的主要原因是它符合人们进行判断时的心理习惯.许多实验心理学研究亦表明，普通人在对一组事物的某种属性同时作比较，并使判断保持满意的一致性时，所能正确辨别属性的等级或事物的个数一般在5～9个之间［4］.

Saaty等取1～9且级差为1的离散数作为定性等级的量化值，并基本获得社会认同，得到广泛应用.

表1 绝对数标度的基础

2.3 计算元素相对权重并做一致性检验

根据所得到的正互反矩阵，计算对于上一层因素而言的本层次各因素间的相对权重，通常采用和法、特征值法、方根法等求解相对权重.

(1)和法.对于一个一致的正互反矩阵A，它的每一列归一化后就是相应的权重向量.当A不一致时每一列归一化后近似于权重向量，和法就是采用这n个列向量的算术平均作为权重向量.

(2)几何平均法.将A的每个列向量采用几何平均，然后归一化，得到的列向量就是权重向量.其公式是

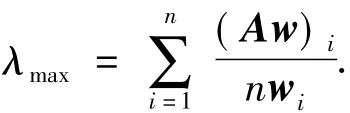
(3)特征根法.它是用来求解A的特征根，Aw=λmaxw(λmax是A的最大特征根，w是相应的特征向量)，得到的w经归一化后就可作为权重向量.

具体步骤:

成立时，则w=wq+1为所求A矩阵最大特征根λmax对应的权重特征向量w，且

这几种权重计算方法各有特点且可以相互转化，最简单易用的方法是矩阵行和归一化方法，从拟合角度出发得到的最小二乘法、对数最小二乘法等也各具优点，对数最小二乘法计算简便，在模糊决策、群组判断和残缺判断等问题中得到了应用.在精确程度不高的情况下，和法、几何平均法均可用来近似计算w和λmax［5］.由于相互比较矩阵可能具有不一致性，特征根法产生的结果考虑了这种因素，它较早被提出并得到广泛应用，Saaty建议使用特征根法［5-6］，它对AHP的发展有重要作用，对于具有模糊性的定性指标的准确量化和指标权重的准确赋值至今仍有较大的难度［7］.除此之外，其他权重计算方法还有最小偏差法(LDM)、梯度特征向量法(GEM)、非线性特征根法等.

2.4 一致性检验

在构造正互反判断矩阵时，由于客观事物的复杂性，主体认识的局限性和多样性，判断经常伴随有误差判断矩阵一般不可能具有完全一致性，因此AHP方法要求对n阶判断矩阵作n(n-1)/2次两两比较，最终导出一个比较合理的反映决策者判断的排序.Saaty等［5］总结出下述一致性检验的方法步骤.

(ⅰ)计算一致性指标CI(consistency index).

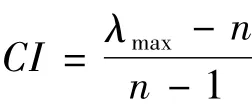
(ⅱ)查找相应n的平均随机一致性指标RI(random index).

RI是平均一致性指标(通过查RI系数表可得).如果有CI偏差，那么偏差是否在满意的一致性范围，还需要引进平均随机一致性指标RI.RI值见表2.

表2 平均随机一致性指标RI数值

(ⅲ)计算一致性比例CR(consistency ratio)，

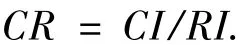
当正互反矩阵满足CR＜0.1时，认为正互反矩阵具有满意的一致性.若检验通过，特征向量(归一化后)即为权向量;反之，当CR≥0.1时，需要对正互反矩阵作适当修正，以保持一定程度的一致性.

2.5 计算各层组合权重

决策最终需要各层元素对总准则的相对权重，以便于对备选方案进行抉择.计算同一层次所有因素对于最高层(总目标)相对重要性的排序权值，称为层次总排序，这一过程是由高层次到低层次逐层进行的.最低层(方案层)得到的层次总排序，就是n个被评价方案的总排序.若上一层A包含m个因素A1，A2，…，Am，其层次总排序权值分别为a1，a2，…，am，下一层次B包含n个因素B1，B2，…，Bn，它们对于因素Aj的层次单排序的权重分别为b1j，b2j，…，bnj(当Bk与Aj无关时，取bkj为0)，此时B层次的总排序由表3给出.若B层次某些因素对于Aj的一致性指标为CIj，相应地平均一致性指标为RIj，则B层次总排序一致性比例为

AHP最终得到方案层各决策方案相对于总目标的权重，并给出这一组合权重所依据整个递阶层次结构所有判断的总一致性指标，从而决策者可以做出决策.

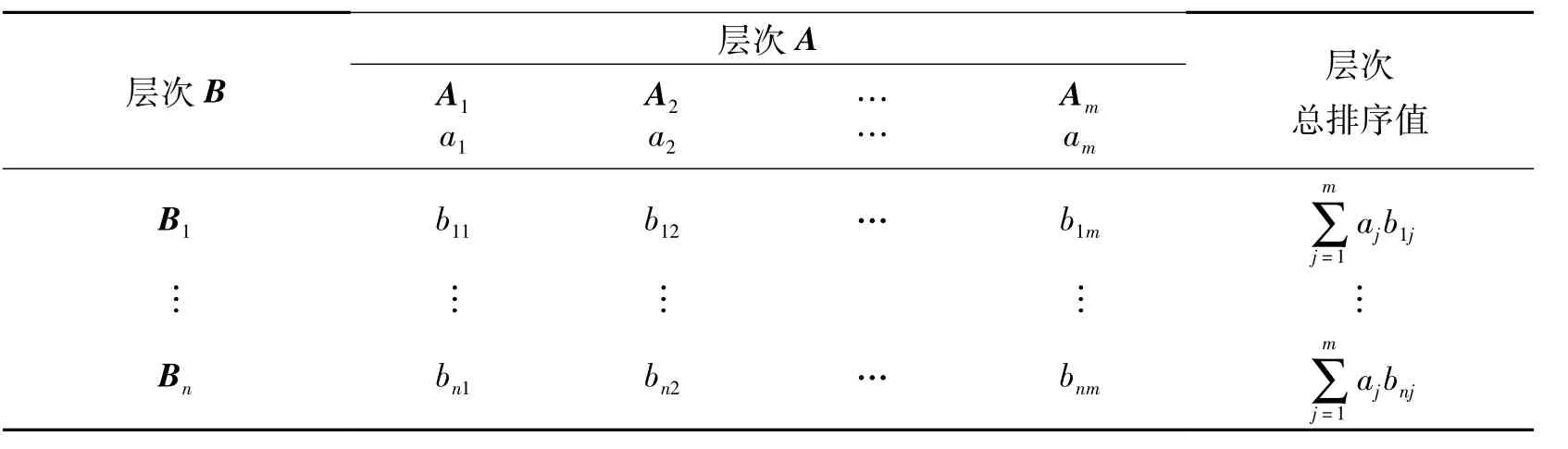
表3 权重合成方法

3 实例分析

欲购买一商品房，现有4个小区A，B，C，D可供选择，主要考察房屋价格、周围环境、学区、单位距离对消费者购买房屋的影响，不考虑其他影响因素.采用AHP层次分析，其层次结构如图1所示.

图1 商品房层次结构

3.1 模型的建立与求解

图1的思维过程可分为以下几个步骤:

(ⅰ)建立层次分析结构模型.将决策问题分解为3个层次，最上层为目标层，即购买房屋，最下层为方案层，有小区A，B，C，D4个供选择的小区，中间层为准则层，有学区、房价、周围环境、单位距离4个准则，各层间的联系用相连的直线表示，而层内各因素基本上相对独立.

(ⅱ)构造成正互反矩阵.通过相互比较确定各准则对于目标的权重，以及各方案对于每一准则的权重.

(ⅲ)将方案层对准则层的权重及准则层对目标层的权重进行综合，最终确定方案层对目标层的权重.

假设要比较某一层n个因素C1，C2，…，Cn对上一层某个因素O的影响，如房屋购买决策问题中比较学区等4个准则在购买房屋这个目标中的重要性.每次取2个因素Ci和Cj，用aij表示Ci和Cj对O的影响之比，全部比较结果可用正互反矩阵

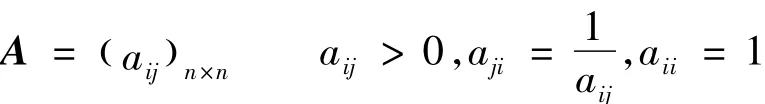
表示，例如用C1，…，C4依次表示学区、房价、周围环境、单位距离4个准则，则得如表4所示的矩阵.

在矩阵Z-C(表4)中，a12=3表示学区C1与房价C2，对选择购买房屋这个目标O的重要性之比为3∶1，a13=2表示学区C1与周围环境C3之比为2∶1，a14=5，a23=2，a34=2.可以得出准则层的重要性排列为C1，C2，C3，C4，即学区因素最重要，房价次之，周围环境再次之，权重最小者为单位距离.

表4 矩阵Z－C

在矩阵C1-P(表5)中，考虑学区这一因素对于方案层的影响程度.由数据可得:a43=2表示学区这一因素对小区D与C的影响之比为2∶1;a12=2表示对小区A与B的影响之比为2∶1;a24=3表示对小区B与D的影响之比为3∶1.由此可知，学区因素对小区的影响为P1，P2，P4，P3，即对小区A影响最大，B次之，D再次之，C最小.

表5 矩阵C1-P

在矩阵C2-P(表6)中，考虑房价这一因素对于方案层的影响程度.由数据可得:a23=5表示房价这一因素对小区B与C的影响之比为5∶1;a34=1/7表示对小区C与D的影响之比为1∶7;a14=1/2表示对小区A与D的影响之比为1∶2;a13=5表示对小区A与C的影响之比为5∶1;a24=1/2表示对小区B与D的影响之比为1∶2.由此可知，房价这一因素对小区的影响为P4，P1，P2，P3，即对小区D影响最大，A次之，B再次之，C最小.

表6 矩阵C2－P

在矩阵C3-P(表7)中，考虑周围环境这一因素对于方案层的影响程度.由数据可得:a23=5表示周围环境因素对小区B与C的影响之比为5∶1;a34=1/7表示对小区C与D的影响之比为1∶7;a14=1/3表示对小区A与D的影响之比为1∶3;a12=3表示对小区A与B的影响之比为3∶1.由此可知，周围环境因素对小区的影响为P4，P1，P2，P3，即对小区D影响最大，A次之，B再次之，C最小.

表7 矩阵C3－P

在矩阵C4-P(表8)中，考虑单位距离这一因素对于方案层的影响程度.由数据可得:a23=1/5表示单位距离因素对小区B与C的影响之比为1∶5;a34=7/1表示对小区C与D的影响之比为7∶1;a14=2/1表示对小区A与D的影响之比为2∶1;a12=1表示对小区A与B的影响之比为1∶1;a13=1/5表示对小区A与C的影响之比为1∶5;a24=2表示对小区B与D的影响之比为2∶1.由此可知，单位距离因素对小区的影响为P3，P1，P2，P4，即对小区C影响最大，A和B次之，D最小.

表8 矩阵C4－P

3.2模型的结果分析

利用单一准则获得的权值和各准则所占比重计算出每个方案总的得分(权数)，如表9所示.

表9 各方案总得分

由表9可知:小区A在总目标中的总得分为0.370 09;小区B在总目标中的总得分为0.246 368;小区C在总目标中的总得分为0.113 891;小区D在总目标中的总得分为0.269 651.

从最终的排序结果可以看出，A，B，C，D这4个小区所占权重的大小为P1＞P2＞P4＞P3，即在购买房屋时，最先考虑的是A小区，其次是B小区，再次是D小区，最后是C小区.AHP定量结果计算出购房时的各种影响因素，以及在评价时决策的权重，为消费者的选择提供了有效且可靠的依据.

［1］ PAULSON D，ZAHIR S.Consequences of Uncertainty in the Analytic Hierarchy Process:Asimulation Approach［J］.European Journal of Operational Research，1995，87(1):45-56.

［2］ 王莲芬，许树柏.层次分析法引论［M］.北京:中国人民大学出版社，1990.

［3］ 徐玖平，吴 巍.多属性决策的理论与方法［M］.北京:清华大学出版社，2006:124.

［4］ MILLER G A.The Magical Number Seven，Plus or Minus Two:Some Limits on Our Capacity for Processing Information［J］.The Psychological Review，1956，63(2):81-97.

［5］ SAATY T L.The Analytic Hierarchy Process［M］.New York:McGraw-Hill，1980.

［6］ SAATY T L.Axiomatic Foundation of the Analytic Hierarchy Process［J］.Management Science，1986，23(7):851-855.

［7］ 蔡 兵.基于修正的BP神经网络的教学质量评估模型［J］.吉首大学学报:自然科学版，2011，32(1):67-70.

(责任编辑 向阳洁)

Some Problems of the AHP and Its Application

XU Yong-lin
(Mathematics and Computer College，North-Western Minorities University，Lanzhou 730030，China)

The analytic hierarchy process(AHP)is widely used in many fields as a classical multi attribute decision-making approach.Through studying the basic theory of AHP，the AHP method was given to determine weight.Method and procedure to solve multi-objective decision by AHP are described.Through the specific examples of property purchase，scientific methods to make consumption decision are presented.

analytic hierarchy process;judgment matrix;scale;multi-objective decision making;weight

C934

A

10.3969/j.issn.1007-2985.2013.02.003

1007-2985(2013)02-0012-07

2012-12-11

国家自然科学基金资助项目(11161041);2011—2012年度校级中青年科研基金项目(12XB39);2013中央

高校基本科研业务费专项资金项目(31920130006)

徐永琳(1969-)，女，甘肃夏河人，西北民族大学数学与计算机科学学院副教授，硕士，主要从事数学课程

与教学论、运筹学研究.