矿用电机车手轮闸瓦制动连杆机构稳健设计＊

文泽军，王兆波，岳文辉，杨书仪，刘爱军

（湖南科技大学机械设备健康维护湖南省重点实验室，湖南湘潭 411201）

矿用电机车手轮闸瓦制动连杆机构稳健设计＊

文泽军，王兆波，岳文辉，杨书仪，刘爱军

（湖南科技大学机械设备健康维护湖南省重点实验室，湖南湘潭 411201）

以矿用电机车手轮闸瓦制动连杆机构为研究对象，应用遗传算法和蒙特卡洛模拟法对其参数进行稳健设计与优化.首先，对矿用电机车手轮闸瓦制动连杆机构的运动过程进行分析，建立理想状况下的闸瓦制动连杆机构运动学模型.然后，考虑转动副间隙对该机构进行运动学分析，建立计入转动副模型的闸瓦制动连杆机构运动学模型.最后，以机构杆长为设计变量，以转动副间隙、间隙副接触角和杆件加工误差为噪声因素，建立以闸瓦制动距离误差均值和标准差最小化为目标的矿用电机车手轮闸瓦制动连杆机构参数稳健设计优化模型，并运用遗传算法和蒙特卡洛模拟法对参数进行稳健设计与优化.结果表明，闸瓦制动连杆机构制动距离的误差均值减小了15.4%，标准差降低了28.6%.在不提高连杆制造精度的前提下，能显著降低闸瓦制动过程的不确定性，对提高矿用电机车手轮闸瓦制动连杆机构的设计质量具有重要意义.

稳健设计；连杆机构；制动系统；矿用电机车

1 手轮闸瓦制动连杆机构运动学建模

1.1 闸瓦制动连杆机构描述

如图1所示，司机在驾驶室内通过控制手轮1带动均衡杆2和拉杆3，将力传递到制动杆4上，最终使闸瓦压紧车轮实现制动.

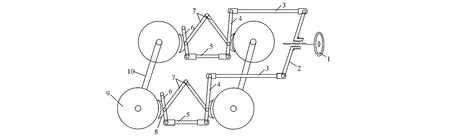
图1 矿用电机车手轮闸瓦制动原理

1.2 机构运动学分析与建模

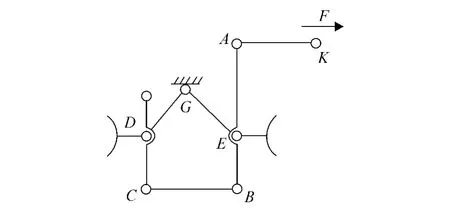
图2 连杆机构简图

对图1所示的矿用电机车手轮闸瓦制动连杆机构实施简化，如图2所示.图2中KA为拉杆，AB为前制动杆，BC为传动杆，CD为后制动杆，GD与GE为机架杆，K点为拉杆与均衡杆的衔接点；A，B，C，D，E，K为销轴连接，其中D，E，K3处的销轴与车身相连接，在连杆运动过程中仅考虑A，B，C3处销轴的转动副.

设车轨前进方向为x轴的正方向，后闸瓦与车轮接触点垂直于轮轨方向为y轴正方向，建立坐标系，如图3所示.拉杆在力F的作用下向右移动，S表示K点与D处销轴沿x方向的水平距离，通过比较K点制动前后其距离变化ΔS可以得到手轮转角与闸瓦车轮间距的关系.

矿用电机车手轮闸瓦制动机构的运动过程如图4所示，虚线A′B′C′D表示连杆机构制动前的位置.

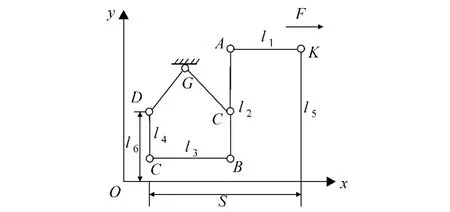
图3 连杆机构示意

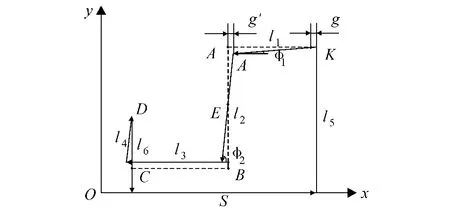
图4 连杆机构运动示意

设手轮螺距为u，转角为θ，闸瓦与车轮的间距为t，则可以推导出闸瓦制动距离t0与手轮转角θ运动关系式.由K点制动前后的距离变化ΔS（即均衡杆沿x方向移动距离变化）可以计算出手轮转角θ.设ΔS＝g，A点制动前后的沿x方向变化为g′，则转角θ与g的关系为后制动杆l4与车轮间隙t的关系为

g′与φ2角的关系为

转角偏差为1°左右，取g≈g′，由（1）至（3）式，推导得闸瓦制动距离t0与手轮转角θ关系式，即理想状况下的闸瓦制动连杆机构运动学模型为

2 计入转动副模型的手轮闸瓦制动连杆机构运动学建模

2.1 转动副模型

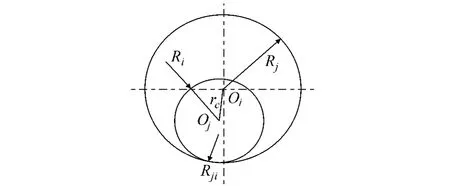
图5 转动副模型

图5示出转动副模型.由于孔销的制造误差，孔销会产生偏心距rc，设销轴和轴套半径为Ri和Rj，因此转动副间隙为rc＝Ri－Rj.设转动副符合连续接触假设，即孔和销始终保持接触，不会出现轴悬浮在孔中的情况，因孔销的尺寸均服从正态分布［8］，故显然rc亦服从正态分布.由于无法确定转动副中轴孔的接触位置，因此接触角α可视为在［0，2π］之间服从均匀分布［8］.

2.2 机构运动学分析与建模

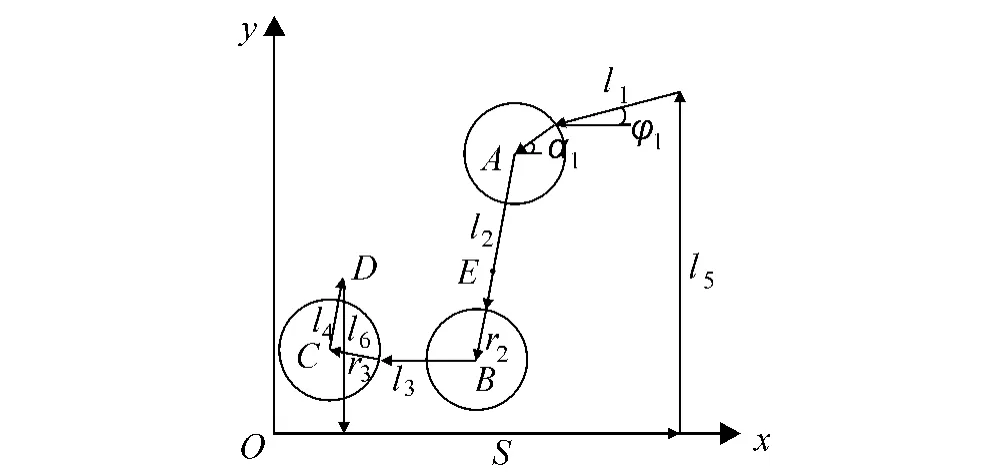
图6 计入转动副模型的连杆机构简图

将转动副模型引入到矿用电机车手轮闸瓦制动连杆机构中，那么计入转动副模型的连杆机构运动可简化如图6所示.

该机构含有3个转动副，引入连续接触模型：它将间隙视为一无质量的假想杆，其长度等于r，杆件方向由销轴和轴套的接触点位置决定，方向是变化的，可用接触角α表示.

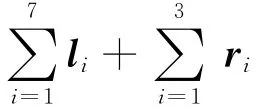
其中：li为机构的杆长；φi为杆矢量，li方向与x轴正方向夹角；ri为转动副间隙半径；αi为间隙矢量即转动副接触角，表示ri正方向与x轴正方向夹角.

将 （5）式展开，得到该连杆机构的运动方程：

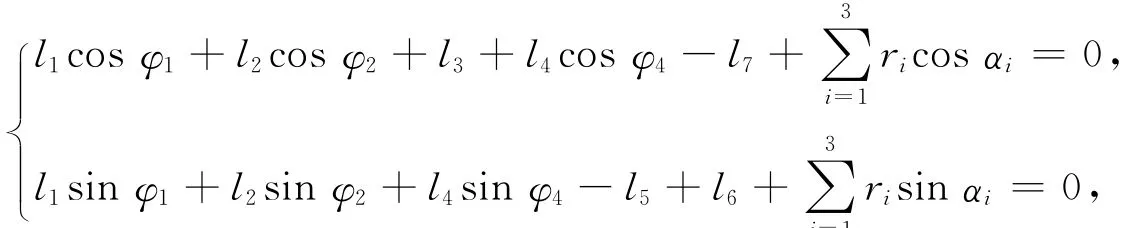
其中φ3＝0°，φ4－φ2＝180°，l5－l6＝l2－l4.消去φ1，则可得到制动后K点沿x方向的距离S与l2杆和x轴正方向夹角φ2的关系：

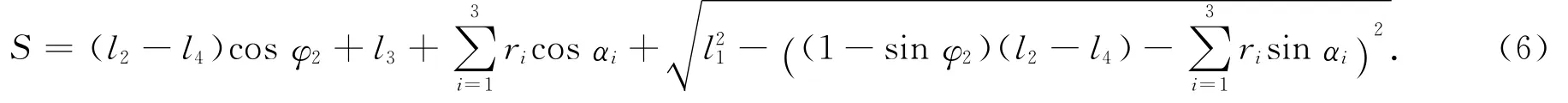
因ΔS＝S－l1－l3＝g，故由（6）式可以得到闸瓦的制动距离t与手轮转角θ的关系，即计入转动副模型后的闸瓦制动连杆机构运动学模型为

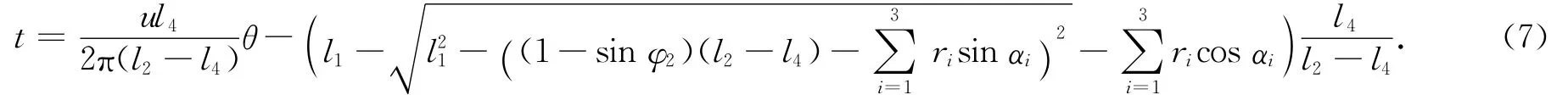
2.3 间隙副接触角

根据连续接触理论，目前对于连杆机构间隙副接触角的变化范围都设定在［0，2π］间服从均匀分布，为了更接近实际情况同时缩小转动副接触角的变化范围，对连杆机构的传动过程进行模拟.

如图7所示，设A处为前制动杆孔与连杆销配合，B处为前制动杆孔与连杆销配合，C处为连杆销与后制动杆孔配合，3处运动趋势可做如下假设：φi为连杆机构的位置角，ri为间隙，αi为转动副接触角.根据机构的运动方向可以将接触角的均匀分布区间进行模拟：拉杆向右移动，对A处的接触角有拉杆销为主动件则其变化范围为－90°≤α1≤90°；对B，C2处的接触角，连杆向左移动，可得其变化范围为0°≤α2≤180°，0°≤≤180°.α1，α2，α3分别表示A，B，C3处销轴的转动副接触角，其中＝α3－π，则180°≤α3≤360°.

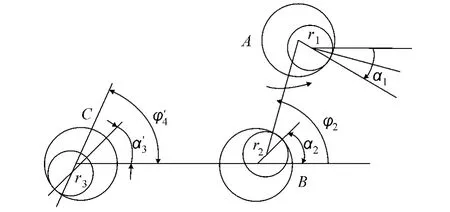
图7 接触角假设

3 手轮闸瓦制动连杆机构参数稳健优化设计

3.1 闸瓦制动连杆机构实例描述

以某公司生产的某型号8t矿用电机车为研究对象，杆长l1＝910mm，l2＝795mm，l3＝280mm，l4＝210mm.闸瓦与车轮间隙t的可调节范围为3～5mm，设闸瓦间隙为4mm，那么可得到制动前后拉杆的移动距离g和制动杆在水平方向上的夹角φ2变化范围为0≤g′≈g≤11.7mm，88.9°≤φ2≤90°.

销轴与轴孔的基本尺寸为φ＝22mm，采用间隙配合H11／h11，经查表，知轴孔公差为公差为，视平均间隙为正态分布，那么其平均间隙为

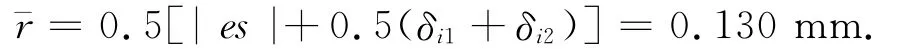
尺寸分布误差一般服从正态分布，由3σ原则可以确定其标准差为

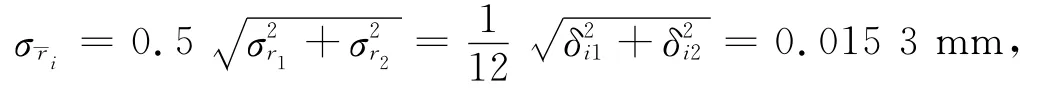
其中δi1与δi2分别为孔销尺寸的公差带，es为销轴尺寸的上偏差.

在闸瓦制动过程中，手轮每转180°均匀取6个点，闸瓦制动距离的误差由下式计算：

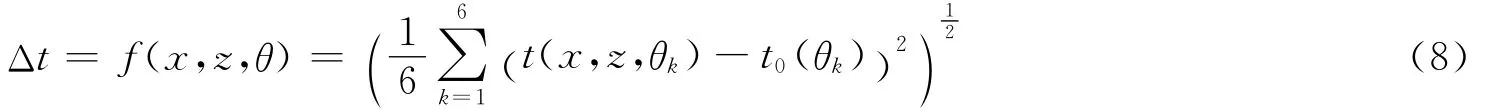
其中：x＝（l1，l2，l3，l4）T＝（x1，x2，x3，x4）T为设计变量；z＝（Δl1，Δl2，Δl3，Δl4，r1，r2，r3，α1，α2，α3）T＝（z1，z2，...，z10）T；t按（7）式计算；t0按（4）式计算.为了比较稳健设计的结果，采取不增加机构各杆长制造精度的原则，即Δl1，Δl2，Δl3，Δl4取值与原方案相同，各参数分布情况如表1所示.

表1 设计变量与噪声因素的分布参数

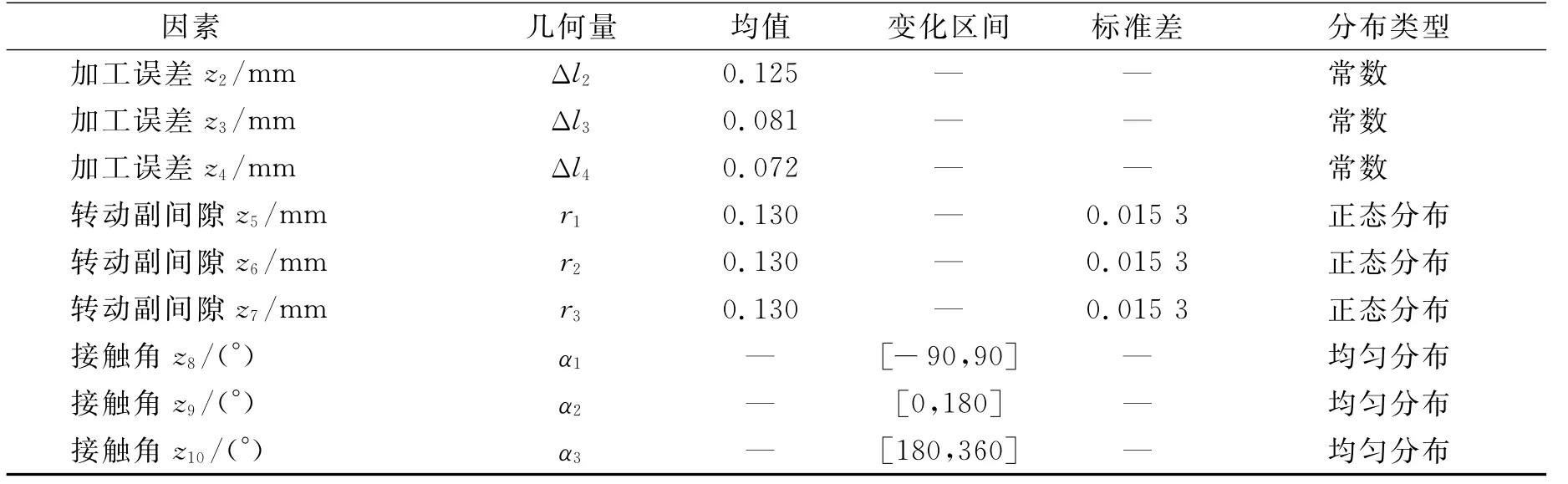
续表

3.2 稳健设计优化模型

由（8）式，设Δt的均值为μf，标准差为σf，根据稳健设计原理，Δt的均值与标准差均具有望小特性，综合以上分析，闸瓦制动距离的稳健优化设计模型可建立为：

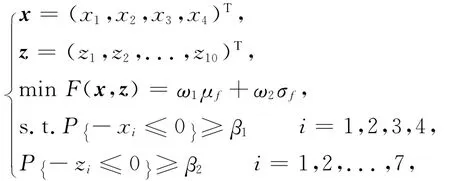
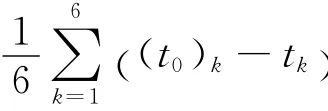
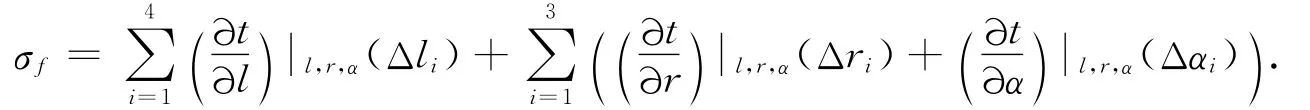
目标函数F由2部分组成：第一部分误差均值的作用是使闸瓦制动距离误差均值尽量接近理想运动值，以期望提高闸瓦制动连杆机构的运动精度；第二部分标准差的作用是尽量减少闸瓦制动距离误差的标准差，以期望减少闸瓦制动过程的不确定性.β为约束条件应该满足的概率值，β1＝β2＝1，权重系数ω1和ω2一般由设计者决定.

3.3 优化结果与分析

采用遗传算法求解上述闸瓦制动距离的稳健优化设计模型.各设计变量初值与噪声因素的分布参数选取见表1.根据参考文献［6］选取权重系数，取ω1＝ω2＝100，设置种群数为40，交叉率为0.9，变异率为0.3.遗传算法的基本流程如图8所示.

经过2 000次遗传进化，得到稳健设计结果，如表2所示.

表2 参数稳健设计结果比较 mm

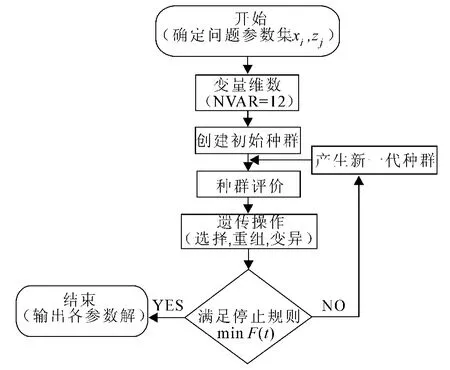
图8 遗传算法流程

为了分析稳健优化设计结果，从2个方面对优化前后的解进行比较.

（1）优化前后闸瓦制动距离t的绝对误差比较.按表2的参数通过5万次蒙塔卡洛模拟法分别求出优化后和优化前闸瓦制动距离误差均值，得到各手轮转角θm（m＝1，2，...，6）处的制动距离误差均值，然后求得各θm处2种方案与理想值的绝对误差.计算结果如图9所示.通过比较可知闸瓦制动连杆机构制动距离误差的均值减小了15.4%，优化后的矿用电机车手轮闸瓦制动连杆机构的运动特性更加接近理想状态.

（2）优化前后闸瓦制动距离t的标准差比较.按表2的参数通过5万次蒙特卡洛模拟法分别求出稳健优化解和各θm处制动距离的标准差.计算结果如图10所示.通过比较可知，闸瓦制动连杆机构闸瓦制动距离误差的标准差降低了28.6%，该标准差越小闸瓦制动距离t的随机波动量越小，即连杆机构制动性能的稳健性越好.

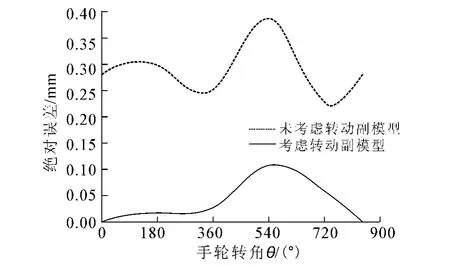
图9 闸瓦制动距离绝对误差比较

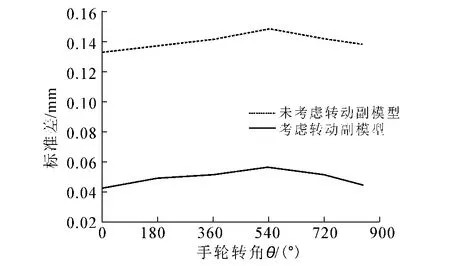
图10 闸瓦制动距离标准差比较

4 结语

（1）通过分析闸瓦制动连杆机构的运动过程，建立了理想状态下闸瓦制动连杆机构的运动学模型；考虑转动副间隙的影响，建立了计入转动副模型的闸瓦制动连杆机构运动学模型；为了更加符合实际情况，对转动副接触角进行模拟，缩小了转动副接触角的变化范围.

（2）考虑闸瓦制动连杆机构的杆件制造误差和转动副间隙、转动副接触角的影响，建立了以闸瓦制动距离误差均值和标准差最小化为目标的矿用电机车手轮闸瓦制动连杆机构参数稳健设计优化模型，运用遗传算法和蒙特卡洛模拟法对参数进行稳健设计与优化.结果表明，闸瓦制动连杆机构制动距离的误差均值减小了15.4%，标准差降低了28.6%.

在不提高制造精度的前提下，通过稳健设计有效降低了闸瓦制动距离的不确定性，对提高矿用电机车手轮闸瓦制动连杆机构的设计质量具有重要意义.

［1］ 任丕顺.基于模糊理论的平面连杆机构稳健设计方法［J］.湖南文理学院学报：自然科学版，2003，15（4）：56－59.

［2］ 林建龙，罗智文，张 力.电脑刺绣机针杆机构位置精度分析［J］.纺织学报，2010，32（7）：131－134.

［3］ 谭晓兰，韩建友，何广平.连杆机构稳健设计一般原理与方法的研究［J］.机械设计与研究，2006，22（4）：24－27.

［4］ 张 蕾，张文明，申焱华.考虑间隙影响的汽车转向机构稳健优化设计［J］.农业机械学报，2007，38（1）：30－32.

［5］ HECTOR ALLENDE，DANIELA BRAVO，ENRIQUE CANESSA.Robust Design in Multivariate System Using Genetic Algorithms［J］.Quality ＆Quantity，2010，44：315－332.

［6］ 郭惠昕.刺绣机含间隙针杆机构的运动稳健性分析与优化设计［J］.纺织学报，2011，32（11）：131－136.

［7］ 郭惠昕，岳文辉.含间隙平面连杆机构运动精度的稳健优化设计［J］.机械工程学报，2012，48（3）：75－81.

［8］ 宋 黎，曹惟庆，褚金奎.间隙曲柄滑块机构运动误差分析的模拟实验修正法［J］.机械设计，1999，4（4）：37－40.

（责任编辑 向阳洁）

Robust Design for Handwheel Shoe Brake Linkage of Electric Mine Locomotive

WEN Ze－jun，WANG Zhao－bo，YUE Wen－hui，YANG Shu－yi，LIU Ai－jun
（Hunan Provincial Key Laboratory of Health Maintenance for Mechanical Equipment，Hunan University of Science and Technology，Xiangtan 411201，China）

A robust parameter design and optimization of handwheel shoe brake linkage for electric mine locomotive are studied，with genetic algorithm（GA）and Monte Carlo simulation used.Firstly，the kinematic model of linkage is established while the braking process of handwheel shoe brake linkage is analyzed.Secondly，the kinematical model of handwheel shoe brake linkage for electric mine locomotive is established based on the revolving pair clearance model.Finally，with the objective to satisfy the lowest mean error and standard deviation of shoe brake distance，taking the linkage length for the design variables and the revolving pair clearance and contact angle and machining error for noise factors，the model of robust parameter design and optimization for handwheel shoe brake linkage of mine electric locomotive is established，and the parameters are optimized.The result shows that the absolute error of shoe brake distance reduced by 15.4%，and the standard deviation of shoe brake distance reduced by 28.6%.The uncertainty of shoe brake process can be significantly reduced without raising the manufacturing precision of linkage.It has important significance in the design quality of handwheel shoe brake linkage.

robust design；linkage；braking system；electric mine locomotive

TP028.8

A

10.3969／j.issn.1007－2985.2013.03.011

1007－2985（2013）03－0049－06

在矿用电机车手轮闸瓦制动连杆机构中，转动副连接着拉杆、制动杆和传动杆并允许相互间有相对运动，故转动副需要有一定的间隙，连杆机构间的多个转动副间隙导致闸瓦制动存在不确定性误差.近年来，相关学者围绕连杆机构不确定性分析与参数稳健设计进行了如下研究：任丕顺［1］基于模糊理论建立了考虑制造误差的平面连杆机构稳健优化模型；林建龙等［2］提出了考虑电脑刺绣机针杆制造误差对该机构位置精度的分析方法.以上研究工作着重考虑了制造误差对连杆机构位置精度的影响.谭晓兰等［3］综合分析了杆件尺寸和运动副间隙的随机变化并提出了机构稳健设计的一般方法；张蕾等［4］提出了含间隙汽车转向梯形机构的稳健优化模型；Hector等［5］在多变量系统中考虑噪声因素的影响应用遗传算法对其进行优化设计；郭惠昕［6］建立了刺绣针杆机构杆长误差和运动副间隙对针杆位移精度影响的连杆机构稳健优化设计方法；郭惠昕等［7］综合分析了3种含杆长制造误差和运动副间隙影响的连杆机构模型.这些研究同时考虑了连杆机构杆长制造误差和运动副间隙的影响，有效地降低了连杆机构运动的不确定性，显著提高了连杆机构的运动精度.

笔者在上述研究工作的基础上，以矿用电机车手轮闸瓦制动连杆机构为研究对象，首先，拟对矿用电机车手轮闸瓦制动连杆机构的运动过程进行分析，建立理想状况下的闸瓦制动连杆机构运动学模型.然后，考虑转动副间隙对该机构进行运动学分析，建立计入转动副模型的闸瓦制动连杆机构运动学模型.最后，以机构杆长为设计变量，以转动副间隙、间隙副接触角和杆件加工误差为噪声因素，建立以闸瓦制动距离误差均值和标准差最小化为目标的矿用电机车手轮闸瓦制动连杆机构参数稳健设计优化模型，并运用遗传算法和蒙特卡洛模拟法对参数进行稳健设计与优化.

2013－03－05

湖南省产学研结合技术创新工程计划项目（2010XK6066）；国家自然科学基金资助项目（51075141）；湖南省教育厅科学研究项目（11C0531）；湖南省自然科学省市联合基金重点项目（11JJ8005）

文泽军（1966－），男，湖南湘乡人，湖南科技大学副教授，博士，硕士研究生导师，主要从事制造系统质量控制、制造过程监测与控制、面向产品制造／装配过程的稳健设计研究.