Clifford分析中Isotonic函数向量的一类线性边值问题*
2013-09-11鄢盛勇
鄢盛勇
(成都师范学院数学系,四川成都 611130)
Clifford分析中Isotonic函数向量的一类线性边值问题*
鄢盛勇
(成都师范学院数学系,四川成都 611130)
研究了Clifford分析中Isotonic函数向量的一类带位移、带共轭的线性边值问题.通过设计积分算子将边值问题转化为积分方程,借助积分方程理论和不动点原理证明了问题解的存在性,并给出解的积分表达式.
Clifford分析;Isotonic函数向量;线性边值问题
Clifford分析是近代分析的重要分支,它有非常重要的理论意义和应用价值,如在Maxwell方程、Yang-Mill场理论以及量子力学等方面都应用了它的一些结论[1].文献[2-7]利用Plemelj公式解决了高维空间中某些边值问题.文献[8-12]研究了定义于R2m中子区域而取值于复Clifford代数Cm且满足+=0的Isotonic函数,得到其柯西积分公式、Plemelj公式,并建立其与多复变全纯函数、Hermitean单演函数、双正则函数的紧密联系.文献[12]还解决了Isotonic函数的线性边值问题.在此基础上,笔者讨论了Isotonic函数向量的一类带位移带共轭的线性边值问题

其中α(x)是∂Ω到自身的同构映射,证明了其解的存在唯一性,并给出解的积分表达式.
1 预备知识与记号


2 Isotonic函数与Isotonic柯西型积分


3 问题的的解法
Ω,∂Ω如前所述,A(x),B(x),C(x),D(x)∈Hβ(∂Ω,Cm)为给定的p维函数向量,α(x)为∂Ω上的Haseman位移[13],现要找在Ω±内Isotonic的,在上连续,且满足边界条件(1)和Φ-(∞)=0的p维函数向量Φ(x).称此边值问题为问题LR.
首先将此边值问题转化为积分方程.将(2),(3)式代入(1)式,得

这样求解边值问题LR转化为了求解积分方程组(4).
定理3 对任意函数g∈(∂Ω,C2m),有

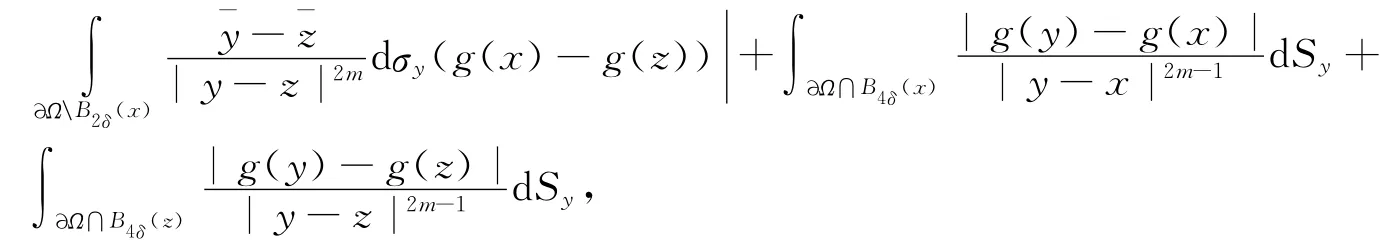
其中Bδ(x)表示中心在x且半径为δ的超球.当y∈∂Ω\B2δ(x)时,有2δ≤|y-x|≤|y-z|+δ,故|z-y|≥δ,|y-x|≤2|z-y|,|z-y|-1≤2|y-x|-1,从而有



所以当γ<1时,算子Q是Hβ(∂Ω,Cm)到自身的压缩映射.由不动点定理可知,存在唯一一个属于Hβ(∂Ω,Cm)的p维函数向量F0满足奇异积分方程(4),因此问题LR存在唯一的解Φ(x)(如(5)式所示),显然满足Φ-(∞)=0.由文献[11]知Φ(x)的每一个分量函数在内连续,从而Φ(x)在内连续.
[1] BRACKX F,DELANGHE R,SOMMEN F.Clifford Analysis[M].Pitman,London:Res.Notes Math.,1982:76.
[2] HUANG Sha.Nonlinear Boundary Value Problem for Biregular Functions in Clifford Analysis[J].Science in China Ser.A,1996,39(3):1 152-1 164.
[3] QIAO Yu-ying.A Boundary Value Problem for Hypermonogenic Functions in Clifford Analysis[J].Science in China Ser.A.Mathematics,2005,48:324-332.
[4] 谢永红,杨贺菊.Clifford分析中无界域上向量值函数的非线性边值问题[J].高校应用数学学报,2010,25(2):163-171.
[5] 鄢盛勇.四元数分析中一类带共轭带位移的边值问题[J].广西民族大学学报:自然科学版,2011,17(3):49-53.
[6] 鄢盛勇.Clifford分析中无界域上正则函数的非线性边值问题[J].怀化学院学报,2011,30(5):1-4.
[7] 鄢盛勇.四元数分析中正则函数的非线性带位移边值问题[J].纯粹数学与应用数学,2012,28(4):475-482.
[9] ABREU-BLAYA R,BORY-REYES J.A Martinelli-Bochner Formula on Fractal Domains[J].Arch.Math.,2009,92:335-343.
[10] ABREU-BLAYA R,BORY-REYES J,D,et al.A Holomorphic Extension Theorems Using Clifford A nalysis[J].Complex Anal.Oper.Theory,2011,5:113-130.
[11] 库 敏,杜金元,王道顺.Clifford分析中Isotonic柯西型积分的边界性质[J].数学学报,2011,54(2):177-186.
[12] 李 婧.复Clifford分析中Isotonic函数的性质及其边值问题[D].石家庄:河北师范大学,2010.
[13] 路见可.解析函数边值问题教程[M].武汉:武汉大学出版社,2009.
(责任编辑 向阳洁)
A Class of Linear Boundary Value Problem for Isotonic Functional Vector in Clifford Analysis
YAN Sheng-yong
(Department of Mathematics,Chengdu Normal University,Chengdu 611130,China)
This paper discusses a class of linear boundary value problem with conjugate value and a kind of shift for isotonic functional vector in Clifford analysis.Firstly,the author gives some integral operators and tansform the problem into an integral equation problem.Applying the integral equation method and Schauder fixed-point theorem,the author proves the existence of the solution for the problem,and gives the integral representation of solution.
Clifford analysis;isotonic functional vector;linear boundary value problem
O175.5
A
10.3969/j.issn.1007-2985.2013.02.002
1007-2985(2013)02-0007-05
2012-12-02
教育部科学技术研究重点资助项目(212147)
鄢盛勇(1975-),男,四川井研人,成都师范学院数学系副教授,硕士,主要从事函数论与偏微分方程的边值问题研究.
