车辆荷载作用下大跨旧桥动力可靠度研究

孟阳君，周先雁

(中南林业科技大学，长沙 410004)

1 结构动力可靠度分析及程序设计

结构动力可靠度指结构在随机作用下、预定使用期内、规定使用条件下结构不发生失效的概率。动力可靠度理论是近年发展的随机振动理论分支。其涉及问题难度较大，诸多基本问题尚未解决。而动力可靠度研究方法有首超破坏机制与疲劳破坏机制。

随机过程x(t)与某一界限x=b交叉次数统计是首超破坏机制动力可靠性分析基础。该问题由赖斯于1944年首次提出。

考虑x(t)以正斜率(dx/dt＞0)与界限x=b交叉，有:

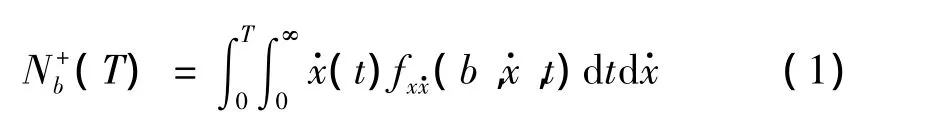
考虑x(t)的负斜率(dx/dt＜0)交叉问题，有:

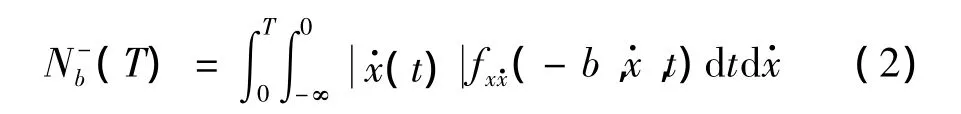
计算首次超越破坏机制的动力可靠性问题关健为计算首次超越时间Tf的概率分布函数。但即使最简单情况-受平稳白噪声荷载作用的单自由度体系动力反应过程，其首次超越时间Tf的精确解尚未找到，故退而寻找近似解，最简单、最重要的当属泊松过程法。

对双侧界限x=-b2，x=b1，动力可靠度Ps定义为:

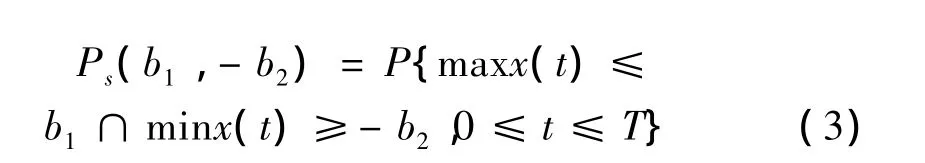
基于平稳随机过程，多自由度体系泊松过程法涉及的交叉次数期望值计算远比单自由度体系复杂，因此采用振型分解法(其优点为在正交阻尼条件下，可将多自由度体系与无限自由度体系化为一系列广义单自由度体系分析)。先需对结构进行随机反应分析。动力方程为:

用阵型分解法将式(4)变换为关于广义坐标振动方程，令:

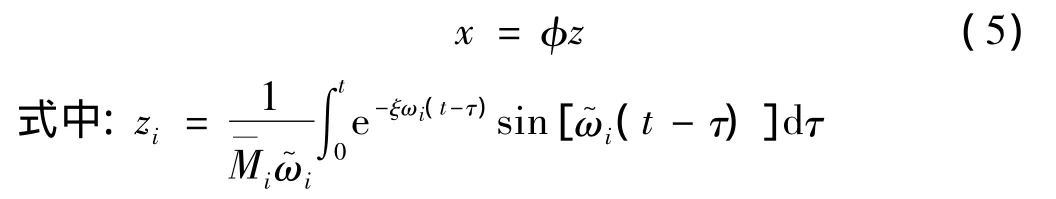
通过变形可得结构相应的广义刚度、广义质量、广义荷载等参数，具体表达式略。据随机过程理论，结构广义坐标zi，zj间相关函数为:

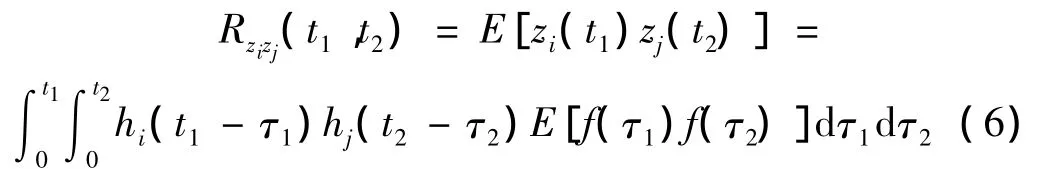
式中:hi(t)为单位脉冲响应函数。

通过整理分析得:

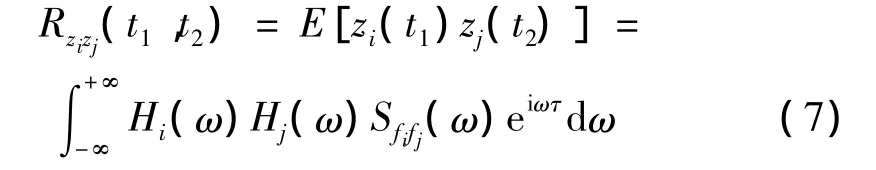
式中:Hi(ω)为传递函数或频率响应函数，与hi(t)为一对傅氏变换。

由此得结构广义坐标与广义力间互功率谱为:

由分析得多自由度第i质点位移功率谱Sxi与方差为:

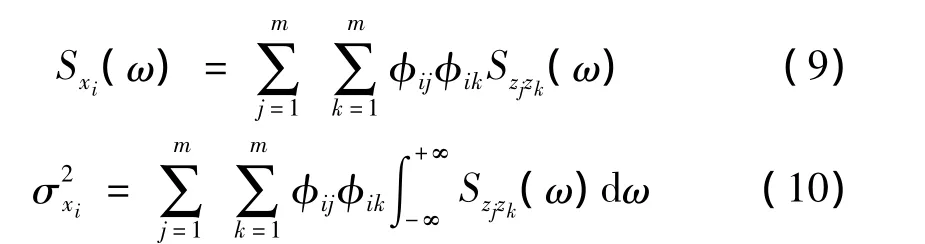
结构振动第j阵型为:

多自由度第i质点速度方差与加速度方差分别为:

求出各参数后，即可对结构动力可靠度进行求解:

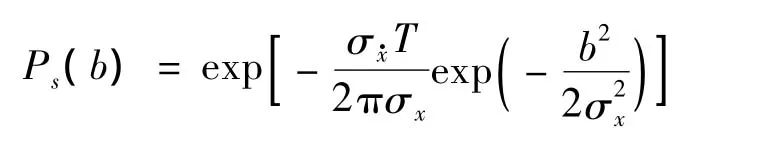
基于以上理论，采用Fortran语言自编《PMDK动力可靠度分析程序》，分析流程见图1。

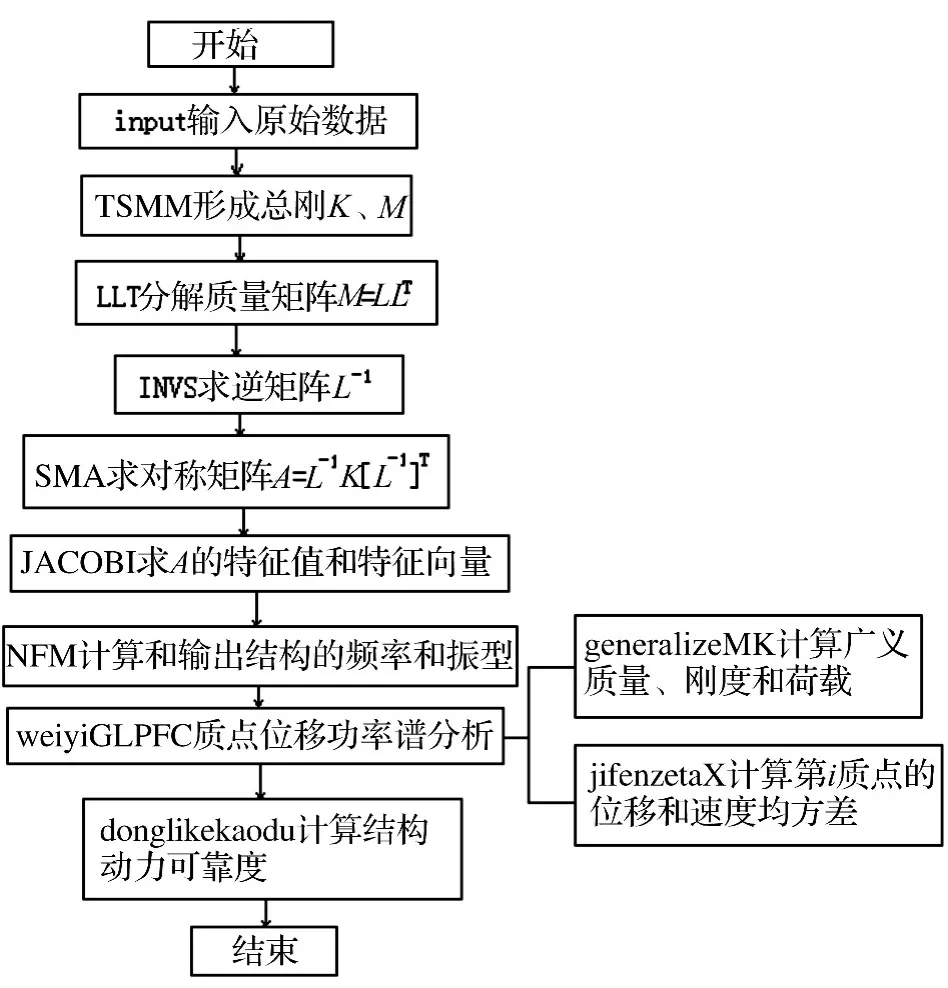
图1 PMDK动力可靠度分析程序流程图Fig.1 Program flowchart for PMDK dynamic reliability analysis

2 车辆荷载分布概率模型

公路桥梁动力可靠度分析重点为确定荷载(效应)的统计特性。常采用对数正态分布或反正态分布对车辆荷载分布进行拟合检验。正、反两种分布均属单峰型分布，而实测车辆荷载却出现多峰型分布特点，采用正、反两种分布较难获得满意结果且不会通过K-S检验。为准确描述实际存在的多峰车辆荷载分布，本文用极值Ⅰ型、正态分布、对数正态分布函数的加权和各一拟合车辆荷载多峰分布累积分布函数。令f(x)为拟合所得密度函数，则有:

据已有数据，用参数拟合方法，设该车辆荷载多峰分布累计分布函数为:

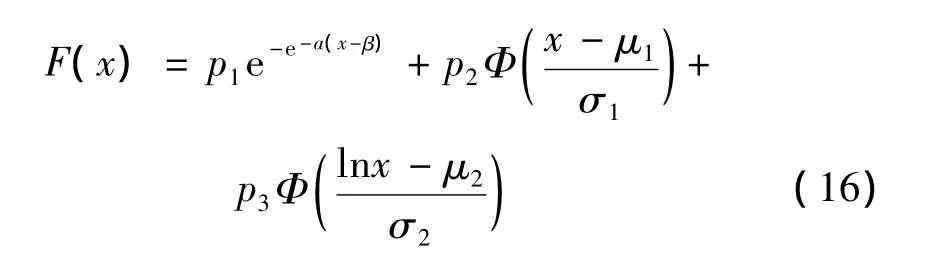
式中:p1，p2，p3分别为极值Ⅰ型分布函数概率、正态分布函数概率及对数正态分布函数概率，p1+p2+p3=1;α，β为极值Ⅰ型分布函数参数;μ1，σ1为正态分布函数期望值、标准差;μ2，σ2为对数正态分布函数期望值、标准差。

求解以上参数可采用无约束规划求解方法，具体为:设实际累计分布函数与拟合累计分布函数满足:

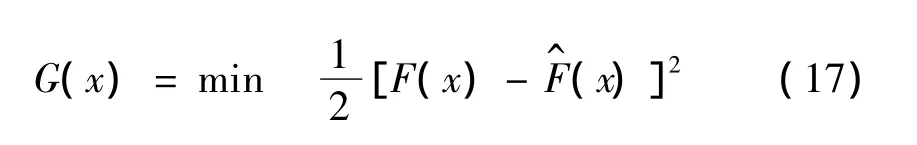
式(17)为无约束非线性规划问题，通常采用牛顿法及变形方法、遗传算法、神经网络、Levenbery-Marquardt法(简称LM法)等计算。本文采用LM法。据多元函数取极值必要条件，式(17)的无约束规划问题等价于求解:

式中:θ=(p1，p2，p3，μ1，σ1，μ2，σ2，α，β)为未知参数向量。

LM法具体计算步骤如下:

(1)设初值θ0;

(2)对第k次迭代解θk，确定搜索增量dk，令:θk+1= θk+dk，若 θk+1符合给定的迭代终止原则，停止迭代，最优解θ'=θk+1;否则转(2)。

将f(θ)在 θk点做泰勒展开，保留到一次项，整理得:

式中:Df(θ)为雅克比矩阵:

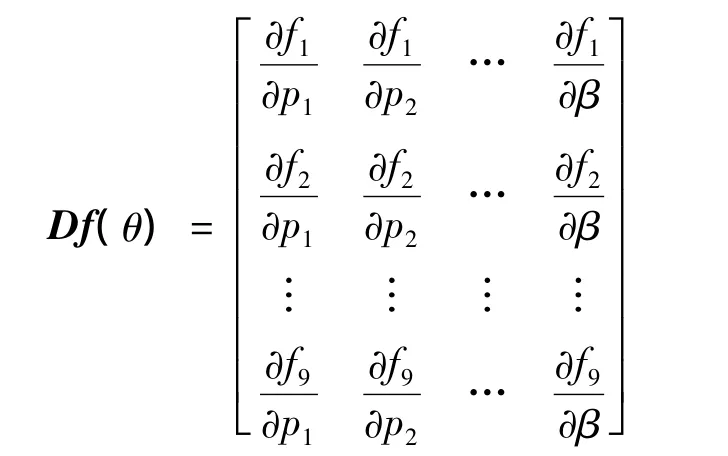
为防止迭代矩阵Df(θk)TDf(θk)奇异或病态，LM法将式(19)修改为:

其中:I为单位阵，μk为阻尼因子，一般取0.01 ～0.0001之间。

通常可用‖Δθk‖＜ε或‖J(θk)‖＜δ作为LM法的终止迭代准则，其中δ，ε为给定精度要求。也可确定最大迭代次数M作为终止条件。

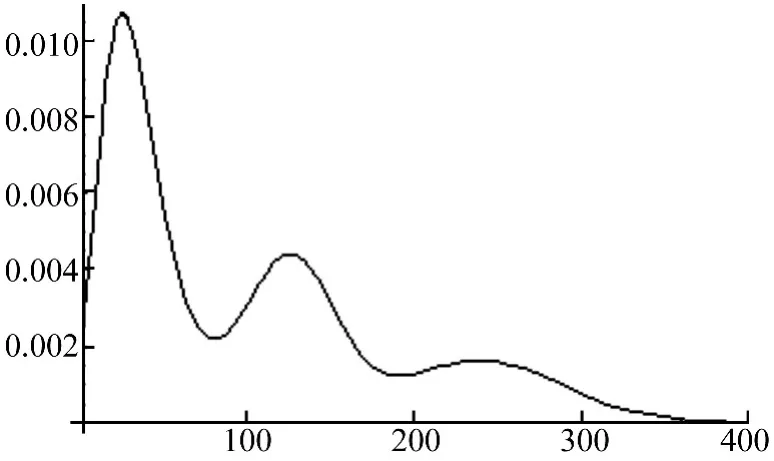
图2 车辆荷载概率分布Fig.2 Vehicular load probability distribution

据观测数据，采用上述求解方法，得各参数分别为:α =0.056 8，β =24.17，μ1=125.24 kN，σ1=26.90 kN，μ2=5.455 856 kN，σ2=0.207 89 kN，p1=0.512，p2=0.283，p3=0.205，概率分布见图 2。

3 试验分析

3.1 项目简介

某桥为预应力混凝土连续梁桥，跨径80+116+80(m)，已安全运营20余年。该桥设计荷载为公路Ⅱ级。由于重车激增，主体结构暴露出不良病害。为确保大桥结构安全与长期使用性能，对该桥进行外观检测及静、动载荷载试验。

3.2 试验及理论分析

300 kN载重试验车，分别以10 km/h、20 km/h、30 km/h、40 km/h、50 km/h五个不同车速沿桥中心线匀速行驶，测得中跨跨中部分加速度响应及动应变时程响应曲线见图3、图4。

图3 中跨跨中动应变时程响应图(V=30 km/h)Fig.3 Dynamic strain Time-History response at center of midspan

图4 边跨跨中动应变时程响应图(V=40 km/h)Fig.4 Dynamic strain Time-History response at center of side span

由图3、图4得各车速的实测冲击系数见表1。由表1看出，冲击系数与车速有关，且呈非线性关系。v=40 km/h所得最大冲击系数较按规范［2］计算值1.292 2大 0.087 8。对加速度响应信号进行分析，得该桥(旧桥)阻尼系数为ξb=0.04。通过参数分析程序可得该桥截面抗弯惯性矩I、截面面积A等值。限于篇幅，仅列出中跨跨中截面I的特征参数见表1。据本文车辆荷载分布概率模型，计算得车辆荷载功率谱密度函数为:

表1 跨中实测冲击系数及中跨跨中I值一览表Tab.1 Actual impact coefficient and inertia moment at center of midspan

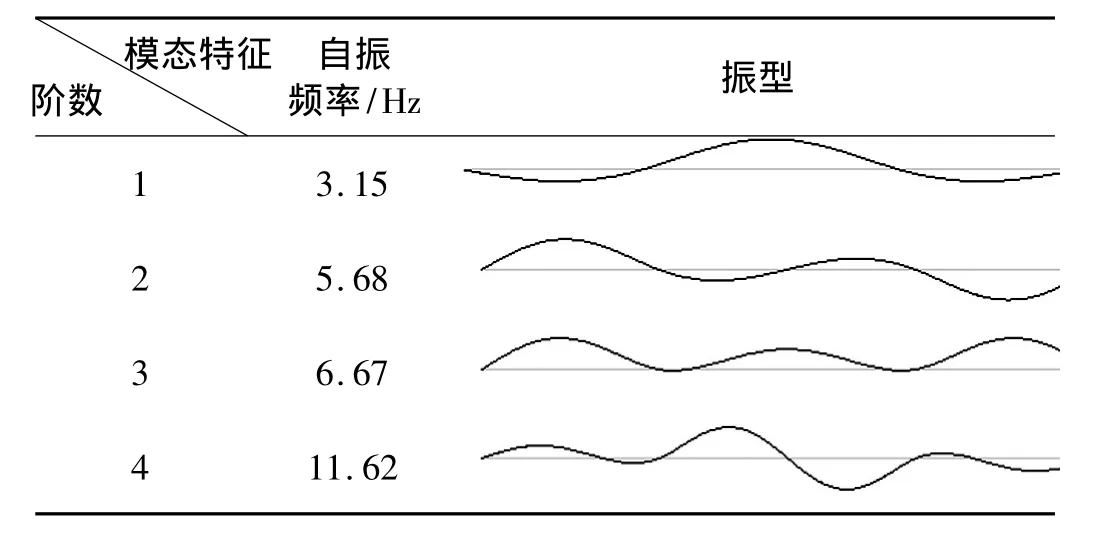
表2 大桥自振频率及振型一览表Tab.2 Natural frequency of vibration and modal for the bridge

对结构进行随机过程分析时，模型参数采用经荷载试验分析所得数据，动力可靠性分析以该桥有限元模型为基础，采用《PMDK动力可靠度分析程序》计算。有限元模型共划分276个单元，277个节点。为验证程序模态分析的可靠性，与ANSYS结果进行对比表明，两者结果完全一致。该桥振型及自振频率见表2，计算获得结构不同位置限制位移的动力可靠度，见图5。由图5看出，对双侧界限以位移为限制条件下，大桥动力可靠度与位移方向有关;大桥不同位置动力可靠度变化趋势也不同。且挠度(UY)方向动力可靠度略高于转动(ROTZ)方向。由图5(a)看出，在相同位移限制条件下，大桥中跨跨中的动力可靠度高于边跨跨中，与整体相同;图5(b)看出，相同位移限制条件下，除两边跨跨中几点外(此几点动力可靠度不同于整体与其位移方向突变有关)，大桥动力可靠度基本一致。

采用《PMDK动力可靠度分析程序》，设大桥阻尼从0变化到1.0，计算分析得结构不同位置在限制位移条件下动力可靠度见图6、图7。

由图6看出，限制位移条件下，边跨UY动力可靠度增加幅度大于中跨，越靠近边跨支点，增加幅度越大;此规律也适用于ROTZ动力可靠度;由图7看出，大桥UY动力可靠度与阻尼比呈正相关关系，随阻尼比的增大，边跨跨中及内支点左UY动力可靠度与阻尼比近似成二次抛物线关系，中跨跨中则成明显对数关系;ROTZ动力可靠度与阻尼比间关系较复杂，内支点近似成四次抛物线关系，边跨跨中及中跨跨中则成六次抛物线关系，除个别点外，随阻尼比的增大，动力可靠度逐渐减小。

图5 大桥动力可靠度结果示意图Fig.5 Results of dynamic reliability for the bridge

图6 大桥不同位置的动力可靠度 ξb=0.0 ～1.0Fig.6 Dynamic reliability for the bridge with ξb=0.0 ～1.0 at different parts

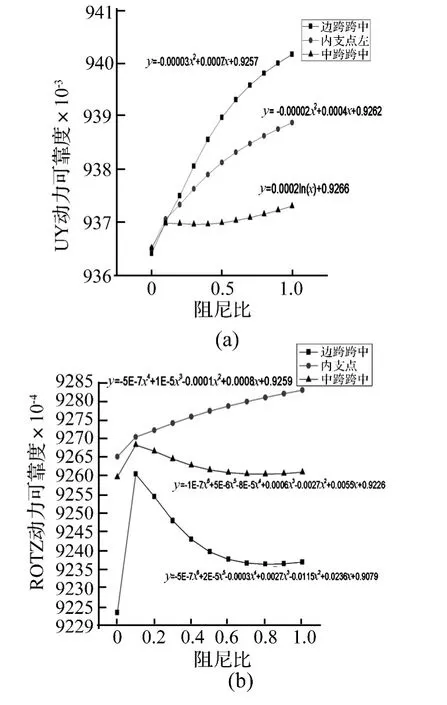
图7 大桥关键截面动力可靠度 ξb=0.0 ～1.0Fig.7 Dynamic reliability of the bridge’s key section with ξb=0.0 ～1.0

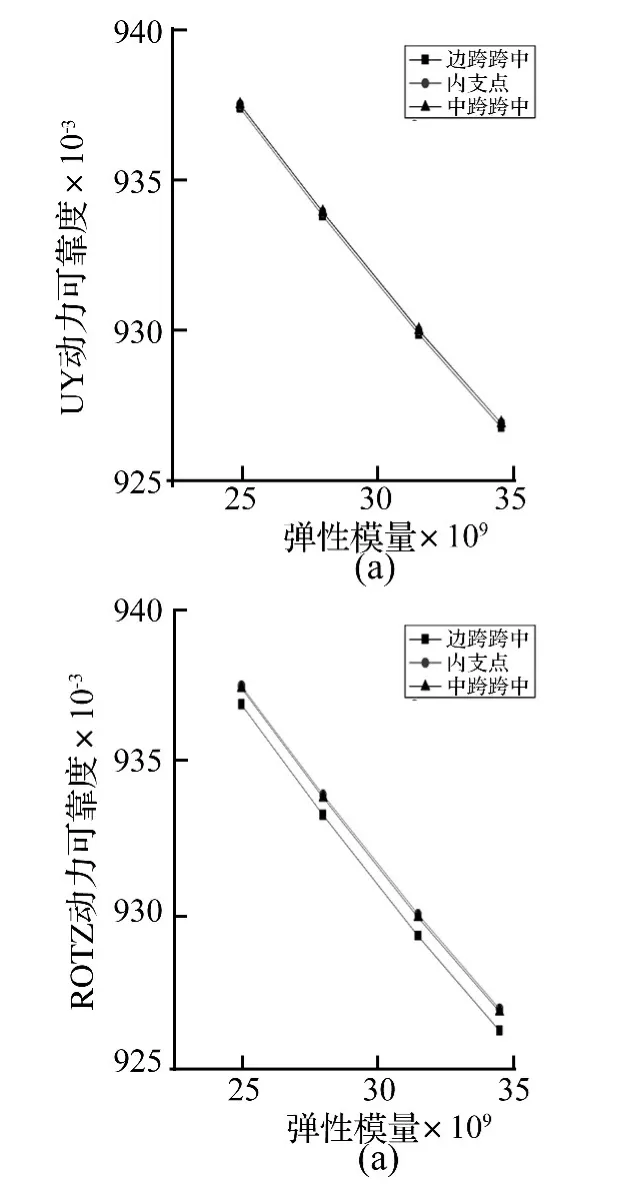
图8 大桥弹性模量对关键截面的动力可靠度Fig.8 Influences of elastic modulus on dynamic reliability of the bridge’s key section

图9 大桥不同位置动力可靠度 T=1.0 ～1000 Fig.9 Dynamic reliability for the bridge with T=1.0 ～1000 at different parts

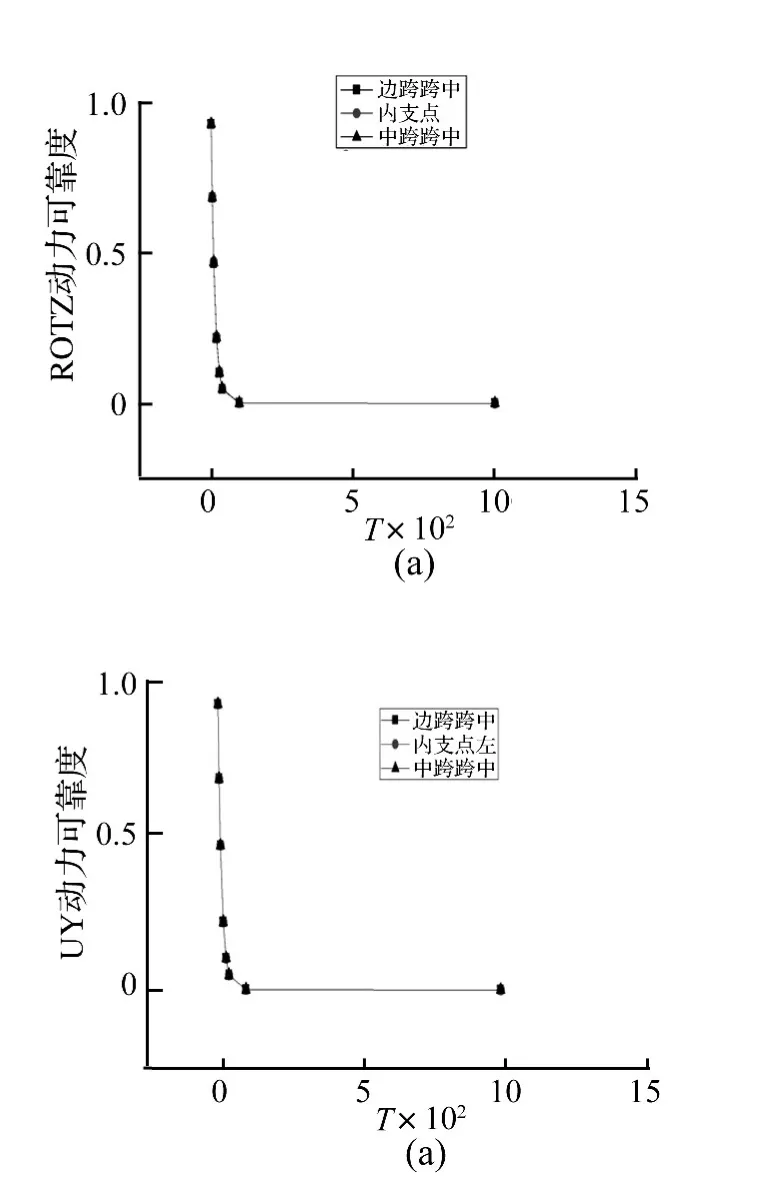
图10 大桥关键截面动力可靠度 T=1.0～1000 Fig.10 Dynamic reliability of the bridge’s key section with T=1.0 ～1000

大桥材料弹性模量对结构可靠度影响较小，随弹性模量的增大，大桥动力可靠度逐渐减小，见图8。

随时间的增加，大桥动力可靠度明显下降，见图9、图10。由计算知，T=5时，大桥动力可靠度下降26.17%，T=10时，大桥动力可靠度下降49.48%，T=100时，大桥动力可靠度接近于0。结构单侧可靠度与双侧可靠度相差较小。

4 蒙特卡罗法分析

蒙特卡罗法(Monte Carlo)为具有独特风格的数值计算方法，广泛用于求解随机性不确定性问题。随模拟次数的增加，该法计算结果会逐渐趋近精确解。因此在结构可靠度计算中被认为准精确方法，而其它近似方法精度亦常用该法验证。蒙特卡罗法分析主要过程为:

(1)随机变量取样。设xi为已知分布特征的随机变量，对可靠度分析中所遇正态分布、对数正态分布与极值Ⅰ型分布表达式为:

正态分布:

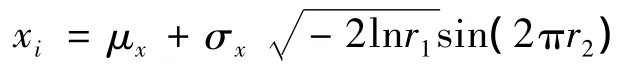
对数正态分布:

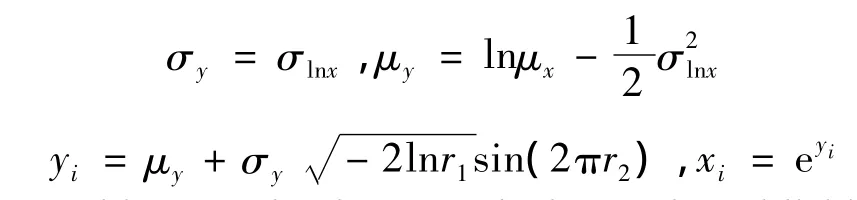
极值Ⅰ型分布:

其中:μx，σx分别为随机变量均值、标准差，r1，r2为［0，1］上相互独立均匀分布随机数。

(2)结构失效概率计算。据理论分析，要使计算达到一定精度，需满足N≥4/(Pfε2)(Pf为预估计结构失效概率，ε为相对误差)。本文选择N=1000 000，即达到10-4精度。

将随机数转换成相应数据，代入ANSYS有限元程序求解，结果表明，采用《PMDK动力可靠度分析程序》所得计算结果在10-4精度范围内完全准确，部分计算结果见表3、表4，亦验证程序的可靠性。

表3 弹性模量变化UY动力可靠度计算结果Tab.3 Results of UY dynamic reliability with modulus of elasticity variation

表4 弹性模量变化ROTZ动力可靠度计算结果Tab.4 Results of ROTZ dynamic reliability with modulus of elasticity variation

5 结论

本文基于多自由度体系随机过程分析振型分解法，推导出结构动力可靠度分析的相关参数计算公式，

用Fortran语言自编《PMDK动力可靠度分析程序》，并用蒙特卡罗法验证自编程序的可靠性。结论如下:

(1)采用无约束规划求解方法，推导出车辆荷载概率分布模型参数求解方法。并结合具体观测数据，获得概率模型。

(2)结合某旧桥静动载试验，采用参数分析获得动力可靠度计算的相关数据，用《PMDK动力可靠度分析程序》计算该桥在实际车辆荷载作用下的可靠度，结果表明，动力可靠度与位移、不同截面位置有关，跨中动力可靠度高于边跨;阻尼和弹性模量变化对大跨动力可靠度的影响为阻尼比增大，动力可靠度减小;而弹性模量变化影响可忽略。

(3)时间变化对大桥可靠度影响较大，时间越长，大桥动力可靠度下降越明显;而结构单侧及双侧可靠度相差较小。

(4)用ANSYS有限元程序求解结果与用自编程序计算结果均在10-4精度范围内，表明自编程序计算完全准确。

因沿桥梁轴线方向设有活动支座，沿轴向位移远大于挠度方向位移，故本文未考虑沿桥梁轴线方向动力可靠度。

［1］许峰炜.简支板梁桥车桥振动的横向分布特性研究［D］.杭州:浙江大学，2006.

［2］JTG D60-2004，公路桥涵设计通用规范［S］.北京:人民交通出版社.

［3］马 麟，韩万水，刘健新，等.考虑激励随机过程性的桥面行车安全可靠度分析［J］.振动与冲击，2012，31(7):112-117.

MA Lin，HAN Wan-shui，LIU Jian-xin，et al.Reliability analysis for driving safety of a vehicle on a long-span bridge considering stochastic progress characteristics of excitation［J］.Journal of Vibration and Shock，2012，31(7):112-117.

［4］郭 彤，李爱群，赵大亮.用于公路桥梁可靠性评估的车辆荷载多峰分布概率模型［J］.东南大学学报(自然科学版)，2008，38(5):763-766.

GUO Tong，LI Ai-qun，ZHAO Da-liang.Multiple-peaked probabilistic vehicle load model for highway bridge reliability assessment［J］.Journal of Southeast University(Natural Science Edition)，2008，38(5):763-766.

［5］卢 伟，强士中，李晓渝.斜拉桥抖振动力可靠性分析［J］.振动与冲击，2001，20(2):82-85.

LU Wei，QIANG Shi-zhong，LI Xiao-yu.Dynamic reliability analysis for buffeting of cable-stayed bridge［J］.Journal of Vibration and Shock，2001，20(2):82-85.

［6］Prenninger P H W，Matsumoto M，Shiraishi N，et al.Reliability of bridge structures under wind loading:consideration of uncertainties of wind load parameters［J］.Journal of Wind Engineering and Industrial Aerodynamics，1990，33(1-2):385-394.

［7］Scanlan R H.The action of flexible bridges under wind，Ⅱ:buffeting theory［J］.Journal of Sound and Vibration，1978，60(2):201-211.

［8］Bucher C G，Lin Y K，Asce F.Stochastic stability of bridges considering coupled medes［J］. Journal of Engineering Mechanics，1988，114(12):2055-2071.

［9］Deodatis G.Shinozuka M.Simulation of seismic ground motion using stochastic waves［J］.Journal of Engineering Mechanics，1989，115(12):2723-2737.

［10］Zhang L L，Li J，Peng Y B.Dynamic response and reliability analysis of tall buildings subject to wind loading［J］.Journal of Wind Engineering and Industrial Aerodynamics，2008，96(1):25-40.

［11］李振宇，余建星，田 佳，等.大跨度新型桥梁地震动力可靠度分析［J］.天津大学学报，2010，43(3):234-238.

LI Zhen-yu， YU Jian-xing， TIAN Jia， et al. Dynamic reliability analysis of large-span new-pattern bridge under earthquake［J］.Journal of TianJin University，2010，43(3):234-238.

［12］Rahlnan M S，Ei Zahaby K M.Probabilistic liquefaction risk analysis including fuzzy variables［J］.Soil Dynamics and Earthquake Engineering，1997，16(1):63-79.