基于改进HHT分析车轮椭圆化对高速列车时频特征的影响

陈双喜，林建辉

(西南交通大学 牵引动力国家重点实验室，成都 610031)

铁路系统广泛存在［1］的车轮圆周非圆化现象会引起车辆轨道系统振动响应变化，影响列车运行稳定性及安全性［2-3］。非圆化短波激励会导致轮轨力增大、横向蛇形运动、轮轨磨损加剧、滚动噪声增大。一旦车辆出现蛇形失稳，将致轮轨间强烈相互作用，加速轮轨磨损与疲劳，损坏轨道系统，甚至引发脱轨危险。Nielsen等［1-2］对车轮周期性非圆化进行过总结。Johansson等［3］通过试验分析过不同类型车轮非圆化产生原因。张雪珊等［8］研究过车轮椭圆化对列车横向稳定性影响。但止今对车轮非圆化引起车辆系统时频分布及能量分布研究较少。车辆振动响应时频分布不仅一定程度上反映悬挂刚度变化或车轮缺陷，且是确定控制反馈力的主要依据。因此在运行周期内对车辆系统进行时频分析十分必要。由于轮轨接触几何关系、轮轨接触蠕滑力、悬挂刚度及阻尼的非线性等因素［4-5］存在，车辆轨道耦合系统振动即为非线性、非平稳随机过程。常用分析方法主要为以傅里叶变换为基础的谱分析［5-6］。在分析线性、平稳信号时，傅里叶变换具良好性能;但在分析非线性、非平稳信号时，傅里叶变换则在整个时间轴积分平均，无法反映非平稳信号的时变特性。基于经验模态分解(EMD)的希尔伯特-黄变换作为分析非线性、非平稳信号方法，吸取了小波变换多分辨率优势，克服了基函数选取困难，具有良好的局部适应性，且不受Heisenberg测不准原理制约，时间及频率可同时达到高精度。该方法已用于车辆系统动力学研究，并取得良好效果［7］。本文计算车轮椭圆化激励下车辆系统动力响应，并运用改进的希尔伯特-黄变换计算分析车轮椭圆化对高速列车时频、能量分布影响。

1 车轮非圆化

车轮非圆化分为局部非圆化与全周非圆化［8］。局部非圆化主要表现为扁疤、剥离及其它形式波长局部非圆化，由制动热损伤及滚动接触疲劳引起。全周非圆化主要是车轮多边化，包括:车轮磨损(或加工)导致的偏心，椭圆化，三角形化，四边形化，如图1所示。形成、发展机理尚未知。多数情况下，前三种非圆化起主导作用。本文以二阶非圆化为例，研究车轮椭圆化对车辆系统时频、能量分布影响。

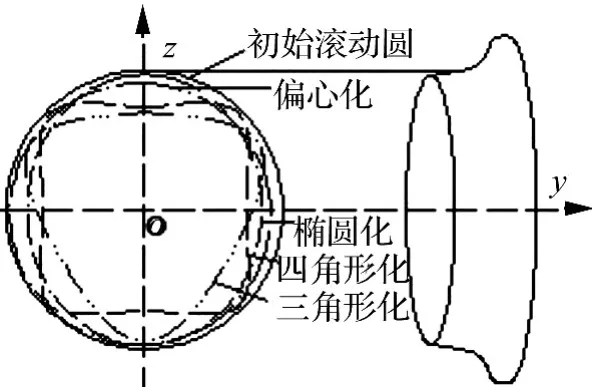
图1 车轮全周非圆化Fig.1 Periodic out-of-round wheel

2 车辆/轨道耦合动力学模型

车辆轨道耦合动力学模型包括车辆模型、轮轨耦合模型、轨道模型(图2)。车辆模型包括轮对、转向架、车体、一系悬挂、二系悬挂、减振器、抗蛇形减振器、横向止挡等。整个车辆系统振动响应微分方程见文献［9］。轨道模型选取我国广泛应用、具优越减振降噪性能的弹性支承块式无砟轨道。考虑计算规模、精度、计算成本，忽略钢轨的剪切变形、转动惯量影响，采用欧拉梁模型及文献［9］钢轨振动微分方程。弹性支承块无砟轨道垂向刚度主要由扣件及块下胶垫提供，横向刚度由支承块橡胶套靴提供［10］。轮轨之间采用赫兹非线性接触理论与沈志云-Hedrick-Elkins理论实现车辆系统与轨道系统耦合［9］。车辆轨道系统振动可能由车轮缺陷或轨道不平顺引起。本文考虑轨道不平顺为谐波不平顺。车轮缺陷为车轮椭圆化，其数学模型用椭圆极坐标(图3)方程表示为:

式中:r(t)为车轮表面至圆心距离;a，b分别为椭圆车轮长、短半轴长度，θ(t)为名义接触半径与水平轴夹角。定义椭圆度为长短半轴长度之差，相位差为左右轮θ(t)之差。若相位差为零，则采用轨道高低不平顺模拟;若相位差不为零，则采用轨道扭曲不平顺模拟［8］。对该大型复杂非线性动力学微分方程组，只能采用直接数值积分法。本文采用新型快速显式积分［9］求解。

3 改进希尔伯－黄变换

希尔伯特-黄变换包括经验模态分解及希尔伯特变换。经验模式分解(EMD)由Huang［11］提出。将信号s(t)自适应分解为多个本征函数IMF(ci)及一个余项r(t)，从而反映信号内部特点。即:

图2 车辆轨道耦合系统Fig.2 Model of vehicle-track coupling system

图3 车轮椭圆化模型Fig.3 Model of wheels ovalization

为使瞬时频率有意义，本征函数(IMF)须满足两条件:① 在整个数据序列中，极值点数量与过零点数量相等，或最多相差一个;② 在任一时间点上，信号局部极大值确定的上包络线与局部极小值确定的下包络线均值为零。由于具有自适应分解特性，对非平稳、非线性信号处理效率较高。本文采用改进的EMD方案:以极值域均值模式分解方法(EMMD)［12］提高局部均值求解精度，减少计算量;用波形匹配法［13］与极值点对称延拓相互配合抑制端点效应;用能量波动法［14］限制分解次数、识别虚假IMF分量，计算能量分布。能量波动法中能量比例ζi为各IMF分量与原始信号比值:

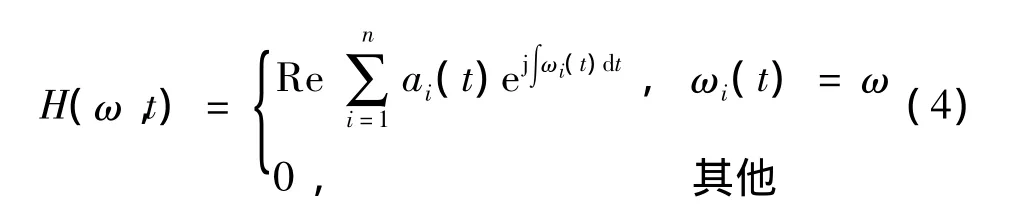
式中:频率ωi(t)与幅值ai(t)是时间的变量，可构成时间、频率、幅值三维时频幅值谱图H(ω，t)。对式(4)时频幅值谱图进行积分得信号边缘幅值谱:

式中:T为序列时间长度。边缘谱表征数据在每个频率点的累积幅值分布，基函数是自适应的IMF函数组。由此可消除傅里叶变换的虚假谐波分量，使信号频谱更清晰真实［11］。

4 计算结果与比较

对车辆轨道耦合模型进行求解可得系统动力学响应。车辆模型及参数采用国产某和谐号动车组。本文假设轨道谐波不平顺波长10 m，波深5 mm，列车运行速度300 km/h，计算长度100 m。运用改进的希尔伯特-黄变换对响应进行分析，即可得耦合系统动态特征。

计算表明，车轮椭圆度小于0.5 mm，轮轨未脱离接触，傅里叶变换与希尔伯特-黄变换结果一致;椭圆度大于0.5 mm，由于高频轮轨冲击存在，两者差异较大。车轮椭圆度1 mm、2 mm时车体垂向振动加速度傅里叶谱见图4。由图4看出，椭圆度1 mm时车体振动主频为8.3 Hz、62 Hz;椭圆度2 mm时，由于轮轨脱离接触造成强烈轮轨冲击，傅里叶谱主频分布在8.3 Hz、62 Hz及其倍频处(虚假谐波分量)。椭圆度为1 mm、2 mm时车体垂向振动加速度时频分布见图5。由图5看出，椭圆度1 mm时，车体垂向振动存在两个主要分量:8.3 Hz附近的平稳振动(谐波不平顺波长10 m)与55～65 Hz范围内波动的频率调制振动(椭圆化波长为轮周长一半，约1.35 m);椭圆度2 mm时，轮轨存在高频冲击，车体振动能量除8.3 Hz附近，亦在100 Hz以内广泛分布，即发生能量扩散。对时频谱积分所得希尔伯特边缘谱见图6，与图4相比傅里叶谱反映的振动情况更真实。

运用能量波动法计算振动分量能量比例，结果表明，椭圆度1 mm时，椭圆化引起的振动占转向架、车体垂向振动总能量的90%、41%，不平顺引起的振动占转向架、车体垂向振动总能量的10%、56%;椭圆度2 mm时，椭圆化引起的振动占车体垂向振动总能量的20%，不平顺引起的振动占转向架、车体垂向振动总能量的14%、32%。由此可见，椭圆度过大(2 mm)，轮轨冲击造成车体能量扩散频域更广。

图4 车体垂向振动傅里叶谱Fig.4 Fourier spectrum for vertical acceleration of car body

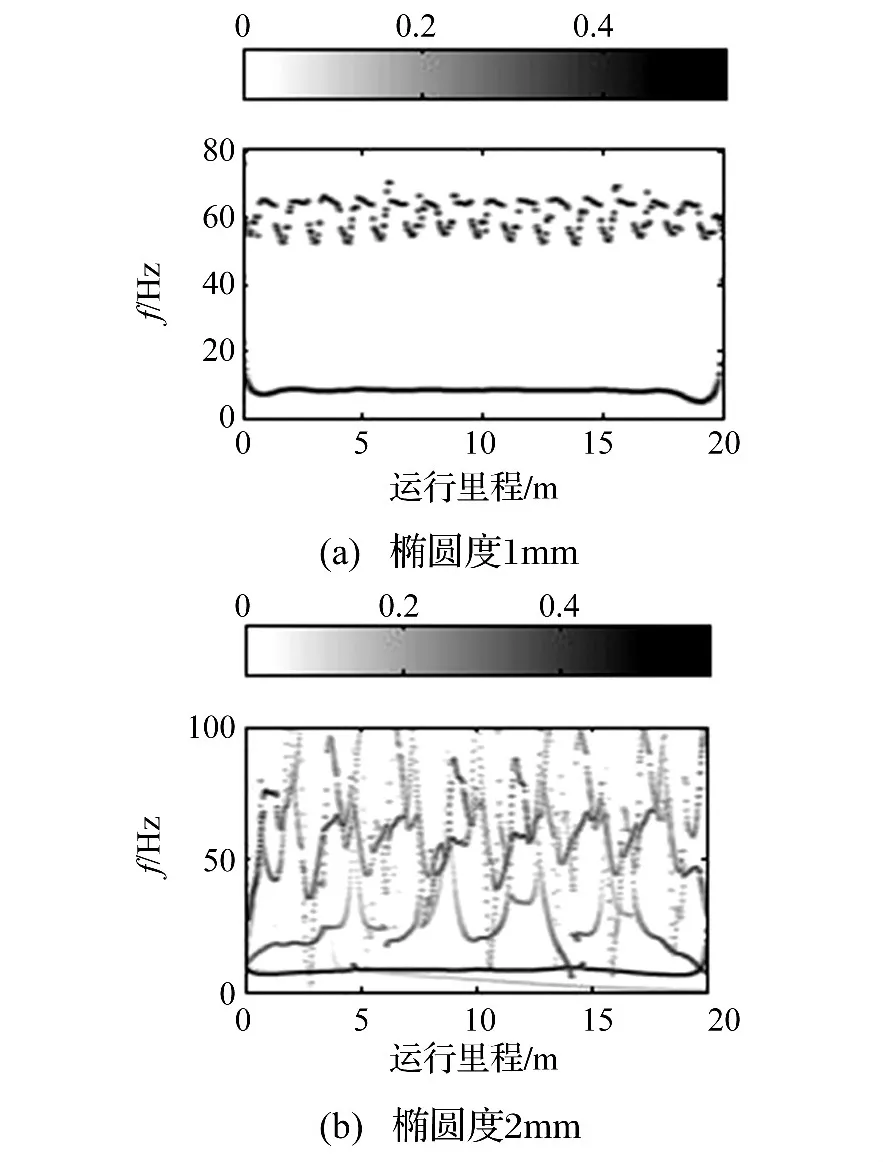
图5 车体垂向振动时频幅值谱Fig.5 Hilbert spectrum for vertical acceleration of car body

车轮椭圆化相位差同样对车辆系统振动产生明显影响。考虑第一、二轮对存在椭圆化，但仅第一轮对存在相位差。计算表明，相位差小于π/2，轮对偏向轨道一侧蛇形运动，从π/2到π，轮对在轨道另一侧蛇形运动，与文献［8］结果一致。由于对称，只考虑π/2范围内相位差。在椭圆度1 mm、不同相位差情况下，转向架横向振动加速度高频分量时频分布见图7，频率调制信号在中心频率62 Hz附近波动，且椭圆化相位差越小，波动范围越宽。转向架横向振动加速度边缘谱见图8，相位差为π/2时带宽最窄，能量最集中，相位差越小带宽越大，能量分布越宽。

图6 车体垂向振动边缘谱Fig.6 Marginal spectrum for vertical acceleration of car body

椭圆化相位差亦会对转向架及车体垂向、侧滚、摇头、点头运动动态特征造成影响。限于篇幅，略去时频分布图。计算表明，转向架垂向、侧滚、摇头、点头加速度高频分量在60±20 Hz范围内分布，带宽受相位差影响较小。车体垂向、点头加速度高频分量亦为频率调制信号，波动范围在60±10 Hz，带宽受相位差影响较小。车体侧滚加速度高频分量带宽随相位差增大而减小。车体摇头加速度数量级很小，可忽略。

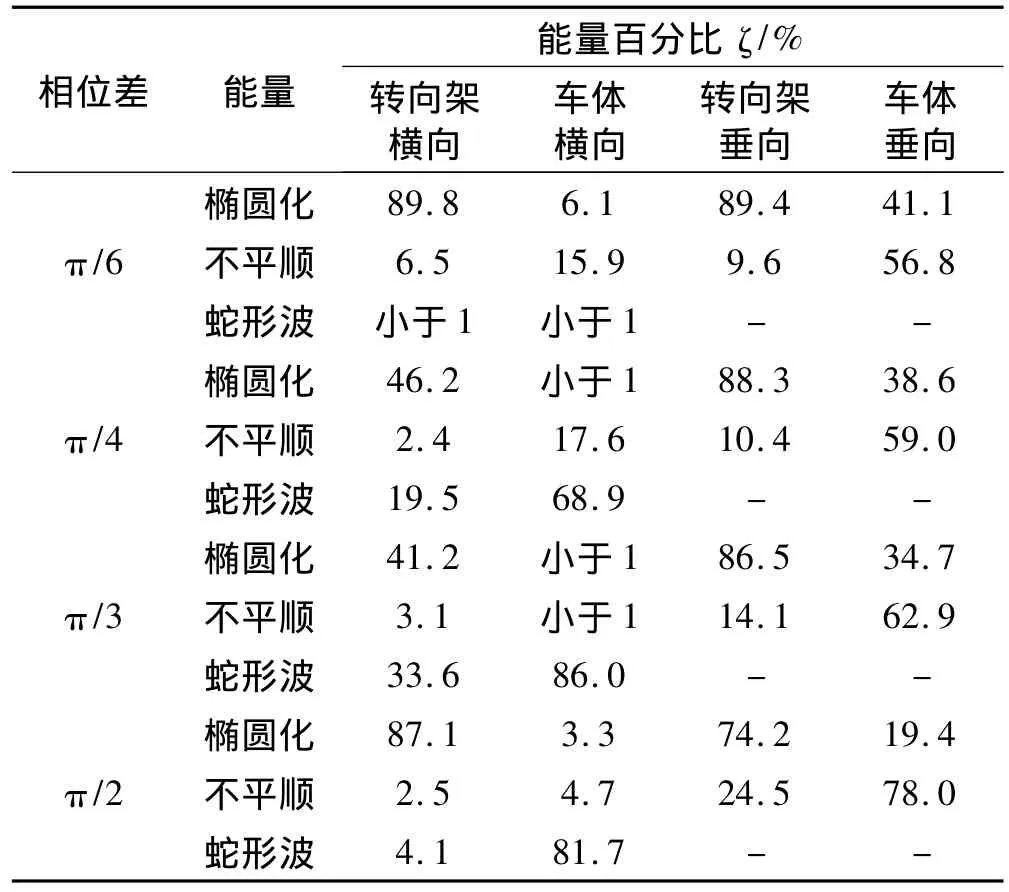
表1 车辆系统振动能量分布Tab.1 Energy distribution of vehicle system

车轮椭圆化相位差也能造成车辆系统振动能量分布差异，通过能量波动法分析，得转向架及车体能量比例分布情况见表1。由表1看出，相位差越大，椭圆化引起转向架、车体垂向振动能量比例越小、不平顺引起振动能量比例越大。相位差对车辆系统横向振动影响较复杂，造成的车体横向波长蛇形运动见如图9。相位差为π/6、π/2时椭圆化引起转向架振动能量比例最大，相位差为π/3时蛇形引起转向架、车体振动能量比例最大。椭圆化能量在转向架振动能量中所占比例远大于车体中比例。

图7 转向架横向振动时频幅值谱Fig.7 Hilbert spectrum for Lateral acceleration of bogie

计算表明，车轮椭圆化相位差也对车体侧滚及点头造成较大影响，对车体摇头影响较小。相位差从π/6到π/2，椭圆化引起能量占车体侧滚总能量的95% ～99%，即相位差影响不大;相位差从π/6到π/2，椭圆化引起振动能量占车体点头总能量的35%、32%、29%、16%，影响程度不断减小;而不平顺引起振动能量占车体点头总能量的65%、67%、71%、83%，影响程度不断增大。

图8 转向架横向振动时频幅值谱Fig.8 Marginal spectrum for lateral acceleration of bogie

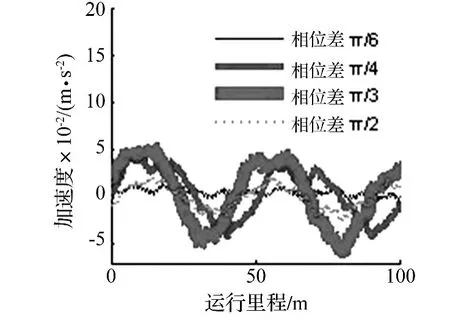
图9 车体横向振动加速度Fig.9 Lateral acceleration of car body

5 结论

改进的希尔伯特-黄变换能有效提取车辆轨道耦合系统的时频、能量分布。车轮椭圆度超过一定范围会导致轮轨强烈高频冲击，振动响应频率调制及带宽变化可使振动能量频域扩散更广。椭圆化相位差不但会造成转向架及车体垂向、横向、侧滚、点头、摇头振动分量的频率调制及带宽变化与能量分布差异，亦会造成车辆系统蛇形运动及蛇形能量差异，且对转向架能量分布影响大于车体。

［1］Nielsen J C O，Johansson A.Out-of-round railway wheels-a literature survey［J］.IMechE Journal of Rail and Rapid Transit.，2000，214(F):79-91.

［2］Barks D W，Chiu W K.A review of the effects of out-of-round wheels on track and vehicle components［J］.IMechE Journal of Rail and Rapid Transit，2005，219(F):151-175.

［3］Johansson A. Out-of-round railway wheels-causes and consequences，an investigation including field tests，out-ofroundness measurements and numerical simulations［D］.GBteborg:Chalmers University of Technology，2005.

［4］Shen Z Y，Hedrick J K，Elkins J A.A comparison of alternative creep force models for railway vehicle dynamic analysis［C］.Proc.of 8th IAVSD Symposium， MIT，Cambridge，1983:591-605.

［5］陈 果.车辆-轨道耦合系统随机振动分析［D］.成都:西南交通大学，2000.

［6］晋智斌.车-线-桥耦合系统及车-桥随机振动分析［D］.成都:西南交通大学，2007.

［7］Chen S X，Lin J H，Chen J Z.Time-frequency analysis of vehicle/bridge coupling system based on Hilbert-Huang transform-influence of wheel tread reprofiling［C］.Proceedings of The 2nd International conference on Artificial Intelligence，Management Science and Electronic Commerce，Zhengzhou，China，2011:6052-6055.

［8］张雪珊，肖新标，金雪松.高速车轮椭圆化问题及其车辆稳定性的影响［J］.机械工程学报，2008，44(3):50-55.

ZHANG Xue-shan，XIAO Xin-biao，JIN Xue-song.Influence of high speed railway wheels ovalization on vehicle stability［J］.Chinese Journal of Mechanical Engineering，2008，44(3):50-56.

［9］翟婉明.车辆轨道耦合动力学［M］.北京:中国铁道出版社，1997.

［10］陈小平，王 平，陈 嵘.弹性支承块式无砟轨道的减振机理［J］.铁道学报，2007，29(5):69-72.

CHEN Xiao-ping， WANG ping， CHEN Rong. Damping vibration mechanism of the elastic bearing block track［J］.Journal of the China Railway Society，2007，29(5):69-72.

［11］Huanu N E.Shen Z，Long S R，et al.The empirical mode decomposition and the hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proc Royal Society London A，1998，454(1971):903-995.

［12］盖 强.局域波时频分析方法的理论研究与应用［D］.大连:大连理工大学，2001.

［13］邵晨曦，王 剑，范金锋，等.一种自适应的EMD端点延拓方法［J］.电子学报，2007，35(10):1944-1946.

SHAO Chen-xi，WANG Jian，FAN Jin-feng，et al.A selfadaptive method dealing with the end issue of EMD ［J］.Acta Electronica Sinica，2007，35(10):1944-1949.

［14］李 辉，王 瀚，白 亮，等.改进希尔伯特-黄变换方法提取水轮机动态特征信息［J］.中国电机工程学报，2011，31(2):78-83.

LIHui， WANG Han， BAILiang， etal， Dynamic characteristic information extraction of hydro-turbine based on improved Hilbert-Huang transform method［J］.Proceedings of the Chinese Society for Electrical Engineering，2011，31(2):78-83.