基于全局控制网的三维形貌测量方法

崔晓川 邾继贵 隆昌宇

天津大学精密测试技术及仪器国家重点实验室，天津，300072

0 引言

近年来，高精度测量大尺寸物体三维形貌［1］的研究引起了人们的高度重视，其中，双目立体视觉装置结合激光扫描装置构成的传感器被广泛应用于三维形貌测量中。但是，由于受到传感器视场范围［2］的制约，对大尺寸物体的测量往往不能一次完成，而是需要将被测物体分割成若干相关联的区域进行分别成像测量，最终通过特定方法把各个相关的区域拼接［3］成一个整体，进而实现大尺寸三维形貌的测量。目前使用的拼接方法主要有序列拼接方法和整体拼接方法。因为序列拼接方法会产生较大的累积拼接误差，所以在精度要求较高、分割区域较多的情况下序列拼接方法实用性较差。相比而言，利用全局控制点建立全局控制网的拼接方法不会产生累积的拼接误差，该拼接方法主要基于视差原理以及平差算法［4］获得全局控制点在各测站中的三维坐标，再通过不同测站中的同名控制点将数据融合，进而得到全局控制网，最后利用双目立体视觉装置结合激光扫描装置［5］将每次测量的传感器坐标系下的三维坐标映射到全局控制网中，完成大尺寸物体的三维形貌测量。

经纬仪测量系统是较早应用于大尺寸测量领域的分布式测量系统之一，然而使用经纬仪测量系统进行测量之前，需要进行人工互瞄等比较复杂繁琐的工作，效率较低，人为误差明显，重复精度比较低，不利于大批量连续作业。另外，经纬仪整个系统的便携性往往较差［6］。本文提出一种基于全局控制网的三维形貌测量方法，该方法具有自标定功能，测量时所有被测控制点采用图像处理技术通过计算机系统获得亚像素级的测量精度，无需人为识别，并且最终系统的便携性较好。该方法的图像处理操作能够实现计算机全自动化，故测量速度快，且光束平差算法的精度高，从而保证了该方法具有较高的精度。

1 测量方法概述

基于全局控制网的三维形貌测量方法首先需要在被测物体表面均匀且无规则地放置少量编码点［7］和较多的非编码点［8］用以构建全局控制网，这些编码点和非编码点统称为全局控制点。利用大视场相机在不同区域对被测物体以及全局控制点成像。通常假设第一个测站坐标系为全局坐标系，在全局控制点精确配准的基础上利用光束平差技术获得全局控制点在各测站中的三维坐标，然后再将不同测站中的全局控制点融合到全局坐标系中进行联合平差，得到全局控制点精确的全局三维坐标，进而建立起全局控制网；利用非接触测量传感器，根据双目视觉测量原理对大尺寸被测物体进行局部测量，利用每次成像视场中至少3个全局控制点获得测量传感器坐标系到全局控制网坐标系的转换关系，将局部的形貌信息拼接到全局控制网中，实现大尺寸物体的三维形貌测量（图1）。

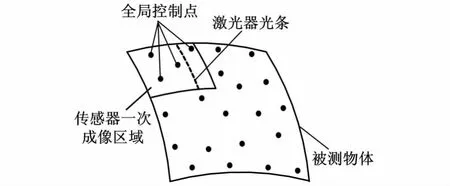
图1 测量拼接示意图

2 建立全局控制网

全局控制网就是利用特殊反射材料制成的由编码点和非编码点构成的能够反映被测物体三维形貌信息的点状网格。其中编码点有各自独立的特征（即编码值），容易实现同名匹配；而非编码点没有独立的特征，必须通过特定的方法找到不同图像中同名的非编码点，才能实现非编码点的匹配。

在大尺寸三维形貌测量过程中，相机的视场范围相对于尺寸较大的被测物体而言往往很小，因此对大尺寸物体三维形貌的测量往往不能一次性完成。于是，就不可避免地需要先对大尺寸物体进行分区域的局部测量，然后再将测量结果拼接起来。目前使用较为广泛的序列拼接方法是将每个区域的测量结果拼接到与该区域有重叠部分的相邻区域，进而构成一个新的较大区域；重复上述操作最终将每个区域均与第一个区域实现拼接。当被测物体尺寸很大、分割的区域很多时，后续区域的测量结果需要经过多次的旋转、平移转换运算才能得到在最初区域坐标系下的测量坐标。由于每进行一次旋转、平移转换运算就会产生一定的误差，那么进行多次转换运算后必定会产生相当大的累积误差，从而大大影响测量精度。

而基于全局控制网的大尺寸三维形貌测量方法则可以大幅地减小由多次转换运算而引起的测量误差。该方法是在全局控制网建立的基础上，通过全局控制点获得每次测量时传感器坐标系与全局控制网坐标系的转换关系。这样只需计算一次旋转、平移转换关系就可以将每次测量的结果拼接到全局控制网中，进而实现大尺寸三维形貌的测量。由此可见，该方法既简化了测量过程又有效地提高了测量精度。

2.1 全局控制网建立流程

首先根据对极几何约束［2，4］关系，通过求得的基本矩阵来实现非编码点的匹配。得到同名的非编码点后，根据光束交汇原理［4］，利用光束平差技术就可以精确算出全局控制点在各个测站坐标系下的三维坐标。再通过至少3个相同编码点确定各个测站的转换关系，然后就可以将所有的全局控制点的三维坐标统一起来，最后利用全局坐标系下所有点的坐标值进行联合平差求得所有全局控制点的精确坐标，从而建立起一个全局控制网。全局控制网建立流程如图2所示。

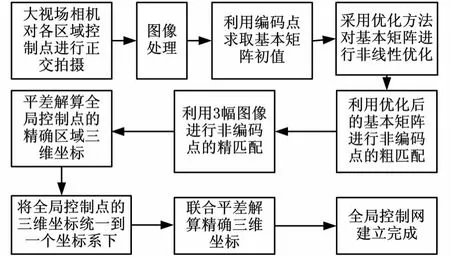
图2 全局控制网建立流程图

（1）在被测物体表面均匀且无规则地放置全局控制点（包括编码点和非编码点），利用大视场相机，分别对被测物体的每个区域进行拍摄测量，测量每个区域时需要选取两个位置分别进行正交拍摄，并且要保证拍摄时尽量使所需的全局控制点分布在相机的视场中心，这样可以尽可能地消除由相机镜头的畸变而引起的测量误差。

（2）对每个区域的4幅图像均采用直方图处理、二值化滤波、质心提取等图像处理方法［4］进行处理，得到包含清晰特征的全局控制点的测量图像；通过辨别编码点的编码值实现4幅图像中编码点的同名匹配；对于每2幅图像构成的图像对，利用至少8个同名编码点结合测量图像中编码点的图像坐标求取基本矩阵。因为八点法求得的基本矩阵存在很大的误差，而且此误差可能导致后续的非编码点的匹配产生错误，最终使得全局控制网建立失败，所以需要采用匹配点到各自对应极线距离平方和最小的非线性优化方法对基本矩阵进行优化。优化过程中将八点法求得的基本矩阵作为初值进行迭代；用优化后的基本矩阵结合对极几何约束关系对相应的图像对中的非编码点进行初步粗匹配；为了提高匹配的正确率，还需要利用3幅图像进行非编码点的精确匹配，匹配后对非编码点进行全局编号。

（3）得到精确匹配的非编码点后，利用非编码点在4幅图像中的图像坐标，采用光束平差算法，求得全局控制点在每个测站中的精确三维坐标；为了使每个区域中所有的全局控制点的坐标实现统一，需要利用每两个测站中公共的编码点在各自测站坐标系下的三维坐标计算出这两个区域的坐标系转换关系，即旋转、平移矩阵；最终通过所有区域的旋转、平移矩阵将所有的全局控制点的坐标统一到全局坐标系中；选取一定的距离阈值，将全局坐标系中相互距离小于阈值的控制点融合为一个点，大于阈值的控制点作为新点加到全局控制网中，最后进行总体的联合平差运算得到全局控制点精确的全局三维坐标，从而实现全局控制网的精确建立。

（4）使用双目视觉测量传感器并结合激光扫描装置，对被测物体表面的各个区域进行双目视觉测量；利用传感器视场中至少3个全局控制点得到传感器测量坐标系到全局控制网坐标系的旋转、平移转换关系，进而将测得的被测区域信息拼接到全局控制网中，实现大尺寸物体的三维形貌测量。

2.2 全局控制网建立的基本原理

2.2.1 确定基本矩阵

对极几何约束关系在两幅图像的非编码点匹配过程中有着重要的作用。其原理如图3所示。

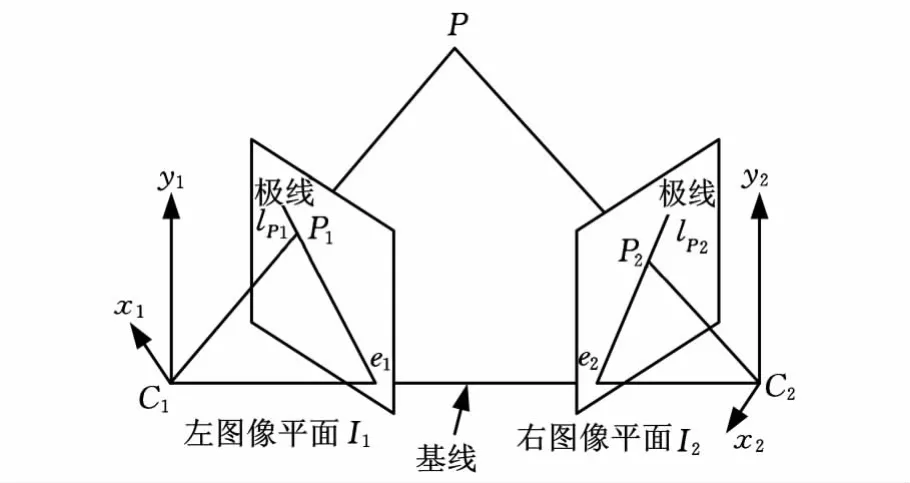
图3 对极几何约束关系示意图

两相机中心C1和C2的连线分别交左右图像平面于极点e1和e2，全局控制点P在左右两幅图像中的像点为P1和P2，e1与P1的连线lP1称为P2在左图像中的极线，e2与P2的连线lP2称为P1在右图像中的极线。对极线间存在一定的几何关系，其关系式可以表达为［2］

其中，m表示某幅图像中的一个像点，m′代表其余图像中对应的匹配像点。

基于式（1）求得的基本矩阵F存在一定的误差，需要对求得的基本矩阵F进行优化处理。优化方法是用式（1）得到的基本矩阵F作为迭代初值，利用非线性优化方法得到更精确的基本矩阵F，优化式为［2］

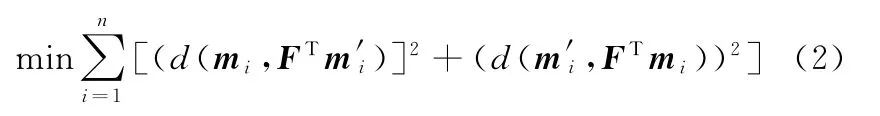
其中，d（mi，FTm′i）表示对应匹配像点的极线距离。

2.2.2 全局控制点匹配

通过选取一定的距离阈值得到优化后的基本矩阵之后，首先利用2幅图像根据对极几何约束求得一幅图像中非编码点在另一幅图像中对应的极线，选取一个误差带，把误差带内的疑似匹配点作为粗匹配的结果记录下来；再利用3幅图像对非编码点进行精确匹配，如图4所示。设空间中一个非编码点M 在3幅图像中成的像点分别为m1、m2、m3，图像1中的像点m1在图像2中的对应极线为l1，且在误差带h1中的点均为m1在图像2中的疑似匹配点；同理，m1在图像3中对应的极线为l3，且在误差带h3中的点也均为m1在图像3中的疑似匹配点；图像3中的疑似匹配点在图像2中也有各自对应的极线l2和误差带h2。则图像2中误差带h1与误差带h2公共部分中包含的非编码点即为m1在图像2中精确匹配的同名非编码点。利用这种方法得到所有图像中精确匹配的非编码点。

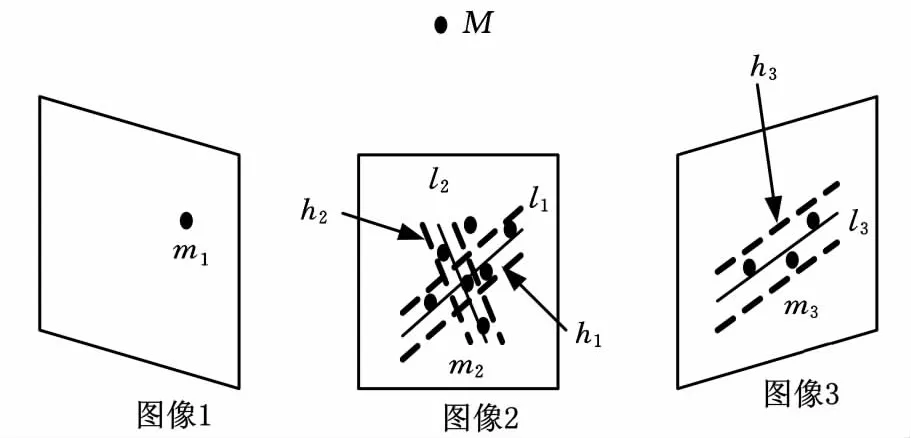
图4 优化基本矩阵后非编码点的精确匹配

2.2.3 光束交汇原理与平差技术

非编码点正确匹配后，就要求得每个全局控制点的三维坐标值。双目立体视觉原理表明，三维空间中的一个点在两个相机像面中所成的像点分别与对应相机中心的连线一定在空间中交于一点（图5），此即光束交汇原理。该原理也正是光束平差算法的基础。

对于单个相机而言，由几何比例关系可以得到下面的公式［2］：

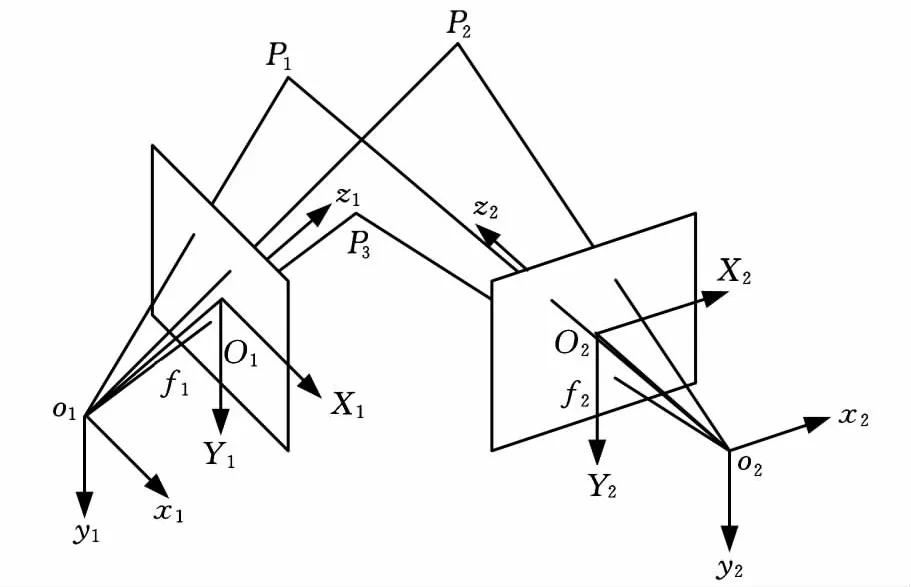
图5 光线交汇原理图示

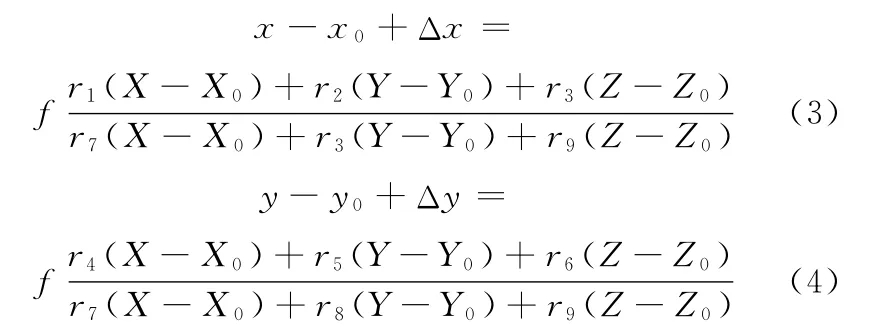
式中，（x，y）为空间点在像平面的成像坐标；（x0，y0）为像面中心坐标；（Δx，Δy）为系统误差修正值；f为相机焦距；（X，Y，Z）为空间点在全局坐标系下的坐标；（X0，Y0，Z0）为相机主点在全局坐标系下的坐标。

r1、r2、……、r9构成相机坐标系到全局坐标系的旋转矩阵。其中，Δx和Δy分别满足如下关系［2］：

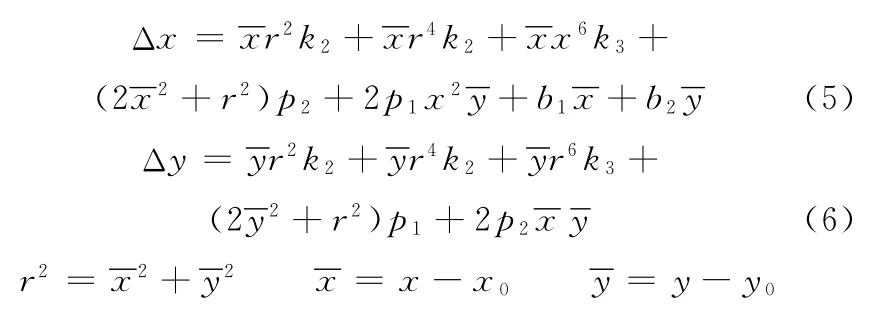
式中，k1、k2、k3、p1、p2、b1、b2为相机参数。

平差解算时引入观测值改正数vx、vy和近似值改正数dx、dy，则式（3）、式（4）变形为［2］

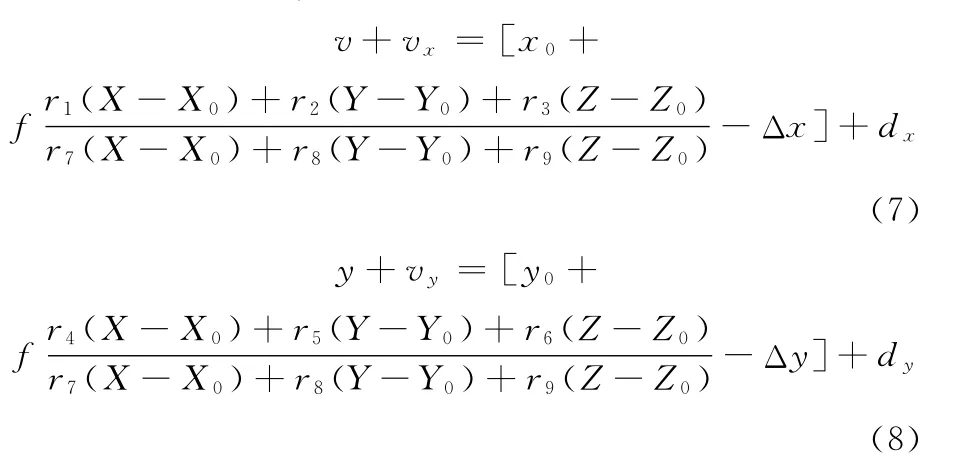
全局控制点在所有测站下均满足上述关系式，故可将所有测站下的全局控制点列出的方程构成一个大规模的方程组，且空间中一个全局控制点在n幅图像中的像点应满足［2］：

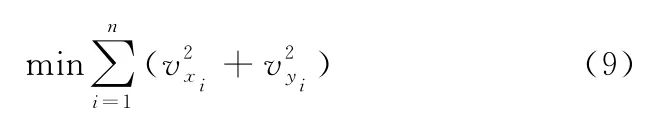
采用光束平差技术可以求解上述大规模方程组，即把相机的内外参数以及控制点的全局坐标均视为未知量整体，通过求方程组的优化方法求出未知量。

平差解算时需要有合适的平差初值，以使迭代运算收敛于最优解。平差初值包括各测站坐标系相对于全局坐标系的转换关系初值以及控制点全局三维坐标初值。其中坐标系转换关系初值可以通过基本矩阵分解求得两个测站之间的旋转、平移转换关系，而全局三维坐标初值可以利用分解得到的旋转、平移矩阵结合各像面坐标计算得到。获得平差初值后，就可以通过多次迭代计算出全局控制点在该区域精确的三维坐标。将不同区域中相同的全局控制点融合起来后，再利用光束平差技术进行联合平差运算就可以得到所有全局控制点精确的全局三维坐标。

3 实验

使用 Kodak dcspro14n摄像机和 Nikon24mm镜头结合计算机系统对白车身的车盖（图6）进行三维形貌测量，对均匀且无规则地分布在车盖上的全局控制点进行拍摄。实验时，只需按照上述方法拍摄相应的车盖图像，其余处理操作无需人工参与，整个过程能够实现全自动化，因此该测量方法速度快。最终融合得到的全局控制点如图7所示，得到的实验数据如表1所示，其中距离真值是利用V－stars系统测量得到的。

图6 测量实物

图7 拼接融合后的结果

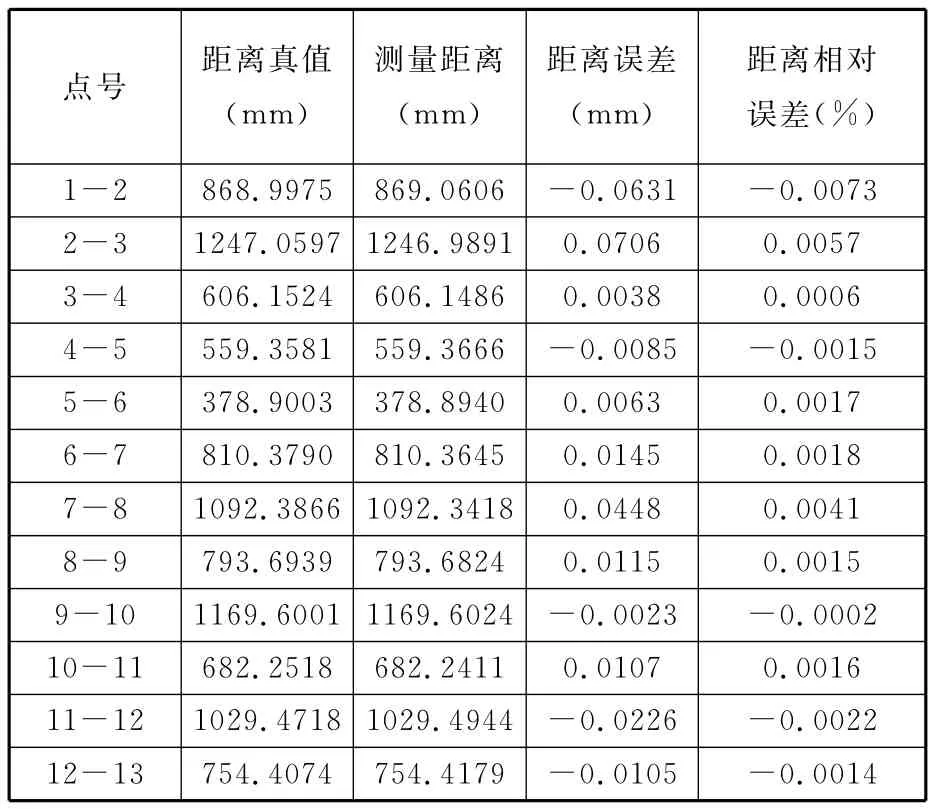
表1 实验数据比对

由表1数据可知：距离误差绝对值的平均值为0.0224，上述距离误差的均方差为0.0226。

4 结论

由实验数据可知，本文方法的测量精度（相对误差）可以在0.01%以内，且测量计算过程完全自动化。由此可见，基于全局控制网的大尺寸三维形貌测量方法能够高精度地恢复被测物体三维形貌特征。该方法有效地提高了测量时的拼接精度，同时使测量变得更加快速简单。

［1］Rosin P L.Shape－Measuring the Orientability of Shapes［J］.Lecture Notes in Computer Science，2007，4673：620－627.

［2］张广军.机器视觉［M］.北京：科学出版社，2005.

［3］Chaneski W.Simplifying Measurement of Complex Shapes［J］.Modern Machine Shop，1998，71（2）：48－49.

［4］邾继贵，于之靖.视觉测量原理与方法［M］.北京：机械工业出版社，2011.

［5］叶声华，邾继贵，张滋黎，等.大空间坐标尺寸测量研究的现状与发展［J］.计量学报，2008，29（增刊1）：1－6.Ye Shenghua，Zhu Jigui，Zhang Zili，et al.Status and Development of Large－scale Coordinate Measurement Research［J］.Acta Metrologica Sinica，2008，29（S1）：1－6.

［6］周虎.基于视觉的目标跟踪与空间坐标定位系统研究［D］.天津：天津大学，2011.

［7］郑建冬，张丽艳，周玲，等.基于单数码相机自由拍摄的空间点定位［J］.航空学报，2007，28：1521－1526.Zheng Jiandong，Zhang Liyan，Zhou Ling，et al.3D Target Location with One Single Hand－held CCD Camera［J］.Acta Aeronautica et Astronautica Sinica，2007，28：1521－1526.

［8］张谦，陈安.一种嵌入式机器视觉的图像处理系统设计［J］.广东第二师范学院学报，2011，31（5）：85－90.Zhang Qian，Chen An.An Embedded Image Process System Design of Machine Vision［J］.Journal of Guangdong Education Institute，2011，31（5）：85－90.